基于改進支持向量機的致密砂巖儲層參數預測研究

摘" 要： 致密砂巖儲層的評價技術既是油氣勘探開發的重點，也是難點。目前對致密砂巖儲層的儲層參數的預測與評價，依然采用傳統的儲層參數預測方法，結合測井曲線進行建模，用以對滲透率、孔隙度等參數進行擬合，主要運用的方法有經驗公式、回歸分析等，其中大部分方法都是基于線性的，無法反映致密儲層特有的沉積和成巖作用所導致的非均質性強的特點，無法揭示致密儲層中測井曲線與儲層參數之間的復雜非線性關系。針對此問題，提出在傳統儲層參數預測模型的基礎上，對測井曲線與儲層參數的非線性關系進行分析，挖掘更多現有測井信息，進行支持向量機儲層參數預測模型的建構，并采用粒子群算法、頭腦風暴算法、布谷鳥算法等三種支持向量機的改進優化算法對模型參數進行測試，篩選出最優的儲層參數預測模型。將該模型應用于研究區儲層參數預測評價中，有效提高了預測評價精度，為致密儲層精細預測評價和非常規油氣田的高效開發提供了有力的技術保障。

關鍵詞： 儲層參數； 致密砂巖； 測井曲線； 機器學習； 支持向量機； 粒子群算法

中圖分類號： TN911.1?34" " " " " " " " " " " " "文獻標識碼： A" " " " " " " " " " " " 文章編號： 1004?373X（2024）05?0132?07

Research on tight sandstone reservoir parameter prediction

based on improved support vector machine

XU Yingjin1， PANG Zhenyu2

（1. School of Information Engineering， East China University of Technology， Nanchang 330013， China;

2. Jiangxi Engineering Technology Research Center of Nuclear Geoscience Data Science and System， East China University of Technology， Nanchang 330013， China）

Abstract： The evaluation technology of tight sandstone reservoir is not only the focus but also the difficulty of oil and gas exploration and development. At present， the traditional methods are still adopted in the prediction and evaluation of reservoir parameters of tight sandstone reservoir. In these methods， the modeling is carried out in combination with the well logging curves， so as to fit parameters such as permeability and porosity. The main methods used are empirical formulas and regression analysis. Most of these methods are based on linearity， which fails to reflect the strong heterogeneity caused by the unique sedimentation and diagenesis of tight reservoirs and fails to reveal the complex nonlinear relationship between well logging curves and reservoir parameters in tight reservoirs. In view of the above， on the basis of the traditional reservoir parameter prediction model， the nonlinear relationship between well logging curves and reservoir parameters is analyzed and the existing well logging information is more fully explored to construct a reservoir parameter prediction model based on support vector machine （SVM）. The model parameters are tested with three improved optimization algorithms of SVM， including particle swarm optimization （PSO）， brainstorming algorithm and cuckoo search （CS） algorithm， so as to select the optimal reservoir parameter prediction model. The model improves the accuracy of prediction and evaluation effectively when it is applied to the prediction and evaluation of the parameters of the reservoir in the study area. Therefore， the proposed model can provide strong technical support for fine prediction and evaluation of tight reservoirs and efficient development of unconventional oil and gas fields.

Keyword： reservoir parameter; tight sandstone; well logging curve; machine learning; SVM; PSO algorithm

0" 引" 言

近年來，隨著能源需求的增長，石油勘探開發進入了一個新的高峰期，致密砂巖油氣資源逐漸成為勘探開發的主戰場。在致密砂巖儲層復雜的地質條件下，如何更準確地預測儲層參數是提高石油勘探開發效率和效益的關鍵之一。致密砂巖儲層參數的復雜性和不確定性使得傳統的統計學和機器學習方法難以準確預測儲層參數。

在傳統和現代的預測方法中，常見的方法包括回歸分析、人工神經網絡、決策樹等[1]。這些方法需要先對數據進行前期處理，提取出相關的特征變量，并進行建模和預測。然而，對于復雜的地質條件和多變的儲層參數，這些方法往往需要耗費大量的時間和算力成本來處理數據，且預測精度和穩定性也難以同時得到保證。這些方法的局限性在于，需要大量的樣本數據來訓練模型，對數據的質量和分布敏感，對于復雜的非線性問題難以進行處理[2?5]。此外，傳統方法還存在著對地質知識的依賴性較強，對于新的儲層參數預測往往需要重新構建模型[6?8]。這些弊端導致傳統方法在預測致密砂巖儲層參數時的不足，難以滿足實際工程需要。

SVM是一種能夠從大規模數據中自動提取特征并進行高級別抽象的機器學習技術[9?10]。近年來，SVM技術也逐漸應用于地球物理勘探領域，如地震數據處理、巖石分類和儲層預測等[11?14]，其具有無需地質和測井曲線知識、不需要大量采樣數據、不需要繁瑣的參數調整，同時能夠全面考慮多特征，實現更高精度的測井曲線與儲層參數預測等優點。然而，在致密砂巖儲層參數預測領域，SVM改進算法的應用仍然相對較少。

因此，本文以延長油田杏子川采油廠化子坪區長6儲層為例，開展基于改進支持向量機致密砂巖儲層參數的預測方法研究，充分揭示致密砂巖儲層內的非線性關系，提高儲層參數預測的精度，為石油勘探開發提供一種新的預測方法，為SVM改進算法技術在地球物理勘探領域的應用提供一定的參考和借鑒。

1" 傳統儲層參數預測方法

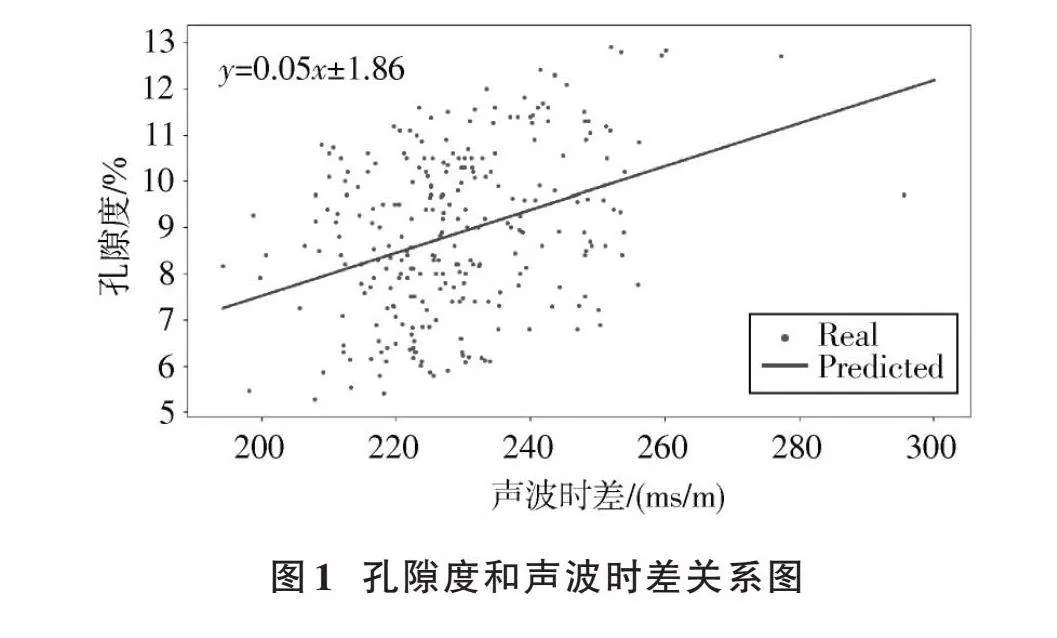
孔隙度是反映儲層物性的重要參數，孔隙度的大小是度量儲層存儲能力的重要指標，對于測井解釋及儲層評價具有重要意義。聲波時差（AC）、密度（DEN）、補償中子（CN）都可用來計算地層孔隙度。目前，延長油田杏子川采油廠化子坪區長6儲層的儲層參數預測采用的是傳統的線性回歸法，即利用巖心分析孔隙度與聲波測井曲線之間的關系，通過統計回歸分析建立了孔隙度測井解釋模型。然而，延長油田杏子川采油廠化子坪區長6儲層屬于典型的致密砂巖儲層，傳統的線性回歸法不能很好地反映出致密砂巖儲層特有的非線性映射關系，導致孔隙度的預測精度不高，相關系數僅為0.432，無法滿足實際的預測需求。因此，本文引入機器學習技術，充分挖掘延長油田杏子川采油廠化子坪區長6致密砂巖儲層的非線性關系，探索建立更加適合研究區實際情況的機器學習模型。孔隙度和聲波時差關系如圖1所示。

根據模型算出其評估參數MSE與[R2]如表1所示。

2" 支持向量機回歸預測

支持向量機（Support Vector Machine， SVM）由俄羅斯統計學家Vapnik等[15?16]首先提出，旨在解決小樣本、非線性及高維度等類型下的復雜問題，可以在對問題缺乏詳細認識的情形下，對輸入的樣本經特定的非線性映射進行訓練和學習，因此在國內外的儲層參數預測方面有著廣泛的研究和應用。SVM模型的學習能力強，相比常規的預測方法，前者的優點包括：

1） 無需對地質及測井曲線知識作充分的掌握。

2） 不需要大量的油井巖石采樣數據。

3） 不需要進行繁瑣的多維度參數調整。

4） 有對多特征進行考量，能夠更加全面反映出測井曲線與儲層參數的關系，實現更高精度的預測。

在支持向量機分類問題中，最困難的部分就是找出最優超平面。為了處理離群點或噪聲數據的影響，在優化目標中平衡分類誤差和模型復雜度，獲取最佳準確率，本文構建儲層參數的支持向量機回歸預測模型時，引入了[ε]?不敏感損失函數，其數學表達式如下：

[L（y-f（x））=0，" " y-f（x）≤εy-f（x）-ε，" " y-f（x）gt;ε] （1）

式中：[y]為樣本的真實值；[f（x）]為樣本的預測值；[ε]為不敏感參數。如果[y]與[f（x）]間的誤差絕對值≤[ε]，那么可不考量此誤差；如果[y]與[f（x）]間的誤差絕對值gt;[ε]，那么需對誤差進行計算。

2.1" 非線性支持向量機回歸

研究發現，如果直接構造回歸預測函數，會使得數據處理變得非常復雜，導致模型的效率不高，于是本文使用非線性映射函數[φ（xi）]將測井曲線數據從原始空間映射到模型的特征空間里，然后把該數據轉化為線性關系，最后再構造回歸預測函數。

在非線性情況下，回歸預測函數形式如下：

[f（x）=w?φ（x）+b] （2）

式中：[w]為超平面法向量；[φ（xi）]為非線性映射函數；[b]為閾值。

在[ε]?不敏感損失函數的基礎上，可以通過引入松弛變量[（ξ）]來進一步放寬對誤差的限制，以便讓模型不斷優化參數，在引入松弛變量[（ξ）]后，則優化問題公式為：

[minw，b，ξ12w2+Ci=1mξi+ξ*i] （3）

約束條件為：

[i=1m（αi-α*i）=00≤αi，α*i≤C] （4）

式中：[C]為懲罰因子；[αi]為拉格朗日乘子；[α*i]為支持向量；[m]為樣本的最大編號。進而得出非線性回歸估計函數：

[f（x）=xi∈SV（αi-α*i）K（xi，x）+b] （5）

式中：[K（xi，xj）=φ（xi）?φ（xj）]為核函數；[SV]為標準支持向量。

能夠發現，在求解過程中，對于非線性情況需確定3個參數：[ε]、[C]和[K（xi，xj）]。這3個參數對非線性支持向量機回歸的預測精度和推廣能力影響均不相同。

2.2" 關鍵技術

支持向量機有兩項關鍵技術，現有研究主要涉及到以下兩方面：

1） 最優超平面

當訓練集的數據可以被完全分類時，不同類中最近的兩個或多個向量（支持向量）與超平面的距離最大，那么就是最優超平面。基于最小結構風險原則，本文將求最優超平面轉變為求二次函數最優解，從而設計具有最大間隔的最優超平面。

2） 非線性問題

在儲層參數預測中，大多數數據均是線性不可分的，也就是在處理測井曲線數據中是無法依靠超平面進行區分的，為使得此問題得到解決，支持向量機引入了核空間理論，也就是依靠對非線性函數的運用，實現樣本由低維空間向特定高維空間映射，進而向線性可分問題轉化，使得問題求解更加簡便，最終實現對樣本點的分隔[17]。

3" 優化的支持向量機

在支持向量機的訓練和預測中，損失函數參數[ε]和核函數的參數[σ]是核心問題，如何對以上參數的選擇進行優化是研究的熱點問題[18]，也是難點問題，傳統的網格搜索（Gird Search）在一定程度上解決了這個問題，但是需要大量的試錯實驗才能達到令人滿意的效果。為使得實驗更加高效，本研究進行了預測模型的建構，對損失函數參數、核函數參數和懲罰函數參數引入以下算法進行優化選擇，下面簡要介紹各種算法的基本原理、優化步驟等。

3.1" PSO粒子群算法

粒子群優化算法（Particle Swarm Optimization， PSO）是以進化思想為基礎的一種算法，它能夠依靠對粒子的極值與粒子群的整體最優解進行比較，不斷調整速度和位置，最后得到的單個最優極值作為整個粒子群的當前全局最優解[19]。

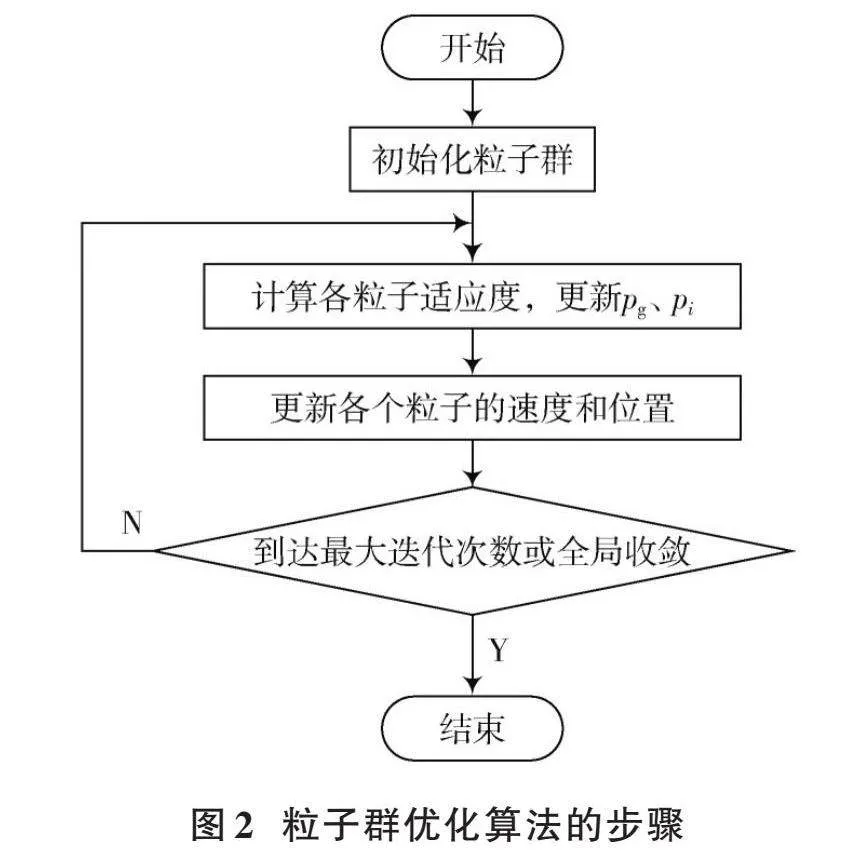
在PSO中，任一粒子均有位置和速度向量，而各個粒子在每次迭代過程中都是有規律的，各個粒子按照公式（6）來變換速度和位置，直到找到最優解為止。粒子群優化算法流程如圖2所示。

[vi+1=ωvi+c1r1（pi-xi）+c2r2（pg-xi）xi+1=xi+vi+1] （6）

式中：[v]為速度；[x]為位置；[ω]為慣性權值；[c1]和[c2]為加速系數，分別表示個體認知因子和社會經驗因子；[r1]和[r2]是隨機數，用于引入隨機性；[pi]是第[i]個粒子歷史上的最佳位置（個體最優解）；[pg]是整個粒子群歷史上的最佳位置（全局最優解）。

3.2" BSO頭腦風暴算法

頭腦風暴優化算法是由史玉回專家等[20]提出的，是一種基于蜂群智能的優化算法，其主要運用聚類思想，通過局部最優逐步實現全局最優，在尋找一種新穎前衛的思維方法時，收集連續更新的最優解，以變異算法達到算法的全局最優，適用于解決具有多個局部最優解和高維度輸入參數的問題。

3.3" CSO布谷鳥算法

布谷鳥搜索（Cuckoo Search）是基于啟發式搜索的優化算法，由劍橋大學的教授楊新社和S.戴布等[21]提出，布谷鳥尋找鳥巢下蛋的過程則類似在特定空間中尋找解，只要不被宿主鳥發現就是好的鳥巢，鳥巢的好壞直接反映解的好壞。位置更新的方式對算法的收斂速度有著一定影響，具體算法如下所示。

布谷鳥算法的邏輯如下：

1：目標函數[f（x）]，[x=x1，x2，…，xdT]

2：產生[n]個寄主的初始種群[xi]

3：while （[t]lt;MaxGeneration） or （stop criterion） do

4：隨機選取一布谷鳥

5：經Levy飛行產生一解

6：對解的質量或目標函數值[fi]進行評估

7：在[n]個巢中，隨機選擇一個（假設為[j]）

8： if" [figt;fj] then

9：用解[i]代替[j]

10：end if

11：拋棄一部分（[pa]）糟糕的巢

12：由式（1）進行計算，獲得新巢的解

13：保存最佳的解（或者高質量解的巢）

14：排列解，找出最佳

15：更新[t←t+1]

16：end while

17：總結處理與可視化

break

相關研究表明，依靠萊維飛行（Levy Flight）能夠獲取全局最優解，而不會出現局部最優解的困境，且它和布谷鳥算法能夠有效配合。

4" 優化支持向量機的模型效果

本文利用延長油田杏子川采油廠化子坪區長6儲層的原始測井曲線數據與巖心物性分析數據，對模型進行訓練、測試評估。

4.1" 數據預處理

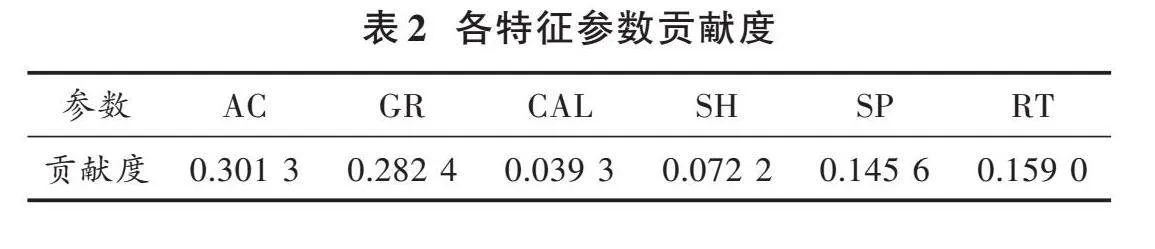
首先將屬于儲層參數的巖心分析孔隙度和滲透率作為目標數據列，根據文獻[22?24]，初選出全波聲波時差（AC）、自然伽馬（GR）、裸眼井徑（CAL）、自然電位（SP）、泥質含量（SH）、普通視電阻率（RT）作為輸入特征參數，利用主成分分析（PCA）進行降維處理，計算各個字段因子方差貢獻率，其貢獻率結果如表2所示，最終優選出因子貢獻率前四位的主成分因子：AC、GR、SP、RT作為模型的輸入特征參數。

4.2" 支持向量機模型構建及測試結果

4.2.1" 模型的構建

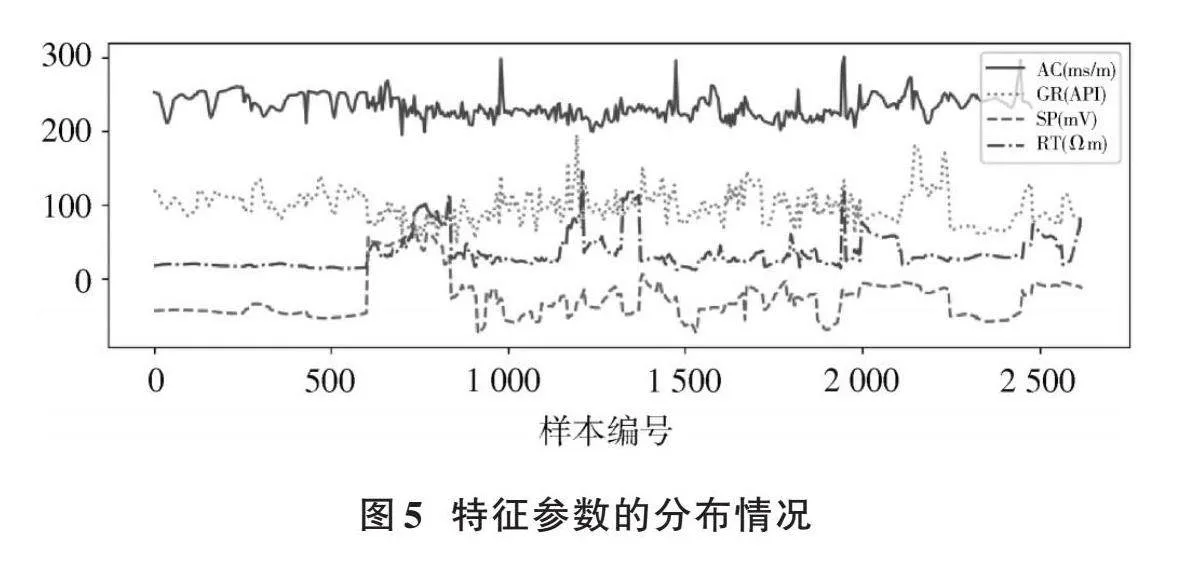
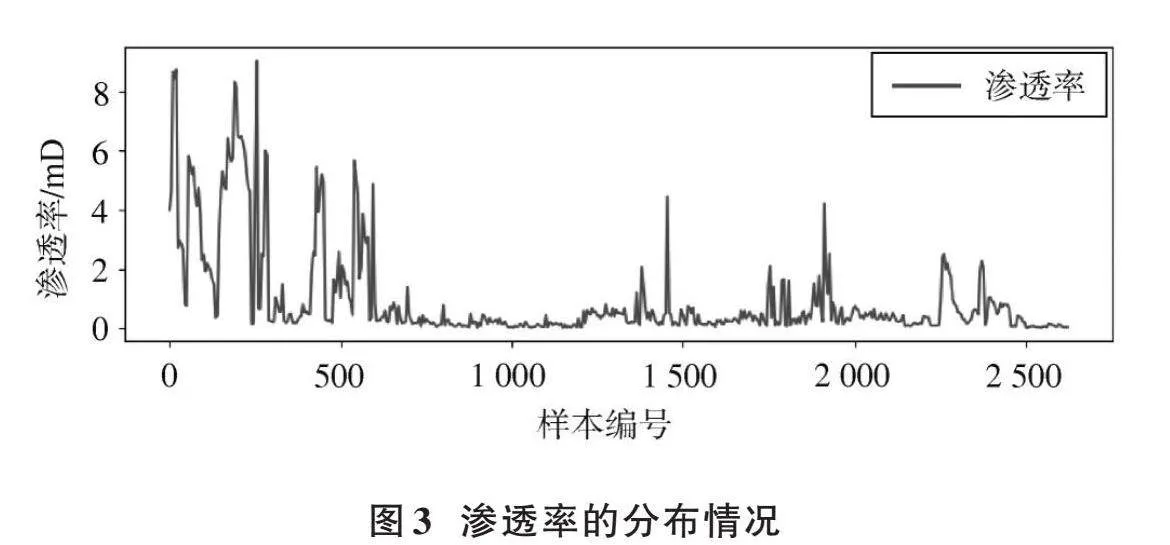
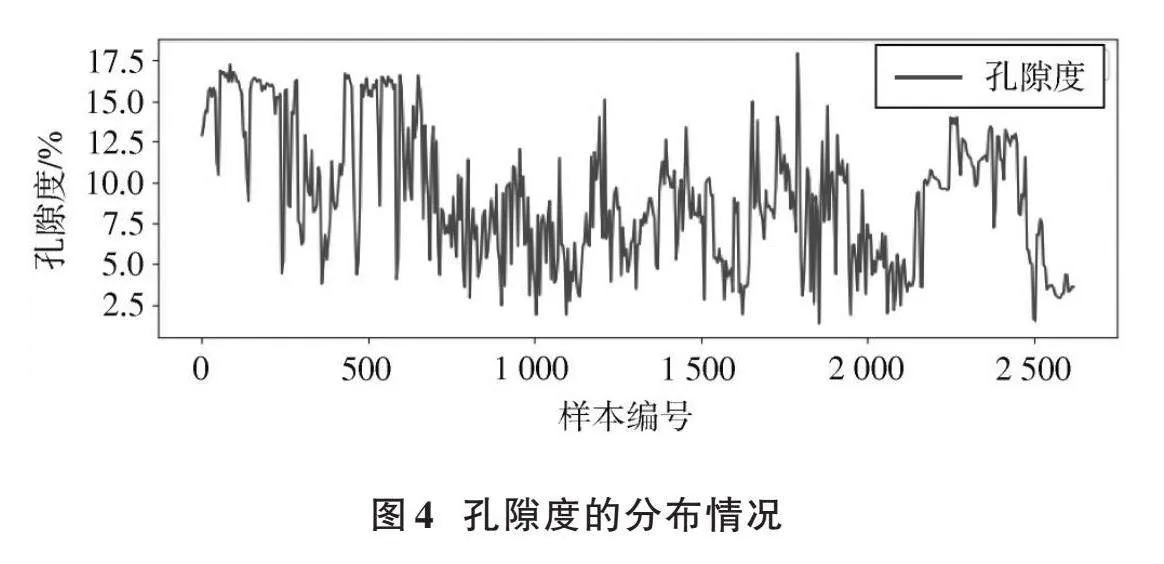
測井數據結果見圖3～圖5。

由圖3、圖4可知：相鄰樣本之間，孔隙度與滲透率的波動較大，呈現明顯非線性關系，適宜采用支持向量機的辦法對問題進行求解。

由圖5可知，輸入特征參數的分布差異較大，故本文首先對數據進行Min?Max標準化處理，將其數值轉換到0～1區間。

本文將含2 625個樣本的數據集按8∶2的比例劃分為訓練集、測試集。

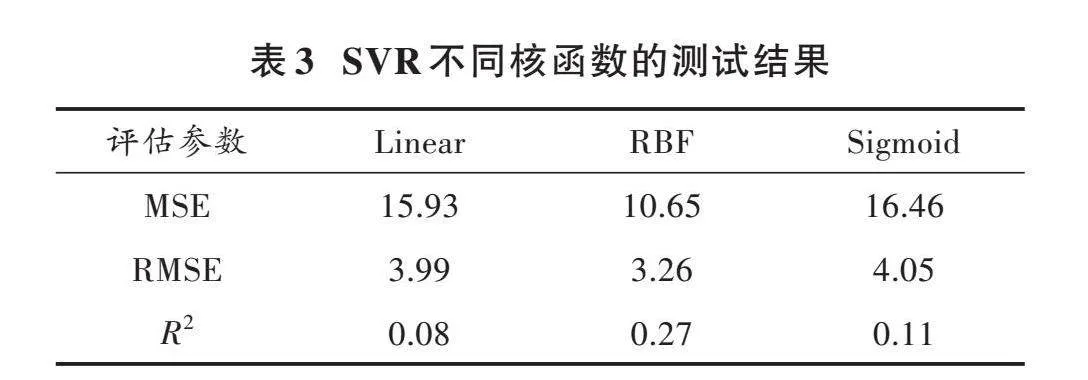
首先用相同的參數（懲罰參數[C]=500，核參數[σ]=0.01，損失函數參數[ε]=0.3）分別測試，線性核函數（Linear Kernel Function）、高斯徑向基核函數（Radial Basis Kernel Function）、Sigmoid核函數（Sigmoid Kernel Function）這三種不同核函數對輸入參數（AC、GR、SP、RT）和孔隙度進行擬合回歸，結果如表3所示（poly核函數在測試運行時，升維操作導致維度過高，在運行中出現超時的問題，故不考慮）。

結合相關文獻和表3，本文決定采用高斯徑向基核函數進行后續實驗。

4.2.2" 粒子群算法對支持向量機的參數調試

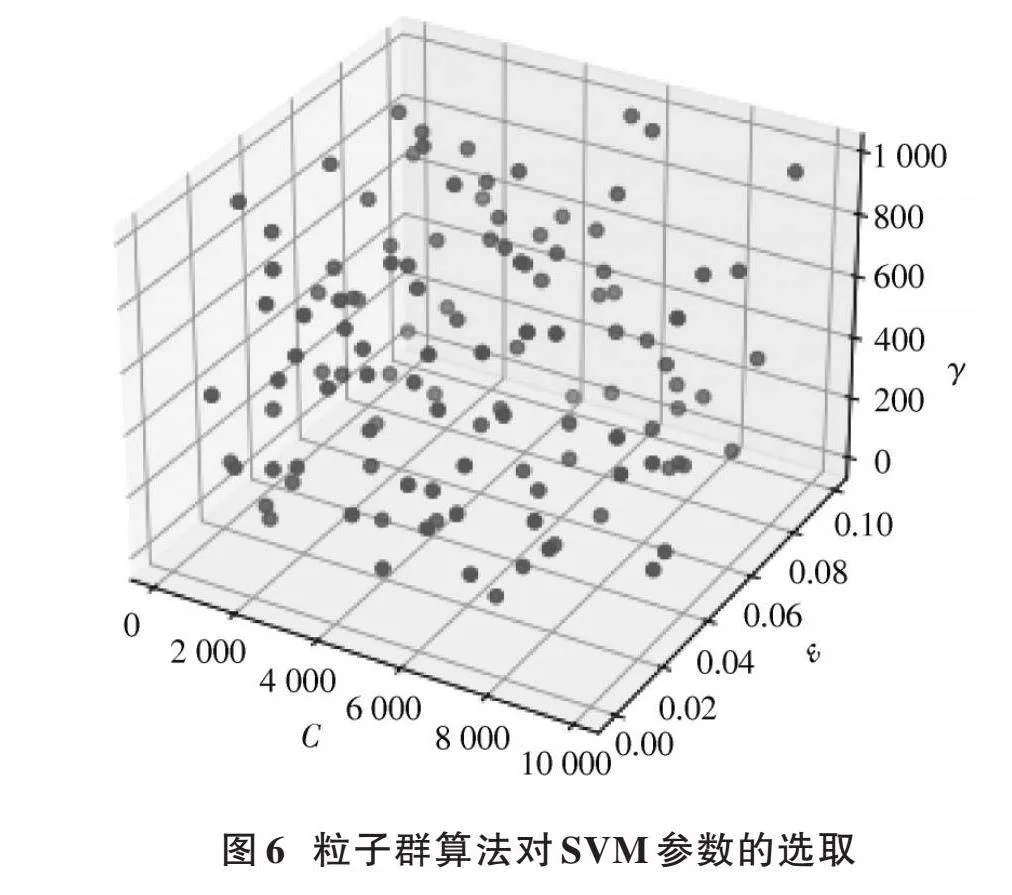
在向量機優化領域，主流優選PSO算法，以此求懲罰函數參數[C]和核函數參數[σ]，所有粒子根據粒子群的極端情況來調整其速度和位置，據此思路，本文利用PSO算法求出了長6區的SVM模型所需最優參數，如圖6所示，具體數據如下：

Best Regressor： SVR（[C]=2 528.0， degree=3， epsilon=1e-2， gamma=0.574 717 060 884 4， [ε]=0.30， kernel='rbf'， max_iter=-1， shrinking=True， tol=0.001）

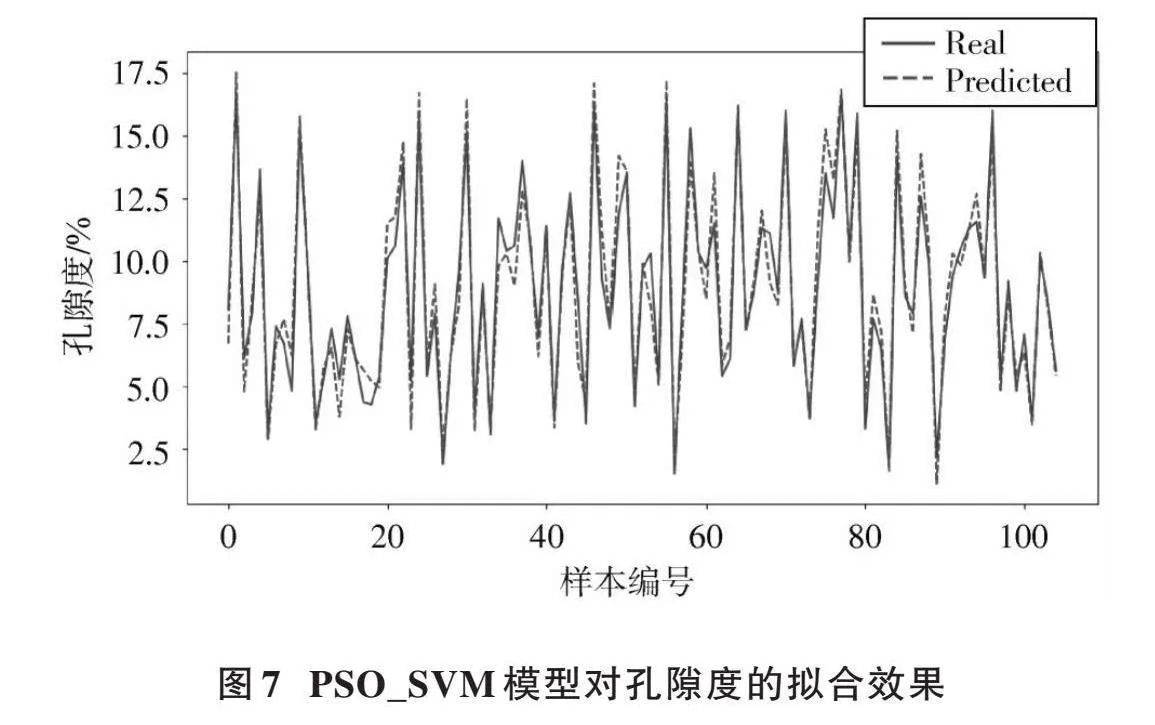
對孔隙度擬合程度如圖7所示。

根據模型算出其評估參數MSE與[R2]，如表4所示。

4.2.3" BSO頭腦風暴算法對支持向量機的參數調試

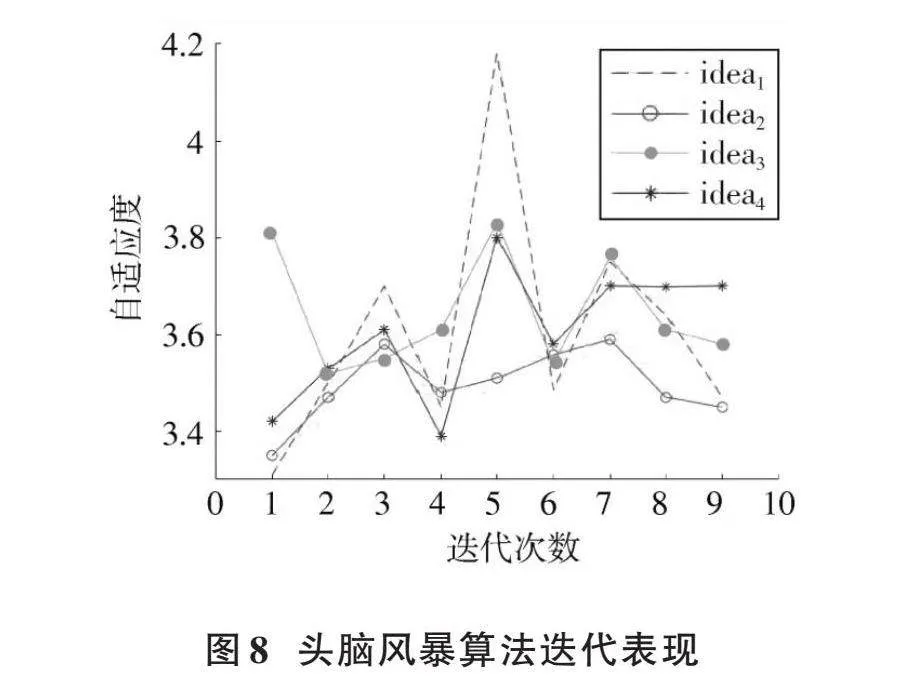
頭腦風暴算法的基本流程：通過不斷的自適應迭代更新想法（idea）進行實驗，經過調試結果如圖8所示，選出最佳的參數如下：

Best Regressor： SVR（[C]=1 559.0， degree=3， epsilon=1e-2， gamma=1.669 804 527 553 0， [ε]=0.51， kernel='rbf'， max_iter=-1， shrinking=True， tol=0.001）

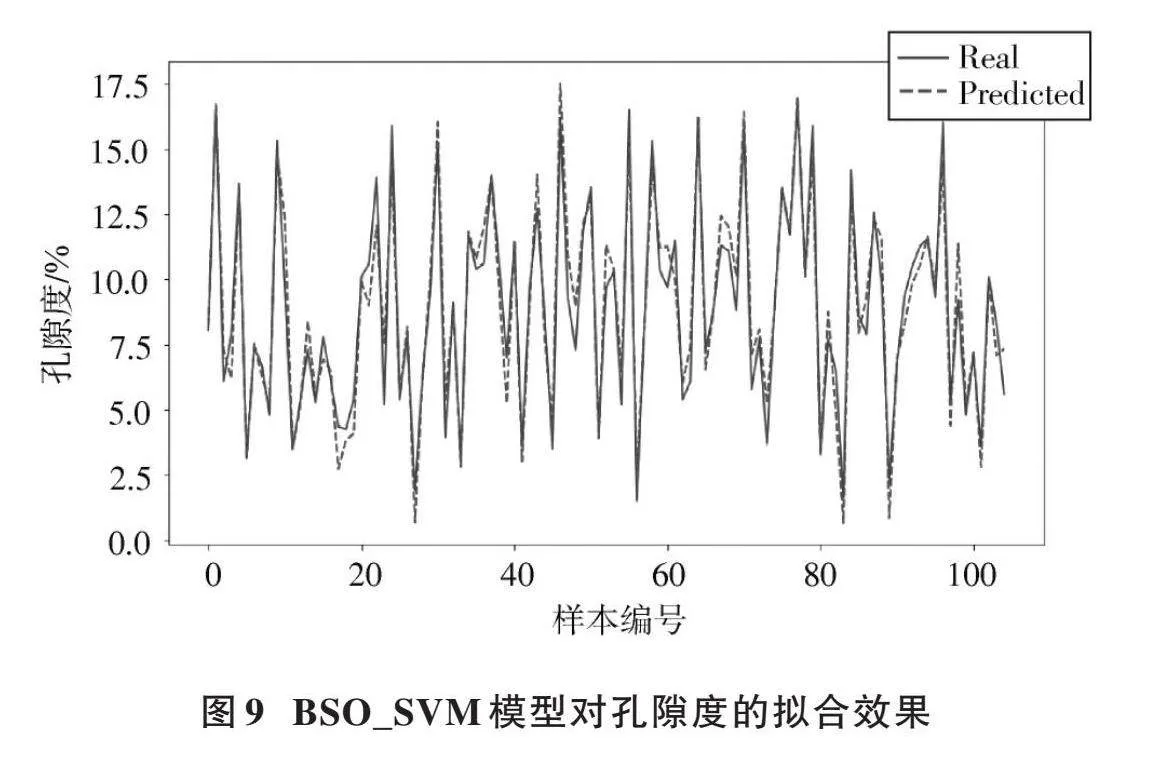
對孔隙度擬合程度如圖9所示。

根據模型算出其評估參數MSE與[R2]，如表5所示。

4.2.4" CSO布谷鳥算法對支持向量機的參數調試

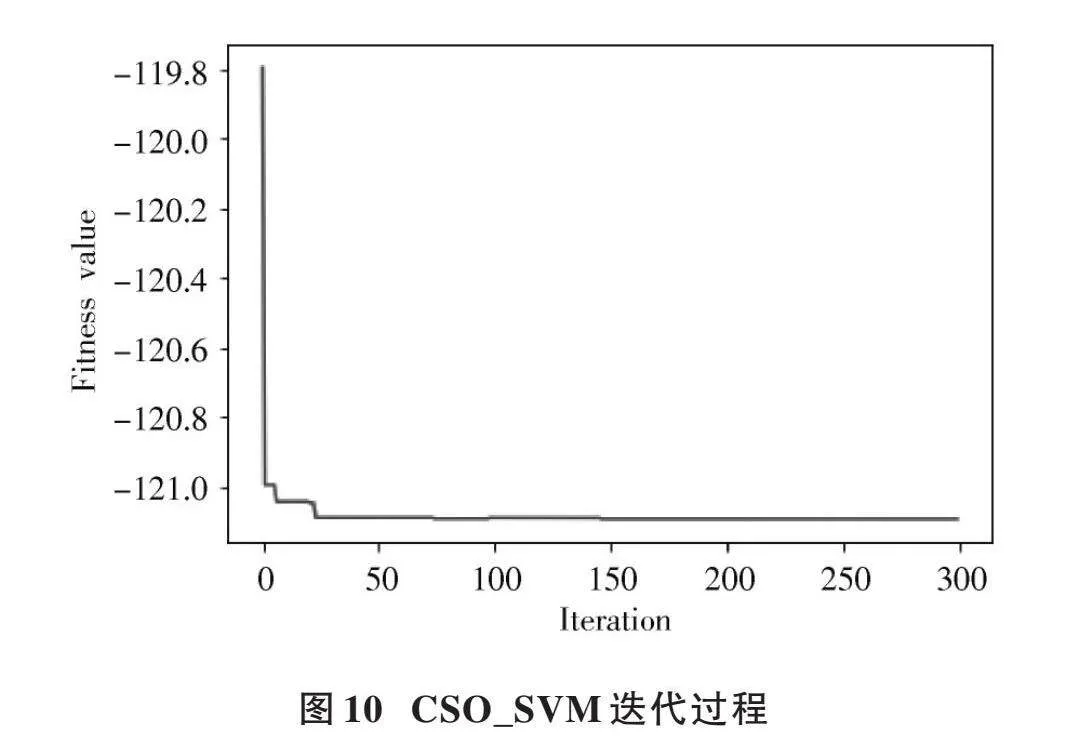
本文依靠萊維飛行能夠獲取全局最優解，經過布谷鳥算法的多層迭代如圖10所示，最后得出研究區的支持向量機最佳參數如下：

Best Regressor： SVR（[C]=4 681.0， degree=3， epsilon=1e-2， gamma=0.086 005 140 926 4， [ε]=0.17， kernel='rbf'， max_iter=-1， shrinking=True， tol=0.001）

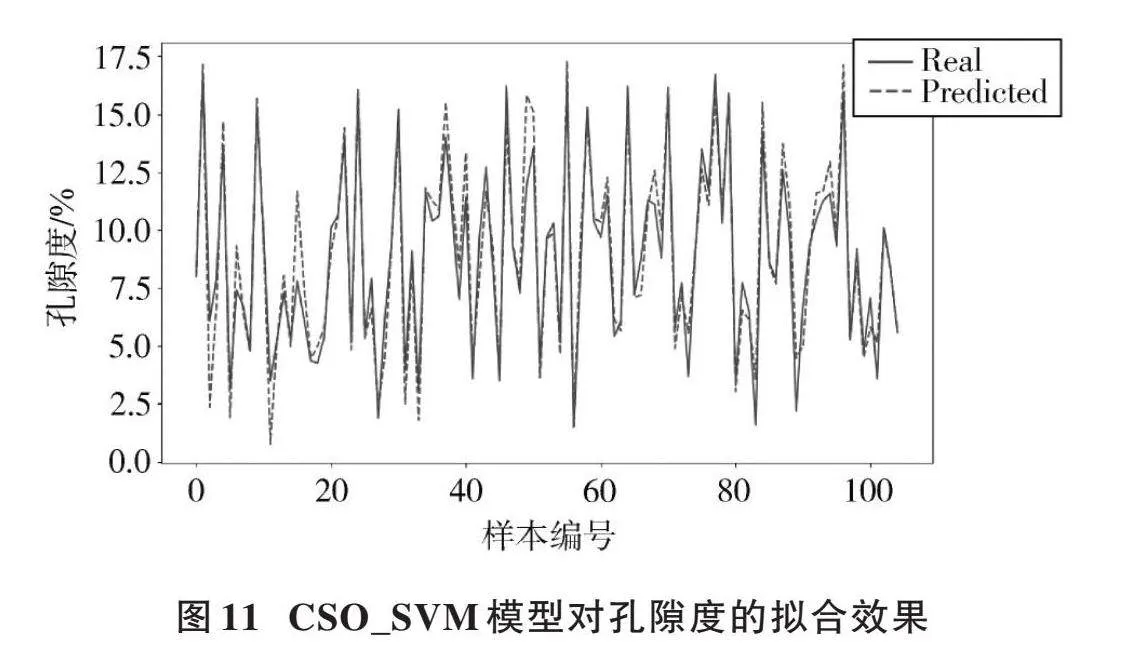
對孔隙度擬合效果如圖11所示。

根據模型算出其評估參數MSE與[R2]，如表6所示。

5" 實驗結果與分析

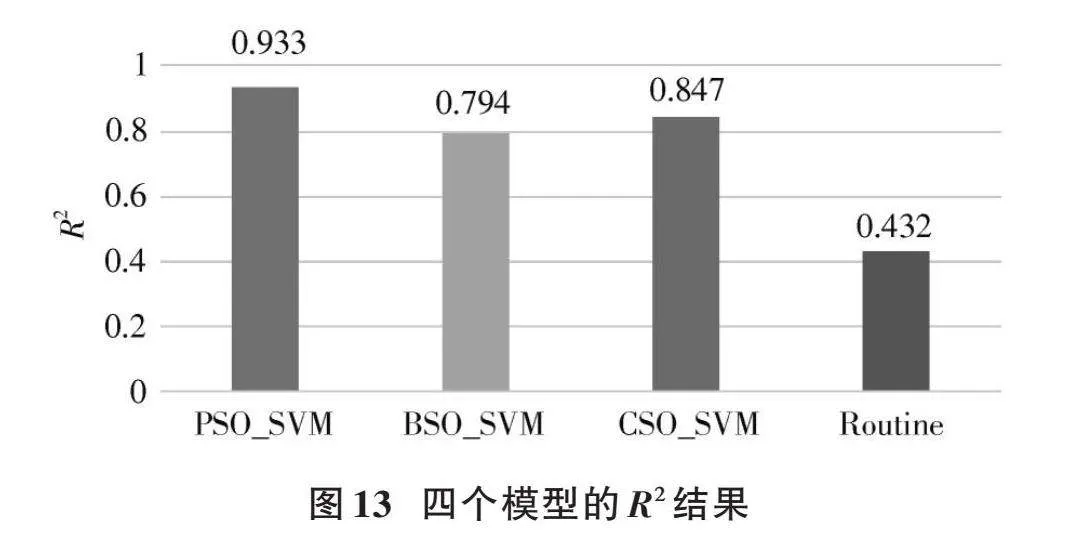
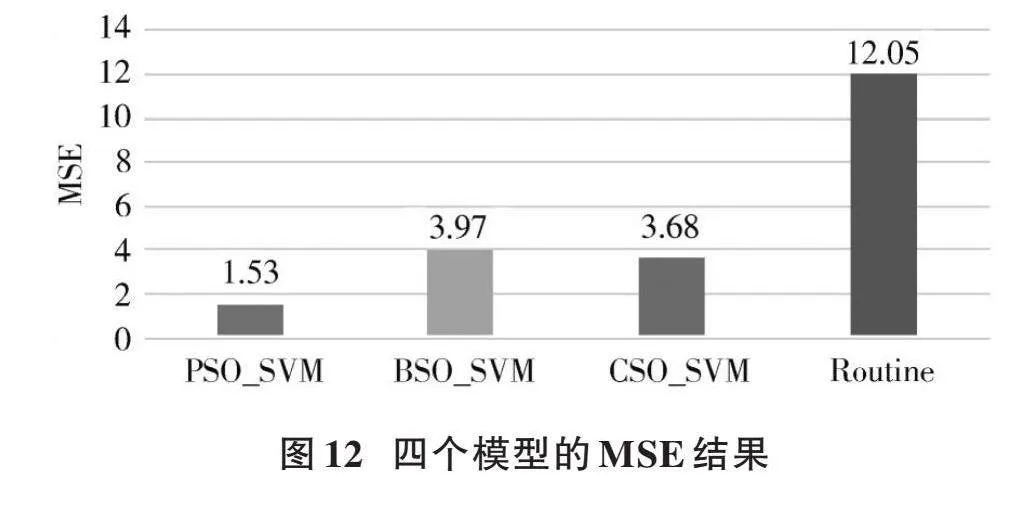
本文旨在探索PSO、BSO、CSO三種優化算法對SVM在儲層參數預測中的效果。由上述數據可以看出，本文改進后三種支持向量機（PSO_SVM、BSO_SVM、CSO_SVM）相比傳統儲層參數預測（Routine）方式，均方誤差（MSE）降低了10.52、8.08、8.37，如圖12所示。擬合度[R2]分別高出0.501、0.362、0.415，如圖13所示。

由圖12、圖13可知，對于研究區長6儲層而言，PSO_SVM模型在研究區致密砂巖儲層預測中產生了較強的適應性，相對誤差較小，精度高達0.933，且運行速度快，然而此模型在實際調參過程中，如何設置慣性因子，找到合適的數值是提高模型精確度的關鍵因素。BSO_SVM和CSO_SVM模型的預測精度均優于傳統線性回歸模型，但比PSO_SVM模型效果差，仍具有優化空間，實際應用仍然需要學者們進一步深入優化。

6" 結" 論

本文研究發現，利用PSO算法改進的SVM模型，對比傳統儲層參數預測模型和BSO、PSO改進的SVM模型，均有較大的提升，其在研究區儲層參數預測中的預測精度高、應用效果好，有效提高了研究區致密砂巖儲層參數預測的精度，為研究區的儲層精細評價提供技術支撐，為研究區致密砂巖的石油開發貢獻了新的理論基礎方向。

注：本文通訊作者為龐振宇。

參考文獻

[1] LIU Y Y， MA X H， ZHANG X W， et al. A deep?learning?based prediction method of the estimated ultimate recovery （EUR） of shale gas wells [J]. Petroleum science， 2021， 18（5）： 1450?1464.

[2] JIANG R， JI Z， MO W， et al. A novel method of deep learning for shear velocity prediction in a tight sandstone reservoir [J]. Energies， 2022， 15（19）： 7016.

[3] ZHAO F， HU X， WANG L， et al. A reinforcement learning brain storm optimization algorithm （BSO） with learning mechanism [J]. Knowledge?based systems， 2022， 235： 107645.

[4] ZHAO L， QIN X， ZHANG J， et al. An effective reservoir parameter for seismic characterization of organic shale reservoir [J]. Surveys in geophysics， 2018， 39（3）： 509?541.

[5] SIRCAR A， YADAV K， RAYAVARAPU K， et al. Application of machine learning and artificial intelligence in oil and gas industry [J]. Petroleum research， 2021， 6（4）： 379?391.

[6] 魏佳明.機器學習在儲層參數預測中的應用研究[D].西安：西安石油大學，2019.

[7] 史長林，魏莉，張劍，等.基于機器學習的儲層預測方法[J].油氣地質與采收率，2022，29（1）：90?97.

[8] CHENG S， QIN Q D， CHEN J F， et al. Brain storm optimization algorithm： A review [J]. Artificial intelligence review， 2016， 46（4）： 445?458.

[9] 張森悅，譚文安，王楠，等.基于布谷鳥搜索算法參數優化的組合核極限學習機[J].吉林大學學報（理學版），2019，57（5）：1185?1192.

[10] 何思露，韓堅華.基于布谷鳥搜索算法的SVR參數選擇[J].華南師范大學學報（自然科學版），2014，46（6）：33?39.

[11] 王作乾，范子菲，張興陽，等.2021年度全球油氣開發現狀、形勢及啟示[J].石油勘探與開發，2022，49（5）：1045?1060.

[12] 程超，李培彥，陳雁，等.基于機器學習的儲層測井評價研究進展[J].地球物理學進展，2022，37（1）：164?177.

[13] 程冰潔，徐天吉，羅詩藝，等.基于機器學習的深層頁巖有利儲集層預測方法及實踐[J].石油勘探與開發，2022，49（5）：918?928.

[14] TEMKENG S D， FOFACK A D. A Markov?switching dynamic regression analysis of the asymmetries related to the determinants of US crude oil production between 1982 and 2019 [J]. Petroleum science， 2021， 18（2）： 679?686.

[15] ALI B. Integration of impacts on water， air， land， and cost towards sustainable petroleum oil production in Alberta， Canada [J]. Resources， 2020， 9（6）： 62.

[16] DURAND?LASSERVE O. Modeling world oil market questions： An economic perspective [J]. Energy policy， 2021， 159： 112606.

[17] 王言飛.機器學習在孔隙度預測中的應用研究[D].東營：中國石油大學（華東），2020.

[18] 吳靜.致密氣儲層測井綜合評價方法研究[D].北京：中國地質大學（北京），2019.

[19] 宋歌.基于機器學習勘探資源評價方法的應用[J].計算機與網絡，2020，46（20）：46?47.

[20] 陳博.多核學習在儲層建模中的應用研究[D].西安：西安石油大學，2019.

[21] 路萍，王浩辰，高春云，等.致密砂巖儲層滲透率預測技術研究進展[J].地球物理學進展，2022，37（6）：2428?2438.

[22] 邵蓉波，肖立志，廖廣志，等.基于遷移學習的地球物理測井儲層參數預測方法研究[J].地球物理學報，2022，65（2）：796?808.

[23] 李小東.基于測井數據的儲層參數預測[D].大慶：東北石油大學，2021.

[24] 韓博華，王飛，劉倩茹，等.測井儲層分類評價方法研究進展綜述[J].地球物理學進展，2021，36（5）：1966?1974.

[25] 謝云菲.機器學習在頁巖油測井評價中的應用[D].武漢：華中科技大學，2020.