基于遺傳?模擬退火算法修正高斯煙羽模型參數

摘 "要： 高斯煙羽模型由于受到地形地貌與氣象條件等因素的影響，難以準確反映大氣的實際擴散過程。為解決上述問題，首先在經驗參數作為先驗值的基礎上，通過遺傳算法對實際觀測數據進行參數反演修正，根據觀測結果調整模型參數，提高模型的準確性；然后，為進一步優化參數修正結果，引入模擬退火算法，通過隨機搜索和逐步降溫的策略來跳出遺傳算法可能陷入的局部最優解，進一步改善模型的性能。為了評估修正效果，建立一個基于權重的模型值與觀測值之間差異的適應度函數，通過比較修正前后的誤差率來判斷參數修正對高斯煙羽模型的影響程度。仿真實驗的結果表明，所提出的遺傳?模擬退火算法模型能夠有效地修正高斯煙羽模型中的擴散參數，修正后的模型在預測污染物濃度方面的誤差率下降了89.40%。所提模型可為環境保護和污染防治提供重要的理論支撐和決策依據，具有較大的應用潛力。

關鍵詞： 高斯煙羽模型； 遺傳算法； 模擬退火算法； 參數修正； 適應度函數； 誤差率

中圖分類號： TN957.52+4?34； TP391.9 " " " " " " "文獻標識碼： A " " " " " " " " "文章編號： 1004?373X（2024）06?0009?06

Gaussian plume model parameters modification based on genetic?simulated

annealing algorithm

WANG Yanjiao， ZHANG Shaoyang， LIANG Yuquan， MA Danchen

（School of Information Engineering， Chang’an University， Xi’an 710018， China）

Abstract： Gaussian plume model is difficult to accurately reflect the actual diffusion process of the atmosphere due to the influence of topography and meteorological conditions and other factors. In order to solve the above situation， on the basis of the empirical parameters as a priori values， the actual observation data are used to carry out parameter inversion correction by means of the genetic algorithm， and the model parameters are adjusted according to the observation results to improve the accuracy of the model. A simulated annealing algorithm is introduced to further optimize the parameter correction results， which can jump out of the local optimal solutions that the genetic algorithm may fall into and further improve the performance of the model by means of the strategy of random search and gradual cooling. In order to evaluate the correction effect， a weight?based fitness function for the difference between the model value and the observed value is calculated. By comparing the error rate before and after the correction， the degree of influence of the parameter correction on the Gaussian plume model can be judged. The results of simulation experiments show that the diffusion parameters in the Gaussian plume model can be effectively corrected by means of the genetic?simulated annealing algorithm model proposed in this paper. The error rate of the corrected model in predicting pollutant concentrations is reduced by 89.40%. This experiment can provide important theoretical support and decision basis for the environmental protection and the pollution prevention， and has important application potential.

Keywords： Gaussian plume model; genetic algorithm; simulated annealing algorithm; parameter correction; fitness function; error rate

0 "引 "言

在當今的社會環境下，工業化進程的迅猛發展導致大量的廢氣排放[1]，且城市化快速擴張[2]，加劇了大氣污染問題。我國部分城市的PM2.5污染已經到達甚至超過了世界衛生組織的標準。因此，為了有效地改善大氣環境質量，減少污染物的排放和擴散對人類及生態環境帶來的危害，建立一個高效、準確的數學模型來描述和預測空氣污染物的擴散和濃度分布情況變得越來越重要。大氣擴散模型中，基于擴散實驗得到的經驗參數往往只能應用在與實驗條件相同情形下的大氣擴散過程中。由于大氣擴散模型受到不同事故的地形地貌與氣象條件等因素之間差異的影響[3?4]，導致經驗擴散參數難以廣泛地應用在實際擴散過程中。例如，IAEA使用的擴散系數[5]與USNRC使用的擴散系數[6]都有其特定環境條件，一旦環境發生較大的變化，仿真計算結果就會出現較大誤差。

為了更準確地預測事故中污染物濃度的擴散分布，通常需要對大氣擴散模型中的經驗擴散參數進行修正。這種修正方法的基本思路是：通過實際觀測數據對經驗擴散參數進行修正，使得修正后的模型計算值更加接近實際觀測值。將修正后的擴散參數應用于開始時設定的擴散模型中，模型的預測精度會大大提升。

吉志龍利用遺傳算法對拉格朗日大氣擴散模型中的PG（Pasquill?Gifford）系數進行了反演修正，并對大氣擴散模型的適應度函數進行比較尋優[7?8]。使用遺傳算法作為大氣擴散模型參數修正的方法在以往的研究中取得了一些成果[9?12]，然而，遺傳算法存在局部尋優能力較差和早熟收斂的問題，導致其反演模型具有不穩定性，因此該模型存在較大的改進空間。寧莎莎等人將遺傳算法與單純形法進行融合，改善遺傳算法陷入局部最優解的問題[13]。然而，由于單純形法主要用于線性規劃問題，對于非線性問題并不適用，因此這種模型仍然存在較大的局限性。

本文將模擬退火算法融入遺傳算法中，綜合遺傳算法尋找局部最優解的能力與模擬退火算法尋找全局最優解的能力，通過數值模擬的方法，利用遺傳?模擬退火算法對高斯煙羽模型的擴散系數進行參數修正，結合適應度函數判斷此算法的參數修正能力，并將參數修正前后的污染物濃度與實際觀測值進行對比，驗證修正后的模型預測能力。

1 "高斯煙羽模型

高斯煙羽擴散模型是一種常見的空氣污染模型，它用于對大氣中的污染物濃度的預測，在城市規劃、環境保護、應急管理等領域中發揮著重要作用。該模型是基于高斯分布的假設，排放源釋放的污染物在空間中呈現出類似于圓錐形狀的分布。如圖1所示，坐標原點為污染物的排放源，將x軸正方向設定為平均風向，y軸垂直于x軸設定為垂直風向，z軸正方向垂直于水平面向上。

在構建高斯煙羽擴散模型時需假設：

1） 大氣穩定均勻且風速不變。

2） 污染物濃度在y、z軸上的分布符合正態分布。

3） 污染物在擴散過程中不分解、不沉降，且不受化學反應的影響。

4） 污染源的源強連續且均勻。

基于上述假設，經過推導得出連續釋放的高斯地面點源擴散公式如下：

[Cx，y，z=Qπ?u?σy?σz?exp-12y2σ2y+z2σ2z] " " （1）

式中：[Cx，y，z]表示監測點在[x，y，z]位置處的污染物濃度，單位為mg/m3；[σy]、[σz]分別表示水平、垂直方向的標準差，即[y]、[z]方向的擴散參數；[u]表示平均風速，單位為m/s；[Q]表示釋放源強，單位為g/s；[x]表示下風向軸上空間點到點源的距離，單位為m；[y]表示下風向軸垂直方向上空間點到點源的距離，單位為m；[z]表示空間點的高度，單位為m。

針對大氣環境中穩定度和下風向距離這兩個因素的影響，目前已使用多種經驗公式來計算擴散參數，其中最為常用的是PG擴散曲線，該曲線的計算方法可以較為準確地反映出大氣穩定度和下風向距離對擴散過程的影響。PG曲線具體公式如下：

[σx=σy=py·xqy] " " " " "（2） " " " " " "[σz=pz·xqz] " " " " " " "（3）

式中：x表示煙團中心距離釋放源的下風向距離，單位為m； [py]、[qy]、[pz]、[qz]為PG擴散系數，由事故發生當時的地形地貌與氣象條件等因素決定。模型中假設x、y方向上的濃度具有相同的分布規律。

PG擴散曲線是根據特定情形下的實驗數據推導而來的，一旦將PG擴散曲線應用于與其實驗環境有較大不同的環境時，模型的預測結果會出現較大的誤差。為了提高大氣擴散模型的適用性和準確性，可以使用實際觀測值對原始的PG系數進行修正，公式如下：

[p'y=rpy·py] " " " " " " "（4）

[q'y=rqy·qy] " " " " " " "（5）

[p'z=rpz·pz] " " " " " " （6）

[q'z=rqz·qz] " " " " " "（7）

通過找到一組合適的參數[rpy]、[rqy]、[rpz]、[rqz]，使得計算值與測量值之間的差距盡可能小，以對PG系數進行修正，通過不斷調整這些參數的值，達到使模型預測結果最接近實際觀測值的目的。經過修正的參數可以大幅度提高擴散模型的預測精度和適用范圍。

2 "算法設計實現

2.1 "遺傳算法與模擬退火算法融合

本文采用遺傳算法和模擬退火算法求解式（1）。遺傳算法[14]是模仿自然界生物進化機制發展起來的隨機全局搜索和優化方法，即在全局將初始數據以設定的適應性函數為目標進行計算，這時將更接近實際的數據選擇出來，再進行交叉、變異得到新的數據，此時將符合要求的數據作為候選解，不斷重復上述操作，直到可以從候選解中挑選出與最優解相近的解。本文使用格雷編碼將問題的解編碼為基因型，用來提升遺傳算法的局部搜索能力。但是，經過遺傳算法逐步挑選得到的數據可能陷入局部最優解。為解決該問題，本文引入了模擬退火算法。

模擬退火算法[15]是基于物理學中固體物質的退火過程原理衍生出的一種通用的優化算法，即從設定的初始溫度開始，按照設定的溫度衰減系數逐步降低溫度，在每次降低溫度后通過增加隨機擾動生成新的解，并以一定的概率去接受新的解，直到溫度下降到設定的終止溫度時結束。由于該算法在搜索最優解的過程中引入了隨機因素，即以一定概率去接受一個比當前解要差的解，因此有可能跳出當前所處的局部最優解，最終收斂到全局的最優解。將遺傳算法與模擬退火算法相結合，能夠最終得出解空間中的最優解。

2.2 "適應度函數

在PG系數修正的過程中，需使用適應度函數來對觀測值與計算值之間的差距進行度量。適應度函數的值越小，則說明觀測值與計算值之間的差距越小，所以適應度函數的構造在本實驗中起到至關重要的作用。針對不同的應用場景，適應度函數的設計與構造應結合具體問題的要求而定，適應度函數的選取將直接影響到遺傳?模擬退火算法的性能。下面對本文修正模型中的適應度函數進行分析構造。

由于地形地貌與氣象條件等因素造成的觀測條件不同，不同觀測點所處的位置不同，都會對觀測值造成影響，所以經過實際觀測得到的觀測信息的可信度不同。

針對上述因素，在選取適應度函數時，應符合下面兩點要求：

1） 對于某個觀測站，當模型的計算值與實際的觀測值越接近時，適應度函數的值應當越小；

2） 在設計適應度函數時，針對不同的觀測站應設置不同的權重，觀測值更準確的觀測站點占較高的權重，反之，占較低的權重。

基于上述兩點要求，本文結合最小二乘法對適應度函數進行構造，公式如下：

[fitness=i=1NOiCi-Oi2i=1NOi] （8）

式中：i表示第i個觀測點；N表示觀測點總數；[Oi]為第i點的實際測量值；[Ci]為擴散模型在第i點的濃度計算值。

根據滿足上述要求而構造的適應度函數表達式可知，適應度函數的值與[Ci-Oi2]成正比，即當本文模型的計算值與實際觀測值越接近時，適應度函數的值越小。

2.3 "選擇算子

本文在遺傳算法的選擇階段，采用輪盤賭法對數據進行選擇。先通過公式（9）計算出該種群中某個個體被選擇的概率，適應度更高的數據更容易通過輪盤賭法被選中，即數據通過該選擇法被選擇的概率與該數據的適應度大小成正比。

[Pi=fij=1N′fj] " " " " " " "（9）

式中：[Pi]為第i個個體被選中的概率；[fi]為第i個個體的適應度值；N′為種群規模。該方法簡單易行，可以保證適應度較高的個體更多地被選擇和遺傳，有利于優化算法的收斂性和搜索能力。

2.4 "交叉算子

交叉算子在遺傳算法中起到十分關鍵的作用，交叉算子通過模擬自然界生物進化的過程來增加種群的豐富度，擴大尋找最優解的范圍，使遺傳算法的全局搜索能力得以增強。為使遺傳算法可以更好地探索新的解空間，本文采用單點交叉方法，設置交叉概率為0.9。

2.5 "變異算子

變異算子在遺傳算法中的作用是：產生一部分新的變異個體，用以提高種群的多樣性。變異算子還可以提高遺傳算法向最優解的收斂速度，但為防止變異過程中破壞到最優解附近的數據，應設置一個較小的變異概率，本文設置變異概率為0.01。

2.6 "模擬退火算子

遺傳算法得到的數據經過小幅度擾動得到新的解后，使用Metropolis函數來判斷是否接受新解，公式如下：

[Δf=fnew-f] " " " " " "（10）

式中：f表示未增加擾動時解的適應度函數值；[fnew]表示對當前解加入擾動后得到新解的適應度函數值。若[Δflt;0]，則接受新解；否則按照概率為[exp-ΔfkT]來判斷是否應該接受此解，其中k表示溫度下降速率，本文設置為0.85。不斷重復模擬退火操作，直到該算法達衡狀態為止。

在遺傳?模擬退火算法中，隨著迭代次數的增加，PG系數逐漸向最優解“進化”，此時，模型計算值不斷逼近實際觀測值，使得適應度函數的值逐漸收斂于最優解。

3 "算法仿真分析

3.1 "仿真方法

為了驗證利用遺傳?模擬退火算法對擴散系數進行修正之后模型預測的準確度，本文采用數值模擬的方法對PG系數加上修正參數之后的模型進行觀測，所采用的方法如下：

1） 設置各項模型參數，包括源強、平均風速、釋放高度、PG系數等。

2） 運行擴散模型得到濃度分布情況，從中選取出監測點，對其進行加噪并設為觀測值。

3） 對原有PG系數進行加噪，得到遺傳?模擬退火算法修正的先驗值。

4） 運行遺傳?模擬退火算法對PG系數設定值進行修正。以加噪后得到的觀測值為標準，利用適應度函數進行評判，逐步縮小誤差，最終得到修正后的PG系數。

3.2 "仿真設置

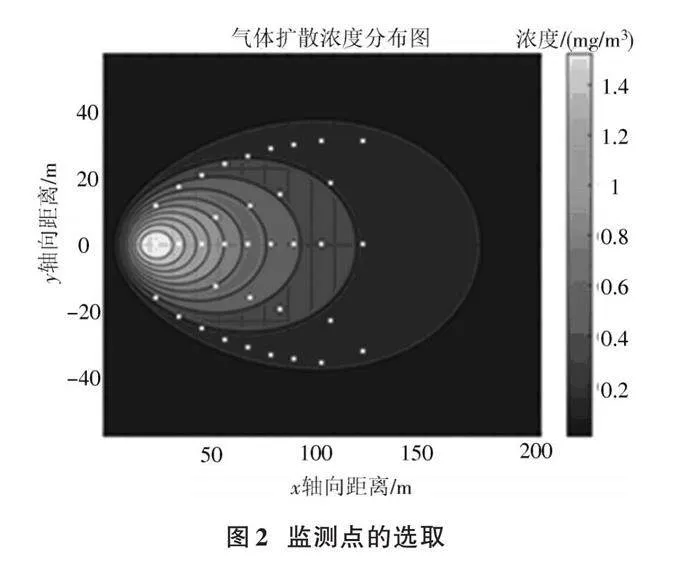
為了方便模擬仿真，本實驗將釋放源的源強固定為400 g/s，并將其所在位置設為坐標原點，平均風速設為0.5 m/s，實驗所在地的大氣穩定度設為A?B。本實驗監測點的選取如圖2所示。

PG系數種群利用Matlab自帶的遺傳算法工具包中的crtbp函數生成。在利用遺傳?模擬退火算法進行優化時，本實驗將4個修正參數轉化為二進制，以便更好地使個體進行交叉和變異。在實驗中，待求解PG系數的修正參數被編碼為浮點數[rpy]、[rqy]、[rpz]、[rqz]，這些參數的取值范圍被限定在（0，2.0]之間。

3.3 "仿真結果分析

通過數值模擬的方法分析遺傳?模擬退火算法修正后的PG系數對模型計算結果準確性的影響，可以得到如圖3所示的仿真結果。為使圖像效果更直觀明顯，在繪制圖像時，將圖像的縱軸設置為適應度值的倒數。

從圖3的仿真結果中可以看出，隨著迭代次數的增加，適應度函數值的倒數在總體趨勢上是遞增的。說明適應度函數的值在總體上是減小的，即高斯煙羽模型的計算值與實際觀測值之間的差距在總體上減小。盡管中間某些代的適應度值過高或過低，但這是由于遺傳算法本身變異產生的結果，總的來說，適應度函數還是“進化”得越來越好，說明算法具有很好的收斂性。

在遺傳算法運行結束后，繼續使用模擬退火算法對遺傳算法的結果進行優化。多次實驗得到的仿真結果如圖4所示。從模擬退火算法的仿真結果來看，經過模擬退火算法的進一步修正，適應度值的倒數進一步增大，即PG系數的修正效果進一步提升。模擬退火算法幫助適應度函數跳出了局部最優解，最終接近全局最優解。

經過多次仿真實驗可知，適應度函數值經過遺傳算法幾十代的迭代之后開始趨于穩定。模擬退火算法可以使函數在遺傳算法產生的結果上進一步優化，以接近全局最優解，所以兩者結合的遺傳?模擬退火算法在收斂時間、進化代數、全局搜索概率等方面都有著很高的效率和性能。

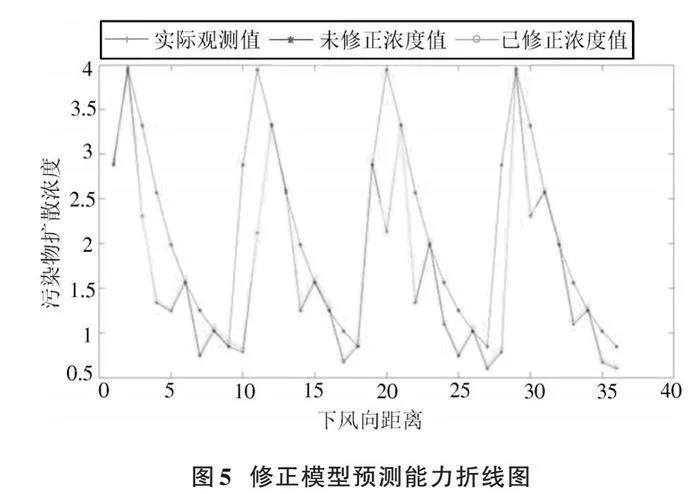
將經過遺傳?模擬退火算法修正前后的PG系數分別代入到高斯煙羽模型中，求得大氣污染物濃度的計算值，并將其與實際觀測值進行比較，結果如圖5所示。

將圖5中的部分數據整理，結果如表1所示。通過計算參數修正前后觀測值與實際觀測值之間的誤差率，可以評估算法對于污染物濃度的準確性和精度。如果修正后的誤差率較低，則說明本文提出的算法能夠更好地模擬實際觀測值，表明該算法性能較好；相反，如果修正后的誤差率仍然較高，則表示該算法有待改進。

由表1可知，經過優化后的模型計算值相較于未優化的計算值誤差率下降了89.40%。在實際測試數據的驗證下，經過修正的模型預測能力良好，可供實際應用。

4 "結 "論

本文使用遺傳?模擬退火算法對高斯煙羽模型中的參數修正問題進行研究，利用模擬實際大氣情況的觀測值對PG系數進行反演修正，使得經過修正后的高斯煙羽模型能更準確地反映實際大氣情況。由數值模擬結果可知，通過遺傳算法可以產生一個較優的解，在這個解的基礎上繼續使用模擬退火算法優化使其不斷接近最優解，最后產生的PG系數可以使得高斯煙羽模型的計算值與實際測量值的誤差達到最小，從而使得該模型的預測值更加精準。實驗證明，通過遺傳?模擬退火算法對高斯煙羽模型中的參數修正后，高斯煙羽模型的預測能力得到了很大的提高。

注：本文通訊作者為王彥驕。

參考文獻

[1] 孫濤，汪根寶.利用高斯煙羽模型設計尾氣放空煙囪的探討[J].化工設計，2018，28（1）：12?15.

[2] 阮順領，金裕，李玲燕，等.施工場所點源揚塵擴散特征模擬分析[J].環境科學與技術，2019，42（z2）：275?279.

[3] 徐曉波.關中地區點源大氣污染物擴散數值模擬[J].環境保護科學，2018，44（3）：98?101.

[4] 毛敏娟，杜榮光，胡德云.氣候變化對浙江省大氣污染的影響[J].環境科學研究，2018，31（2）：221?230.

[5] IAEA. Atmospheric dispersion model for application in relation to radionuclide release [M]. Austria： International Atomic Energy Agency， 1986.

[6] USNRC. Methods for estimating atmospheric transport and dispersion of gaseous effluents in routine release from light water cooled reactor [M]. Washington： Nuclear Regulatory Commision， 1977.

[7] 吉志龍，馬元巍，王德忠.遺傳算法動態修正核素大氣擴散模型的適應度函數研究[J].核技術，2014，37（4）：60?65.

[8] 吉志龍.基于遺傳算法的氣載核素大氣擴散反演模型研究[D].上海：上海交通大學，2014.

[9] HAUPT S E， YOUNG G S， ALLEN G T. Validation of a receptor?dispersion model coupled with a genetic algorithm using synthetic data [J]. Journal of applied meteorology and climatology， 2006， 45（3）： 476?490

[10] JEONG H J， KIM E H， SUH K S， et al. Determination of the source rate released into the environment from a nuclear power plant [J]. Radiation protection dosimetry， 2005， 113（3）： 308?313.

[11] ALLEN C T， YOUNG G S， HAUPT S E. Improving pollutant source characterization by better estimating wind direction with a genetic algorithm [J]. Atmospheric environment， 2007， 41（11）： 2283?2289.

[12] QIN Y， ODUYEMI K. Atmospheric aerosol source identification and estimates of source contributions to air pollutions in Dundee， UK [J]. Atmospheric environment， 2003， 37（13）： 1799?1809.

[13] 寧莎莎，蒯琳萍.混合遺傳算法在核事故源項反演中的應用[J].原子能科學技術，2012，46（z1）：469?472.

[14] 常洪江.遺傳算法綜述[J].電腦學習，2010（3）：115?116.

[15] 龐峰.模擬退火算法的原理及算法在優化問題上的應用[D].長春：吉林大學，2006.