基于LADRC的四輪全向Mecanum輪機器人運動控制研究

摘 "要： 近年來，移動機器人在巡檢作業、智能電器、無人駕駛等領域的作用日益顯現。全向移動機器人由于結構的特殊性和運動控制的復雜性，采用經典控制方法如比例積分微分控制、線性二次型調節控制等很難實現穩定的控制。針對全向移動機器人易受到外界擾動及其建模不精確的問題，進行四輪全向Mecanum輪機器人的運動控制系統設計。使用擴張狀態觀測器進行機器人總擾動的實時估計，完成LADRC控制器的設計。實驗結果表明，相較于傳統控制方法，基于LADRC的控制器能夠更好地抑制外部干擾，減小運動誤差，并提高機器人的運動精度和魯棒性。

關鍵詞： 四輪全向Mecanum輪機器人； LADRC控制器； 運動學模型； 擴張狀態觀測器； 抗擾特性； 軌跡跟蹤

中圖分類號： TN876?34； TP242 " " " " " " " " " "文獻標識碼： A " " " " " " " " " " 文章編號： 1004?373X（2024）06?0165?06

Research on four?wheel omnidirectional Mecanum wheel robot motion

control based on LADRC

JIANG Huayang1， WU Tao1， 2， LI Mingshuo1， SUN Jiahui1， REN Jianxin1

（1. Faculty of Mechanical and Electrical Engineering， Kunming University of Science amp; Technology， Kunming 650500， China;

2. Computer Center， Kunming University of Science amp; Technology， Kunming 650500， China）

Abstract： In recent years， the role of mobile robots has become increasingly evident in fields such as inspection tasks， smart appliances， and autonomous driving. Due to the particularity of the omnidirectional mobile robot structure and the complexity of motion control， classic control methods such as proportional?integral?derivative control and linear quadratic regulation control are challenging to achieve stable control. In allusion to problem that omnidirectional mobile robot is susceptible to external disturbance and its modeling is not accurate， the motion control system of four?wheel omnidirectional Mecanum wheel robot is designed. A real?time estimation of the overall disturbance for the robot is accomplished by means of an extended state observer， and the design of the LADRC （linear active disturbance rejection control） controller is completed. The experimental results show that， in comparison with traditional control methods， the controller based on LADRC can better suppress external interference， reduce motion errors， and improve the motion accuracy and robustness of the robot.

Keywords： four?wheel omnidirectional Mecanum wheel robot; LADRC controller; motion model; expansion state observer; immunity characteristics; trajectory tracking

0 "引 "言

隨著科學技術的不斷進步和人們對自動化技術的需求增加，移動機器人作為一種具有廣泛應用前景的智能機器人系統，受到了越來越多的關注和研究[1?2]。移動機器人的運動控制是其關鍵技術之一，直接影響到機器人在不同環境下的運動能力和任務執行效果。針對移動機器人運動控制領域的研究，許多方法和技術已經被提出和應用[3]。例如：線性控制（PID控制）、模糊控制、神經網絡控制、最優控制（LQR和MPC）以及自適應控制，不同的運動控制方法在不同的場景和應用中具有各自的優劣勢。本文主要針對移動機器人自身擾動和外界干擾對其運動控制的影響進行進一步研究，因此選擇有效抑制外部干擾和未建模動態系統擾動的自適應控制方法。線性自抗擾控制（Linear Active Disturbance Rejection Control， LADRC）是一種對系統的干擾進行實時估計和補償，從而消除或減小干擾對系統性能的影響的控制方法[4]。研究者們利用LADRC算法設計了移動機器人的路徑跟蹤控制系統。通過自適應調節控制參數，該系統能夠實現對移動機器人在不同路面和環境下的軌跡跟蹤控制[5?7]。另外，研究者們提出了基于LADRC的輪式機器人速度和位置控制方案，有效解決了輪式機器人在不同工作負載和路面條件下的控制問題[8]。

本文主要針對基于LADRC四輪全向移動機器人的運動控制策略展開相應研究。首先，建立機器人數學模型；其次，進行擴張狀態觀測器和LADRC控制器的設計；最后，通過對比實驗來分析所提出的LADRC控制策略與其他控制方法的優劣勢。

1 "機器人數學模型

1.1 "運動學建模

四輪全向Mecanum輪機器人的位置和姿態在二維平面運動具有各自的作用，運動學建模過程同時定義全局坐標系與機器人坐標系。運動學模型在理論分析層面闡述了機器人運動控制單元驅動4個Mecanum輪完成全方位移動的過程，為了簡化建模和分析過程，在做出理想條件假設的情況下，分析機器人的運動學模型[9?11]。

建立如圖1所示的運動學模型，平面坐標系[XwOwYw]表示機器人的絕對坐標系，[XmOmYm]坐標系的原點與4個Mecanum輪的幾何中心點重合，定義Mecanum輪坐標系[Oi（i=1，2，3，4）]，[Xm]軸、[Ym]軸分別與[Xw]軸、[Yw]軸平行且方向一致。

如圖1所示，[2x]表示車輪[Xm]軸方向的中心距離；[2y]表示車輪[Ym]軸方向的中心距離；[Om]點為移動機器人幾何中心；4個Mecanum輪的自轉角速度為[ωi]（i=1，2，3，4），分別表示左前、右前、左后及右后輪；[vg]為輥子的線速度；Mecanum輪的半徑為R；[vtx]表示[Xm]軸的線速度；[vty]表示[Ym]軸的線速度；[ω]表示機器人角速度；[α]為輥子軸線和輪轂軸線之間的夾角。

通過對整理角速度得到的機器人逆運動學解算矩陣進行矩陣變換，并代入本課題使用的Mecanum輪，可得全方位移動機器人在理想條件下的正運動學公式為：[vtxvtyω=R4x+y·x+y-x+yx+y-x+yx+yx+yx+yx+y-111-1ω1ω2ω3ω4] " " " " （1）

式（1）表示全方位移動機器人在理想條件下的正運動學公式，雅克比矩陣需滿秩，即[rank（K） = 3]，4個Mecanum輪的轉速與機器人的運動一一對應，調節各輪的轉速即可實現機器人的全向移動。系統有3個被控量和4個控制輸入量，通過控制輸入量之間的相互配合，將各輪的角速度作為機器人運動的控制輸入，對機器人前后、左右以及斜向平移等運動情況進行分析，就能夠使機器人按照所規劃的軌跡運動。這就是理想條件下四輪全向Mecanum輪機器人運動學建模的理論基礎。

1.2 "動力學建模

本文研究的四輪全向Mecanum機器人，每個Mecanum輪外緣上都有許多傾斜45°安裝的小輥子，機械系統結構較復雜，其運動控制系統具有非線性、多變量的特點。本文選擇拉格朗日方法求解機器人的動力學模型[12]。

從機械動能守恒的角度進行分析，機器人運動動能為：

[Ek=12mv2tx+v2ty+12Jzω2+12Jωi=14ω2i] "（2）

式中：[vtx]、[vty]、[ω]表示在其幾何中心點位置的水平、豎直線速度與角速度；[ωi]（i=1，2，3，4）表示4個輪的自轉角速度；[m]為移動機器人的總質量；[Jz]為機器人繞[z]軸的轉動慣量；[Jω]代表Mecanum輪繞其轉軸的轉動慣量。

系統考慮了運動過程中輪與地面產生的摩擦力，因此系統瑞利耗散函數可表示為：

[Φ=12μω21+ω22+ω23+ω24] " （3）

式中[μ]表示輪與地面的摩擦系數。

根據機器人的逆運動學模型，令[l = x+y]，將所得結果代入式（2）和式（3）整理后，放入第二類拉格朗日方程，可得如下公式：

[Ax+Bx=FxAy+By=FyCθ+l2Bθ=τA=m+4JωR2，B=4μR2，C=Jz+4Jωl2R2] " （4）

式中：廣義力[Fx]、[Fy]為[Xw]和[Yw]方向上的總驅動力；[τ]表示繞[z]軸旋轉的總轉矩。

在機器人坐標系下，沿[Xm]和[Ym]軸的驅動力[F′x]和[F′y]以及繞[Zm]軸的合力矩[τ]與電機驅動力矩[τi]的關系式如下：

[F′xF′yτ=12RPτ1τ2τ3τ4，P=1111-11-11-l-lllτ1τ2τ3τ4=2RPTPPT-1F′xF′yτ] （5）

系統的總驅動力通過[F′x]與[F′y]二力合成所得，通過坐標變換矩陣可將驅動力在全局坐標系下的[Xw]和[Yw]軸中進行重新分解，進而獲得[Fx]與[Fy]，因此轉換關系式如下：

[FxFyτ=12RwmRTPτ1τ2τ3τ4] " （6）

式中[wmR]表示全局坐標系與機器人坐標系轉換矩陣。

綜合式（4）～式（6）可得式（7），即控制輸入為各Mecanum輪電機驅動力矩，狀態變量為四輪全向機器人位姿[q]的系統動力學模型。

[A000A000Cq+B000B000l2Cq=12RwmRTPτ1τ2τ3τ4] "（7）

2 "機器人LADRC控制器設計

2.1 "控制系統設計

四輪全向Mecanum輪機器人的建模過程存在一定誤差，機器人系統內部的不確定因素難以消除，也容易受到外界環境的干擾。針對目前機器人的控制策略存在依賴被控對象的數學模型而導致抗干擾性能較差等問題，本文采用LADRC對機器人的運動控制問題進行研究。

由式（7）可知，系統由4個電機提供的驅動力矩作為輸入，但是狀態量[q]只有3個，因此系統存在控制耦合，需要進行變量代換實現控制解耦，將系統簡化為[x]、[y]和[θ]三個獨立的單輸入單輸出系統。根據式（5）～式（7），且由式（6）最終可得到新的動力學方程[13]：

[Mq+Cq =u] （8）

2.2 "擴張狀態觀測器的設計

擴張狀態觀測器是一種用于系統狀態估計的技術，它可以提高控制器對系統狀態的感知能力。本節選擇線性擴張狀態觀測器LESO[14?15]對四輪全向Mecanum輪機器人的總擾動進行實時估計，將式（8）改寫為：

[q=q2q2=q = M-1u-Cq+f] "（9）

式中：[f]為系統總擾動，不僅包含系統耗散力為代表的系統非保守力，同時也包括系統運動過程中的外部環境因素干擾以及建模過程中模型不精確導致的不確定性等內部擾動。

用[z1]、[z2]、[z3]分別對[q]、[q]、[f]進行估計，根據四輪全向Mecanum輪機器人的系統方程式（9），設計LESO如下：

[z1=z2+β1q1z2=z3+M-1u-Cq+β2q1z3=β3q1] "（10）

式中：[q1]作為[q]的估計誤差，并且[q1=q-q]，[q]表示機器人的位姿估計值；[β1]、[β2]、[β3]為設計的觀測器增益，觀測器增益的取值可通過極點配置法計算得到。LESO的特征方程如下：

[λ0（s）=s3+β1s2+β2s+β3=0] （11）

為了參數調試方便，將LADRC的調參問題與觀測器帶寬相聯系，特征方程的極點都配置在[-ωo]處，[ωo]作為觀測器帶寬，這樣式（11）可以改寫為：

[λ0（s）=s3+β1s2+β2s+β3=s+ωo3=0] （12）

通過合理設計LESO以及正確配置觀測器增益的值，LESO可以較為精準地估計系統方程的各狀態變量和擴張的狀態變量，能夠實現[z1→q]，[z2→q]，[z3→f]。LESO對于不確定情況下四輪全向Mecanum輪機器人的運動控制具有關鍵作用。

2.3 "LADRC控制器的設計

對于四輪全向Mecanum輪機器人而言，其系統帶寬受車體硬件等物理因素的限制，不能無限增大。對于實時改變的系統，LESO估計系統總擾動的效果并不理想，導致僅靠PID控制不能獲得較好的控制性能，因此將設計的控制器分為擾動補償部分和軌跡跟蹤部分，一部分控制系統的誤差，一部分控制系統的穩定。這樣既能讓移動平臺快速穩定運行，又能使系統的誤差較小。

控制器的擾動補償部分[16]公式如下：

[u1=-Mz3] "（13）

式中[z3]包含了建模過程的不確定性、機器人運動過程中系統參數的改變以及外界環境因素對機器人產生的干擾。在控制器中對系統的總擾動[z3]進行補償，進而實現對四輪全向Mecanum輪機器人的精準控制。

控制系統設計的要求是軌跡跟蹤，為此軌跡跟蹤部分設計如下：

[u2=Mqd+KPqd-z1+KDqd-z2+M-1Cq] "（14）

式中：[qd]表示機器人的期望位姿；[KP]和[KD]分別為比例和微分的放大系數。

[ωci=ωc1+aqi+b， "i=1，2，3] "（15）

式中：[ωc]表示控制器初始帶寬；[qi]代表[q]的第[i]個分量。

將式（13）與式（14）聯立，可得含有擾動補償的LADRC公式為：

[u=u1+u2=Mqd+KPqd-z1+ " " " "KDqd-z2+M-1Cq-z3] " " （16）

由[u=Bτ]可知，[u]為系統的虛擬控制量，其中[τ=R2P1wmRu]，令[B1=R2P1wmR]，可得含有擾動補償的非線性控制器為：

[τ=B1u=B1Mqd+KPqd-z1+ " " " "KDqd-z2+M-1Cq-z3] （17）

根據[ωci]公式可知：當速度[qi]遠大于[a]時，各通道的控制器增益近似等于初始增益；當速度[qi]遠小于[a]時，控制器增益比初始增益大，既能提高控制精度，又能避免執行器飽和。控制器最大增益通過式（15）中參數[a]和參數[b]確定，可以有效避免控制器因帶寬過大造成的系統不穩定等問題。

在控制器中，[-Mz3]作為擾動補償項，其中[z3]表示系統的總擾動，通過補償擾動能夠最大程度地降低不確定性對系統的影響，使得控制器擁有良好的主動抗擾性能。控制器中既包含已知數學模型的信息，也包含給定的軌跡信息，減輕了控制器的計算負擔，減少了擾動估計的滯后，改善了控制器的控制性能。

3 "仿真結果與分析

3.1 "對比仿真實驗參數設置

仿真的參考軌跡設置為具有不穩定性的圓形，在軌跡跟蹤過程中機器人的運動方向會發生變化，這一過程相當于在軌跡中添加擾動，用這種方法來證明LADRC算法的抗擾特性。本文將圓形的直徑設為[1 m]，參考軌跡為：[x=cost]，[y=sint]，[θ=t]，機器人的線速度取[0.072 m/s]，角速度取4.5 rad/s。為驗證LADRC的優勢，仿真過程中與工業中常用的PID控制器進行對比。LESO的觀測器帶寬[ωo=2]，線速度LADRC控制器的參數為：[Kp1=5 000A]，[Kd1=100A]；角速度LADRC控制器的參數為：[Kp2=5 000C]，[Kd2=100C]。設置線速度PID控制參數為：[KP1=100A]，[KD1=100A]；角速度PID控制參數為[KP2=100C]，[KD2=100C]。初始條件下，將四輪全向Mecanum輪機器人的初始值設置為：[x=0.5 m]，[y=0.2 m]，[θ=0]；仿真時間設置為[10 s]，采樣頻率為[500 Hz]。四輪全向Mecanum輪機器人模型參數設定如表1所示。

3.2 "對比仿真結果分析

為了進一步對LADRC算法性能進行量化，從而對控制器的有效性進行直觀對比，采用累積絕對跟蹤誤差作為評價指標，定義如下：

[T（exy）=0Tex+eydtT（eθ）=0Teθdt] " （18）

式中：[ex]、[ey]、[eθ]為控制誤差。

通過式（18）可知，累積絕對誤差從全局上對LADRC的控制效果進行評定，評價指標表示移動機器人軌跡跟蹤累積的跟蹤誤差的大小，累積絕對跟蹤誤差越小，表示機器人的軌跡跟蹤性能越好，即控制器性能越好。

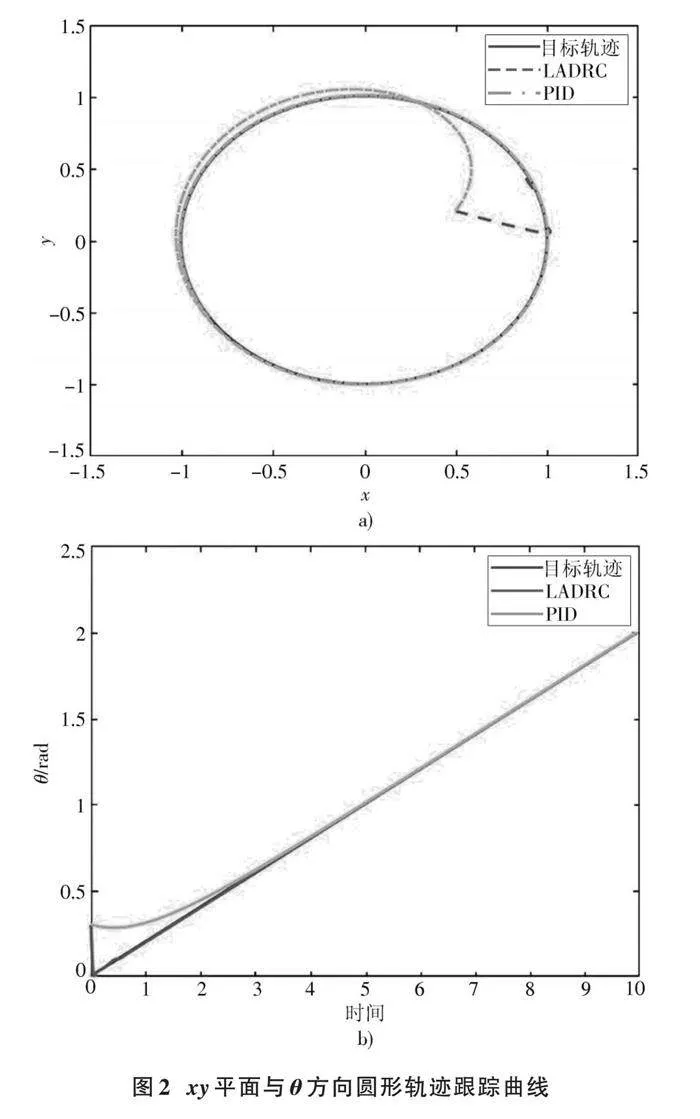
本次仿真中設置機器人進行低速運動，以盡可能減少系統擾動影響。兩種控制算法對于圓形軌跡的跟蹤性能如圖2所示。

從圖2機器人的軌跡跟蹤曲線可知：一方面LADRC算法的軌跡跟蹤性能在xy平面以及θ方向較好，能更快地到達穩態，機器人實際位姿軌跡與期望軌跡相差較小；另一方面，LADRC算法誤差較小，而PID算法存在一定的超調。

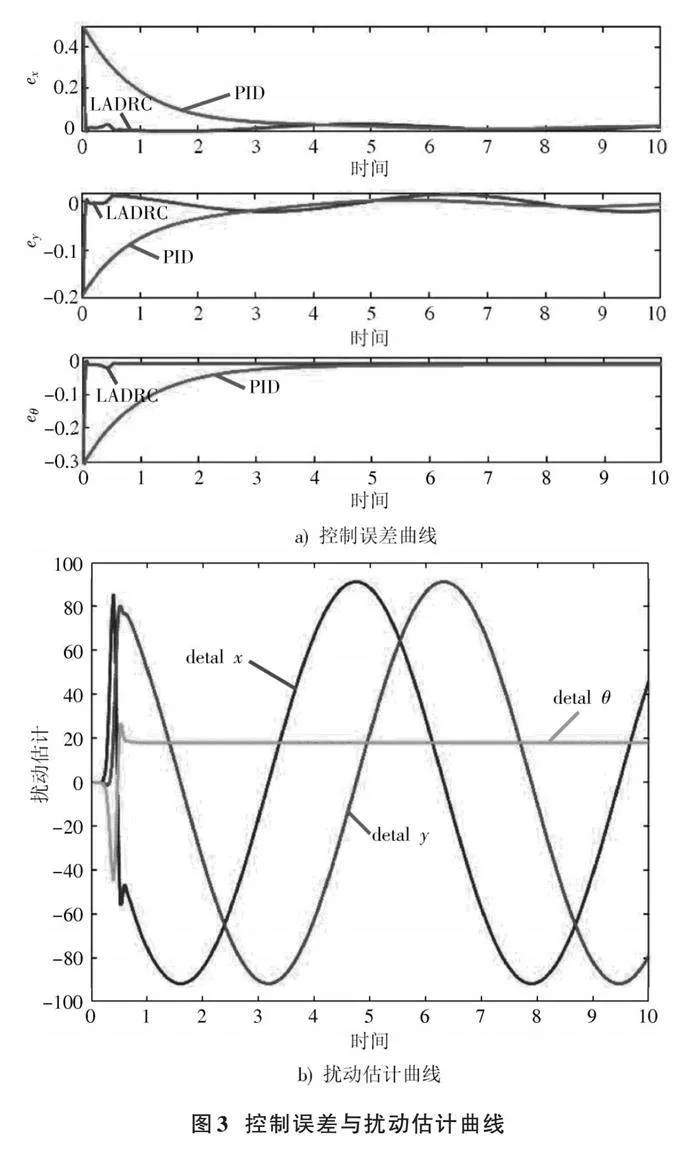
控制誤差與擾動估計曲線如圖3所示。由圖3a）可知，軌跡跟蹤過程中LADRC算法的控制性能明顯好于PID算法，優勢體現在如下兩個方面：

1） 控制性能較好。起始階段LADRC算法最大偏差小，系統到達穩態時間短，響應時間較快，控制誤差在穩定狀態下系統偏差較小，誤差波動很小，整個控制過程比較穩定。

2） 抗擾性能較好。LADRC算法響應迅速，跟蹤圓形軌跡的運動過程中沒有出現很大的偏差和抖振現象；而PID算法的控制誤差明顯較大，存在較大超調和振蕩，且軌跡跟蹤速度較慢。

由圖3b）可知，擾動作用過程中，觀測器的響應速度較快，LESO觀測器能夠快速精確地對擾動進行實時估計，使得控制器能夠對擾動進行實時補償，因此具有優越的主動抗干擾性能。另一方面，盡管LADRC的擾動估計值波動較大，但控制誤差比較小，說明算法的擾動補償能力好，具備較強的擾動抑制作用。擾動估計值包括機器人未建模的部分，能夠提升控制器的控制系統總體精度。

4 "結 "論

本文所設計的含有擾動補償的四輪全向Mecanum輪機器人LADRC控制器不僅能夠精確地獲得控制系統總擾動的估計值，并對其擾動進行補償，而且還能保證很高的控制精度，減小不確定性對機器人軌跡跟蹤控制的影響。同時本文設計的控制器保持了傳統LADRC的強魯棒性，控制性能不隨外界環境和擾動變化而變化，使得在實際軌跡跟蹤控制過程中機器人可以不受環境等因素限制，最大超調量可忽略不計，控制量輸出相對穩定，具有實際應用價值，有助于提升控制系統的穩定性和可靠性。本文研究的成果對于移動機器人技術的發展和應用具有重要意義。通過引入LADRC技術，成功提升了移動機器人的運動控制性能，使其更適應復雜和不確定的工作環境；同時，為移動機器人運動控制領域的進一步研究和應用提供了有益的參考和借鑒。

注：本文通訊作者為吳濤。

參考文獻

[1] 曹風魁，莊嚴，閆飛，等.移動機器人長期自主環境適應研究進展和展望[J].自動化學報，2020，46（2）：205?221.

[2] 謝嘉，桑成松，王世明，等.智能跟隨移動機器人的研究與應用前景綜述[J].制造業自動化，2020，42（10）：49?55.

[3] 張守武，王恒，陳鵬，等.神經網絡在無人駕駛車輛運動控制中的應用綜述[J].工程科學學報，2022，44（2）：235?243.

[4] SUN X， XIONG Y， YAO M， et al. A unified control method combined with improved TSF and LADRC for SRMs using modified grey wolf optimization algorithm [J]. ISA transactions， 2022， 131： 662?671.

[5] 翁發祿，郭毅，李勝飛.基于IBS和LADRC的四旋翼飛行器軌跡跟蹤控制[J].電光與控制，2019，26（6）：65?69.

[6] 田運陽，宋保業，吳尤，等.基于改進LADRC的全向移動機器人軌跡跟蹤控制[J].控制工程：1?8[2023?05?30].https：//doi.org/10.14107/j.cnki.kzgc.20220611.

[7] 王會明，張揚，王雪闖.移動機器人的線性自抗擾控制設計與實驗驗證[J].控制理論與應用，2022，39（7）：1289?1296.

[8] 王鑫，劉怡明，王明明，等.基于改進模糊PID的輪式機器人速度控制器設計[J].河北科技大學學報，2020，41（1）：50?57.

[9] PEZZATO C， FERRARI R， CORBATO C H. A novel adaptive controller for robot manipulators based on active inference [J]. IEEE robotics and automation letters， 2020， 5（2）： 2973?2980.

[10] LI Y， GE S， DAI S， et al. Kinematic modeling of a combined system of multiple mecanum?wheeled robots with velocity compensation [J]. Sensors， 2019， 20（1）： 75.

[11] 顧萬里，王萍，胡云峰，等.具有H_∞性能的輪式移動機器人非線性控制器設計[J].吉林大學學報（工學版），2018，48（6）：1811?1819.

[12] 何妍穎，李曄卓，武建昫，等.多模式兩輪移動機器人的設計與運動分析[J].機械工程學報，2019，55（23）：83?92.

[13] AJEIL F H， IBRAHEEM I K， AZAR A T， et al. Autonomous navigation and obstacle avoidance of an omnidirectional mobile robot using swarm optimization and sensors deployment [J]. International journal of advanced robotic systems， 2020， 17（3）： 1729881420929498.

[14] 趙珈靚.基于自抗擾控制的全方位移動機器人軌跡跟蹤研究[D].天津：天津大學，2018.

[15] WANG Hongdu， LI Xiaogang， LIU Xin， et al. Fuzzy sliding mode active disturbance rejection control of an autonomous underwater vehicle?manipulator system [J]. Journal of Ocean University of China， 2020， 19（5）： 1081?1093.

[16] 馬書根，趙珈靚，任超.基于無源性的全方位移動機器人自抗擾控制[J].控制與決策，2018，33（6）：1081?1086.