落實“四翼”考查要求助力創新人才選拔

[摘 要] 2024年高考數學新課標卷依托高考評價體系，創新試卷結構設計，深化基礎性考查，突出思維能力考查，強調對學科基礎知識、基本方法的深刻理解，繼續在反套路、反機械刷題上下功夫，創新人才選拔，引導教師轉變教學重點，從解題技巧總結轉向學科核心素養培養.

[關鍵詞] 2024年高考;新課標卷;命題風格;試題評析

高考評價體系中的“四翼”考查要求立足素質教育應達成的內容表現與形式表現，是高考對素質教育進行評價的基本維度[1]. 2024年高考數學新課標Ⅰ卷和Ⅱ卷繼續在反套路、反機械刷題上下功夫，強調對基礎知識和基本概念的深入理解和靈活掌握，注重考查學科知識的綜合應用能力，落實中國高考評價體系中“四翼”的考查要求. 命題可歸納為三個“堅持”：堅持素養導向，緊扣時代發展，設置真實的問題情境，引導學生將知識學習與實踐應用相結合，在解決實際問題的過程中發展核心素養;堅持考教銜接，依據新課標設計命題內容，注重考查學生對基礎知識、基本技能、基本思想方法的理解和掌握，打牢發展的根基;堅持面向未來，聚焦高校人才選拔要求，加強思維品質考查，體現基礎性、綜合性、應用性和創新性的考查要求，服務拔尖創新人才自主培養.

試卷整體風格的變化

（1）從卷面風格來看，新課標卷試題從往年的22道減至今年的19道，其中多選題、填空題和解答題各減少1題. 在考試時間不變的情況下，減少試題數量是強化思維考查的必要措施. 數學高考一直強調“多想一點，少算一點”的理念，減少試題數量能夠增加學生思考時間，考查學生的思考方式和過程，讓思維能力較強的學生展現素養，發揮潛力，脫穎而出.

（2）從考點布局來看，由于試題數量減少了，因此考查的知識內容的覆蓋面受到了一定影響. 新課標卷打破了以往的命題模式，靈活、科學地確定試題內容和順序，不受限于對某些具體知識內容的考查. 靈活改變試題順序有助于打破機械應試套路，以及教學中僵化、刻板的訓練模式，防止猜題押題，消除應試教育的弊端. 如新課標Ⅱ卷，函數題曾作為壓軸題，現調整為解答題的第2題;概率與統計題加大了能力考查力度，安排在解答題的倒數第2題.又如新課標Ⅰ卷，將解析幾何題安排在解答題的第2題，數列知識則結合新情境安排在壓軸題的位置.

（3）從命題意圖來看，《深化新時代教育評價改革總體方案》對中高考命題提出了明確要求：改變相對固化的試題形式，增強試題開放性，減少死記硬背和機械刷題現象. 也就是說，高考命題必須更靈活，去模式化. 新課標卷根據試卷結構調整后整卷題量減少的客觀情況，提高了最后兩道壓軸題的分值，創新能力考查策略，提升了壓軸題的思維量，突出理性思維和科學探究，把考查重點放在學生的思維品質和綜合應用能力上，不斷完善人才選拔標準和方式方法，服務高校招生和人才培養改革.

試題呈現特點的變化

1. 強化基礎性要求，注重學習過程

基礎性包括學科內容的基本性和通用性，深化基礎性就是加強對基本概念、基本原理、基本思想方法的考查，引導學生重視基礎，將所學的知識、思想方法內化為能力和素養[2]. 新課標卷命題遵循教育規律，注重考查學生對基礎知識、基本技能、基本思想方法的理解，強調在理解的基礎上融會貫通、靈活應用，避免死記硬背，引導中學教學回歸課標和課堂，重視概念教學，夯實學生學習基礎，把教學重點從解題技巧總結轉向學科核心素養培養.

例1 （新課標Ⅰ卷第12題）設雙曲線C：-=1（a>0，b>0）的左、右焦點分別為F，F，過F作平行于y軸的直線交C于A，B兩點. 若FA=13，AB=10，則C的離心率為________.

評析 由雙曲線的定義可知，2a=AF-AF=13-5=8. 又由勾股定理可知，2c=FF==12. 所以離心率e==. 應用雙曲線的定義和性質求解，可以避免較為復雜的坐標計算，從而有效地減少計算量，節省考試時間.

例2 （新課標Ⅱ卷第8題）設函數f（x）=（x+a）ln（x+b），若f（x）≥0，則a2+b2的最小值為（ ）

A. B. C. D. 1

評析 此題的函數模型簡單、基本，要求學生推斷兩個參數平方和的最小值. 由f（x）≥0可知，ln（x+b）與（x+a）始終同號. 當ln（x+b）=0時，考慮x+a=0，所以1-b=-a，即b=1+a. 所以a2+b2=a2+（a+1）2=2a++≥，當且僅當a= -，b=時取等號. 通過分析函數的單調性和函數的零點直接得到答案，不需要求導，不需要分類討論. 用創新設計考查學生真實的數學能力，而非刷題和訓練的技巧.

例3 （新課標Ⅰ卷第16題）已知A（0，3）和P3，為橢圓C：+=1（a>b>0）上兩點.

（1）求C的離心率;

（2）若過P的直線l交C于另一點B，且△ABP的面積為9，求l的方程.

評析 易求得橢圓C：+=1. 因為S=×3×3=，所以S△ABP=2S△AOP. 由橢圓的對稱性可設D（0，-3），連接PD，延長PO交橢圓C于點E，連接AE，則E-3，-，從而S△ADP=2S△AOP=9，S△AEP=2S△AOP=9，即當點B在點D和E時，△ABP的面積為9.

因為AP=，所以橢圓C上點B到直線AP的距離為. 所以滿足題意的點B最多只有兩個（點D和點E）. 因為k=，所以直線PD的方程為y=x-3，即3x-2y-6=0. 因為k=，直線PE的方程為y=x，即x-2y=0. 所以直線l的方程為3x-2y-6=0和x-2y=0.

此解法利用圖形面積關系，源于對圖形特征的“敏感”，平和中有新意，靈活中見潛力. 其他解法諸如設點B的坐標，以AP為底，點B到AP的距離為高表示△ABP的面積后解方程，計算量相對較大.

2. 彰顯綜合性要求，回歸數學本質

在知識交匯點設問，考查知識間的內在聯系，體現知識的綜合性. 這種命題方式鼓勵學生跨領域思考，建立知識點間的聯系，建構完整的知識體系和網絡結構，形成新的認識和解題思路，達到融會貫通和深度理解知識的目標.

例4 （新課標Ⅰ卷第5題）已知圓柱和圓錐的底面半徑相等，側面積相等，且它們的高均為，則圓錐的體積為（ ）

A. 2π B. 3π

C. 6π D. 9π

評析 由側面積相等得2πr·=πr·，解得r=3，故圓錐的體積為V=πr2·=3π. 此題考查學生對高與母線概念的辨析，對圓柱與圓錐的側面積公式的區分，以及對圓錐的體積公式的應用.

例5 （新課標Ⅱ卷第6題）設函數f（x）=a（x+1）2-1，g（x）=cosx+2ax（a為常數），當x∈（-1，1）時，曲線y=f（x）和y=g（x）恰有一個交點，則a=（ ）

A. -1 B. C. 1 D. 2

評析 設h（x）=f（x）-g（x），曲線y=f（x）和y=g（x）恰有一個交點等價于函數y=h（x）有唯一零點. 又h（x）=ax2+a-1-cosx為偶函數，所以h（0）=0，解得a=2. 此題綜合考查冪函數和余弦函數的性質、函數零點的概念，以及數形結合思想，沒有考查煩瑣的函數求導計算，要求學生在深入理解知識的同時，實現知識的融會貫通，而非局限于解題技巧.

例6 （新課標Ⅱ卷第19題）已知雙曲線C：x2-y2=m（m>0），點P（5，4）在C上，k為常數，0<k<1. 按照如下方式依次構造點P（n=2，3，…）：過點P作斜率為k的直線與C的左支交于點Q，令P為Q關于y軸的對稱點，記P的坐標為（x，y）.

（1）若k=，求x，y;

（2）證明：數列{x-y}是公比為的等比數列;

（3）設S為△PnPn+1Pn+2的面積，證明：對于任意正整數n，S=S.

評析 此題融合解析幾何和數列，分層設問，環環相扣. 三個小問利用基本方法可以大幅簡化計算過程：第（2）問利用固定斜率直線與雙曲線交點性質，可迅速得到結論;第（3）問可以將證明面積相等轉化為證明兩條直線平行.

（1）因為點P（5，4）在C上，所以m=x2-y2=52-42=9. 所以雙曲線C：x2-y2=9. 又Q（-x，y），當k=時，有x-y=9，y-4=（-x-5），解得x=3y=0 或x=-5y=4（舍去）. 所以x=3，y=0.

（2）由題意得P（x，y），Q（-x，y），直線PnQn的斜率為k. 設Z=x-y，由x-y=9，x-y=9相減得=1. 又k=，所以y-y=-k（x+x），x-x=-k（y+y）.兩式相減得Z-Z=k（Z+Z），所以=. 故數列x-y是公比為的等比數列.

（3）要證S=S，即證S=S，只需證PP∥PP.設=q，由（2）可知x-y=qn-1，x+y=9·，所以x=qn-1+9·，y=·-qn-1.PP的斜率k===1-=1-=1-.

PnPn+3的斜率k′===1-=1-=1-.

所以k=k′，故PP∥PP.

3. 注重應用性要求，實現學科育人

試題突出素養導向，緊扣時代發展，設置真實的問題情境，引導學生將知識學習與實踐應用相結合，在解決實際問題的過程中發展核心素養. 數學從“解題”到“解決問題”的轉變已經成為當前數學教育的一個重要趨勢.這種轉變不僅有助于學生更好地理解和掌握數學知識，還能培養他們實踐能力和創新精神.

例7 （新課標Ⅱ卷第14題）在下圖（圖3）的4×4方格表中選4個方格，要求每行和每列均恰有一個方格被選中，則共有________種選法;在所有符合上述要求的選法中，選中方格中的4個數之和的最大值是________.

評析 每行和每列均恰有一個方格被選中，共有4×3×2×1=24種選法. 要使4個數之和最大，先看十位上的數，其和一定是10+20+30+40=100，再選個位上最大的數，其和為5+3+3+1=12，所以4個數之和的最大值是112.此題考查排列組合，是推理型分割問題，思維量大，體現多思少算，區分度佳.

例8 （新課標Ⅰ卷第14題）甲、乙兩人各有四張卡片，每張卡片上標有一個數字，甲的卡片上分別標有數字1，3，5，7，乙的卡片上分別標有數字2，4，6，8. 兩人進行四輪比賽，在每輪比賽中，兩人各自從自己持有的卡片中隨機選一張，比較所選卡片上數字的大小，數字大的人得1分，數字小的人得0分，然后各自棄置此輪所選的卡片（棄置的卡片在此后的輪次中不能使用），則四輪比賽后，甲的總得分不小于2的概率為________.

評析 表格或樹狀圖是分析排列組合問題常用的工具. 問題等價于從圖4①中的16個方格中任取4個，4個方格既不同行也不同列，求“1”的個數大于等于2的概率. 為了表述方便，現重新編號（如圖4②所示）.

①3個“1”的情況：C-B-A，1種.

②2個“1”的情況：C-B-A，1種;C-A-B/B，2種;C-A-B，1種;A-B-C/C，2種;A-B-C/C，2種;A-B-C/C，2種;A-B-C，1種.

合計共12種情況，所以甲的總得分不小于2的概率為P==.

本題考查學生的理性思維和探究能力，套路和模板失效，死記硬背不再適應高考新要求.

4. 突出創新性要求，助力人才選拔

試題強調創新，設計新穎情境和設問方式，加強基本能力考查，提升解答題思維量，強調理性思維和數學探究，考查學生運用數學思維和數學方法發現問題、分析問題和解決問題的能力，要求學生融合知識、經驗、方法，并遷移轉化運用，為全面發展奠定基礎.

例9 （新課標Ⅰ卷第11題）設計一條美麗的絲帶，其造型φ可以看作圖中的曲線C的一部分.已知C過坐標原點O，且C上的點滿足橫坐標大于-2，到點F（2，0）的距離與到定直線x=a（a<0）的距離之積為4，則（ ）

A. a=-2

B. 點（2，0）在C上

C. C在第一象限的點的縱坐標的最大值為1

D. 當點（x，y）在C上時，y≤

評析 由題意得曲線C的軌跡方程為·x-a=4，原點（0，0）在C上，所以a=2. 又a<0，故a=-2. 選項A正確. 因為·x+2=4，令y=0，解得x=0或2.選項B正確. 當x>0時，y2=-（x-2）2，令g（x）=-（x-2）2，顯然g（2）=1，且g′（2）<0，所以g（x）>g（2）=1. 選項C錯誤. 由y2=-（x-2）2≤得y≤=（x>-2）. 選項D正確. 故正確的選項有ABD.

此題背景為有理曲線，可由笛卡兒葉形線旋轉得到，常見的還有蔓葉線、馬利克曲線、環索線等有理曲線. 新定義試題屬于傳統開放性試題，實質是原認知結構與新知識之間的遷移. 解決此類問題的關鍵是讀懂題意，理解新定義，確定探究方向，運用類比與歸納的方法尋找合理的解題思路.

例10 （新課標Ⅰ卷第19題）設m為正整數，數列a，a，…，a是公差不為0的等差數列，若從中刪去兩項a和a（i<j）后剩余的4m項可被平均分為m組，且每組的4個數都能構成等差數列，則稱數列a，a，…，a是（i，j）—可分數列.

（1）寫出所有的（i，j），1≤i≤j≤6，使數列a，a，…，a是（i，j）—可分數列.

（2）當m≥3時，證明：數列a，a，…，a是（2，13）—可分數列.

（3）從1，2，…，4m+2中一次任取兩個數i和j（i<j），記數列a，a，…，a是（i，j）—可分數列的概率為P，證明：P>.

評析 此題以等差數列為知識背景，創新設問方式，設置數學新定義，搭建思維平臺，引導學生積極思考，在思考過程中領悟數學方法，自主選擇路徑和策略分析問題、解決問題. 第（1）問和第（2）問根據題意容易解決，同時為第（3）問提供了解決思路.

對于第（3）問，其基本事件的總數為C. 受第（1）問和第（2）問的啟發，分兩種情況：

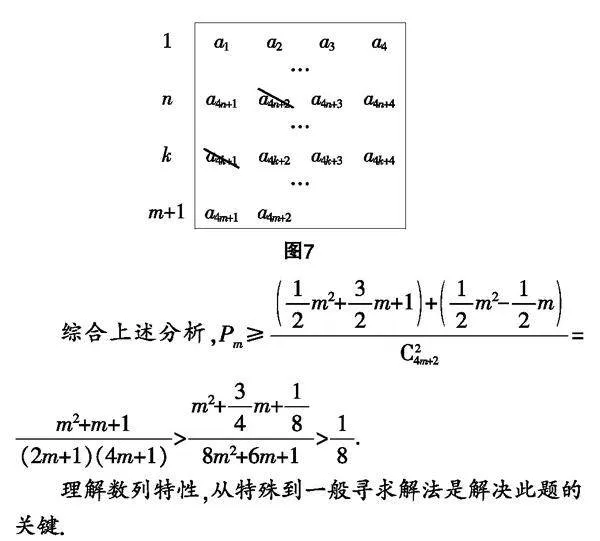
第一，如圖6所示，刪除第4n+1和4k+2項，其中0≤n≤k≤m+1. 此時前4n項、中4（k-n）項、后4（m-k）項按原順序4項一組都能構成等差數列，即（4n+1，4k+1）—可分數列.

當n=k時，這樣的（n，k）有m+1組;當n<k時，這樣的（n，k）有C組. 因此，滿足條件的（n，k）共有m+1+C=m2+m+1組.

第二，如圖7所示，刪除第4n+2和4k+1項，其中0≤n≤k≤m+1，k-n≥2. 此時前4n項、后4（m-k）項按原順序4項一組都能構成等差數列，中間4（k-n）項同樣可構成等差數列，即（4n+2，4k+1）—可分數列.這樣的（n，k）共有（m-1）+（m-2）+…+1=m2-m組.

綜合上述分析，P≥=>>.

理解數列特性，從特殊到一般尋求解法是解決此題的關鍵.

2024年高考綜合改革適應性測試卷公布后，各地模擬卷充斥著以高等數學為背景的新定義壓軸題，試圖通過超綱知識投機取巧，這顯然不符合高考命題改革要求. 壓軸題考查的并非學生的“知識量”，而是其“思維量”. 教師應著重培養學生的思維能力、探究能力和解決問題能力，避免超綱學、超量學，引導學生獨立思考和深度學習.

結束語

2024年高考數學新課標卷嚴格依據高中課程標準，通過命題創新，提高試題靈活度，豐富試卷內容與形式，優化試卷結構，突出考查學生的理性思維和探究能力，切實改變機械刷題和套路訓練的現象，強調學生的思維過程，積極引導教學回歸育人本位，發揮正向積極的導向作用. 高考改革后，機械刷題和套路訓練已不合時宜，無法滿足新高考對關鍵能力和學科素養的考查需求. 新課標卷打破了固化的應試思維，引導教學重視情境創設，關注知識的生成過程，引導學生通過觀察、思考、探究構建認知結構，提高學生發現問題、提出問題、分析問題和解決問題的能力;引導教學關注思維深刻性，在學生掌握“四基”后，通過問題引導和深化提升，促進學生思考，實現從“學科知識”到“學科育人”的轉變.

參考文獻：

[1] 教育部考試中心. 中國高考評價體系（2019年版）[M]. 北京：人民教育出版社，2019.

[2] 翟嘉祺，任子朝，趙軒. 高考深化基礎性考查研究[J]. 中學數學教學參考，2022（31）：4-7.

作者簡介：雷波（1981—），中學數學高級教師，主要從事中學數學教育教學工作.