留白:讓學生的思維向深處漫溯
【摘要】“留白”是書畫創作中的一種技法,數學教學與中國書畫創作有相通之處,應借鑒書畫創作中的留白,給學生一定的思考時間與空間,讓學生自由探索,成為學習的主人.教師可在導入新課、探求新知、練習環節中適度留白,以激發學生興趣,發展學生思維,進而提升學生的核心素養.
【關鍵詞】留白;核心素養;初中數學
“留白”是書畫創作中的一種技法,即在書畫作品中留出一定空白不著墨跡,旨在給欣賞者以一定的遐想.傳統教學中,數學教學更多依賴于教師的講解,給學生獨立思考的時間比較少.數學是思維的體操,沒有個人思維的參與,數學教學效果甚微.其實,數學教學與中國書畫創作有相通之處,應借鑒書畫創作中的留白,給學生一定的思考時間與空間,讓學生自由探索,成為學習的主人.這就需要教師在設計留白時,必須深入研讀教材,準確把握學情,架設好教師的“講”與學生的“學”之間的橋梁,它是教學節奏中“張”與“馳”之間的銜接點.需要注意的是,留白并非放任自由,也不可頻繁使用,如果留白過多,教學會顯得松松垮垮,那么,如何留白才能恰到好處,達到實效呢?
1 留白的理論基礎
格式塔心理學派的“完形壓強”理論認為,人類通過感官知覺得到的是一個完整的形象,如果遇到了不完美或殘缺的圖形或事物時,會不自覺產生補缺的想法,以求得內心的平衡.根據上述心理學的理論,教學中設計一定的留白,給學生創造不完滿的情境,就會對學生的大腦形成一種刺激,從而激發學生大腦的思維活動,去填補其中的缺憾,促使學生去思考和探究.
建構主義理論認為,學習不能讓學生被動地接受知識,而應讓學生自主建構.即教學中應以學生為主體,教師為指導,教師與學生要在交流互動中共同推進教學,培養學生自主學習的能力.有了建構主義學習理論,數學教學就有了方法論,要給學生時間與空間,讓學生去思考與學習,進而促進學生的個性化發展,這樣的課堂是民主的、開放的.
2 留白的路徑探尋
2.1 導入新課時留白,激發學生興趣
課堂導入關系到本節課的起始點與課堂知識的產生.如何把學生的注意點吸引到數學課堂上?教師不能直接將結論告知學生,要以引入知識為時機,給學生設計留白,留下懸念,使學生處于“心求通而未達,口欲言而未能”的狀態,進而調動學生的學習興趣,激起學生的思考.
例如 “一元一次方程”的教學節選
情境 一輛客車和一輛卡車同時從A地出發沿同一公路同方向行駛,客車的行駛速度是60千米/小時,卡車的行駛速度是40千米/小時,客車比卡車早2小時經過B地,A、B兩地間的路程是多少千米?
學生 當A、B兩地間的路程是120千米時,客車需要2小時,卡車需要3小時,客車比卡車早到1小時;當A、B兩間的路程是240千米時,客車需要4小時,卡車需要6小時,客車比卡車早到2小時,所以A、B兩地間的路程是240千米?
教師 這位同學用列舉的方法得到了結果,用方程的方法如何解呢?
學生 設A、B兩地間的路程為x千米, 根據題意,得x40-x60=2.
教師 這就是我們本章即將要學習的一元一次方程,如何解這個方程求出x的值呢?
……
通過行程問題中求兩地間距離的情境,引出了一元一次方程,但是方程能列出來,如何解這個方程呢?給學生留下了一定的空白,初步感受實際生活中的數量關系可以用一元一次方程來描述,體會一元一次方程的價值,為后期進一步解方程奠定基礎.
2.2 探求新知時留白,喚激情
學習是自主建構的過程,在探究知識的過程中完成對知識的理解.然而,學生的認知結構的形成過程是螺旋式上升的.教師在引導過程中要在知識的關鍵之處留白,要突出數學的本質,使學生在親歷探究中,建立正確的認知.
2.2.1 在提問后留白
思維的建立需要經過一個過程.因此,教師在提出問題后不能急于讓學生回答,不要以課堂45分鐘時間寶貴為理由,為防止學生的奇思異想打亂教學計劃,而不給學生思考的時間,這會在無形中降低教師提出的問題的價值,也不能培養學生的思維能力.在教師提問后,要有所停頓,適當的留白,給學生留下一定的時間和空間,培養學生發現問題、提出問題與解決問題的能力,變教師的精講為學生的精思,切實提高課堂效率.
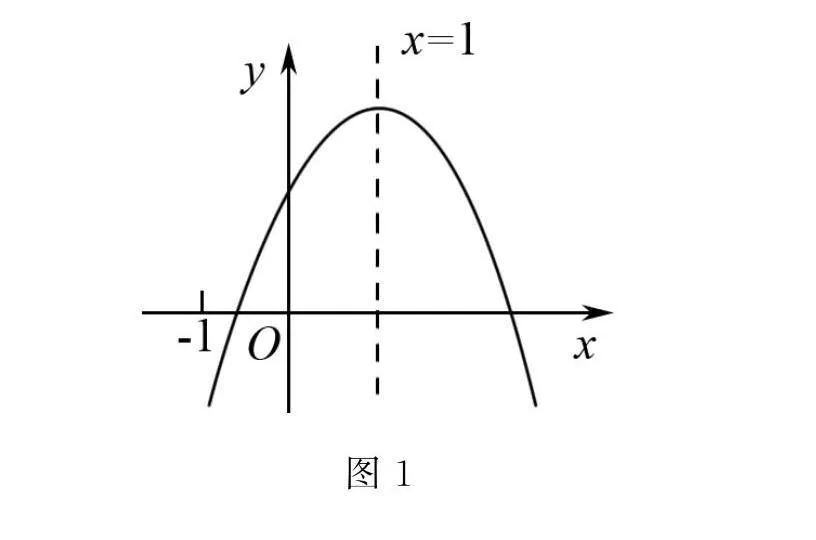
例如 在復習“二次函數圖象與系數關系”一課中,筆者采用了層層遞進,不斷深入的方式,引導學生思維走進數學抽象的思維中.已知二次函數y=ax2+bx+c(a≠0)的圖象如圖1所示.
問題1:如圖1所示,如何根據圖象在坐標系中的位置求出字母a、b、c的正負號呢?問題2:如圖所示,如何根據二次函數圖象對稱軸的位置求得2a-b的正負號呢?問題3:如圖所示,如何得到代數式9a+3b+c,并求出它的正負號呢?問題4:根據上面的研究成果,如何比較c與-3a的大小關系呢?問題5:根據問題4的活動經驗,如何比較a+b與am2+bm的大小關系呢?
上面五個問題從舊知到新知,從簡單到復雜,逐步把學生的思維引向深入,學生的狀態處于主動、自主的狀態,思維不斷向深處漫溯,教學效果令人滿意.
2.2.2 在重難點處留白
影響課堂教學效果的因素著重取決于教師對本節課重難點的把握和突破程度,有不少教師埋怨學生:“我這道題講了三四遍,并強調這是重要知識,但是你們為什么還要做錯呢?”實際上在本節課的重難點之處,不是教師強調這是重難點,學生就一定會掌握的,而適當留白,并適當停頓,設計一些前置性問題,讓學生先自主探究,在反思中加深學生對于知識的理解與掌握.
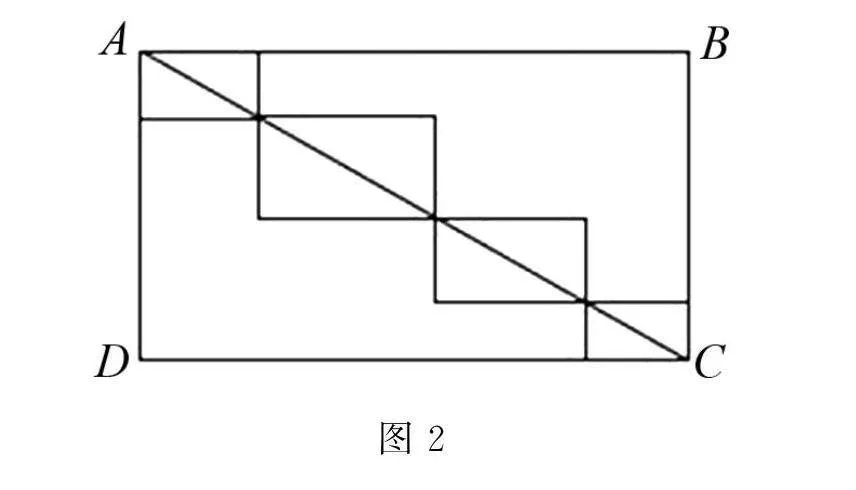
例如 如圖2所示,正方形ABCD的邊長為5,把它的對角線AC分成n小段,以每一小段為對角線作一個小正方形,那么這n個小正方形的周長之和為多少呢?
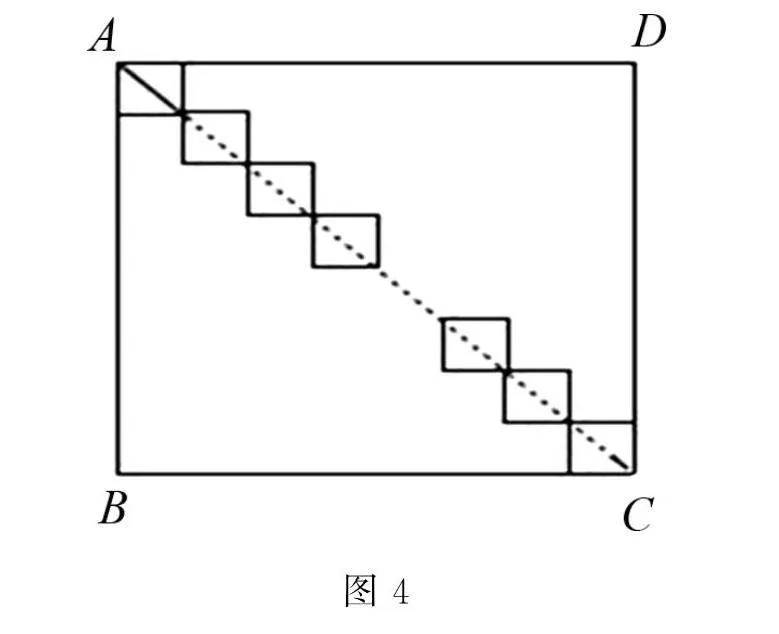
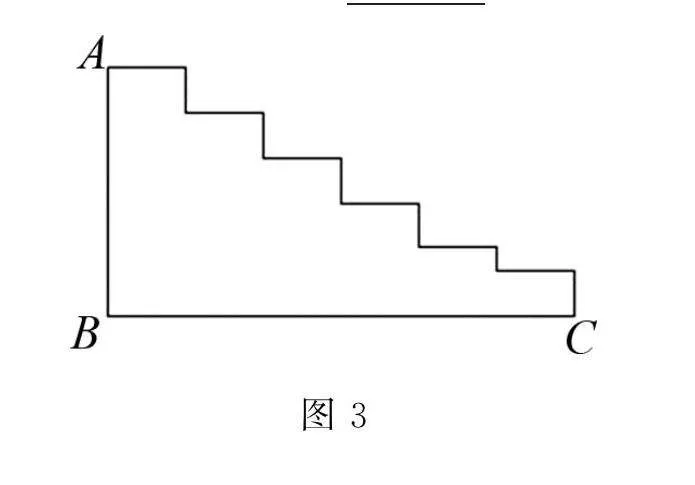
此題考查的是學生能否利用平移解決問題,筆者發現學生對這一問題有困難,為此,筆者提前設置了下面幾個前置問題:(1)如圖3所示,對于如何求臺階的總長,小紅的辦法是量出每階臺階的高度與寬度,然后加起來,小剛的辦法是只需量出臺階的高AB和長CD的長,你認為小剛的辦法可以嗎?(2)如圖4在長方形ABCD中,AB=11,BC=5,則圖中四個小長方形的周長和為 .
教學中,教師把知識全部掰開喂給學生,就剝奪了學生思考的權力.因此,教師設計一些有思考價值的問題,給學生留下感興趣的空白,激起學生強烈的認知沖突,點燃學生參與課堂教學的熱情,在自主探究中,實現重難點問題的突破.
2.2.3 練習中留白,拓展學生思維
在數學教學中,練習起著鞏固新知的重要作用,所以教師要在練習中留白,設計的練習要具有層次性、開放性,給學生更多的探索空間,把學生的思維引向更廣闊的天地,它對于拓展學生的思維具有重要作用.
在傳統教學中,教師布置作業都是統一的,學生沒有拓展的空間.筆者嘗試給學生安排了“作業超市”.在作業超市里,有基礎題,補差型試題、能力拔高題,學生可以根據自己不同的學習基礎,根據對于新知的掌握情況,選擇適合自己的作業,一方面提高了學生的選擇能力,也開發了學生的潛力,讓學生得到最優的發展.
基礎性試題:根據當天學習的新知命題,考查知識點為每一個知識點及重點.
補差型試題:對于學習基礎不扎實的同學,要布置一些淺顯易懂的,讓他們也獲得成功的快樂,培養這部分學生的自信心.
能力拓展題:對于學有余力的同學,要設計一些有一定難度,且綜合性比較強的試題,可以培養學生思維的深刻性與靈活性.
通過基礎性試題、補差型試題、拓展型試題,教師可以及時了解學生對于已學知識的掌握情況,并可以根據學生情況調節教學,進而使后期教學更具有針對性,進而提高課堂實效.
3 結語
總之,留白是一種藝術.教學中,教師應在新課導入處,探求新知處、課后練習處進行精心設置留白,以激發學生興趣,發展學生思維,進而提升學生的核心素養.
參考文獻:
[1]陳秀海.幽默引人入勝留白發人深省結語繞梁三日——初中數學課堂教學語言藝術提升研究[J].中學數學,2023(24):88-89.
[2]徐建國.融創課堂理念下的初中數學課堂留白[J].數學教學通訊,2022(23):47-48.
[3]楊峰.初中數學課堂留白三策略[J].現代中學生(初中版),2021(06):5-6.
[4]趙麗.初中數學課堂留白的教學研究[D].重慶:西南大學,2021.

