在思考中探索 在拓展中創新

【摘要】解題能力的培養需要教師在課堂教學中通過思考、探究,延伸知識點,拓展解題思路以及創新解題等方式深挖相關的例題,引導學生進行科學有序的訓練.本文通過探究幾個數學例題,論述解題能力培養的重要性,幫助學生從例題中發現更深層次的規律和思維方法,培養學生的邏輯思維、分析問題的能力,并促進他們的創新思維能力得到發展.
【關鍵詞】初中數學;解題能力;探究;創新
中考是評價學生數學水平的重要考試,教師需要指導學生運用解題思路解決各種類型的數學問題.而數學中的經典例題需要進行思考并探索其考查的知識點,進而形成系統的知識框架.如果只是停留在例題表面,可能會陷入“模式化思維”,因此需要對這些例題進行革新與拓展,從而促進學生的思維發展,提高學生的綜合素養和解題能力.即通過對例題進行更深層次的探索和研究,將其進行拓展與創新,可以激發學生的思維,增強他們的解題能力.從不同的角度來解題,培養學生靈活運用知識的能力,使他們能夠更好地理解和應用數學概念,提高他們解決問題和應對挑戰的能力.
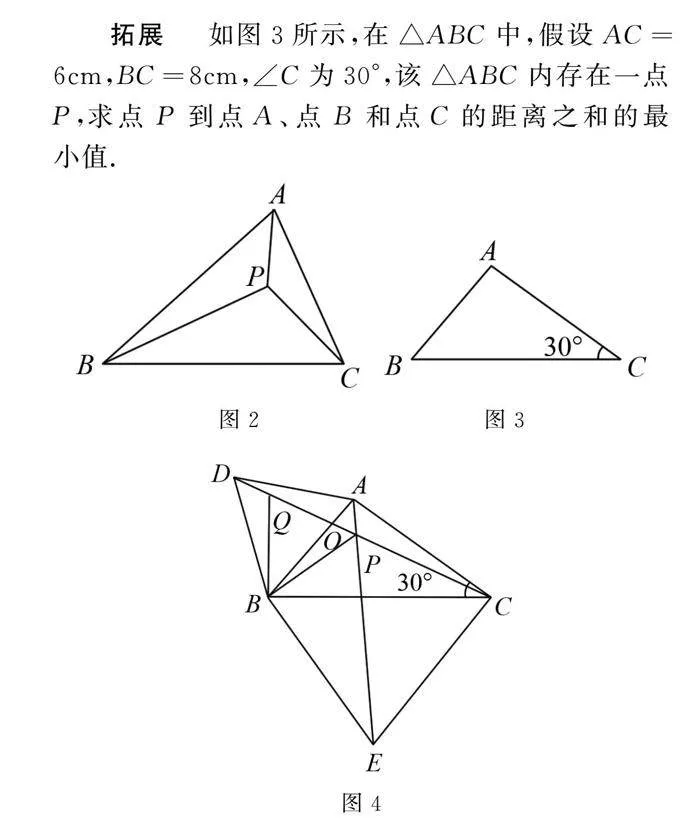
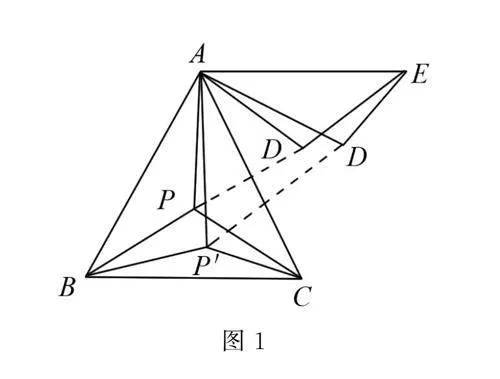
例1 如圖1所示,點P為等邊三角形ABC的中心,△ADE與△ACP全等,∠PAD=60°,連接PD,可得PD=PA,由此可知△APD為等邊三角形,則∠BPD=180°,∠PDE=180°,那么點E、點D、點P和點B在一條直線上,因此PA,PB和PC之和等于PD,PB和DE之和,且數值上等于BE.在△ABC中,取一點P′,該點到點A、點B和點C的連線所形成的夾角固然是不相等,那么點B、點P′、點D′和點E不在一條直線上,所以P′A,P′B和P′C之和大于PA,PB和PC之和,即點P到點A、點B和點C的距離之和最小.
探究 如圖2所示,P在△ABC中,∠APB,∠BPC和∠APC相等,證明點P到點A、點B和點C的距離之和最小.
拓展 如圖3所示,在△ABC中,假設AC=6cm,BC=8cm,∠C為30°,該△ABC內存在一點P,求點P到點A、點B和點C的距離之和的最小值.
分析 探究題是例1的一個問題的轉化,同樣是點P到三角形頂點的距離問題,以例1為啟示進行拓展,如圖4所示,分別以AB,BC為邊向外作等邊三角形,同樣連接CD,AE交于點P,進而證明△ABE與△DBC全等,可得CD=AE,∠BAE=∠BDC,在DO上取一點Q,使DQ=AP,則△ABP和△DBQ全等,故可證得△PBQ為等邊三角形,那么PB=PQ,可得點P到點A、點B和點C的距離之和等于DQ,PQ和PC之和,且與CD,AE相等,再根據勾股定理便可算出AE.
變式1 如圖5所示,∠ACB=∠CBA=∠DCE=∠CED = 60°,點A,點D和點E這3點共線,連接BE.
①∠AEB的度數為60°;
②線段AD,BE之間的數量關系為AD = BE.
變式2 如圖6所示,AC=BC,DC=CE且∠ACB和∠DCE均為直角,點A、點D和點E三點共線,過C點作△DCE的高CM與DE相交于點M,連接BE,求∠AEB的度數以及CM,AE,BE的關系.
yXm8Jh8rYCc2C0nSvZNtLxgSaIHpZyXiF+7N8PmYyGk=分析 變式1:根據題意可知△ACB和△DCE均為等邊三角形,△ACD和△BCE全等,進而可知AD=BE,∠ADC=∠BEC.點A,點D和點E這3點共線能夠求出∠ADC,進而∠AEB的度數便可求出.
變式2:根據變式1中的解法可求出∠AEB以及AD = BE;由題意可知△ABC和△DCE均為等腰直角三角形,可得CM =DM = ME,進而求出CM,AE,BE的關系為AE = 2CM +BE.
例2 如圖7所示,AB =10,∠B為60°,△ABC的邊AB和BC上存在點D和點E,BD = BE =4,△B′DE是通過△BDE沿DE翻折所得,將點A和點B′連接,試求AB′的長.
分析 在本題當中,關鍵點在于構造直角三角形,使用勾股定理尋求邊之間的關系,因此我們過點D作B′E的垂線交于點F,過點B′作AD的垂線交于點G,如圖8,∠B=60°,則△BDE為等邊三角形,且邊長等于4.△B′DE是通過翻折所得,故其也為等邊三角形,GD=B′F=2,B′D=4,由勾股定理可得:B′G= B′D2-GD2,進而計算可知B′G=23,則AB=10,即AG=10-6=4,最終可計算AB′的長度.
拓展 如圖9所示,四邊形ABCD為矩形,以GH為對折線折疊,點Q和點E分別為點C和點D的落點,EQ和BC交于點F,AD=8,AB=6,AE=4,試求△EBF的周長.
分析 該題與例2同為圖形的折疊,把握矩形的特性以及折疊過來之后圖形的關系,通過例2進行舉一反三即可求出△EBF的周長為8cm.
結語
初中數學解題能力培養可以通過對原題進行思考,探索其所考的知識點及系統的知識框架,通過拓展原題或者延伸相類似的知識點,去形成系統性和條理性的解題思路,使得解題思路更加靈活.本文以兩個幾何例題進行探究和分析,并對兩個例題進行拓展,進而培養學生的解題思路,使學生對問題有更深入的理解,能夠靈活應變地做一類題而不是某一道題.此外,通過在思考中探索、在拓展中創新的方式培養數學解題能力,增強學生的問題意識和探索精神,培養學習興趣和自信心,為他們的數學學習和綜合素質發展奠定堅實基礎,并為未來的學習和職業發展打下良好基礎.
參考文獻:
[1]孔婷薇.初中數學學生解題能力的培養研究[J].數學學習與研究,2023(08):146-148.
[2]李權生.初中數學教學中如何培養學生的解題能力[J].新課程,2022(11):156-157.
[3]阮準.初中數學解題反思能力的培養[J].數理化解題研究,2022(26):41-43.

