平面圖形與立體圖形之間的轉化關系
【摘要】本文深入研究了平面圖形與立體圖形之間的轉化關系,探討了從不同角度觀察、展開、折疊和旋轉等幾個方面的具體問題.通過這些問題的求解,得出了平面圖形和立體圖形之間獨特而豐富的關聯,為幾何學和圖形學領域提供了新的理解和認識.
【關鍵詞】平面圖形;立體圖形;轉化關系
1 從三個方向看,用平面圖形表示立體圖形
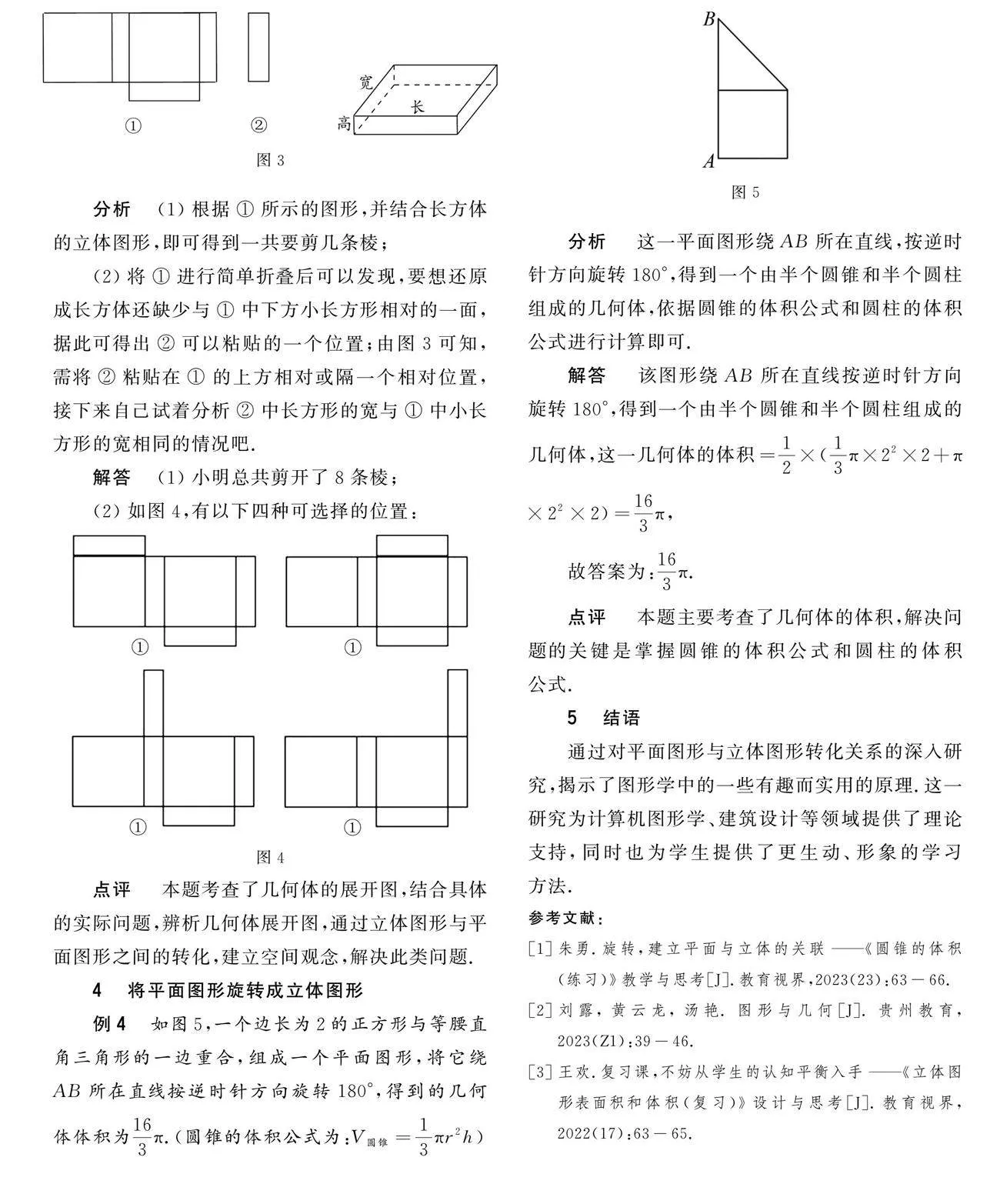
例1 由若干個完全相同的小正方體組成一個立體圖形,它的左視圖和俯視圖如圖1所示,則小正方體的個數不可能是( ).
(A)5. (B)6. (C)7. (D)8.
分析 直接利用左視圖以及俯視圖進而分析得出答案.
解答 由左視圖可得,第2層至少有一個小立方體,第1層一共有5個小立方體,故小正方體的個數最少為:6個,故小正方體的個數不可能是5個.故選(A).
點評 此題主要考查了由三視圖判斷幾何體,正確想象出所用正方體最少時的幾何體的形狀是解題關鍵.
2 將立體圖形展開為平面圖形
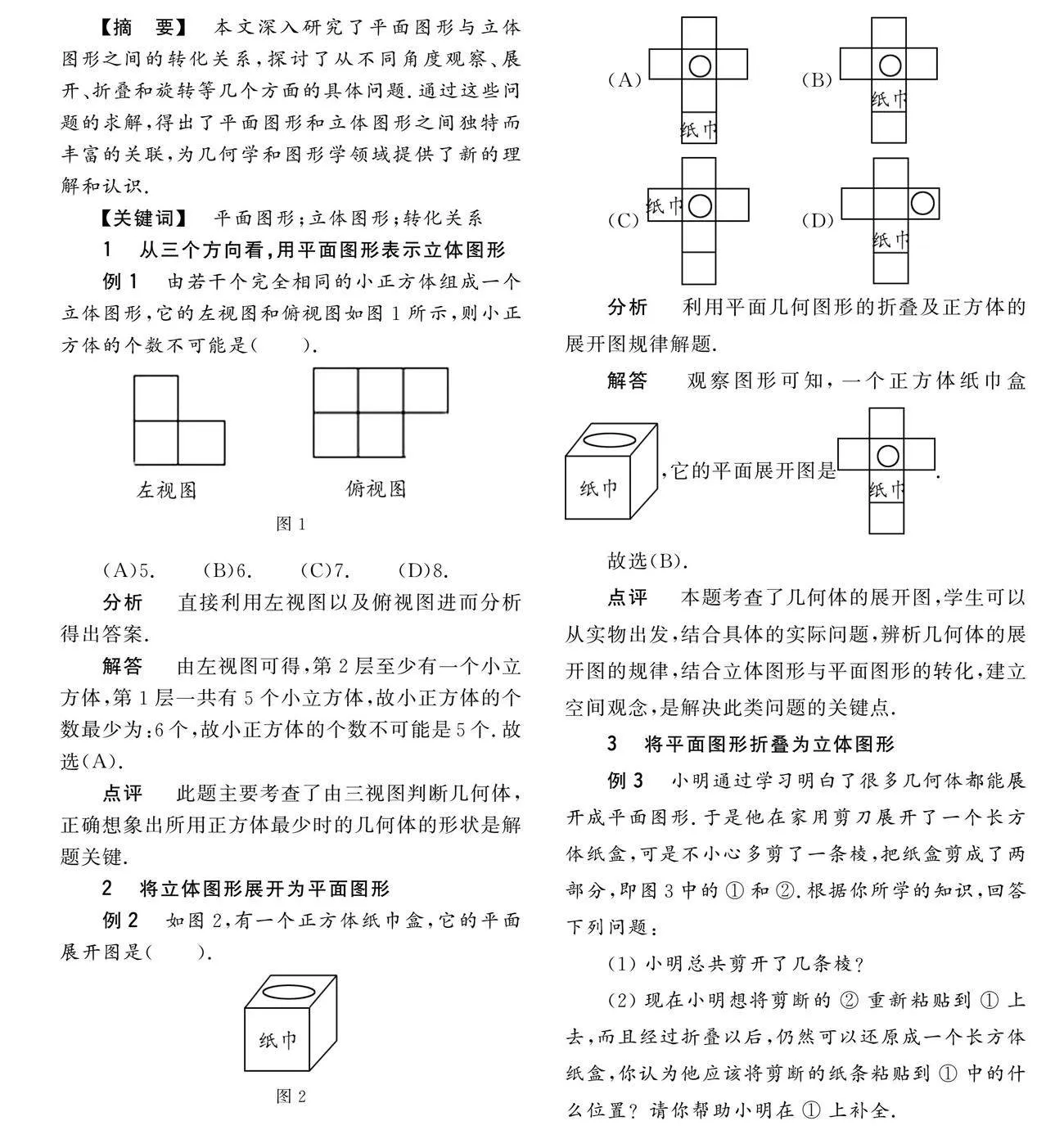
例2 如圖2,有一個正方體紙巾盒,它的平面展開圖是( ).
(A) (B)
(C)(D)
分析 利用平面幾何圖形的折疊及正方體的展開圖規律解題.
解答 觀察圖形可知,一個正方體紙巾盒,它的平面展開圖是.
故選(B).
點評 本題考查了幾何體的展開圖,學生可以從實物出發,結合具體的實際問題,辨析幾何體的展開圖的規律,結合立體圖形與平面圖形的轉化,建立空間觀念,是解決此類問題的關鍵點.
3 將平面圖形折疊為立體圖形
例3 小明通過學習明白了很多幾何體都能展開成平面圖形.于是他在家用剪刀展開了一個長方體紙盒,可是不小心多剪了一條棱,把紙盒剪成了兩部分,即圖3中的①和②.根據你所學的知識,回答下列問題:
(1)小明總共剪開了幾條棱?
(2)現在小明想將剪斷的②重新粘貼到①上去,而且經過折疊以后,仍然可以還原成一個長方體紙盒,你認為他應該將剪斷的紙條粘貼到①中的什么位置?請你幫助小明在①上補全.
分析 (1)根據①所示的圖形,并結合長方體的立體圖形,即可得到一共要剪幾條棱;
(2)將①進行簡單折疊后可以發現,要想還原成長方體還缺少與①中下方小長方形相對的一面,據此可得出②可以粘貼的一個位置;由圖3可知,需將②粘貼在①的上方相對或隔一個相對位置,接下來自己試著分析②中長方形的寬與①中小長方形的寬相同的情況吧.
解答 (1)小明總共剪開了8條棱;
(2)如圖4,有以下四種可選擇的位置:
點評 本題考查了幾何體的展開圖,結合具體的實際問題,辨析幾何體展開圖,通過立體圖形與平面圖形之間的轉化,建立空間觀念,解決此類問題.
4 將平面圖形旋轉成立體圖形
例4 如圖5,一個邊長為2的正方形與等腰直角三角形的一邊重合,組成一個平面圖形,將它繞AB所在直線按逆時針方向旋轉180°,得到的幾何體體積為163π.(圓錐的體積公式為:V圓錐=13πr2h)
分析 這一平面圖形繞AB所在直線,按逆時針方向旋轉180°,得到一個由半個圓錐和半個圓柱組成的幾何體,依據圓錐的體積公式和圓柱的體積公式進行計算即可.
解答 該圖形繞AB所在直線按逆時針方向旋轉180°,得到一個由半個圓錐和半個圓柱組成的幾何體,這一幾何體的體積=12×(13π×22×2+π×22×2)=163π,
故答案為:163π.
點評 本題主要考查了幾何體的體積,解決問題的關鍵是掌握圓錐的體積公式和圓柱的體積公式.
5 結語
通過對平面圖形與立體圖形轉化關系的深入研究,揭示了圖形學中的一些有趣而實用的原理.這一研究為計算機圖形學、建筑設計等領域提供了理論支持,同時也為學生提供了更生動、形象的學習方法.
參考文獻:
[1]朱勇.旋轉,建立平面與立體的關聯——《圓錐的體積(練習)》教學與思考[J].教育視界,2023(23):63-66.
[2]劉露,黃云龍,湯艷.圖形與幾何[J].貴州教育,2023(Z1):39-46.
[3]王歡.復習課,不妨從學生的認知平衡入手——《立體圖形表面積和體積(復習)》設計與思考[J].教育視界,2022(17):63-65.

