數學建模在初中教學中的實踐

【摘要】數學建模作為數學教育和學習的一個重要組成部分，對于全面提升學生的數學核心素養和推進中學數學素質教育具有深遠影響.本文通過結合具體的教學案例，總結出數學建模在初中數學教學中的具體實踐路徑，主要有構建函數模型，體會數量關系；構建方程組模型，探索問題的本質；構建幾何模型，進行變式訓練；構建概率與統計模型，激發學生思辨能力；構建不等式模型，培養發散思維.

【關鍵詞】初中數學；數學建模；核心素養

數學在生活中無處不在，從簡單的購物計算到復雜的工程設計，都需要數學的支持，數學建模是一個將生活問題轉化為數學問題，再利用數學工具進行求解的過程，這個過程需要抽象思維、邏輯推理和創新能力，對于培養學生的核心素養具有重要意義.這也有助于培養他們的邏輯思維能力、創新能力和實踐能力，培養學生數學核心素養.

1 構建函數模型，體會數量關系

數學建模思想確實是一種強大的工具，能夠將復雜的現實問題轉化為簡化的數學形式，以便于分析和解決.在數學教學中，為了使學生更好地理解數學建模，教師可以選取一些與學生生活密切相關的問題作為建模對象.例如，可以探討如何通過數學建模來優化學校的時間表安排，或者預測某種商品的銷售趨勢等.

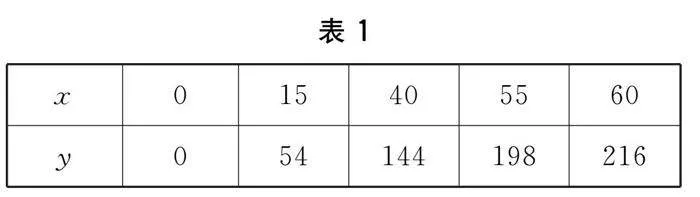
例如 以一次函數的應用為例，這一章節的任務旨在讓學生理解并掌握一次函數的基本概念和性質，學會從實際問題中抽象出一次函數模型，并通過不同的信息來源（如文字描述、數據表格、圖像等）來確定一次函數的表達式.這一章節的學習不僅為學生后續學習更復雜的函數（如反比例函數、二次函數等）打下基礎，而且通過實際問題的解決，培養學生的數學建模能力和問題解決能力.如某體重秤稱重有效范圍是0～100kg，體重x（kg）與指針的轉過角度y的對應值如下表1所示：

請問，如果小華的體重是60kg，他站在體重秤上后，指針會指向哪里？通過這樣的問題，教師可以引導學生分析題目中的信息，幫助他們理解體重和指針位置之間的一次函數關系.通過表格，學生可以直觀地看到數據的變化趨勢，從而更容易理解一次函數的概念和性質；在這個過程中，教師可以鼓勵學生利用描點畫圖的方式來分析函數表達式，這種教學方式不僅能夠激發學生的學習興趣和主動性，還能夠培養他們的自主學習能力和探索精神，通過這個過程，學生能夠實現知識由表象到本質的深化，真正理解和掌握一次函數的應用.

2 構建方程組模型，探索問題的本質

方程模型是數學中一種非常重要的工具，廣泛應用于各種實際問題中，這種轉化過程不僅有助于學生更深入地理解問題的本質，還能夠提高他們的創造性思維能力.為了幫助學生更好地掌握這種能力，數學教師在教學中可以通過設置分層分類的問題，逐步引導學生選擇和運用數學概念、公式和定理等構建數學模型來描述變量之間的關系，這種教學方式不僅有助于提高學生的數學技能，還能夠培養他們的邏輯思維能力和創新能力.

例如 以應用二元一次方程組為例，以增收節支教學為例，教師采取了一個富有創意和實用性的教學策略，即將學生引入實際生活的場景，通過收集和分析家庭水費數據，理解并掌握如何應用二元一次方程組來解決實際問題.在此基礎上，教師進一步引導學生將這種方法應用到更復雜的實際問題中，如公司利潤的計算，通過分析去年的利潤、今年的總產值和總支出的變化率，學生需要列出二元一次方程組來求解去年的總產值和總支出.“某公司去年的利潤（總產值—總支出）為200萬元.今年總產 值比去年增加了20%，總支出比去年減少了10%，今年的利潤為780萬元.去年的總產值、總支出分別是多少萬元？”為了解決這個問題，我們需要使用數學模型.設去年的總產值為 x 萬元，總支出為 y 萬元.根據題目，我們可以建立以下方程：

去年的利潤是x－y=200 萬元（總產值-總支出）；

今年的總產值比去年增加了20%，即今年的總產值為1.2x 萬元；

今年的總支出比去年減少了10%，即今年的總支出為0.9y 萬元；

今年的利潤是1.2x－0.9y=780萬元；由此，我們得出一元二次方程組：

x－y=2001.2x－0.9y=780

通過解決這類實際問題，學生不僅可以掌握方程模型這一有效的數學工具，還可以增強他們的經濟意識和資源意識，這種綜合性的學習實踐過程對于促進學生的全面發展和提高他們的綜合素質具有重要意義.

3 構建幾何模型，進行變式訓練

初中數學教材中蘊含了豐富的模型思想，尤其是在幾何圖形的學習中，幾何圖形，如三角形、四邊形和圓等，不僅是數學的基礎知識，也是培養學生數學建模能力的重要載體.為了幫助學生更好地掌握數學建模的思想和方法，教師可以通過不斷地練習和反思，學生可以逐漸學會培養他們的創新思維和問題解決能力.

例如 初中數學幾何中的勾股定理，李叔叔檢測石獅雕塑底座，如圖1所示：

李叔叔想確定正面的AC邊和BD邊是否都垂直于底邊AB.他只帶了一個卷尺，已測得AC=30厘米，AB=40厘米，BC=50厘米.我們如何幫助李叔叔判斷AC邊是否垂直于AB邊呢？另外，如果小亮只有一個20厘米的刻度尺，他能否用這個工具來檢測AC和BD邊是否垂直于AB邊？

對于李叔叔的情況，我們可以使用勾股定理來驗證，如果AC2+AB2=BC2，那么AC邊就是垂直于AB邊的.我們計算得到：AC2+AB2=2500，BC2=2500，所以AC邊是垂直于AB邊的.

對于小亮的情況，他有一個20厘米的刻度尺，要檢驗AC邊是否垂直于AB邊，他可以嘗試以下方法：

如果AC的長度小于20厘米，他可以直接在AC上測量一個點E，使得AE的長度為10厘米（因為20厘米的一半是10厘米）；

然后，小亮使用刻度尺從A點沿著AB方向測量10厘米到點F；檢查EF是否與AB垂直.如果EF與AB垂直，那么由于AE和AF的長度相等，并且都是10厘米，根據等腰直角三角形的性質，AC也應該與AB垂直.

對于BD邊是否垂直于AB邊，小亮同樣可以使用類似的方法，但這次他需要在BD上測量.

在勾股定理的模型應用中，教師應該注重學生的探索和實踐能力，設計一些與現實生活相關的問題情境，讓學生運用所學的數學知識進行解決，從而提高他們的數學應用能力和問題解決能力.

4 構建概率與統計模型，激發學生思辨能力

統計建模和概率建模是數學在現實生活中的應用，特別是在處理大量數據和隨機現象時，在初中階段，學生開始接觸這些概念，為他們在更高層次上的學習和將來的職業生涯打下基礎.統計建模是一個系統的過程，它包括數據的收集、整理、分析和解釋.這個過程旨在從數據中提取有用的信息，建立數學模型以預測或解釋某些現象.在初中階段，學生通常會學習如何進行抽樣調查，如何計算基本的統計量（如平均數、中位數、眾數、方差等），以及如何繪制圖表（如條形圖、折線圖、餅圖等）來直觀地展示數據.概率建模則關注隨機事件發生的可能性.概率是一種數學工具，用于描述隨機現象的結果.在初中階段，學生將學習基本的概率概念，如事件、隨機事件、獨立事件、互斥事件等，此外，學生還將學習如何使用概率來解決實際問題，如預測比賽結果、評估風險等.

例如 為了估計池塘的螃蟹數量，我們采用了“抓、放、抓”的方法，首先，我們抓上來n只螃蟹，給它們打上標記，然后再放回池塘，之后，我們再次進行捕撈，并觀察每a只螃蟹中有b只是有標記的，目標是利用這些信息來估算池塘中總的螃蟹數量.根據題目，我們可以建立以下模型：

第一次捕撈并標記了n只螃蟹；

第二次捕撈時，每a只螃蟹中有b只是有標記的；

因此，我們可以得出以下結論：

在第二次捕撈的a只螃蟹中，有標記的螃蟹所占的比例應該與池塘中所有有標記的螃蟹所占的比例相近，即：nT≈ba.現在我們要來解這個方程，找出 T 的值，計算結果為：T=anb.

通過這個問題，學生可以體驗到數學在現實生活中的應用，并且學習到如何運用數學知識和邏輯思維來解決實際問題.在解決這個問題時，他們首先需要理解問題的本質，即如何通過有限的樣本信息來估計總體的數量；然后運用統計和概率的知識來建立數學模型.這種從具體到抽象、從簡單到復雜的教學方法有助于學生逐步深化對數學知識的理解，并培養他們的數學建模能力.

5 構建不等式模型，培養發散思維

不等式模型是數學中一種強大的工具，特別適用于解決現實世界中那些涉及不確定數值或需要確定某個量變化范圍的問題，這些問題通常存在于各種實際場景中，如最佳方案選擇、交通運輸規劃、生產規劃以及方案設計等.在這些領域中，不等式模型能夠幫助我們理解和分析問題的本質.這種方法不僅有助于我們更全面地理解問題，還可以為制定決策提供科學依據.

例如 某工廠計劃生產兩種產品A和B，其中A產品的利潤為每件30元，B產品的利潤為每件20元.工廠的總投資為100000元，且用于生產A產品的資金不能超過總投資的60%.同時，工廠每天最多能生產A產品100件和B產品150件.如果工廠想要最大化總利潤，應該如何安排生產？

解決這個問題首先要定義變量，設生產A產品的數量為x件，生產B產品的數量為y件，總利潤為Z，之后構建不等式模型：

利潤最大化，Z=30x+20y（總利潤是A產品和B產品利潤之和）；

資金限制，30x+20y≤60000（A產品和B產品的總成本不能超過總投資的60%）；

生產能力限制，x≤100和y≤150（每天最多能生產A產品100件和B產品150件）.

這個例題展示了如何使用不等式模型來解決一個涉及資源分配和利潤最大化的實際問題，通過構建合適的不等式模型，我們可以找到滿足各種限制條件的最佳解決方案.

6 結語

數學建模是一個多元化且廣泛應用的領域，它可以從不同的角度進行分類，為了更有效地增強學生的數學建模意識，初中數學教師可以從學生日常生活中熟悉的問題入手，并運用數學方法進行求解，幫助學生形成一個數學建模的框架，提升他們的數學核心素養，并為他們未來的學習和職業生涯打下堅實的基礎.

參考文獻：

［1］賓朝路.基于數學學科核心素養的初中數學解題教學研究——以2023年重慶中考數學為例［J］.數理天地（初中版），2024，（03）：35-36.

［2］雷業紅，王小琪.滲透建模思想，強化數學能力——初中數學教學中學生建模素養發展路徑［J］.中學數學，2024，（02）：16-17.