新課改下初中數學跨學科主題教學探究

【摘要】新課標明確提出了跨學科主題學習這一新穎的教學方法，用于開展綜合與實踐活動.在新課改的背景下，跨學科主題教學成為一種有效的教學策略，有助于全面提升學生的核心素養，幫助其健全知識框架，靈活使用知識和技能，還能推動學科教育改革，具有不可忽視的價值.數學作為一門基礎性課程，教師要把握數學和其他學科知識的契合點，豐富教學內容和方法，才能夠進一步發散學生思維，提高學生解決問題的能力.本文就新課改下如何進行初中數學跨學科主題教學展開探討.

【關鍵詞】跨學科教學；初中數學；課堂教學

新課改明確了素養本位的課程取向，教師在教學中應重視跨學科課程的設計，并以發展學生核心素養為目標，增強學生情感體驗，讓學生在跨學科學習中真正體會各個知識點的聯系及應用價值，在積累活動經驗的基礎上，遷移和應用知識及技能，進而充分發揮主觀能動性，發展高階思維，形成跨學科的應用意識與能力.

1 跨學科學習的內涵

不同學者對于跨學科學習的內涵詮釋不同，德國著名數學家Klein J T持有這樣的觀點，他認為跨學科學習是學習者富有創造性地將某一主題的多個學科知識相互關聯起來，進而實現對相關內容的整合過程.而美國學者Lttuca L R則進一步指出，跨學科學習的核心在于將不同領域的知識進行整合，以形成對某一主題更全面、深入的理解，引導學生從不同的角度分析問題，培養學生比較、聯系等解決復雜問題的能力.

可見，不論是哪種觀點都強調了不同學科知識的內容和方法，而跨學科學習并不是單一地將不同學科知識融合起來，也不是單一地運用相關方法解答現實問題，而是體現了綜合性，構建了新的體系或方法來解決現實問題，也是對多種學科知識的運用和鞏固，對新知識的探究，具有獨特的目標和性質.目前，隨著教育改革發展，STEM教育、STEAM教育等都是跨學科學習的類型之一［1］.

2 新課改下初中數學跨學科主題教學的策略

2.1 創設真實情境，培養學生跨學科學習意識

新課標中提出，教師應創設真實情境，幫助學生從中抽象出數學問題，并綜合利用跨學科知識和方法分析推理.在不同的情境中，學生的學習興趣和思維能力是不同的，教師結合教學內容和重難點，依托多媒體技術為學生提供了解生活的機會，并在生活中抽象出實際問題，不僅能開闊學生視野，還能促使其從不同的角度分析問題、思考和表達.同時，教師可以將其他學科知識融入其中，注重引導，充分挖掘各類問題并指導學生運用多門學科知識解決問題.幫助學生從不同的角度去思考，逐步發展其思維能力，培養學生運用跨學科知識解決問題的意識和技能［3］.

例如 在教學反比例函數時，教師可以將其和物理知識結合起來，為學生創設杠桿撬物體的情境.教師可以利用多媒體展示一個杠桿撬物體的動畫或實物演示，讓學生了解杠桿的基本原理和應用.然后，教師提出問題：“假設我們有一個固定的支點O，一個不變的阻力和阻力臂，我們如何調整動力（F1）和動力臂（L1）來更省力地撬動物體呢？”教師將全班學生劃分為若干小組，每組提供一套杠桿實驗器材，包括不同長度的杠桿、砝碼等.教師指導學生進行實驗操作，記錄不同動力臂和動力下的實驗結果.學生根據實驗數據，繪制出動力和動力臂之間的關系圖，并觀察圖形特點.通過數據分析，學生發現當阻力和阻力臂不變時，動力和動力臂的乘積是一個定值，即動力（F1）×動力臂（L1）=阻力（F2）×阻力臂（L2）或F1F2=L2L1.教師引導學生將實驗結果轉化為數學模型，即反比例函數關系.教師解釋反比例函數的定義和性質，并引導學生理解在這個特定情境中，動力和動力臂是如何構成反比例關系的.學生分享自己的實驗過程和發現，討論動力和動力臂之間的關系以及這種關系在實際生活中的應用.教師可以引導學生思考其他類似杠桿的情境，如滑輪、輪軸等，并探討它們是否也遵循類似的數學規律.在此基礎上，教師還可以進一步拓展這一案例，將反比例函數與其他學科知識相結合.例如，可以引入物理學中的電學知識，解釋電阻、電流和電壓之間的反比例關系；或者引入化學中的濃度問題，解釋溶質質量與溶液體積之間的反比例關系.如此，物理知識在數學知識中呈現，幫助學生借助熟悉的物理知識理解反比例函數，進一步認識各個函數的數量關系，滲透科學精神.

2.2 設計驅動問題，培養跨學科學習能力

初中學生已經具備了一定的思維能力，為了促進學生核心素養發展，進一步提高其邏輯思維、創造思維，教師應積極發揮問題的價值，并結合實際情況，設計多樣化的驅動問題，以此激發學生的探索欲，啟發學生從多角度分析，掌握跨學科學習的相關策略.通過跨學科問題的設計，促進學生思維的深度蔓延，進而達到預期的教學目標，提高學生質疑能力、推理能力等.

例如 教師可以首先通過一則小故事或生活中的實例來激發學生的興趣.例如，講述一個小朋友在喝糖水時不斷加糖，發現糖水變得越來越甜的過程，然后提出問題：“為什么加糖后糖水會更甜呢？這背后隱藏著什么數學原理呢？”要求學生用數學知識解釋這一現象.學生結合自己的理解，從數學的角度進行分析，將生活問題轉換為抽象的數學問題，并用數學語言解釋其中的數量關系，進一步感知數學的魅力.教師可以指導學生設計一個簡單的實驗，準備不同濃度的糖水樣本，并邀請學生品嘗，記錄各自的感受.學生根據品嘗結果，記錄不同濃度下糖水的甜度感受，并嘗試用數學語言描述這種感受.如可以設定一個甜度評分系統，用數字表示不同濃度下的甜度.基于實驗數據，學生建立數學模型，將糖水的甜度認為是糖水中糖a和糖水b的質量比ab，且b＞a＞0，在糖水中加糖m，變為a+mb+m，且a+mb+m＞ab.那么，如何證明a+mb+m＞ab呢？學生運用數學方法進行推理分析：因為ab-a+mb+m=ma－bbb+m，a＜b，顯然a-b＜0，所以ma－bbb+m＜0，則a+mb+m＞ab，證實了糖水繼續加糖之后，糖和糖水的質量之比變大了，現象就是糖水變甜了.學生用數學語言解釋生活中的現象，對于糖水加糖就更甜這一情況，可以用：b＞a＞0，當m＞0時，ab＜a+mb+m.同時，學生可以直觀推理出ab＜a+mb+m.如此，學生透過現象看本質，應用跨學科知識將感性的問題變得抽象，再變得具體，在問題的驅動下，學生積極思考，應用推理等能力解決問題，也更好地理解現實生活中的數學模型.

2.3 豐富學習方式，掌握跨學科學習方法

跨學科主題學習的特點就是多樣化，在這樣的背景下，學生的學習方法和思維是不受局限的，不管是哪種學習方式，教師都應予以學生充足的時間和空間，引導其自主探究.在教學中，教師應有意識地豐富教學方法，如小組合作、情境創設、角色扮演等，并通過綜合性的問題，引導學生觀察分析、猜測聯想、推理論證、交流反思，只有充分激發學生的學習興趣，才能逐步發展其探究精神，并在學習的過程中形成獨立思考能力、團隊協作能力等［4］.

例如 教師可以創設教學主題“體育運動與心率——探究函數關系與實際應用”，教師首先通過一段視頻展示不同體育運動中人們的心率變化情況，以此激發學生的好奇心和探究欲望，教師提出問題：“體育運動與心率之間有著怎樣的關系？我們能否用數學來描述這種關系？”而后，教師將學生按照興趣和能力分組，每組選定一種體育運動（如跑步、跳繩、游泳等）作為研究對象.教師為每個小組分配數據收集工具（如心率監測器、計時器等），并講解數據收集的方法和注意事項.學生在教師的指導下進行運動實驗，記錄不同運動強度下的心率數據.實驗過程中，學生需要注意控制變量，確保數據的準確性和可靠性.學生將收集到的數據進行整理、分類和統計，繪制出心率隨運動強度變化的散點圖.在此基礎上，學生觀察散點圖的趨勢，嘗試用函數模型來描述心率與運動強度之間的關系.教師引導學生思考可能的函數類型（如線性函數、二次函數等），并幫助他們理解如何選擇合適的函數模型.學生利用新的實驗數據來驗證所建立的函數Y1rkxqMp2jL+YwaO4H5M8g==模型是否準確，如果模型與實際數據存在較大偏差，其需要重新審視模型的選擇和建立過程，進行必要的調整和優化.最后，學生將他們的研究成果以報告、PPT或海報的形式進行展示，分享他們在探究過程中的發現、體會和收獲.其他小組可以提問或發表意見，形成互動交流的氛圍.

2.4 注重以評促學，強化跨學科學習動力

“教學評”一體化背景下，教師不僅要關注課堂教學內容，還要關注教學評價，通過健全的評價體系，針對學生的個性化特點，通過科學的評價結果幫助學生客觀地認識自己，了解自己的優勢和不足，并輔助學生制訂學習計劃，發展自身學習水平.教師應以核心素養為目標，將評價貫穿學習全過程，包含了過程性評價和結果性評價.同時，評價的維度適當拓展，涵蓋了學生的學習態度、價值觀念、思維能力等.采取紙筆測試、實踐探索等相結合的評價方式，培養學生的跨學科學習能力，進而讓學生主動探究更多的數學問題，達到知識遷移、舉一反三的目的［5］.

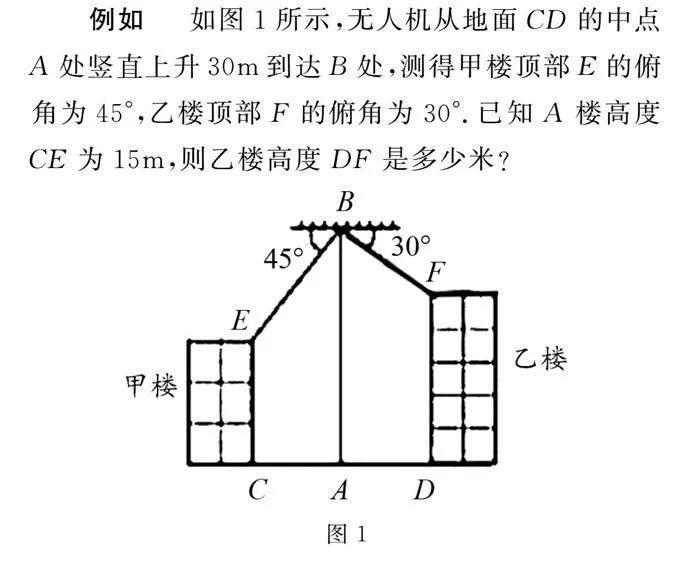
例如 如圖1所示，無人機從地面CD的中點A處豎直上升30m到達B處，測得甲樓頂部E的俯角為45°，乙樓頂部F的俯角為30°.已知A樓高度CE為15m，則乙樓高度DF是多少米？

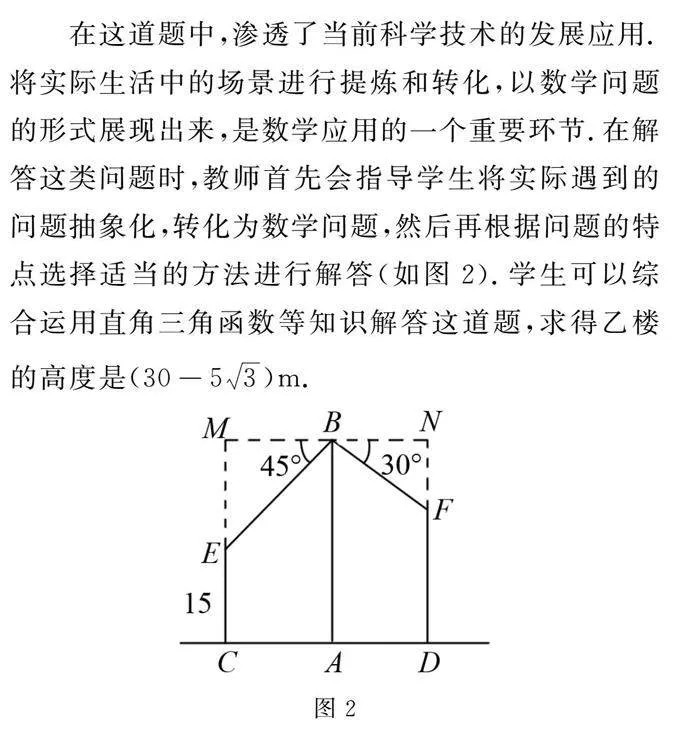
在這道題中，滲透了當前科學技術的發展應用.將實際生活中的場景進行提煉和轉化，以數學問題的形式展現出來，是數學應用的一個重要環節.在解答這類問題時，教師首先會指導學生將實際遇到的問題抽象化，轉化為數學問題，然后再根據問題的特點選擇適當的方法進行解答（如圖2）.學生可以綜合運用直角三角函數等知識解答這道題，求得乙樓的高度是（30－53）m.

3 結語

新課改背景下，跨學科主題教學是必然發展趨勢.教師應正確解讀相關政策和教學大綱，并結合具體的教學內容，整合課內外資源，靈活將其他學科知識融入其中，以發展學生核心素養為導向，突出課堂教學的綜合性，進而促進學生思維深度發展，幫助其掌握更多的知識和學習策略.

參考文獻：

［1］董曉怡.小議初中數學的跨學科項目式教學［J］.河南教育（基教版），2024（02）：83.

［2］林祥榮.基于跨學科綜合視角下的初中數學核心素養的培養與評估［J］.數理化解題研究，2024（02）：17-19.

［3］程曉亮，左瀚文，林殿吉.初中數學跨學科主題學習的設計與實施［J］.教學與管理，2024（04）：39-42.

［4］黃偉群.基于核心素養的初中數學跨學科主題學習［J］.數理天地（初中版），2023（23）：75-77.

［5］陳婷.例談初中數學跨學科教學策略［J］.理科愛好者，2023（05）：83-85.