Polypad工具在數學教學中的應用


摘要:本文介紹了一款實用工具——Polypad,并通過教學片段分析和總結了該工具在數學教學中的應用,希望通過合理運用能夠提高學生學習數學的主動性。
關鍵詞:實用工具;Polypad;教學片段
中圖分類號:G434 文獻標識碼:A 論文編號:1674-2117(2024)19-0093-03
教學片段一:利用Polypad進行平面鑲嵌活動
《義務教育數學課程標準(2022年版)》提出:“初中階段綜合與實踐領域,可采用項目式學習的方式,以問題解決為導向,整合數學與其他學科的知識和思想方法,讓學生從數學的角度觀察與分析問題、思考與表達、解決與闡釋社會生活以及科學技術中遇到的現實問題,感受數學與科學、技術、經濟、金融、地理、藝術等學科領域的融合,積累數學活動經驗,體會數學的科學價值,提高發現與提出問題、分析與解決問題的能力,發展應用意識、創新意識和實踐能力。”“實踐性”是綜合與實踐內容的基本特征之一,而單靠實踐比較耗時、費力,此時若適當借助數字資源輔助教學,則會收到意想不到的效果。下面,筆者以七巧板為例介紹如何設計瓷磚進行平面鑲嵌。具體操作步驟如下:
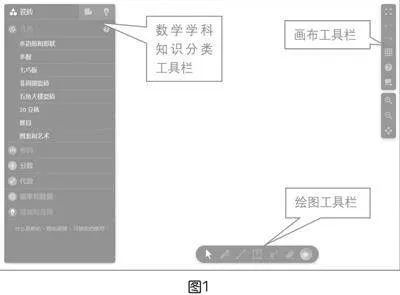
(1)進入Polypad操作界面(如圖1),界面共分三個工具欄,左側工具欄中有幾何、代數和概率等大量實用工具,界面的空白處是畫布區域。
(2)在Polypad界面左側工具欄中打開“幾何”下的“多邊形和形狀”,這里提供了一些常用的多邊形,把一個正方形拖入到畫布中,選中正方形后在圖形下方會彈出一個工具框,選擇“切”工具,把正方形切成兩半。
(3)按照相同的方法,把正方形切成七部分,然后分別設置成不同的顏色進行區別,最后把它們分散排列開來,這樣就制作好了一個七巧板,如下頁圖2所示。學生利用自己制作的七巧板就可以進行鑲嵌活動了。
教學片段二:利用Polypad探尋楊輝三角規律
在數學學習中,學生經常需要通過觀察來探究規律。“楊輝三角”是人教版八年級上冊“閱讀與思考”欄目的內容,利用傳統的教學方式,教師往往難以激發學生參與探究的積極性,因此可以借助Polypad畫布,引導學生繪制龐大的“楊輝三角”,然后從不同角度觀察、探究其中蘊涵的規律。具體操作步驟如下:
(1)在Polypad界面左側工具欄中打開“號碼”下的“號碼卡”,把號碼拖到畫布中并排列成楊輝三角圖形。需要注意的是,利用號碼卡最后一欄中的輸入框可以輸入任意一個號碼,如圖3所示。
(2)引導學生探究楊輝三角中蘊涵的規律。先讓學生全選一行數字,然后選擇復制,接著選擇合并(如圖4),此時所復制的這一行數會自動合成一個數,如第4行的5個數會合成16,重復這樣的操作,學生容易發現每一行各數之和剛好是行數的平方。接著,引導學生繼續合作探究楊輝三角中蘊涵的其他規律。
(3)教師打開“數學游樂場”課程部分的課例資源——帕斯卡三角(楊輝三角),與學生共同欣賞楊輝三角的美,探索、總結楊輝三角中蘊涵的規律。這里的楊輝三角非常龐大、簡潔,而且具有互動性。例如,可以通過不同的顏色,體現從不同角度看到不同的序列以及由這些序列形成的神奇的圖案,如斐波那契數列等。
教學片段三:利用Polypad探究函數圖像的規律
在初中階段,學生主要學習的函數是一次函數、二次函數和反比例函數。以二次函數為例,學生用描點法畫圖,基本上能看出二次函數表達式中的系數與圖像和對稱軸的關系,但是若每次改變a、b、c的值都用描點法畫圖,是比較耗時、費力的,此時可引導學生在Polypad中繪制二次函數圖像并通過改變a、b、c的值來探究圖像的變化規律。具體操作步驟如下:
(1)在Polypad界面左側工具欄中打開“代數”下的“坐標和表格”,把一個坐標軸拖到畫布中,接著打開“代數”下的“可變滑塊”,拖動“a、b、c”三個可變滑塊到畫布中。
(2)選中界面最下方繪圖工具欄中的“x2”方程工具,在畫布中輸入方程“a·x2+b·x+c”,然后單擊它,界面下方出現繪圖圖標(如下頁圖5),單擊它,系統就會自動繪制出二次函數的圖像,改變三個可變滑塊,改變系數的值,函數圖像也會隨著改變。
教學片段四:利用Polypad探究完全平方公式
教科書中的幾何圖形是靜止的,難以激發學生探究的熱情,若讓學生借助Polypad畫布制作“代數瓷片”,構造幾何圖形,則可以大大提高學生參與課堂的積極性。
例如,學生在學習完全平方公式時往往會出現“(x+y)2=x2+y2”的錯誤,若能借助Polypad,通過對面積的討論,學生便可以發現完全平方公式與面積之間的內在聯系,從而更容易記住公式“(x+y)2=x2+2xy+y2”,進而感受到幾何與代數內在的統一性。具體操作如下:
(1)在Polypad界面左側工具欄中打開“代數”下的“代數瓷片”,依次將面積為x2、y2、xy的矩形拖到畫布中,拼接成如圖6所示圖形。
(2)當Polypad界面左側工具欄中沒有現成的“代數瓷片”時,可以教學生自己制作瓷片,如要在Polypad畫布中構造圖形說明等式“(x+3)2=x2+6x+9”,可以操作如下:
①從Polypad界面左側工具欄中拖動面積為x2的瓷片,然后點擊畫布下方工具欄中的“復制”按鈕,復制三份備用。
②單擊第1張備份瓷片,點擊畫布下方工具欄中的“水平分割”按鈕,點擊2次,便可將其平均分成4份,然后點擊畫布下方工具欄中的顏色按鈕,將顏色設置為綠色,并在這些瓷片上標注“x”,拖動其中的3份,拼接到瓷片(x2)下方。類似地,單擊第2張備份瓷片,點擊畫布下方工具欄中的“垂直分割”按鈕,點擊2次,便可將其平均分成4份,然后點擊畫布下方工具欄中的顏色按鈕,將顏色設置為綠色,并在這些瓷片上標注“x”,拖動其中的3份,拼接到瓷片(x2)右方。
③單擊第3張備份瓷片,先后點擊畫布下方工具欄中的“水平分割”和“垂直分割”按鈕各2次,便可把這塊瓷片平均分成16份,然后點擊畫布下方工具欄中的顏色按鈕,將顏色設置為橙色,在這些瓷片上標注“1”,然后拖動其中的9份依次拼接到剛才所得圖形的右下方,得到一個正方形,這個正方形可以直觀表達等式“(x+3)2=x2+6x+9”。
(3)滑動Polypad界面左側工具欄下方的“x滑條”,可調整畫布中圖形的大小。學生可以用類似的方法,在畫布中構造不同的圖形來表示不同的等式,如x2-4x+4=(x-2)2,x2+6x+2=(x+3)2-7等,學生在操作中得以從幾何的角度直觀地理解完全平方公式和“配方”,體會幾何與代數內在的統一性,感悟數形結合思想。
限于篇幅,Polypad更多的應用有待大家自行探索。
基金項目:廣西教育科學“十四五”規劃2023年度課題“初中數學項目式學習的實踐與研究”(編號:2023C402)。

