數形結合思想在高中生物解題中的運用

摘要：本文旨在探討數形結合思想在高中生物解題中的運用.通過對高中生物教材的深入解析，結合數學和幾何概念，提出了一種新的解題方法.以實例分析為主要研究手段，通過對生物學知識和數學原理的巧妙融合，展示了這一方法的高效性和實用性.

關鍵詞：數形結合；高中生物；解題方法；人教版教材；實例分析

中圖分類號：G632文獻標識碼：A文章編號：1008-0333（2024）27-0131-03

在解題過程中，許多學生往往容易陷入死記硬背的困境，難以理解和應用其中的數理思想.本文旨在通過數形結合思想，為高中生物解題提供一種全新的思路.數學和幾何的概念可以被靈活地運用于生物學中，通過對生物現象的量化和幾何化，我們可以得到更直觀、精確的解題結果.

1數形結合思想的理論基礎

數學和生物學緊密相連，廣泛應用于多個領域：概率論用于遺傳學研究，預測基因型和表現型頻率；微積分在生態學中描述生物群體變化和相互作用；統計學支持流行病學研究，分析疾病傳播風險［1］.數學為生物學提供量化、建模和預測工具，促進跨學科研究，深化生命科學的理解.

2數形結合在高中生物解題中的具體運用

2.1實例一：生態系統的穩定性與數學模型

2.1.1生態平衡的數學描述

生態平衡指在一個生態系統中，各種生物種群之間的相互作用保持相對穩定的狀態，使得生態系統內的物質和能量的循環達到一種相對穩定的狀態［2］.在數形結合的思想下，我們可以利用數學模型來描述生態平衡.一個典型的例子是捕食者-被捕食者模型，也稱為Lotka-Volterra模型.這個模型描述了捕食者（如狐貍）和被捕食者（如兔子）之間的相互作用.

模型的基本假設包括：兔子的繁殖率與食物充足程度成正比、狐貍的繁殖率與捕食的兔子數量成正比、兔子的死亡率與被狐貍捕食的可能性成正比、狐貍的死亡率與食物稀缺程度成正比.數學模型的基本方程如下：

對于兔子種群：dR/dt=rR-aRF

對于狐貍種群：dF/dt=-sF+bRF

其中，R表示兔子的種群數量；F表示狐貍的種群數量；r是兔子的繁殖率；a是捕食者對兔子的捕食率；s是狐貍的死亡率；b是狐貍每捕食一只兔子獲得的繁殖機會.

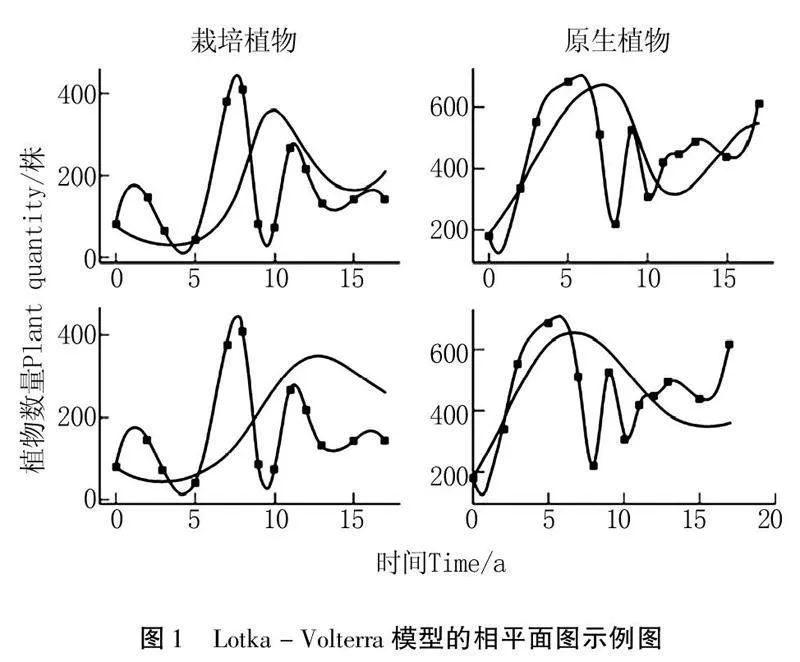
這個模型通過一系列微分方程描述了兔子和狐貍種群隨時間的變化.通過求解這些方程，可以獲得在不同初始條件和參數設定下，種群數量隨時間的變化情況.當初始條件為R=100 和 F=20，參數設定為 r=0.1， a=0.01， s=0.1， b=0.005 時，可以通過求解模型方程得到兔子和狐貍種群隨時間的變化曲線（如圖1），從而了解它們之間的相互作用和穩定狀態.

2.1.2穩定性分析的幾何解釋

在研究捕食者-被捕食者模型時，相平面成為一種重要的分析工具.相平面將生態系統的種群數量用二維坐標系表示，橫軸代表被捕食者（如兔子）的種群數量 R，縱軸代表捕食者（如狐貍）的種群數量 F.通過在相平面中繪制模型的微分方程向量場，可以清晰地觀察到每個點 （R，F） 處的種群數量變化趨勢.

穩定點是在模型中，種群數量不再發生變化的特殊點.換句話說，在穩定點上，種群數量的變化率為零，可以通過繪制零等值線來描繪出這些穩定點的位置.零等值線是在模型中，種群數量變化率為零的曲線或曲面，通過相平面可以直觀地展示出這些線條.

穩定性分析是判斷穩定點特性的關鍵步驟，可以通過觀察向量場和零等值線的交叉情況，來判斷穩定點的穩定性.當一個穩定點周圍的箭頭方向都指向該點時，該穩定點就是一個穩定的平衡點，這表示在該點附近的種群數量不會出現明顯的波動.

相軌道是描述種群數量隨時間變化的曲線，它們展示了種群數量之間的相互作用和變化趨勢.通過相軌道，可以更清晰地了解捕食者-被捕食者模型中的種群數量的動態演變.這種幾何解釋提供了一種直觀、直接理解生態系統穩定性的方法，也為設計保護措施提供了重要參考.通過相平面的分析，能夠更有效地理解生態系統中捕食者和被捕食者之間的相互作用，為保護生態平衡提供科學依據.

2.2實例二：遺傳與概率統計的結合

2.2.1遺傳規律的數學表達

在遺傳學中，孟德爾的遺傳定律是至關重要的基石之一.這些定律包括了隱性性狀的表達，而通過數形結合，能夠借助概率統計來量化描述這些遺傳規律[3].孟德爾提出了兩條關鍵定律，分別是隱性性狀的分離定律和獨立性狀的自由組合定律.

隱性性狀的分離定律描述了在雜合子與純合子交叉的情況下，后代的表型現象.這意味著后代會攜帶兩種不同的基因，但只會表現出其中一個基因的性狀.通過概率統計，我們能夠精確地計算出各種表型的比例.舉例來說，如果一個雜合子父本（Aa）與一個純合子母本（aa）交叉，后代表型為“a”的概率將會達到50%.

獨立性狀的自由組合定律描述了在多個基因對相互獨立時，它們的組合也是相互獨立的.這意味著可以通過概率的乘法規則來計算后代的基因型組合.考慮兩對基因（AaBb）的交叉，能夠通過概率計算獲得各種基因型的后代比例.

數學表達和概率統計能準確描述遺傳過程中基因型的概率分布，幫助學生精確理解和預測后代遺傳特征.這種數形結合方法深化了對遺傳學規律的理解，展示了其在生物學中的重要應用.學生能以更科學的方式探索遺傳學，為未來研究和實踐奠定基礎.

2.2.2遺傳特征的概率分布模型

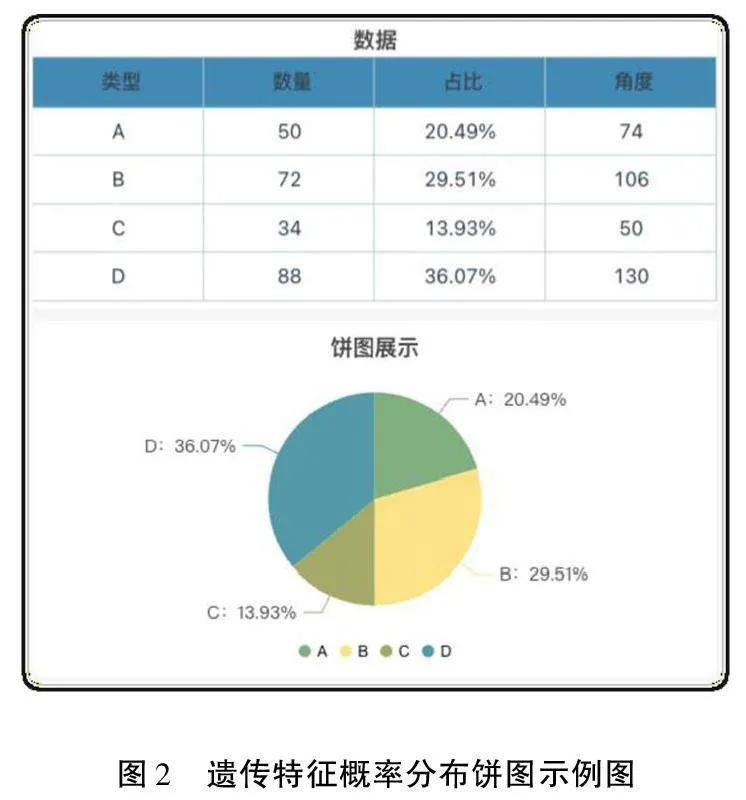
當涉及孟德爾的遺傳定律以及隱性性狀的分離定律時，可以借助概率分布模型（如圖2）來更具體地描述遺傳特征.隱性性狀的分離定律涉及兩個個體，一個是雜合子（Aa），另一個是純合子（aa）.大寫字母代表顯性基因，小寫字母代表隱性基因.

在隱性性狀的分離定律中，考慮到父本基因型為Aa，母本基因型為aa的情況.根據概率規則，可以列出可能的子代基因型，分別為Aa（隱性性狀表現）和 aa（隱性性狀表現）.因此，子代的基因型分布模型為Aa：50%，aa：50%.此外，表型分布模型也應考慮到隱性性狀只在兩個基因都是小寫字母（aa）的情況下才會表現出來，故子代的表型分布模型為顯示表型（Aa）：50%，隱性表型（aa）：50%.

接下來探討獨立性狀的自由組合定律，假設有兩對基因（AaBb）的交叉.根據概率規則，可以列出可能的子代基因型，包括AABB、AABb、AaBB、AaBb、aaBB、aaBb、Aabb、aabb.因此，子代的基因型分布模型為AABB：25%，AABb：25%，AaBB：25%，AaBb：25%，aaBB：0%，aaBb：0%，Aabb：0%，aabb：0%.

最后，綜合考慮這些基因型的表現情況，假設這兩對基因的表型完全獨立.根據上述基因型分布模型，將其擴展到表型分布模型中，得到了顯示表型（AaBb）：50%，隱性表型（aaBB、aaBb、Aabb、aabb）：50%.

通過概率分布模型，能夠量化地描述孟德爾遺傳定律，以及隱性性狀的分離定律和獨立性狀的自由組合定律.這能夠準確地預測后代的遺傳特征，并且為遺傳學研究提供了有力的工具.

3數形結合思想的實際應用效果

3.1實例分析的解題效率比較

以生態系統穩定性為例，傳統方法主要依賴定性描述和自然語言敘述，可能涉及復雜的定性關系和數學符號的直觀解釋.數形結合思想則將生態系統建模為微分方程，通過求解獲得種群數量的具體變化趨勢，并可在相平面上繪制軌跡圖［4］.這種方法能更準確描述生態系統因素間的關系，進行定量分析，預測未來趨勢，并通過可視化方式深入理解生態系統穩定性，相比傳統方法更具直觀性和深度.

3.2學生學習成績的提升情況

數形結合思想的應用顯著提升了學生學習成績，學生需要將生物學概念與數學方法結合，促進深入理解問題.例如，在生態系統穩定性和遺傳學問題中，學生通過建立數學模型和使用概率統計，提高了解題準確度.這種方法要求學生進行定量研究和分析，提升了他們的定量分析能力.同時，圖形和圖表的使用增強了生物學問題的直觀性和可視化效果，如相平面圖能直觀展示種群變化趨勢，幫助學生更好地理解復雜生態系統［5］.4結束語

本文對數形結合思想在高中生物解題中的應用進行了深入研究，并以實例分析為主要研究手段，證明了這一方法在提升解題效率和學生學習成績方面的顯著效果.數學與生物學的結合為高中生物解題提供了新的思路和方法，對于提升教學質量具有積極的推動作用.同時，也為教育教學實踐提供了有益的參考依據.

參考文獻：

［1］ 劉琛.生物學習題中的數形結合思維運用兩例[J].生物學教學，2011，36（02）：59-60.

［2］ 王邦齊.淺談高中生物遺傳題的解題方法[J].科技風，2018（32）：24.

［3］ 曹毅.高中生物解題的幾點思考[J].科學大眾（科學教育），2018（05）：25，134.

［4］ 陳新瑋.高中生物選擇題的解題方法與技巧探討[J].科學大眾（科學教育），2018（03）：22.

［5］ 胡靜宜.高中生物解題技巧的總結與分享[J].科學大眾（科學教育），2018（02）：36.

［責任編輯：季春陽］