干擾觀測器與模糊伺服復合控制策略研究

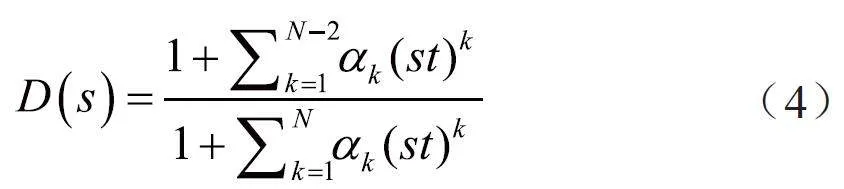
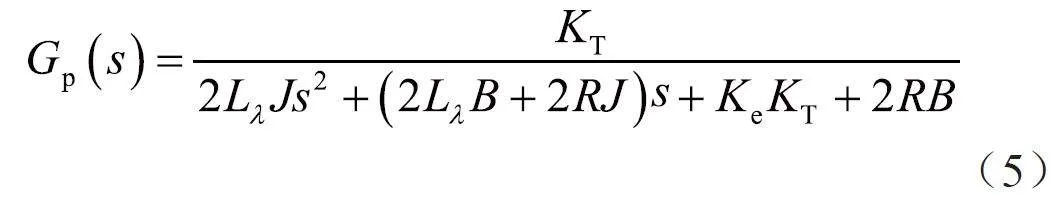
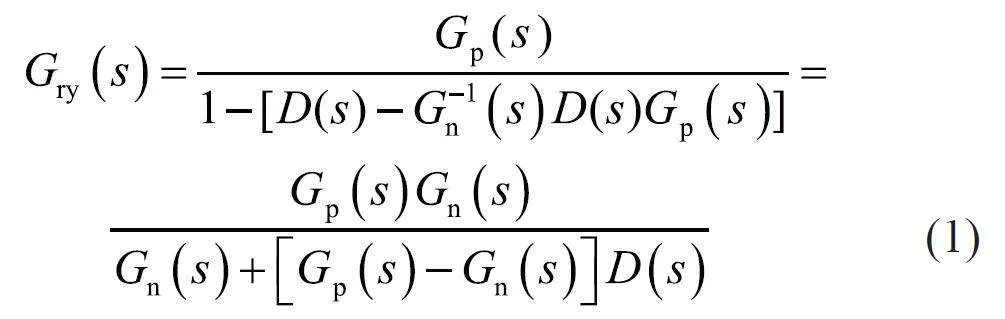
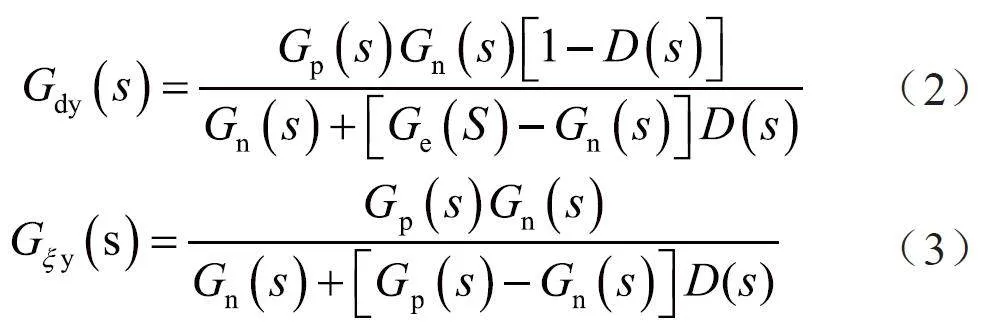
［摘 要］在現代工業伺服控制技術發展中，伺服控制系統的高控制精度、高穩定性和快速響應性是經典控制理論和現代控制原理追求的主要目標，特別是在外界對系統的擾動或難以建立精確的被控對象數學模型的情況下，傳統的單純PID 控制環路抗擾動能力差。文章設計了模糊控制器和干擾觀測器，該控制器能夠補償模型參數不準確所引起的誤差，同時能夠抵抗外界對系統的擾動。

［關鍵詞］PID 控制；干擾觀測器；模糊控制；復合控制

［中圖分類號］TM351 ［文獻標志碼］A ［文章編號］2095–6487（2024）04–0144–03

1 背景

在經典控制方法中，系統輸出的穩定性和控制精度是主要追求目標，PID 控制因其簡易理論基礎，控制過程易于調節且控制效果突出，通過適當改變其控制環路結構，能夠有效改善其輸出效果，因此廣泛應用于工業各控制領域。在實際工業應用中，因控制環境的多樣性，且PID 控制自身的局限性，特別是對于控制對象的不確定性和一些非線性系統，單純PID伺服控制環路已不能滿足控制要求。模糊控制不僅不受限于被控對象精確的模型理論，還能夠適應于一些控制域復雜的非線性系統，因此能夠很好地填補PID控制的一些缺陷。

2 干擾觀測器設計

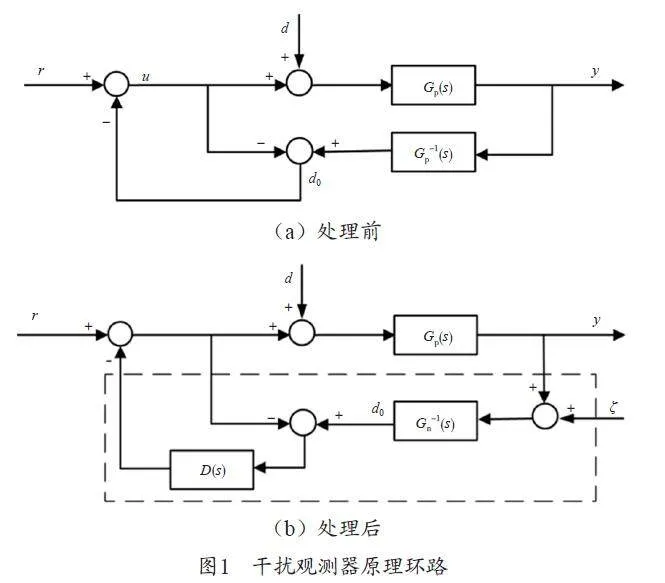
干擾觀測器控制的基本思想是將外部各種干擾因素及模型參數變化引起的實際對象與名義模型輸出的差異等效到控制輸入端，即觀測出等效干擾，在控制系統中引入相等的補償量實現對干擾的完全抑制。干擾觀測器原理環路如圖1 所示。

由圖1（a）可知，等效干擾估計值為：do=（u+d）Gp（s）Gp-1（s）–u=d，其中u 為輸入信號減去反饋信號，d 為外界干擾，Gp（s）為被控對象傳遞函數，do 為干擾估算值，由此可看出，外界對系統的干擾是可以估算的。

在實際控制系統中，被控對象的傳遞函數為正則，分析圖1 可發現，在環路圖中引入了被控對象傳遞函數的逆函數，可通過在圖1（a）中引入一個低通濾波器來滿足，同時考慮引入測量噪聲的影響，經過處理后的原理如圖1（b）所示，圖中虛線框內為干擾觀測器，其中ξ、Gn-1（s）和D（s）分別為測量噪聲、名義模型的逆和低通濾波器。

利用梅遜公式可求得圖1 中輸入信號r、干擾d、測量噪聲ξ 對系統輸出y 的傳遞函數：

式中，N與系統階次成正比，k為傳遞函數階次，t為時間。

同理：

對D（s）的設計準則通常采用的是在低頻段D（s）=1 和在高頻段D（s）=0，由此對上述公式進行分析可得：在低頻段Gry（s）=Gn（s），Gdy（s）=0 和Gξy（s）=1，在高頻段Gry（s）=Gp（s），Gdy（s）=Gp（s）及Gξy（s）=0。由此分析可知，在低頻段時實際被控對象對系統輸入時響應的傳遞函數與名義模型一致，Gdy（s）=0 說明低通濾波器能夠完全抑制低頻干擾，Gξy（s）=1 說明在低頻段測量噪聲ξ 對干擾觀測器的影響非常大。

對于低通濾波器的設計可采用以下公式：

3 模糊控制器構建

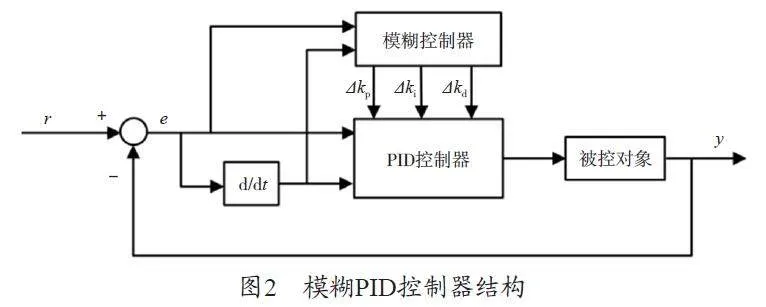
模糊PID 復合控制策略：模糊控制能夠適應非線性特性控制對象，且魯棒性好，控制精度主要由模糊規則庫決定，由于沒有積分（I）的作用，在實際的伺服控制應用中不能消除靜態誤差，而模糊PID 復合控制能夠充分發揮各自控制優勢。模糊PID 控制器結構如圖2 所示。

若x 的物理論域為[X，–X]，模糊論域為[F，–F]，則量化因子kf=F/X，同時需要保證經過量化因子處理后的變量值在模糊論域范圍內，若被控對象需要輸入的物理論域為[P，–P]，則比例因子kx=P/X。模糊規則庫可利用MATLAB/Simulink 工具建立，如在實際控制應用中，當|e| 較大時，為了能夠增加系統響應速度，同時為了提高系統動態穩定性，kp 應取較大值，且kd 應取較小值，同理對于變量e 或ec，其他輸入情況同樣能夠建立這種輸入變量與輸出變量間的對應關系。

4 觀測器PID控制試驗

假設被控對象為1 個伺服電機，其傳遞函數為線電壓U 與轉子角速度w（t）輸入輸出的關系w（s）/U（s），即無刷直流電機傳遞函數Gp（s）為：

式中，Ke為反電動勢系數，R為定子繞組的電阻值，J為電機轉子轉動慣量，B為粘性阻尼系數，KT為轉矩常數，L為三相定子繞組自感，M為定子繞組間互感（L–M=Lλ）。

令K1=2LλJ，K2=2LλB+2RJ，K3=KeKT+2RB，可得：

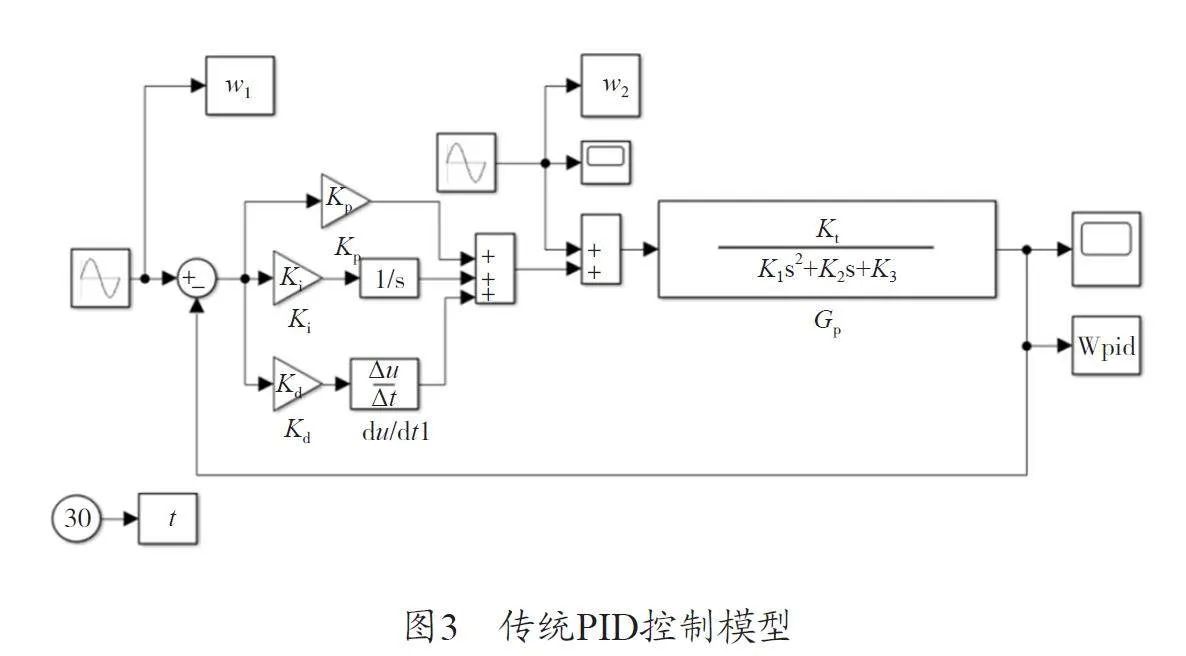
通過MATLAB/Simulink 建立的傳統PID 控制模型如圖3 所示。

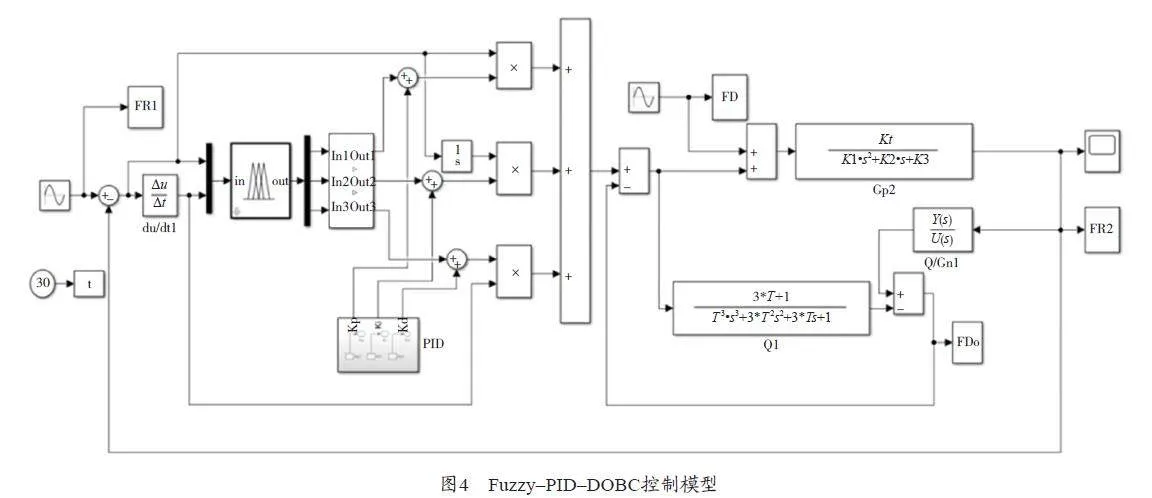
建立基于觀測器控制的模糊PID 控制（Fuzzy–PID–DOBC）模型，如圖4 所示，系統輸入信號及信號變化率輸入到模糊控制器，模糊控制器輸出作為PID控制環路的輸入，與PID 控制綜合實現控制參數的在線整定，能夠減少系統調節時間，還能夠提高系統的魯棒性。DOBC 處于內環，其輸入為模糊PID 復合控制的輸出。根據Fuzzy–PID–DOBC 控制輸出結果，其誤差范圍在–0.013～0.012。

5 結束語

文章根據模糊控制基本思想構建了模糊控制器，在完成干擾觀測器設計和模糊控制器構建的基礎上，利用MATLB/Simulink 建立了基于干擾觀測器控制的模糊PID 復合控制策略模型并完成了試驗。研究結果表明，引入干擾觀測器之后對系統擾動有明顯的抑制作用，控制精度明顯提高。同時為了系統能夠實現控制參數在線整定、提高系統響應速度和增加系統魯棒性，引入了模糊控制，根據輸出結果可知，顯著改善了系統性能。

參考文獻

[1] 劉金琨. 先進PID 控制MATLAB 仿真：第3 版[M]. 北京：電子工業出版社，2011.

[2] 劉經偉，周瑞，朱敏玲. 先進模糊智能復合經典PID 控制理論與應用及其MATLAB 實現[M]. 北京：首都經濟貿易大學出版社，2016.

[3] 李國勇，楊麗娟. 神經· 模糊· 預測控制及其MATLAB實現：第3 版[M]. 北京：電子工業出版社，2013.