基于支持向量回歸的數控加工刀軌自動規劃方法

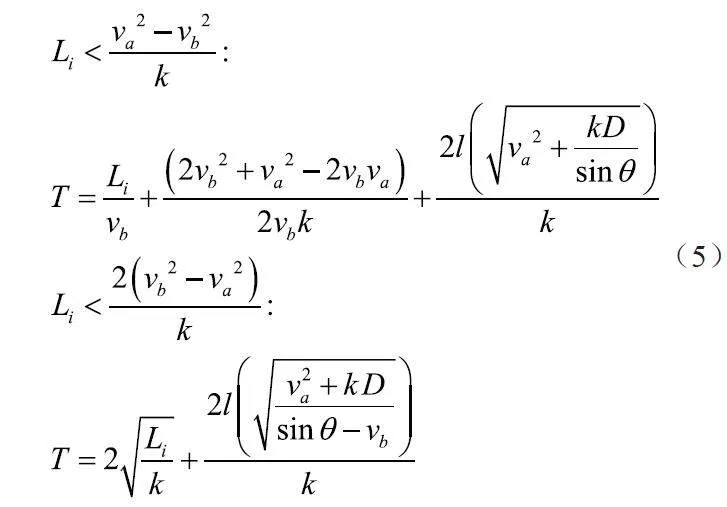
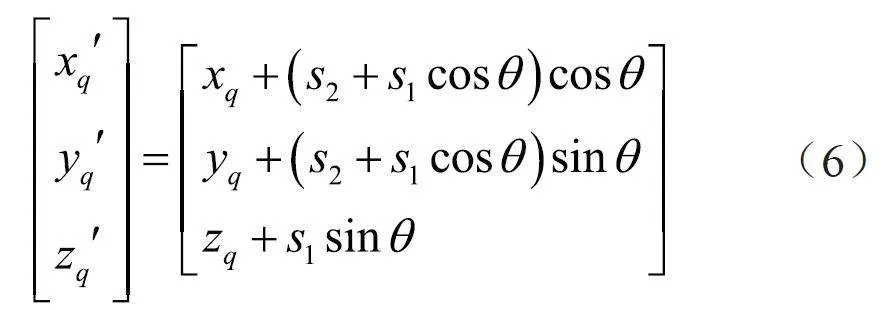
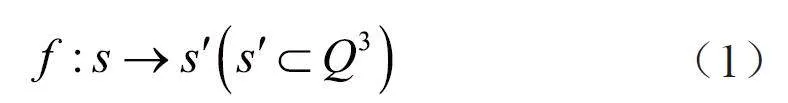

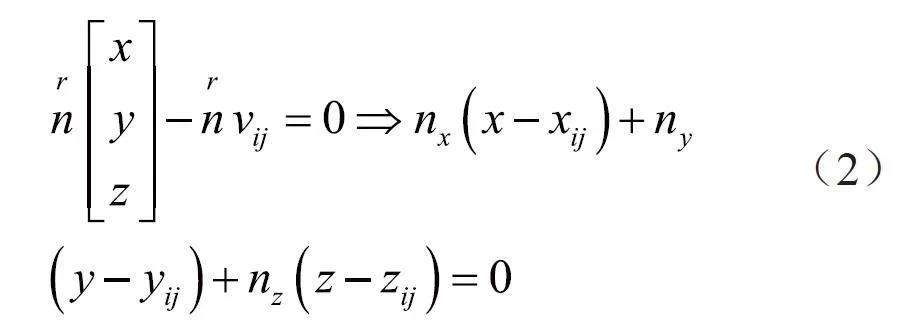
[摘 要]傳統的刀軌規劃方法基于經驗公式和手工計算,效率低下且難以保證加工精度,對此文章提出基于支持向量回歸的數控加工刀軌自動規劃方法。試驗結果表明,基于支持向量回歸的數控加工刀軌自動規劃方法可提高效率與加工精度,具有較高的實用價值。
[關鍵詞]刀軌自動規劃;數控加工;路徑規劃;支持向量回歸
[中圖分類號]D26.4 [文獻標志碼]A [文章編號]2095–6487(2024)04–0146–03
1 基于支持向量回歸的數控加工刀軌自動規劃方法的設計
1.1 提取數控加工刀具特征
在基于支持向量回歸(SVR)的數控加工刀軌自動規劃方法中,提取刀具特征是關鍵。這些特征需要根據加工任務、刀具類型和條件選擇,可能還需進行降維處理。提取的特征應與刀軌數據相對應,以便訓練SVR 模型來建立特征與刀軌參數之間的映射關系。
在數控加工中,經常使用的刀具包括平底刀、環形刀、球頭刀3 種類型。刀具參數如圖1 所示,其中環形刀的半徑為R,球頭刀與平底刀是環形刀的異形,當r=0 時為平底刀,當r=R 時為球頭刀。
計算數控加工代碼時,需考慮刀具類型和半徑對軌跡的影響。球頭刀因球心軌跡沿法矢方向偏移R 的特性,展現出良好的適應性和加工精度,且軌跡計算簡便。所以文章選擇球頭刀進行規劃分析,選取待加工的曲面s 等距刀軌半徑之間的距離得出一個刀位面s',其映射計算公式如下:
式中,Q為刀具軌跡所在超平面。
在刀位面上自動規劃刀具軌跡,可避免刀具間的相互干擾。刀位點即球頭銑刀的球心,位于被加工表面s 的刀位表面上。求解刀軌前需確定被加工面的刀面,并建立刀位面。基本思路為:將曲面上的三角形網格劃分為單元,沿面法矢方向求出等距刀軌半徑。
設定一三角面片Fi,其3 個頂點為vi=(vi0,vi1,vi2),頂點坐標為vij=(xij,yij,zij)(=0,1,2),該三角面片所在平面的表達式如式(2)所示:
刀具半徑為R 時,則頂點vij 所對應的刀位點的表達式如式(3)所示:
vij'=vij+R'n(3)
在提取了刀位面、點等特征之后,刀軌自動規劃方法可以利用這些特征來生成最優的刀具軌跡和切削參數,從而實現高效、精確的數控加工。
1.2 基于支持向量回歸構建刀軌預測模型
SVR 是一種用于解決回歸問題的監督學習算法,對噪聲和異常值具有較好的魯棒性。在數控編程中,刀具路徑的生成與規劃至關重要。為實現高效、精準的數控加工,需深入研究刀具路徑的生成和規劃。因此,研究選擇SVR 進行數控加工刀軌自動規劃設計。
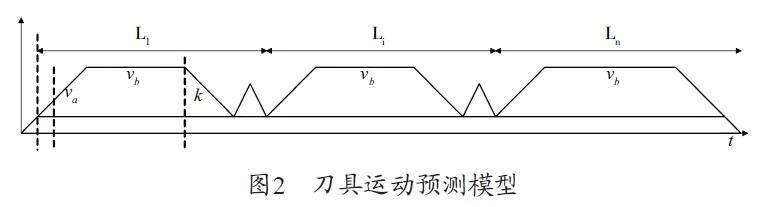
為了提升工作效率,刀具在規整的加工區域通常沿長度方向移動,如在狹長區域沿長軸移動,可顯著減少移動時間。SVR 算法的關鍵在于尋找一個最優超平面,該平面并非直接擬合數據,而是根據數據分布特點反映整體趨勢,然而,這一原理在復雜拓撲形狀上難以應用。因此,針對數控加工領域,構建一種簡化的刀軌預測模型。刀具運動預測模型如圖2所示。
在刀具加速階段va,數控加工能達到最大速度,加速度為k,在勻速切削狀態中,走刀速度為vb。
刀具軌跡理論上由刀體與加工表面嚙合關系確定,但受數控加工和表面表達方法的制約,通常以短直線段實現。走刀步長影響加工進度和效率:步長太大會降低精度,步長太小則會增加數據量,可能會引起速度波動,延長加工時間,影響效率和品質。因此,選擇合適的步長是刀具軌跡規劃的關鍵。
由于缺乏曲面局部區域的幾何拓撲信息,在開始計算時難以確定一個滿足精度要求的步長。因此,在沒有足夠的驅動點映射區域幾何拓撲信息的情況下,可以先設定一個初始步長l,其數值應小于刀具的直徑。滿足數控加工精度要求的步長l 的計算公式如下:
式中,R為有效切削刃的刀具半徑,α為加工局部區域的曲率半徑,β為允許加工誤差。
基于上述分析,文章設計的刀軌預測模型的表達式如下:
式中,D為切削間距,θ為刀具移行夾角。
當模型訓練完成后,可以將其應用于實際的刀軌預測中。通過輸入新的刀具信息、切削參數、工件材料信息等數據,模型可以預測出相應的刀具軌跡,為切削加工提供指導。
1.3 自動規劃并生成刀軌路徑
刀具路徑規劃算法的核心差異在于步長和行距計算方式。文章結合等殘留高度與變步長策略,提出新的刀具路徑規劃方法。該方法是一個循環迭代過程,包括同條軌跡和相鄰軌跡間刀位點數據的計算,可實現高效且精確的刀具路徑規劃。
文章設計的刀軌規劃算法的具體步驟如下。
(1)確定刀具的起始路徑位置,以最大的表面邊界為第一條刀位點的軌跡。
(2)對原始軌跡進行離散,由上述步驟得到一組滿足精度指標的刀位點。
(3)求出相應的刀位點,按行間距公式求出相應的刀位點。
(4)生成相近路徑,將每個相應的刀位點連接起來,擬合出的刀位點用來延長或剪裁所需的刀位點,使得它們的端點位于該曲面的邊界上,生成相鄰的刀位點軌跡。
(5)重復步驟(2)、(3)、(4),直至完全涵蓋數控加工處理區域。
(6)按照式(6),將刀位點轉化為刀觸點,然后按一定的次序進行聯接,即完成刀軌路徑的自動規劃。對于刀位點vij'(xq,yq,zq)轉換為刀觸點的計算公式如下:
式中, s 1為原始軌跡路徑長度, s 2為刀位點半徑長度。
2 試驗測試與分析
2.1 試驗準備
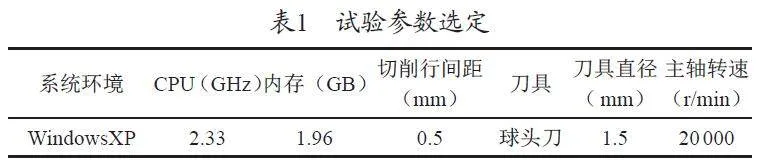
為驗證文章提出的基于支持向量回歸的數控加工刀軌自動規劃方法的有效性,本次測試以Matlab 軟件為試驗平臺,試驗參數選定見表1。
本次測試選擇一曲面的一條邊界線為刀具的初始路徑,使用文章所提方法對刀軌中的刀位點進行規劃,檢驗其與實際設定刀軌路徑是否吻合。
2.2 試驗結果與分析
基于上述試驗準備,在Matlab 軟件中建立了測試曲面,文章所提方法與實際的刀位點位置的測試結果見表2。
由表2 可知,基于支持向量回歸的數控加工刀軌自動規劃方法在試驗中表現出了良好的規劃性能。通過合理地選擇模型參數和切削參數,可以實現對刀軌路徑的準確預測,為數控加工過程提供有效的指導。然而,在實際應用中,還需要考慮更多的因素,如刀具磨損、材料特性等,以進一步提高刀軌規劃的準確性和魯棒性。
3 結束語
文章提出的基于支持向量回歸的數控加工刀軌自動規劃方法,利用機器學習技術實現智能、自動規劃。SVR能夠準確捕捉加工過程中的復雜非線性關系,生成更合理、高效的刀軌,提高加工質量、減少加工時間和能耗,并具有較好的泛化能力。然而,該方法仍面臨參數優化和模型泛化等挑戰。未來,將繼續深入研究,不斷優化和完善該方法,以期在數控加工領域實現更為廣泛的應用。
參考文獻
[1] 沈玉明,吳曉鳴,馮沛儒,等. 基于支持向量回歸代理模型的STATCOM 協同規劃方法[J]. 電工電能新技術,2023,42(10):66-73.
[2] 呂玉,辜桂香,聶江勇. 面向五軸數控加工刀軸運動控制的平滑控制算法研究[J]. 自動化與儀器儀表,2023(12):85-88.
[3] 陳波,葉玉全,王志標,等. 復雜槽輪零件數控加工工藝設計及仿真研究[J]. 內燃機與配件,2023(17):103-105.
[4] 王天力,劉威,范呂陽,等. 自由曲面等誤差數控加工刀軌生成方法[J]. 組合機床與自動化加工技術,2023(3):13-16.

