發掘數學文化，融入“閱讀與思考”欄目

摘 要：本文以三角函數與天文學為例，分析了數學文化融入“閱讀與思考”欄目的意義，揭示數學文化對學習的激勵作用，探討了數學文化融匯設計方法，以具體的教學活動設計為例，展示了如何將理論知識與實踐相結合，以實現提升學生學習興趣和數學文化素養的目標.

關鍵詞：三角函數；天文學；數學文化；教學活動

1 “閱讀與思考”欄目設計

1.1 背景意義

在高中階段設置“閱讀與思考”欄目，是一種創新的教育嘗試.以三角函數內容背景下的天文學材料為例，學生可以從中直觀地看到數學在現實世界，尤其是在解決復雜天文問題中的應用.天文學作為一個探索宇宙，尋找人類在宇宙中位置的學科，充滿了未知和神秘，能夠很好地吸引學生的注意力.通過學習天文學中的數學應用，學生不僅能獲得知識，還能被其中的探索精神所激勵，激發對數學研究的興趣.這樣的學習過程打破了數學在學生心中抽象、難以理解的刻板印象，增強了他們學習數學的動力和信心.［1］此外，在解決天文學問題的過程中，需要學生綜合運用所學的知識，將數學、物理等多個學科的知識交織在一起.這種跨學科的學習模式對于培養學生的綜合分析能力、解決問題能力以及創新思維能力都有重要意義.

1.2 閱讀材料案例

在天文學界，有一個謎題長久未解，即恒星距地球到底有多遠.這個問題像是廣袤宇宙對人類的挑戰.直到19世紀初，德國天文學家威廉姆·貝塞爾（Wilhelm Bessel）向它發起了挑戰.

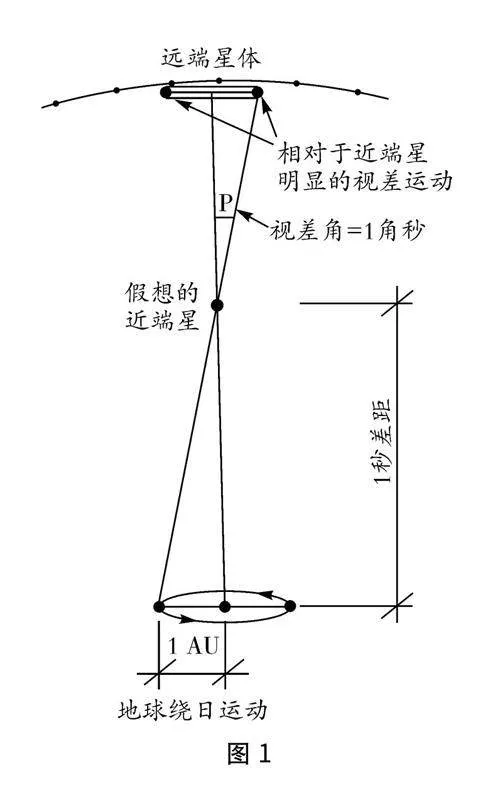
貝塞爾目光落在了一個名為天鵝座61的恒星上.這顆恒星因其相對地球的距離較近成為貝塞爾測量的理想目標.貝塞爾的策略是利用恒星視差（一種因觀察者位置變化引起的視差效應）.地球在太陽周圍的公轉，使得位于不同位置的觀察者看到近處的恒星相對于遠處背景星空位置發生的微小變化.貝塞爾計劃在一年中的兩個不同時間（相隔六個月，確保地球在公轉軌道的兩側）測量天鵝座61相對于更遠恒星的位置，從而捕捉到這一微小變化.要捕捉這種幾乎微不足道的變化，貝塞爾需要超越當時的技術極限，他使用了一種精密的測量儀器（赫歇爾式望遠鏡），并對其進行了改進，使其能夠進行更為精確的角度測量.通過長時間的觀測和記錄，貝塞爾收集了大量數據，這些數據需要他進行復雜、精細的計算.

貝塞爾將這些觀測數據帶入三角學的框架中.通過測量恒星在六個月間的視差角即恒星相對于地球在太陽軌道兩側位置的視線角度變化，貝塞爾能夠構建如圖1所示的一個簡單三角形，地球在其軌道上的兩個觀測點和恒星構成了這個三角形的頂點.利用基本的三角函數知識，他計算出了天鵝座61距離地球約10.4光年.

這一成就不僅是天文學史上的一座里程碑，也是人類首次觸摸到恒星距離的壯舉.貝塞爾的工作展示了三角學在解開宇宙奧秘中的強大力量，揭開了宇宙的一層神秘面紗，讓人類第一次準確地量度了恒星的距離，也為后世的天文學家提供了測量恒星距離的方法.貝塞爾的成就，不僅是一次科學上的突破，更是人類對宇宙探索的證明.

2 面向欄目的數學文化融匯設計

2.1 講述歷史發展故事

三角學與天文學的結合，是人類理解宇宙的一個重要里程碑.首先，教師介紹三角學的起源和發展，古巴比倫人和古希臘人是最早記錄和研究天體運動的文明，他們的工作為后來的三角學奠定了基礎.通過對這一時期的探討，學生可以了解到數學知識是如何在解決實際問題中誕生和發展的.其次，教師介紹阿拉伯學者在中世紀對三角學的貢獻，他們不僅保留了古希臘的數學文獻，還加以發展，將三角學推向了一個新的高度.最后，教師介紹歐洲文藝復興時期，天文學家和數學家利用三角學原理來支持和驗證他們的天文理論，展現數學與天文學交叉融合的魅力.通過這一系列歷史發展的介紹，學生不僅能夠了解到三角學的數學原理，還能夠深刻理解這些數學工具是如何在人類文明進步中發揮作用的.

2.2 走進數學家的生平

每一個數學概念的背后，都有一位或多位數學家的身影，他們的生平故事，不僅是數學歷史的一部分，更是激勵后人的寶貴財富.在“三角函數與天文學”的教學中，教師引入數學家的生平故事，可以讓學生更加生動地理解數學知識，感受數學家的智慧和創造力.以三角函數與天文學為例，教師可以帶領學生深入了解那些對這一領域做出重大貢獻的數學家和天文學家.例如，教師介紹希臘天文學家克羅狄斯·托勒密（Claudius Ptolemaeus）和他的《天文學大成》如何影響了后世對天體運動的理解；阿拉伯數學家阿爾·花剌子模（Al Xorazmiy）如何將希臘的三角學傳入阿拉伯世界并加以發展.在數學家生平的學習中，學生不僅能學習到數學和天文學的知識，還能從中汲取追求真理和勇于探索的精神動力.這種人文關懷的融入，使得數學學習變得更加吸引人和有意義.

2.3 發掘經典數學思想

數學知識的學習，不只是學生對公式和定理的記憶，更重要的是學生要理解其中蘊含的思想和方法.在“三角函數與天文學”的教學中，教師通過發掘和討論經典的數學思想，可以幫助學生深入理解數學概念，培養其抽象思維能力和創新能力.教師可以引導學生探討和發掘三角函數在天文學中應用的經典思想，即如何通過觀察和實驗來驗證理論，以及這些理論和實踐如何推動了人類對宇宙的理解和探索.通過分析貝塞爾測量恒星距離的方法，學生可以深入了解三角視差的概念，以及它是如何幫助人類首次準確測量出恒星距離的.此外，教師可以設置思考題和討論題，鼓勵學生思考如果沒有三角函數，人類會如何嘗試測量天體距離，以及三角函數在現代天文學中的應用.通過發掘經典數學思想，學生可以理解數學不僅是工具，更是一種思維方式.這種思維方式的培養，對學生的學習和未來的生活都具有重要意義.

3 教學活動設計

3.1 歷史場景復現

教學目標：構建基于歷史事件的真實問題場景，激發學生的好奇心和探索欲，引入知識點.

問題1 在廣袤的星系中存在著一顆恒星，你作為19世紀初一個知名的天文學家，通過大量的觀測，知道了它的周年視差是0.04′′，那么它到地球的距離是多遠？請自由分組，搜集關于“視差”“周年角位移”“天文單位”“角秒”和“秒差距”的概念，并利用三角視差法進行解答.

3.2 小組合作與探討

教學目標：促進學生之間的交流與合作，通過解決實際問題來深化對三角函數知識的理解.

（1）概念搜集.視差是從兩個不同位置觀察一個物體時，物體相對于背景的位置看起來發生變化的現象；周年角位移是指由于地球繞太陽公轉造成的，相對于遠處恒星背景的，一個近鄰恒星視位置的年度變化，這種變化形成了一個極小的角度，稱為周年視差；天文單位AU（Astronomical Unit）是一個長度單位，定義為地球到太陽的平均距離，它用于測量和表達太陽系內天體的距離；角秒是測量天文學中角度的單位，1角秒為13 600度；秒差距是天文學中用來測量星際距離的單位，一秒差距定義為當一個天體的年視差為一角秒時，該天體與觀測者之間的距離.

（2）問題解答.如圖2所示，BC代表八月地球到恒星的距離，BOBC=sin α，BC=BOsin α.

由∠P=0.04″，則α=0.02″，則BC=1 AUsin 0.02″ =50秒差距，由于1秒差距=3.26光年，則BC=50×3.26=163（光年）.

3.3 綜合提升與歸納

教學目標：通過測試和討論，檢驗和鞏固學生對三角函數知識的掌握，幫助學生總結知識點，提升解題能力.

問題2 函數f（x）=cos2x＋2sinxcosx，求出f（x）的最小正周期及單調遞減區間；求出f（x）在區間0，π4上的最值.

思路過程：利用二倍角公式與兩角和公式，將原式變化為f（x）=2sin2x＋π4，由周期性質得到最小正周期為π，繼而得到單調遞減區間為［π8＋kπ，5π8＋kπ］，k∈Z，故最大值為2，最小值為1.

歸納總結：教師總結本次教學活動的重點和難點，確保每位學生都能掌握關鍵知識點.

4 結語本文通過分析“三角函數與天文學”的實際案例，展現了數學文化融入“閱讀與思考”欄目的重要作用.數學文化的融匯設計不僅豐富了學生的數學知識，還拓寬了他們的視野，激發了學生對科學探索的熱情.［2］具體的教學活動設計能夠進一步加深學生對數學概念的理解，培養他們的綜合分析能力和創新思維.

參考文獻

［1］屈小妹，閆曉亭，陽均.數學文化融入初中數學翻轉課堂的研究與實踐——以平方差公式為例［J］.湖北師范大學學報（自然科學版），2024（1）：104-109.

［2］肖忠偉.新課標下初中數學閱讀思考型課堂的構建［J］.中學課程輔導，2023（25）：60-62.