引導聚焦基本圖形，變式追問成果擴大

摘 要：九年級相似三角形學習之后的復習課或習題課往往涉及與圓有關的相似問題.與其零星出現一兩道圓的問題，教師不如安排“相似學后再看圓”的專題課，帶領學生從相似的角度研究圓相關的基本圖形，進行變式設問，生成一系列與相似有關的同類問題，切實提升解題教學效益.

關鍵詞：基本圖形；相似；圓

《義務教育數學課程標準（2011年版）》和《義務教育數學課程標準（2022年版）》對“相似”“圓”的學習要求都不高，很多知識或定理的教學要求都是“了解”或“選學”級別.不少版本的初中數學教材將“圓”安排在九年級上冊，將“相似”安排在九年級下冊，這樣就使得九上學習圓時不會涉及與圓有關的相似問題，而九下學習相似時，又很少與圓結合起來.筆者曾檢索過人教版《義務教育教科書數學九年級下冊》，在“相似”一章中，僅章末練習中出現一道與圓的相交弦性質有關的相似習題；蘇科版《義務教育教科書數學九年級下冊》，在“相似”一章中，也只是在習題部分出現了兩道與圓有關的相似習題.為了引導學生從相似的視角看圓的一些基本圖形問題，筆者設計了一節“相似學后再看圓”的專題課，本文整理該課的教學設計，為廣大教師提供課例研討.

1 “相似學后再看圓”專題課教學設計@@教學環節1：從“垂徑定理”基本圖形出發.##

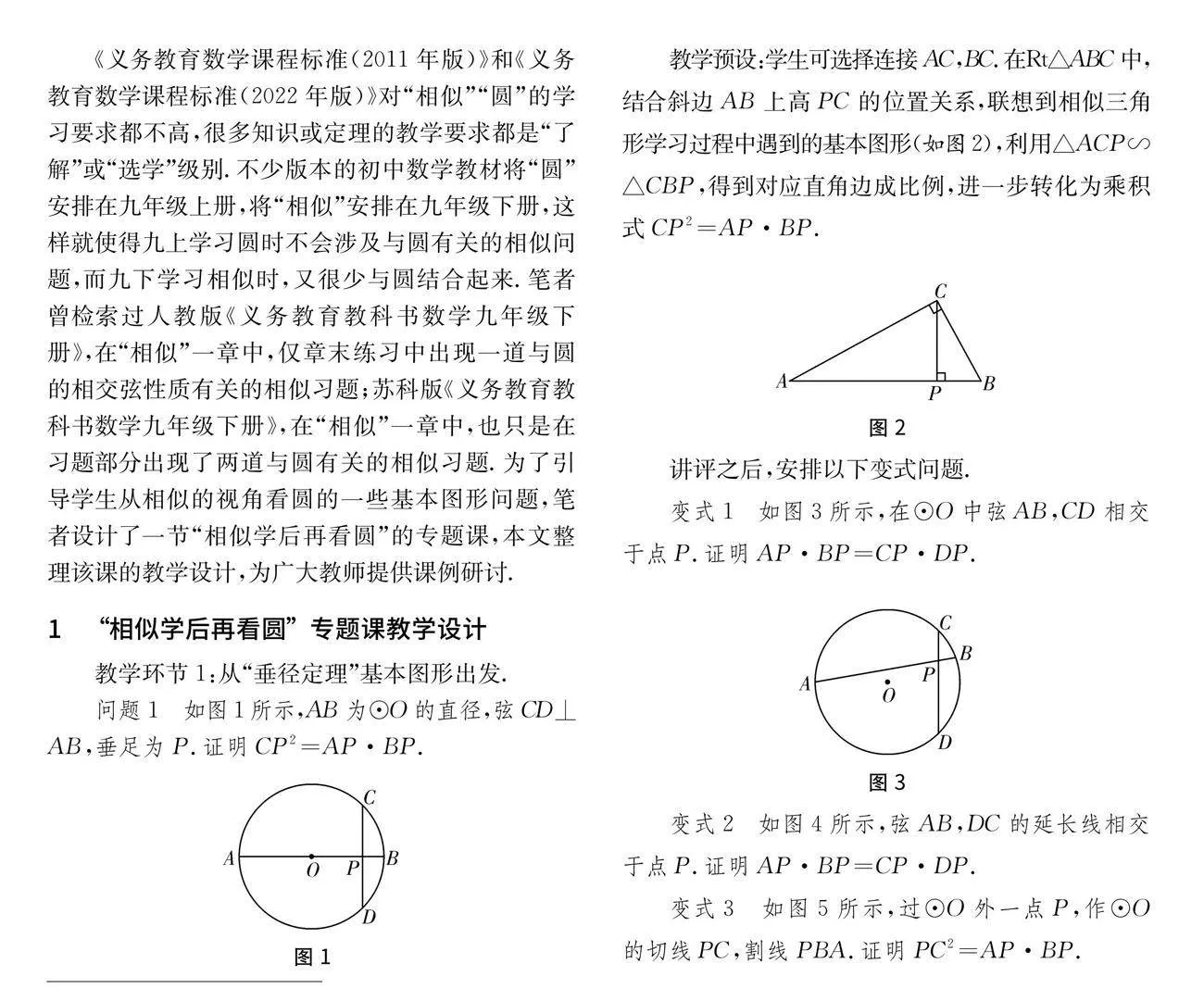
問題1 如圖1所示，AB為⊙O的直徑，弦CD⊥AB，垂足為P.證明CP2＝AP·BP.

教學預設：學生可選擇連接AC，BC.在Rt△ABC中，結合斜邊AB上高PC的位置關系，聯想到相似三角形學習過程中遇到的基本圖形（如圖2），利用△ACP∽△CBP，得到對應直角邊成比例，進一步轉化為乘積式CP2＝AP·BP.

講評之后，安排以下變式問題.

變式1 如圖3所示，在⊙O中弦AB，CD相交于點P.證明AP·BP＝CP·DP.

變式2 如圖4所示，弦AB，DC的延長線相交于點P.證明AP·BP＝CP·DP.

變式3 如圖5所示，過⊙O外一點P，作⊙O的切線PC，割線PBA.證明PC2＝AP·BP.

教學預設：這組變式立意體現了從特殊到一般再到特殊的過程.證明思路都是構造相似三角形.三道變式題講評之后，教師可在圖5的基礎上，作射線PO與⊙O相交于M，N兩點（如圖6），連接OC，設⊙O的半徑為r，點P到圓心O的距離為d，容易得到d2-r2＝PC2.同理，在圖4中，也可得到AP·BP＝CP·DP＝d2-r2.問題1及其變式的證明體現了“數學上統一的精神”

@@教學環節2：研究“垂徑定理”基本圖形.##

問題2 如圖7所示，AB為⊙O的直徑，弦CD⊥AB，垂足為P.連接AC，BC，BD，AD.證明AC·BD＋AD·BC＝AB·CD.

教學預設：考慮到垂徑定理基本圖形中具有很多軸對稱性質的線段，可以將相等的線段進行等量代換.待證等式的左邊AC·BD＋AD·BC＝AC·BC＋AC·BC＝2AC·BC.待證等式的右邊＝AB·CD＝AB·2CP＝2AB·CP.由△ABC∽△CBP，可得AC·BC＝AB·CP.可得，等式左邊=等式右邊，接通證明思路.另外，如果從四邊形ACBD是特殊的四邊形“箏形”來看，基于面積的角度“算兩次”也可證明.在講評上述方法之后，教師出示以下不同的證法，安排學生“閱讀理解”.

閱讀理解：如圖8所示，在AB上取一點E，連接EC，使∠ACE＝∠DCB，結合∠CAE＝∠CDB，可證△AEC∽△DBC，得比例式ACDC＝AEDB，化為乘積式AC·DB＝AE·CD①.

由∠ACE＝∠DCB，可得∠ACD＝∠ECB，結合∠ADC＝∠EBC，可證△ADC∽△EBC，得比例式 ADEB＝CDBC，化為乘積式AD·BC＝BE·CD②.

將①＋②，可得AC·DB＋AD·BC＝（AE＋BE）·CD，即AC·BD＋AD·BC＝AB·CD.

教學組織：學生在“閱讀理解”之后，教師可安排學生在小組內交流，簡述這種證明思路，然后每個小組推薦一名代表在組內詳細講解，教師抽一兩名學生上臺講解上述解法.講評之后，教師引導學生回顧反思，發現這種證明思路并不需要垂徑定理的特殊圖形，沒有使用直徑、垂徑弦等“強化條件”.教師引導學生猜測上述結論是否可以一般化，進而提出如下的挑戰問題.

教學環節3：拓展挑戰與同類再練.##

挑戰問題 如圖9所示，四邊形ABCD的四個頂點在同一個圓上，連接對角線AC，BD.證明AB·CD＋BC·AD＝AC·BD.

教學預設：學生結合上面的“閱讀理解”證明過程，發現挑戰問題的證明思路與其完全相同.在AC上取一點E，連接EB，使∠ABE＝∠DBC，分別“證兩次相似三角形”，得到兩組比例式轉化為對應的乘積式后再相加即可.教師鼓勵最先獲得思路的學生上臺展示交流自己的證明思路.教師總結歸納該問題的結論就是著名的“托勒密定理”.

同類練習1 如圖10所示，點P在等邊三角形ABC的外接圓上，連接PA，PB，PC.證明PB＋PC＝PA.

教學預設：根據“挑戰問題”的結論可知AB·CP＋AC·BP＝AP·BC.結合等邊三角形ABC的三邊相等，化簡可得PB＋PC＝PA.

同類練習2 如圖11所示，AB是⊙O的直徑，點C在圓上，CD平分∠ACB，交⊙O于點D，分析線段AC，BC，CD之間的數量關系，并說明理由.

教學預設：連接AD，BD，可先證出△ABD是等腰直角三角形，有AB＝2AD＝2BD.結合“挑戰問題”的結論可知AC·BD＋AD·BC＝AB·CD，簡化為AC＋BC＝2CD.

@@教學環節4：課堂小結，布置作業.##

教師引導學生總結發現本課是學習相似之后對與圓有關基本圖形的再認識，引導學生總結問題中涉及的基本圖形性質.

教師布置如下作業.

（1）題干條件同課上“問題1后的變式3”，當PC＝4，PB＝2時，求AB的長.

（2）題干條件同課上訓練的“同類練習2”，當⊙O的半徑為2，∠BAC＝30°時，求CD的長.（用兩種不同的方法）

（3）圍繞本課所學內容，選取某一個基本圖形問題的思路探究及“成果擴大”，整理成一篇解題隨筆.

2 教學立意的進一步解讀

2.1 精心選取基本圖形，變式追問成果擴大

李善良教授曾就“問題情境設計”提醒教師要“注重一境多用，讓學生形成整體的認識，防止出現一個內容一個情境、情境遍地開花的現象.”［1］在上文課例中，教師選取圓中“垂徑定理”基本圖形，從相似的角度探究基本圖形性質，并通過變式追問促進學生對該圖形的深刻理解，達到研究一個圖形，學會一類問題的教學目標.

2.2 深刻理解問題本質，概括性質應用鞏固

日本數學家、教育家米山國藏在《數學的精神、思想和方法》中曾提到“充滿在整個數學中的統一建設的精神”，并指出很多同類問題“無論表面上看來多么不同，都可用同樣的方法處理”.［2］在上文課例中，筆者基于圓的“垂徑定理”基本圖形提出一個圓內接四邊形的兩組對邊乘積之和等于兩條對角線之積的命題，先安排學生從相似或面積法的思路進行證明，隨后給出一個不同方法的“閱讀理解”，引導學生理解這種證明思路，并將命題概括為“一般化”的結論（即“托勒密定理”）.進一步安排兩個經典問題鞏固所學性質，并理解這類“形異質同”問題的解法具有一致性.

參考文獻

［1］李善良.高中數學課程改革：探索與實踐［M］.南京：江蘇教育出版社，2012.

［2］米山國藏.數學的精神、思想和方法［M］.上海：華東師范大學出版社，1986.