數學知識在高中物理解題中的應用探討

【摘要】物理學是一門以數學為基礎的學科，數學知識在高中物理解題中發揮著非常重要的作用.本文以線性關系、數列思想和均值不等式等數學知識為例，探討數學知識在高中物理中的應用，挖掘數學在解決物理問題中的重要作用．

【關鍵詞】數學知識；高中物理；解題技巧

1 線性關系在高中物理實驗中的應用

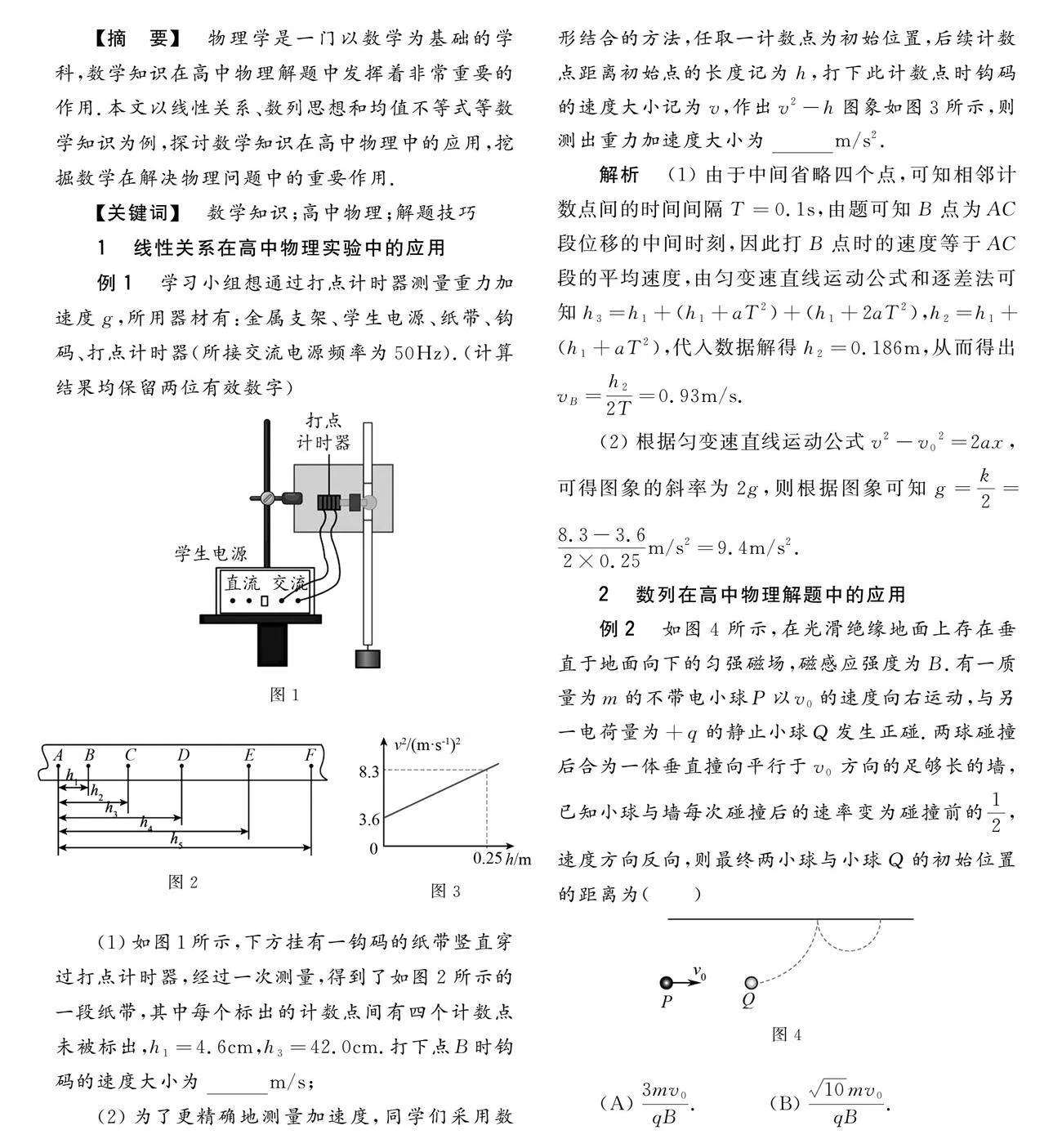
例1 學習小組想通過打點計時器測量重力加速度g，所用器材有：金屬支架、學生電源、紙帶、鉤碼、打點計時器（所接交流電源頻率為50Hz）．（計算結果均保留兩位有效數字）

（1）如圖1所示，下方掛有一鉤碼的紙帶豎直穿過打點計時器，經過一次測量，得到了如圖2所示的一段紙帶，其中每個標出的計數點間有四個計數點未被標出，h1 = 4.6cm，h3 = 42.0cm．打下點B時鉤碼的速度大小為 m/s；

（2）為了更精確地測量加速度，同學們采用數形結合的方法，任取一計數點為初始位置，后續計數點距離初始點的長度記為h，打下此計數點時鉤碼的速度大小記為v，作出v2-h圖象如圖3所示，則測出重力加速度大小為 m/s2．

解析 （1）由于中間省略四個點，可知相鄰計數點間的時間間隔T = 0.1s，由題可知B點為AC段位移的中間時刻，因此打B點時的速度等于AC段的平均速度，由勻變速直線運動公式和逐差法可知h3=h1+（h1+aT2）+（h1+2aT2），h2=h1+（h1+aT2），代入數據解得h2=0.186m，從而得出vB=h22T=0.93m/s．

（2）根據勻變速直線運動公式v2－v02=2ax，可得圖象的斜率為2g，則根據圖象可知g=k2=8.3－3.62×0.25m/s2=9.4m/s2．

2 數列在高中物理解題中的應用

例2 如圖4所示，在光滑絕緣地面上存在垂直于地面向下的勻強磁場，磁感應強度為B．有一質量為m的不帶電小球P以v0的速度向右運動，與另一電荷量為+q的靜止小球Q發生正碰．兩球碰撞后合為一體垂直撞向平行于v0方向的足夠長的墻，已知小球與墻每次碰撞后的速率變為碰撞前的12，速度方向反向，則最終兩小球與小球Q的初始位置的距離為（ ）

（A）3mv0qB． （B）10mv0qB．

（C）2mv0qB．（D）5mv0qB．

解析 設小球Q的質量為M，兩球碰撞合為一體后的速度為v，根據動量守恒，有mv0=m+Mv，根據洛倫茲力提供向心力有qvB=M+mv2r，解得兩球碰撞合為一體后運動半徑r=mv0qB，由題意可知，小球與墻每次碰撞后的運動半徑變為碰撞前的12，所以在水平方向的距離為x=r+r+12r+14r+18r+…，利用等比數列求和公式可得x=3r，最后利用勾股定理可得最終兩小球與小球Q的初始位置的距離d=3r2+r2=10r=10mv0qB．故選（B）．

3 均值不等式在高中物理中的應用

例3 如圖5所示，固定斜面AB的底邊和高均為h，平臺和斜面頂點B在同一條水平線上，平臺右端點C在A的正上方．平臺左端豎直固定一擋板，一輕質彈簧左端固定在擋板上，自由端在O點．疊放的兩個小物體P和Q質量均為m，放在O點，P與平臺間的動摩擦因數為μ，把兩小物體向左推到D點無初速度釋放，P和Q之間無相對滑動，剛好運動到C點停止．已知CD間距離也為h，重力加速度為g．

（1）若把Q取下來放置在C點，把PeErGMYG8FmaLg+9UvIsf+fKnhpSGz4AzQSH4IY2vnd8=推到D點，由靜止釋放，兩物體發生碰撞（碰撞時間極短）并粘在一起拋出，求兩物塊離開平臺時的速度大小；

（2）若把Q取下來，并且把P推至不同位置無初速度釋放，求P落在斜面上時的最小速度大小．

解析 （1）設P、Q在D點時彈簧彈性勢能為Ep，根據功能關系可得Ep=μ·2mgh.

取下Q后，P在D點由靜止釋放，設運動到C點時的速度為vC，根據功能關系可得Ep=μmgh+12mvC2，

解得vC=2μgh.

碰撞過程，根據動量守恒可得mvC=2mv，

解得v=2μgh2．

（2）設P從C點離開時的速度為v0，根據題意可知v0的大小不同，P離開平臺后做平拋運動，根據平拋運動規律有y=12gt2，x=v0t，

又有x+y=h，

聯立可得v0=ht－12gt，

根據P在豎直方向做自由落體運動可知，落在斜面上時的豎直分速度為vy=gt，

設落在斜面上時P的速度為v，根據運動合成可得v2=v20+v2y，

整理得v2=（h2t2+5g24t2）－gh，

根據均值不等式可知h2t2+5g2·t24≥2h2t2·5g2·t24=5gh，

解得v的最小值為vmin=（5－1）gh．

4 結語

數學知識和方法在高中物理解題中具有廣泛的應用．通過深入挖掘數學在解決物理問題中的作用，可以更好地理解和掌握物理知識，提高解題效率．未來的研究可以進一步探討如何將數學思想與物理教學相結合，以提高教學效果．