基于Matlab線性規劃二次優化在鋼筋下料中的應用

摘要：以西渝高鐵某鋼筋加工廠鋼筋下料為背景，提出一種通過兩次優化過程，建立方案組合篩選和方案組合一維線性規劃模型，使得復雜的優化數學理論問題變得直觀易懂。該方法通過算例，利用計算機輔助計算軟件Matlab，將上述數學模型應用于施工現場，提高鋼筋下料計算效率和自動化程度，提升了材料的利用率，從而達到節約成本的目的，具有很強的實用性。

關鍵詞：一維線性規劃二次優化Matlab軟件成本控制

中圖分類號：O221.1;TU755.3

ApplicationofLinearProgrammingQuadraticOptimizationBasedonMATLAB

inRebarCutting

ZHANGZhongliang

The4thEngineeringCo.，Ltd.，ofChinaRailway20thBureauGroupCo.， Ltd.，QingdaoCity，ShandongProvince，266061China

Abstract：Inthispaper，basedontherebarcuttingprocessinareinforcingbarprocessingplantofXi’an-Chongqing（Xiyu）high-speedrailway，aquadraticoptimizationprocessisproposedtoestablishthemodelofschemecombinationscreeningandone-dimensionallinearprogrammingofschemecombination，makesthecomplexoptimizationofmathematicaltheoryproblems becomeintuitiveandeasytounderstand.Themethodappliestheabovemathematicalmodeltotheconstructionsitebymeansofanexampleandthecomputer-aidedcalculationsoftwareMATLAB，whichimprovesthecalculationefficiencyandautomationdegreeofrebarcuttingandtheutilizationratioofmaterials，achievingthepurposeofcost-saving，whichstrongpracticality.

KeyWords：One-dimensionallinearprogramming;Quadraticoptimization;Matlabsoftware;Costcontrol

西渝高鐵作為我國重要的在建高鐵項目，在我國的交通運輸中發揮著重要作用。鋼材作為鐵路建設中的重要物資，在成本控制中占據重要的地位。以某標段為例，正線長度30km，鋼材使用量為10.2萬t，其中鋼筋為4.19萬t，占比95.2%。鋼筋下料是鋼筋加工的重要環節，通常鋼筋下料人工憑經驗完成，不僅耗時，鋼筋利用率不高，使得企業的經濟效益降低。鋼筋優化下料就是通過對大量待加工鋼筋進行篩選比較、優化組合，達到更多地節省鋼筋原材料的目的，其優化目標值是使用的鋼筋原料最少。鋼筋優化下料問題是個典型的一維優化組合問題。對于小規模下料，通過方案組合篩選，線性規劃的方式在施工現場鋼筋下料中具有很好適用性。

1需求分析及數學模型

長度常為12m或9m，此種鋼筋常作為主筋使用，下料長度不定，最短的長度常在0.8m以上，也就是說0.8m以下的鋼材有可能作為余料丟棄，以余料為0.8m為例，鋼筋利用率為（9-0.8）/9=91.11％，存在巨大的改進空間。因此通過鋼筋的優化組合使鋼筋的利用率提高主要是針對定長鋼筋，也即是本文要討論的對象。

本文討論的對象忽略切口影響。需求的定義示例如下：設單根的定長鋼筋長度為L，在此中鋼筋上裁剪長度分別為a1、a2、a3的半成品，一根線材上所下的3種半成品的數量為x1、x2，x3，分割的公式可表示為

a1x1+a2x2+a3x3≤L

半成品的切割方式向量為x（x1，x2，x3），半成品向量為l（x1，x2，x3），即在長度為L的鋼筋上切割x1個a1，x2個a2，x3個a3個。由于訂單要求的半成品的長度有多種可能的組合，下料的方式也可能有好多種。

決策變量：用xj表示按照第j種切割方式所使用的鋼筋根數，明顯xj是非負的整數，用xij表示按照第j種切割方式，一根線材所切割下來的第j種需求坯料的數量。

其中矩陣A，矩陣X代表每一種分割方案對應采用的數目，矩陣b不等式約束的資源數。

2數學模型求解

2.1計算步驟

Step1：導入下料長度表，包含半成品種類、長度、數量，能夠接受的余料的長度[3]。

Step2：求解單根原材生產對應生產的某種半成品最大值。

Step3：枚舉法計算列出不同的下料方案，根據方案篩選器和余料調節器，篩選出方案余料的接受值，并選擇滿足條件的所有的方案組合。

Step4：方案矩陣轉置，列出目標函數及約束條件，轉換成Matlab可以接受的基本型。

Step5：利用軟件根據約束條件，目標函數計算每種下料方案的循環次數及方案組合。

Step6：輸出下料長表（包含方案循環次數、下料長度、數量、材料利用率、余料長度等）。

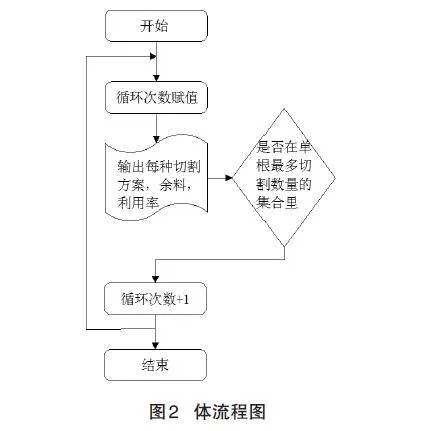
2.2評價指標及流程圖

生產中常用的評價指標為鋼筋的利用率，其公式[3]為：

• 編程實現及算例

本文采用φ22的螺紋鋼為例，首先進行方案篩選及余料調節，原材料長度為L=9000mm。

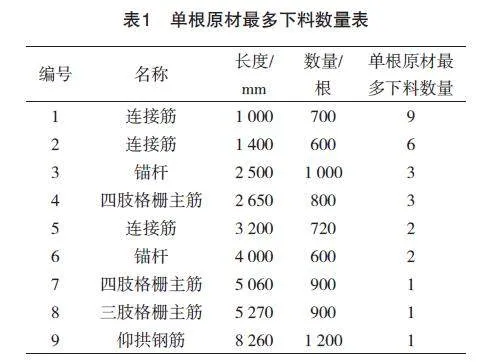
首先按照鋼筋長度進行排序，以下料長度為計算對象，計算單根原材最多下料數量，如表1所示[5]。

以上述表中的單根原材最多下料數量作為方案的迭代次數的運行條件，程序實現如下：

i=0;

forx1=0：9

forx2=0：6...........forx9=0：1

r=9-x1*x1+1.4*x2+2.5*x3+2.65*x4+3.2*x5+4*x6+5.06*x7+5.27*x8+8.26*x9）;

if（r>=0）&&amp;（r<1）

if（r<0.1）%余料長度調節器

number=number+1;

fprintf（'%3d%3d%3d%3d%3d%3d%3d%3d%3d%3d%3d%3d＼n'，number，x1，x2，x3，x4，x5，x6，x7，x8，x9，r，（9-r）/9*100）;

............

end

end

上述過程中當余料長度調節器分別設定0.74、0.5、0.3、0.2、0.1時所有的組合數量分別為57、39、26、24、15；最大的一種材料長度為8.26m，只能生產一種，余料為0.74m；其他方案產生的余料長度不是最優化的長度。故此時包含了第一次的優化篩選，本篩選滿足的條件有兩個：第一，保證余料為設定的理想值[4]；第二，保證方案選項中包含生產所有的半成品料。本例中設定的余料接受值為0.1m，而此時沒有包含生產8.26m的方案，故在最后的條件中加入，這樣就能滿足上述兩個條件。由上得出第一次優化篩選小于0.1m的方案組合的矩陣。

將上述方案得出矩陣進行轉置，并將目標函數及約束條件轉化成標準型，帶入程序實現。

程序如下：

clc，clear;

f=[1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1];%目標函數

A=[*******************];%方案矩陣

b=[-700，-600，-1000，-800，-720，-600，-900，-900，-1200];%b

lb=zeros（16，1）;

intcon=[1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16];

[x，fval]=intlinprog（f，intcon，A，b，[]，[]，lb，[]）;%整數型線性規劃

x，fval=fval

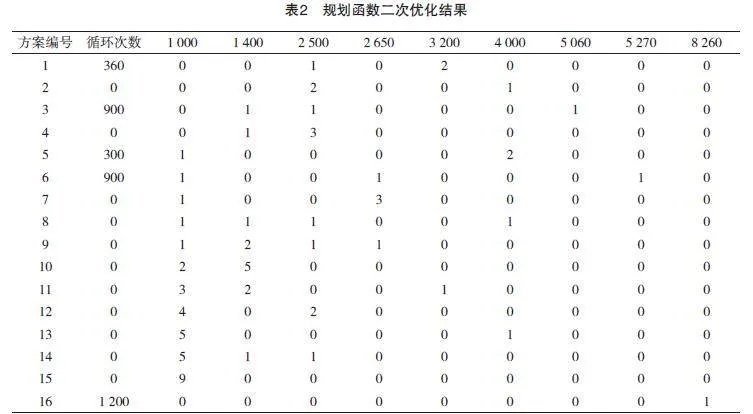
至此通過規劃函數進行了第二次優化。計算結果如表2所示。

通過優化得出如下結果：方案1加工次數：360次，余料長度360×0.1m，利用率98.9%；方案3加工次數為：900次余料長度為900根×0.04m，利用率：99.6％；方案5加工次數為：300次余料長度為0，利用率：100％；方案6加工次數：900次，余料長度900根×0.08m，利用率：99.6％；方案16加工次數：1200次，余料長度1200根×0.74m，利用率：91.77％.目標函數原材利用數量為3660根，綜合利用率為：（360×98.9%+900×99.6％+300×100％+900×99.6％+1200×91.77％）/3660=96.99％.最后一種余料長度為0.74m，可以進入下一批次的優化，以取得更好的材料利用率。

4結語

本文通過在對本標段鋼構廠進行實踐，取得了良好的效果，建立的一維下料的數學模型，利用Matlab進行數據處理，通過一次余料優化，篩選余料最少的方案組合。二次優化通過利用整型規劃函數進行優化，得出方案最佳組合，從而給定本批次的局部的下料組合。使得鋼筋原材數量最少，有效地導鋼筋下料，達到節約成本的目的，取得了良好的經濟效益，具有很強的可推廣性。

參考文獻

[1]馬浩.F型鋼一維下料的優化算法[J].山西建筑，2023，49（23）：149-150.

[2]田飛，符學勇.基于線性規劃模型鋼材下料問題最優切割方案研究[J].科學技術創新，2023，（23）：194-198.

[3]錢輝.建筑工程鋼筋下料優化分析方法及軟件開發[D].南昌：南昌大學，2023.

[4]王朝暉，曹陽.整數規劃近似算法在鋼筋下料中的應用研究[C]//中國建設科技集團股份有限公司，中國建筑學會工程總承包專業委員會，中國中建設計集團有限公司等.第二屆工程總承包項目管理經驗交流會暨2019中國建筑學會工程總承包專業委員會年會論文集.中國建筑第五工程局有限公司，2019：5.

[5]萬書霞.某項目鋼筋工程數字化及下料優化研究[D].邯鄲：河北工程大學，2021.