你會解握手問題嗎

小朋友，在生活中，握手是我們社交時的一種禮儀。在數學中，有一類問題是和握手有關的，我們一起來看一下吧！

例題1東東參加夏令營活動時結交了5 名新朋友。他們初次見面時，每兩人都握了一次手。他們一共握了多少次手？

我們可以畫圖來分析，如圖1所示，把東東的5名新朋友分別用①②③④⑤來表示。題目要求每兩人都握一次手，東東應與5名朋友分別握手一次，他共握了5次。①已經與東東握過一次手，還要與②③④⑤分別握手一次，①又握了4次。同理，②還要握3次，③還要握2次，④還要握1次。他們一共握了5+4+3+2+1=15（次）手。

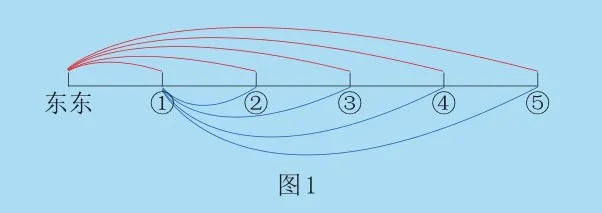
小朋友，若有m人，每兩人握手一次，是否有計算公式呢？我們不妨來找一找規律。

如圖2所示，若有2人，他們握手的次數總和是1次；若有 3人，他們握手的次數總和是1+2=3（次）；若有4人，他們握手的次數總和是1+2+3=6（次）。

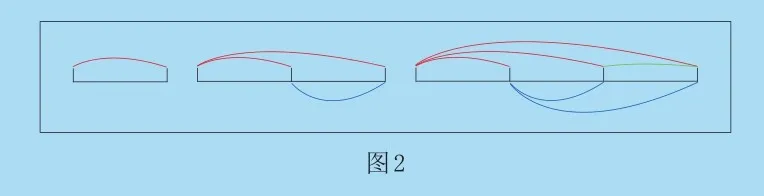
按照圖2中的規律可知，若有m人，他們握手的次數總和是從1開始一直加到（m-1），可算出總和是m×（m-1）÷2。把得出的公式用文字表述，可知握手次數=人數×（人數-1）÷2。

例題2學校要組織一次足球比賽，賽制為單循環形式（每兩支參賽隊之間都賽一場），一共要進行28場比賽。問參賽的球隊共有多少支？

比賽時每兩支參賽隊之間都賽一場，類比握手問題的公式得出“比賽的總場數=球隊支數×（球隊支數-1）÷2”，所以“球隊支數×（球隊支數-1）=比賽的總場數×2”。因為比賽的總場數是28場，所以球隊支數×（球隊支數-1）=28×2=56，又因為8×7=56，所以參賽的球隊有8支。

小朋友，像比賽中的單循環賽、設計一列火車的車票種類等都與握手問題是同樣的解法。你學會了嗎？