永磁同步電機電流環的二自由度內模控制

摘 要：目前工業上在對永磁同步電機（permanent magnetic synchronous motor， PMSM）進行控制時，常認為電流環的調節過程遠快于轉速環的調節過程，進而忽略電流環中反電動勢擾動項的變化。但對于采用PI控制且機械時間常數與電磁時間常數相差不大或更小的電機而言，若直接對電流環中的反電動勢擾動項進行忽略，將會導致電機的動態響應性能惡化。為解決上述問題，本文首先建立了永磁同步電機調速系統的數學模型，并根據此數學模型推導了PI控制條件下電機動態性能變差的原因，以及反電動勢擾動項能否進行忽略的條件，針對無法忽略的情況本文在傳統內模控制的基礎之上設計了一種二自由度內模控制器，該控制器具有2個可獨立調節的參數，可分別調節電流環的跟蹤特性與魯棒特性和抗干擾特性。最后，利用Matlab/Simulink對所設計的二自由度內模控制器與傳統的PI控制器進行對比仿真實驗。結果表明，相比于PI控制器，所設計的二自由度內模控制器使電流環具有更好的跟蹤性和魯棒性，解決了特殊情況下電機動態響應性能變差的問題。

關鍵詞：永磁同步電機（PMSM）；電流環；動態特性；內模控制；魯棒性

中圖分類號：TM301.2 DOI：10.16375/j.cnki.cn45-1395/t.2024.04.010

0 引言

由于永磁同步電機（permanent magnetic synchronous motor， PMSM）具有功率密度高、調速范圍廣等優點，使得以其為核心的伺服系統在工業領域中具有廣泛的應用[1-3]。為了使控制系統具有更好的動態性能，常使用雙閉環矢量控制的方式對永磁同步電機進行控制，其中電流環是系統高動態性能的關鍵，電流環的動態響應性能直接影響整個系統的動態響應性能[4]。在對永磁同步電機的電流環進行研究時，常假設電流變化時反電動勢近似不變，進而將電流環等效為一階慣性環節[5-6]。但當電機的機械時間常數小于或者等于電磁時間常數時，若仍認為反電動勢近似不變來控制電機，將會導致電流環的輸出難以跟上輸入，使得電機無法滿足高響應能力的控制系統。而永磁同步電機的機械時間常數反映的是電機轉速從靜止狀態達到穩定工作狀態所需的時間，在一些對電機反應速度要求較高的場合，如：飛行器、無人車、機器人關節轉軸等，常會選用機械時間常數較小的電機[7]。

為了解決永磁同步電機機械時間常數小于或者等于電磁時間常數時，PI控制能力不足的問題，文獻[8]提出了一種“PII控制器”，即仍將電流環等效為一階慣性環節，但在傳統的PI控制基礎上增加了一個積分環節來消除系統的穩態誤差。這種方法最終在理論上做到了電流環對給定信號的無誤差，但此方法對電機參數的變化十分敏感，當參數調節不合適時，系統響應不僅會變差甚至系統會ZCaKkeu9t/Gc5Niqpjabyzyklc9ykv6PXWRMh9OV/Uw=有被損壞的風險。文獻[9-10]采用了一種前饋補償的方法，即給系統引入了一項與反電動勢大小相同、符號相反的信號，進而抵消了反電動勢對系統的影響，使系統等效為一階慣性環節而動態特性良好。但這種方式需要采集電機的磁鏈和轉速作為已知參數，而電機的磁鏈和轉速均屬于時變參數。由于采樣延時等時滯因素的影響會使得到的參數有一定的誤差，所以這種方式最終取得的效果也不理想。文獻[11]介紹了一種內模控制方式，其具有原理簡單、實用性強等優點，在合適的控制參數下可使得系統具有良好的目標跟蹤特性、抗干擾特性和魯棒性，適合對電機這種干擾性強、參數時變的系統進行控制。但傳統的內模控制只有一個可調參數，調節時需要在跟蹤特性和抗干擾特性之間進行抉擇，顧此失彼，所以其控制效果并不完美[12-13]。

本文參考文獻[14]提出的二自由度內模控制方法，將此方法應用于PMSM的電流環控制之中，并在Matlab/Simulink中做了與傳統PI控制的性能對比試驗。最終結果表明：二自由度內模控制不僅解決了傳統內模控制調參難以取舍的問題，并且其控制效果明顯優于PI控制，解決了電流環動態性能惡化的問題。

1 PMSM調速系統的數學模型

1.1 PMSM的數學模型

PMSM是一種非線性、多變量的系統，其在自然坐標系下建立的數學模型具有復雜、多變量、強耦合的特點[15]。為了便于控制，采用矢量控制坐標變換的方式對其數學模型進行解耦和降階。本文給出了永磁同步電機在d-q同步旋轉坐標系下的數學模型。

假設三相PMSM為理想電機，做出如下假定[16]：

①忽略鐵心飽和；②不計渦流和磁滯損耗；③轉子上無阻尼繞組，永磁體不計阻尼作用；④相繞組中感應電動勢波形是正弦波。

其在d-q旋轉坐標系下對應的電壓方程為

[Ud=RId+LddIddt-ωeLqIq，Uq=RIq+LqdIqdt+ωe（LdId+ψf）.] （1）

電磁轉矩方程為

[Te=32PnIq[Id（Ld-Lq）+ψf]，] （2）

式中：[Ud、Uq]為[d、q]軸電壓；[Id、Iq]為[d、q]軸電流；[Ld、Lq]為[d、q]軸電感；[R]為定子的電阻；t為時間；[ωe]為電機的電角速度；[ψf]為永磁體的磁鏈；[Te]為電磁轉矩；[Pn]為轉子的極對數。

由式（1）可知，[d、q]軸的電壓方程仍存在相互耦合的感應電動勢項。為使后續工作方便，將耦合項當作擾動項進行處理，令：[Ud0=Ud+ωeLqIq，]

[Uq0=Uq-ωe（LdId+ψf）]，式（1）變為如下形式：

[Ud0=RId+LddIddt，Uq0=RIq+LqdIqdt.] （3）

式（1）中的同步旋轉坐標系具有如下規定：其d軸始終與轉子總磁鏈矢量[ψf]的方向重合，稱之為直軸，這個方向的電流分量主要是產生勵磁的作用；在d軸的方向上逆時針旋轉90°便是q軸的方向，稱之為交軸，此方向的電流分量主要產生轉矩的作用。

當PMSM的轉子類型為表貼式時，有：[Ld=Lq=L]。由式（2）知，此時d軸電流對轉矩的產生并無貢獻，為使在相同轉矩條件下所需的電流最小，采用[Id=0]的控制策略。在此條件下，式（2）、式（3）變為如下形式：

電壓方程為

[Ud0=RId+LdIddt=0，Uq0=RIq+LdIqdt=Uq-ωeψf.] （4）

電磁轉矩方程為

[Te=32PnIqψf.] （5）

由運動學公式得其運動方程為

[dωmdtτ=Te0-Bωm，] （6）

式中：[ωm]為電機的機械轉速；[τ]為電機的轉動慣量；[Te0=Te-Tl]，[Tl]為負載轉矩；[B]為電機的摩擦系數。

對式（4）和式（6）進行拉普拉斯變換，得到其對應的復頻域方程為

[Gc（s）=Iq（s）Uq0（s）=Id（s）Ud0（s）=1Ls+R，] （7）

[Gs（s）=ωm（s）Te0（s）=1τs+B]， （8）

式中：[Gc]、[Gs]分別為電流環和速度環電機部分的傳遞函數。

1.2 逆變器的數學模型

永磁同步電機的控制過程中常使用空間矢量PWM（space vector PWM， SVPWM）技術來控制三相逆變器，進而將直流電壓轉化為所需的交流電壓。SVPWM的理論基礎是平均值等效原理，即在一個開關周期內通過對基本電壓矢量加以組合，使其平均值與給定電壓矢量相等[17]。其工作過程為：首先，根據旋轉矢量在兩相靜止坐標系下的分量判斷其所處的扇區；然后，根據平均值等效原理計算出所在扇區主副矢量的作用時間，將其在一個開關周期內進行合理的分配并轉換為對應的PWM信號，進而控制逆變器的開關。

基于SVPWM算法控制的逆變器可將其等效為一階慣性環節，

[Ginv（s）=1Tss+1，] （9）

式中：[Ts]為逆變器的開關周期；因為逆變器的輸出與輸入相等，因此增益取1。

再考慮到開關延時、死區時間和數字控制延時的影響，將這些影響共同等效為一個延遲環節[e-sTd][ ][18]。因為[Td?Ts]（[Td]為開關延時、死區時間和數字控制延時的時間總和），故可將此延遲環節按照泰勒級數近似展開為一個一階慣性環節。綜上，考慮延遲和死區時間的SVPWM電壓源逆變器傳遞函數為[19]

[Ginv_d（s）=1（Tds+1）（Tss+1）.] （10）

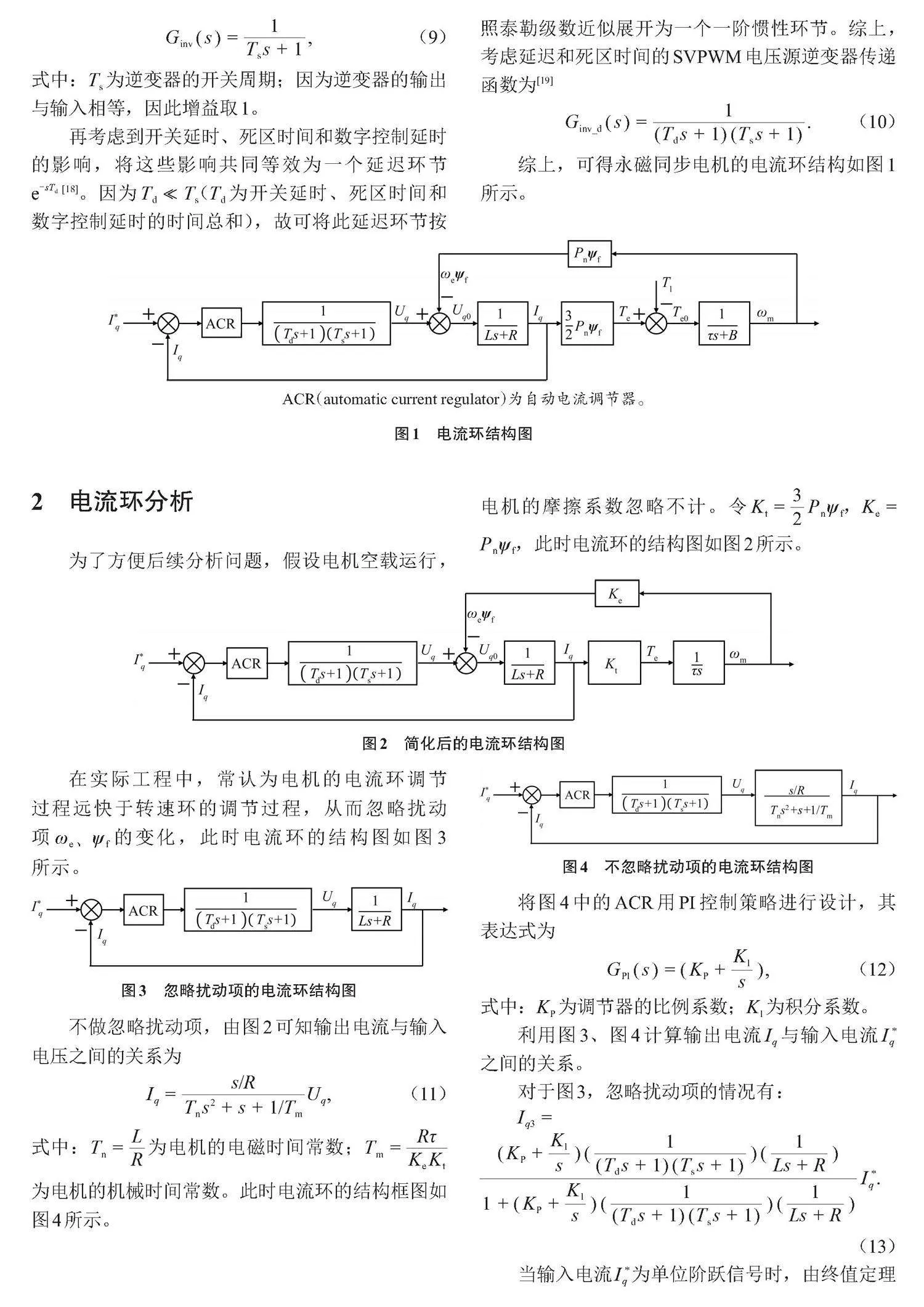
綜上，可得永磁同步電機的電流環結構如圖1所示。

2 電流環分析

為了方便后續分析問題，假設電機空載運行，電機的摩擦系數忽略不計。令[Kt=32Pnψf，Ke=Pnψf]，此時電流環的結構圖如圖2所示。

在實際工程中，常認為電機的電流環調節過程遠快于轉速環的調節過程，從而忽略擾動項[ωe、ψf]的變化，此時電流環的結構圖如圖3所示。

不做忽略擾動項，由圖2可知輸出電流與輸入電壓之間的關系為

[Iq=P/KxYDJs05bM0Iju/WKmmBX6wUXF14+T/ZIZXx8jA8A=s/RTns2+s+1/TmUq，] （11）

式中：[Tn=LR]為電機的電磁時間常數；[Tm=RτKeKt]為電機的機械時間常數。此時電流環的結構框圖如圖4所示。

將圖4中的ACR用PI控制策略進行設計，其表達式為

[GPI（s）=（KP+KIs），] （12）

式中：[KP]為調節器的比例系數；[KI]為積分系數。

利用圖3、圖4計算輸出電流[Iq]與輸入電流[I*q]之間的關系。

對于圖3，忽略擾動項的情況有：

[Iq3=（KP+KIs）（1（Tds+1）（Tss+1））（1Ls+R）1+（KP+KIs）（1（Tds+1）（Tss+1））（1Ls+R）I*q.] （13）

當輸入電流[I*q]為單位階躍信號時，由終值定理可求得輸出[Iq3]為

[Iq3=1.] （14）

可知此時輸入等于輸出，為理想情況，不存在穩態誤差。

對于圖4，不忽略擾動項的情況有：[Iq4=（KP+KI/s）（1（Tds+1）（Tss+1））（s/RTns2+s+1/Tm）1+（KP+KI/s）（1（Tds+1）（Tss+1））（s/RTns2+s+1/Tm）I*q.] （15）

同理，當輸入電流[I*q]為單位階躍信號時，由終值定理可求得輸出[Iq4]為

[Iq4=limt→∞（KP+KI/s）（1（Tds+1）（Tss+1））（s/RTns2+s+1/Tm）1+（KP+KI/s）（1（Tds+1）（Tss+1））（s/RTns2+s+1/Tm）I*q=lims→0（KP+KI/s）（1（Tds+1）（Tss+1））（s/RTns2+s+1/Tm）1+（KP+KI/s）（1（Tds+1）（Tss+1））（s/RTns2+s+1/Tm）·s·1s=lims→0（KI/s）·1·（s/R）·Tm1+（KI/s）·1·（s/R）·Tm=KITmR+KITm.] （16）

可知此時輸入與輸出并不一定相等，存在穩態誤差[EIq4]，

[EIq4=RR+KITm.] （17）

由式（14）和式（16）可得，并不是在任何情況下都可以忽略擾動項。對圖4中前向通道的第三項進行分析：

[s/RTns2+s+1/Tm=1/RTns+1+1/（Tms）→s=jωc][ 1/RTnjωc-j/（Tmωc）+1，] （18）

式中，j=[-1]。當[Tnωc?1Tmωc]時，可忽略[1Tmωc]項，其中[ωc]為系統的截止頻率，即

[Tnωc>10Tmωc?ωc>31TnTm.] （19）

當式（19）滿足時，式（18）有如下形式：

[s/RTns2+s+1/Tm=1/RTns+1=1Ls+R.] （20）

此時圖3與圖4的傳遞函數完全相同。因此，式（19）便是能否忽略擾動項的條件。

對于一般的傳遞系統，機械時間常數遠大于電磁時間常數，式（19）的條件一定滿足，此時可以對擾動項進行忽略。對于小轉動慣量的系統，因其機械時間常數與電磁時間常數相當甚至小于電磁時間常數，此時擾動項勢必會對電流環造成影響，應采取措施消除影響。

3 電流環內模控制器設計

內模控制是為受控對象并聯一個理想的數學模型，將實際輸出與理想輸出的差值反饋至控制器的輸入端，從而起到抑制模型失配、參數攝動以及外界干擾的作用，進而提高系統的魯棒性[20]。

3.1 內模控制原理

傳統的內模控制系統結構圖如圖5所示。

其中[r（s）、d（s）]和[y（s）]分別為系統的輸入、干擾和輸出信號；[u（s）]為內模控制器的輸出；[Q（s）]為內模控制器；[P（s）]為實際被控對象；[M（s）]為被控對象的理想數學模型。當圖5中受控對象的模型建立精確，即[P（s）=M（s）]時，[Q（s）]調節的是[d（s）]引起的誤差。當[P（s）]的參數發生攝動，[Q（s）]會對由干擾和參數變化引起的誤差進行共同調節。所以內模控制可以抑制因系統的模型失配、參數攝動而帶來的影響，能夠提高系統的魯棒性。

對圖5的結構進行簡化，得到圖6。

圖6中[C（s）]為

[C（s）=Q（s）1-Q（s）M（s）.] （21）

此時輸出[y（s）]與輸入[r（s）]之間的關系為

[y（s）=C（s）P（s）1+C（s）P（s）r（s）.] （22）

輸出[y（s）]與擾動[d（s）]之間的關系為

[y（s）=11+C（s）P（s）d（s）.] （23）

聯立式（21）、式（22）和式（23），可得

[y（s）=Q（s）P（s）1+Q（s）[P（s）-M（s）]r（s）+]

[1-Q（s）M（s）1+Q（s）[P（s）-M（s）]d（s）.] （24）

由式（24）可知，如果被控對象的實際數學模型和理想數學模型完全相同，即[P（s）=M（s）]，則式（24）具有如下形式：

[y（s）=Q（s）P（s）r（s）+[1-Q（s）M（s）]d（s）.] （25）

此時取[Q（s）=M（s）-1]，則

[y（s）=r（s）.] （26）

式（26）便是內模控制理想情況下的控制效果，此時輸出[y（s）]始終等于輸入[r（s）]。但實際情況下建立的數學模型并不能完全描述受控對象，為使式（26）可實現，通常會在內模控制器中加入低通濾波器[F（s）][ ][21]。

此時內模控制器具有如下形式：

[Q（s）=M（s）-1F（s）.] （27）

其中低通濾波器[F（s）]具有如下形式：

[F（s）=1（βs+1）m，] （28）

式中：[β]用于調節控制器的抗干擾性能；[m]為正整數，用于補償抗干擾控制器[Q（s）]的相對階，從而使系統可實現[22]。

聯立式（25）、式（27）和式（28）可得

[y（s）=1（βs+1）mr（s）+[1-1（βs+1）m]d（s）.] （29）

由式（29）可知參數[β]與系統的目標值跟蹤特性和干擾抑制特性、魯棒性均有關系。整定參數時需要在這些重要的特性之間進行取舍，易顧此失彼，這正是傳統內模控制只有一個自由度的不足之處。

3.2 二自由度內模控制器設計

圖7為二自由度內模控制器的簡化結構圖。

圖7由圖6推演而來。結合圖6，根據圖7可得

[y（s）=Q1（s）Q2（s）P（s）1+Q2（s）[P（s）-M（s）]r（s）+]

[1-Q2（s）M（s）1+Q2（s）[P（s）-M（s）]d（s）.] （30）

當控制器中加入低通濾波器，認為[P（s）=M（s）]，此時有

[y（s）=Q1（s）Q2（s）P（s）r（s）+[1-Q2（s）M（s）]d（s）].

（31）

仍然將[Q2（s）]用上述方式進行設計：

[Q2（s）=M（s）-1F2（s），F2（s）=1（βs+1）m.] （32）

聯立式（31）和式（32），有

[y（s）=Q1（s）F2（s）r（s）+[1-F2（s）]d（s）.] （33）

對[Q1（s）]進行如下設計，

[Q1（s）=F2（s）-1F1（s），F1（s）=1（αs+1）n，] （34）

式中：[α]為控制器的可調節參數；[n]為正整數，用于補償控制器[Q1（s）]的相對階，從而使系統可實現。

將式（34）代入式（33），可得

[y（s）=1（αs+1）nr（s）+[1-1（βs+1）m]d（s）.] （35）

由式（35）可知，二自由度內模控制器具有2個自由度，參數[α]、[β]分別可以對系統的目標值跟蹤特性和抗干擾特性與魯棒性進行獨立調節，解決了傳統內模控制需要在多個性能之間進行取舍的困擾。

根據第2章的內容可知，

[M（s）=1（Tds+1）（Tss+1）s/RTes2+s+1/Tm，Q2（s）=M（s）-1F2（s）， Q1（s）=F2（s）-1F1（s）.] （36）

其中[F1（s）、F2（s）]以式（32）和式（34）進行設計，為使系統可實現，兩者的階數m和n均取3。

4 仿真分析

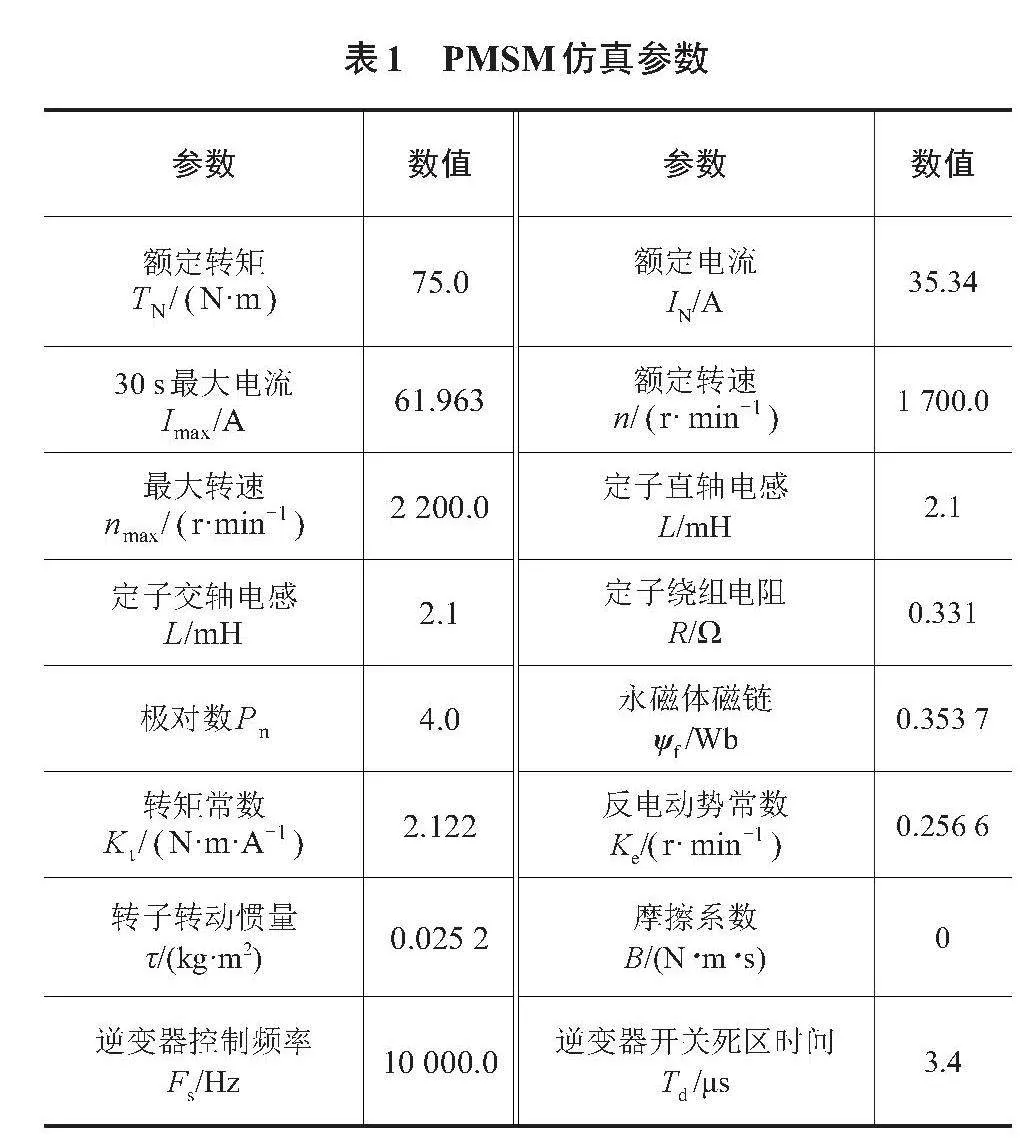
實驗所采用的PMSM參數如表1所示。

由表1中的數據和上文中的公式可以計算出該電機的電磁時間常數和機械時間常數分別為：[Tn=6.34 ms]，[Tm=2.78 ms]。由于機械時間常數小于電磁時間常數，所以此時的電機系統如果不對電流環的擾動項做處理，電流將會出現不可忽略的誤差。

根據表1中的數據在Matlab/Simulink中構建PMSM系統的雙閉環調速模型，采用轉子磁鏈定向的矢量控制并令[Id=0]。在此基礎上做了PI控制器（其中KcP= 1 460.36，KcI= 9.26，KsP= 3.06，KsI= 77.08，依據文獻（17）中的整定方法得出）與根據式（36）構建的二自由度內模控制器的對比試驗，其結果如下。

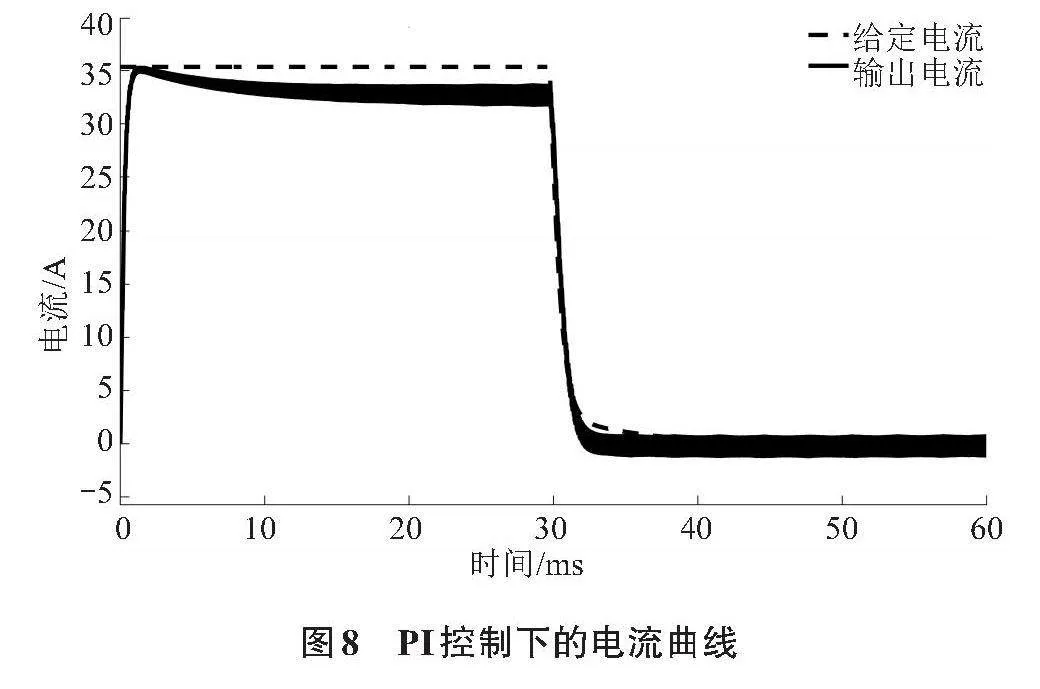
圖8為給定800 r/min的轉速時，采用PI控制得到的電流曲線。

由圖8可以看出在電機加速階段，輸出電流始終小于給定的輸入電流，兩者之間存在穩態誤差，這與式（17）所分析的結果一致，這種電流誤差的存在使得電機在加速階段始終不能以最大電流工作，進而使其在加速階段花費更長的時間。

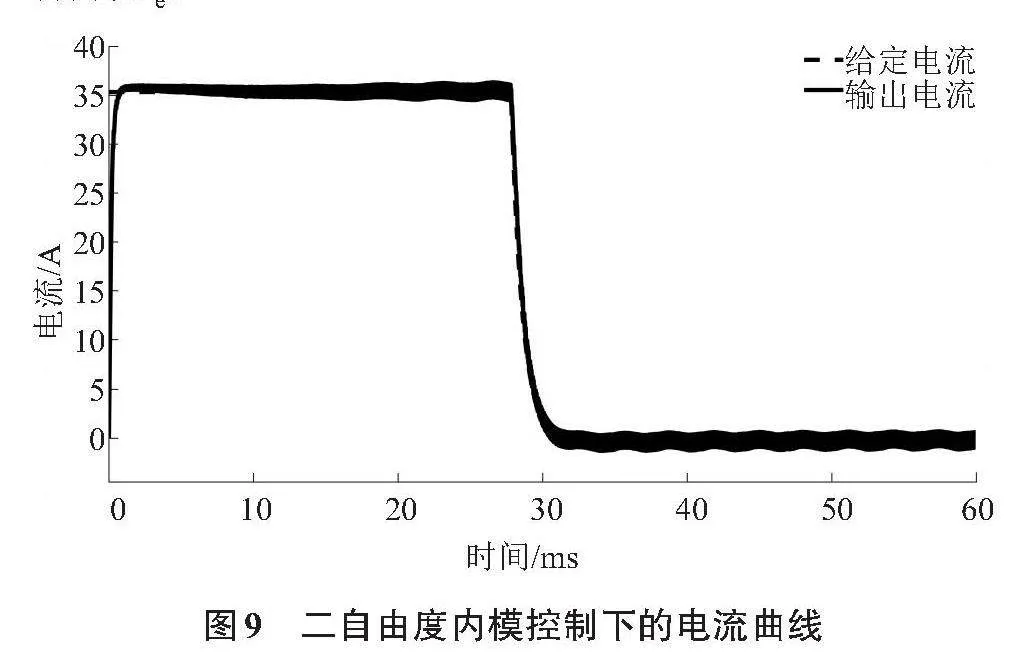
圖9為相同條件下，根據式（36）構建的內模控制器得到的電流曲線，其中參數[α=0.005Te]，[β=0.003Te]。

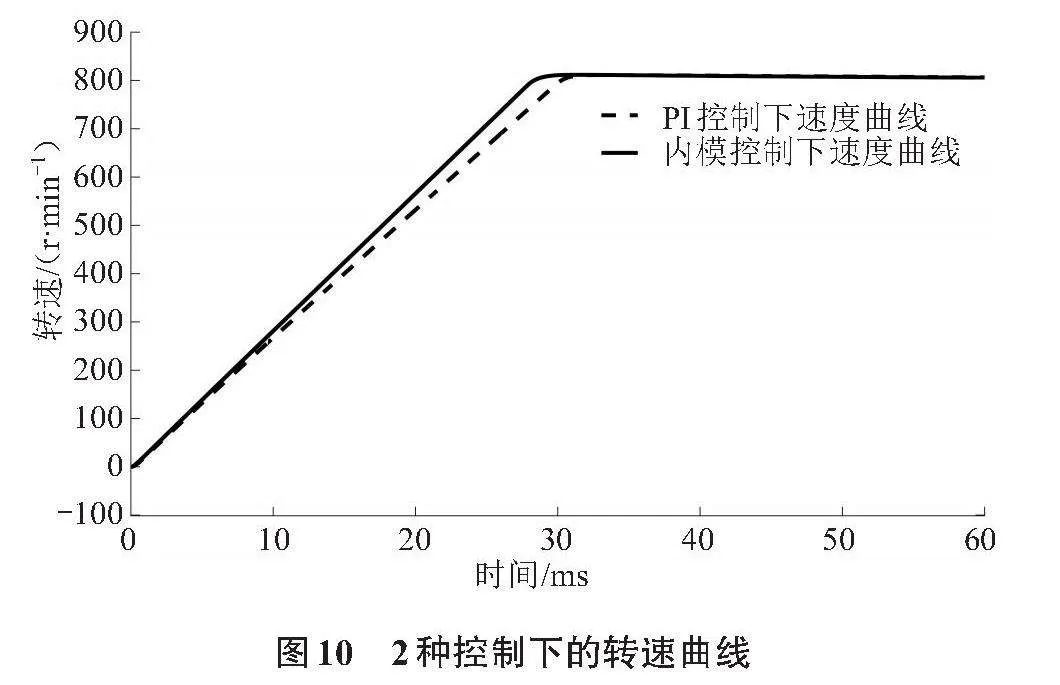
由圖9可以看出，在加速階段其輸出電流時刻依附于系統的給定電流，解決了PI控制中的問題。對比圖9和圖8可以看出，內模控制下的電流開始下降的時間約在27.61 ms，而PI控制約在29.68 ms，這說明內模控制下電機提前到達了給定轉速，其提速效果優于PI控制，具體情況如圖10所示。

因為內模控制解決了輸出電流與給定電流之間的誤差問題，其加速階段能夠以理想電流進行，所以在圖10中的加速段體現出了內模控制時刻大于PI控制的情況，且內模控制率先加速到給定轉速。

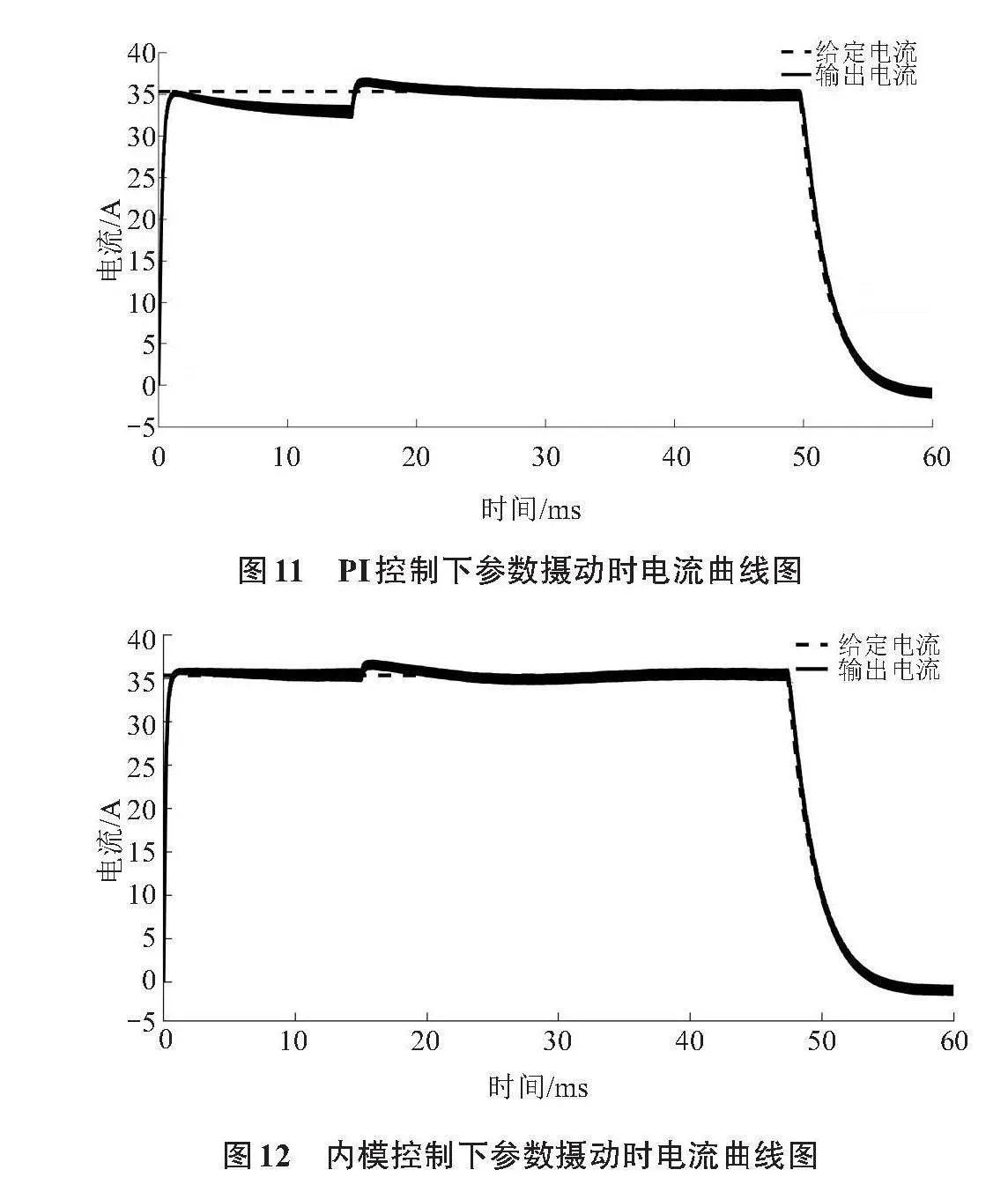
由于電機在運行的過程中有些參數會隨著工作環境的變化而發生攝動，為了測試所設計控制器和PI控制器的魯棒性，在與上文相同的實驗條件下，當電機運行至15 ms時將其轉子磁鏈衰減為原來的40%，得到結果見圖11、圖12。

將圖11與圖8對比、圖12與圖9對比，可知內模控制下的系統在參數發生攝動時，其電流波動和調節時間均小于PI控制，因此其魯棒性更優。

5 結論

本文建立了PMSM調速系統的數學模型，并對電流環使用PI控制的情況進行了分析。由式（14）和式（17）可知，當PMSM的機械時間常數小于或者接近于電磁時間常數時，如對反電動勢項忽略，則會使得電機的電流輸入與輸出之間存在一個明顯的穩態誤差，這將使得電機的動態性能變差。為解決此問題，本文設計了一種二自由度的內模控制器，由式（35）知其具有2個可獨立調節的參數，能分別調節系統的跟蹤特性和抗干擾特性，在理論上解決了PI控制的穩態誤差問題。最后在Matlab/Simulink上進行了所設計控制器與PI控制器的對比仿真實驗，由結果可知，所設計的控制器相比于PI控制器，其電流跟蹤特性更好，使得電機具有了更好的加速性能，同時其魯棒性也明顯優于PI控制，有助于小轉動慣量永磁同步電機在高性能場合下的應用。

參考文獻

[1] 陳卓易，屈穩太.基于PID型代價函數的永磁同步電機模型預測電流_{uWvR57UlGeKqrY4eoSRUSy5lWbr0ZtgwZKwvAEkvER0=}控制[J].電工技術學報，2021，36（14）：2971-2978.

[2] 王麗，高遠，袁海英.基于改進型SMO的PMSM無傳感器魯棒控制方法[J].廣西科技大學學報，2022，33（2）：48-53.

[3] MA X J，BI C.A technology for online parameter identification of permanent magnet synchronous motor[J].CES Transactions on Electrical Machines and Systems，2020，4（3）：237-242.

[4] 姚緒梁，黃乘齊，王景芳，等.兩相靜止坐標系下的永磁同步電動機模型預測功率控制[J].電工技術學報，2021，36（1）：60-67.

[5] 陳榮，鄧智泉，嚴仰光.永磁同步伺服系統電流環的設計[J].南京航空航天大學學報，2004，36（2）：220-225.

[6] 萬山明，吳芳，黃聲華.永磁同步電機的數字化電流控制環分析[J].華中科技大學學報（自然科學版），2007，35（5）：48-51.

[7] 洪帥，高遠，張銀，等.基于SRUKF的永磁同步電機無傳感器控制研究[J].廣西科技大學學報，2019，30（1）：46-51.

[8] 楊明，牛里，王宏佳，等.微小轉動慣量永磁同步電機電流環動態特性的研究[J].電機與控制學報，2009，13（6）：844-849.

[9] 徐建英，劉賀平.永磁同步電動機參考模型逆線性二次型最優電流控制調速系統[J].中國電機工程學報，2007，27（15）：21-27.

[10] MORIMOTO S，SANADA M，TAKEDA Y.Wide-speed operation of interior permanent-magnet synchronous motors with high-performance current regulator[J].IEEE Transactions on Industry Applications，1994，30（4）：920-926.

[11] 趙曜.內模控制發展綜述[J].信息與控制，2000，29（6）：526-531.

[12] LIU J，HUANG M Z，WANG Y.Research on vector-control system of PMSM based on internal model control of current loop[C]//2nd International Workshop on Computer Science and Engineering，Octorber 28-30，2009，Qingdao，China. IEEE，2009：297-301.

[13] HARNEFORS L，NEE H P.Model-based current control of AC machines using the internal model control method[J].IEEE Transactions on Industry Applications，1998，34（1）：133-141.

[14] 張井崗，李臨生.一種二自由度內模控制方法[J].工業儀表與自動化裝置，2002（4）：63-65.

[15] 解小剛，陳進.采用id=0的永磁同步電機矢量控制系統MATLAB/Simulink仿真[J].新型工業化，2016，6（5）：47-54.

[16] 袁雷，胡冰新，魏克銀，等.現代永磁同步電機控制原理及MATLAB仿真[M].北京：北京航空航天大學出版社，2016.

[17] 王光，王旭東，馬駿杰，等.一種快速SVPWM算法及其過調制策略研究[J].電力系統保護與控制，2019，47（3）：136-145.

[18] 賀明智，許建平，游小杰，等.環路延時對數字峰值電壓控制開關變換器瞬態性能的影響[J].中國電機工程學報，2009，29（6）：1-7.

[19] 王莉娜，朱鴻悅，楊宗軍.永磁同步電動機調速系統PI控制器參數整定方法[J].電工技術學報，2014，29（5）：104-117.

[20] 趙志誠，文新宇.內模控制及其應用[M].北京：電子工業出版社，2012.

[21] VANDEURSEN J M，PEPERSTRAETE J A.Internal model control with improved disturbance rejection[J].International Journal of Control，1995，62（4）：983-999.

[22] 杜文龍，陳俐，劉文通，等.考慮延遲的線控轉向二自由度內模控制[J].中國機械工程，2021，32（16）：1904-1911.

Two degrees of freedom internal model control of current loop of

permanent magnet synchronous motor

HUANG Bo， PAN Shenghui*， LIU Xingyu

（School of Automation， Guangxi University of Science and Technology， Liuzhou 545616， China）

Abstract： At present， when controlling permanent magnet synchronous motors（PMSM）in industry， it is often believed that the adjustment process of the current loop is much faster than the adjustment process of the speed loop， thereby the changes in the back electromotive force disturbance term in the current loop are neglected. However， for motors that use PI control and have a mechanicaLL9dleppRv20NSjhUbSjUObzhoKr+4uGduxM9jaG+EQ=l time constant that is not significantly different from the electromagnetic time constant or smaller， if the back electromotive force disturbance term in the current loop is directly ignored， it will lead to a significant deterioration in the dynamic response performance of the motor. To solve the above problems， this paper first established a mathematical model of the permanent magnet synchronous motor speed control system. Then， based on this mathematical model， the reasons for the dynamic performance deterioration of the motor under PI control conditions and the conditions that whether the back electromotive force disturbance term can be ignored were derived. In response to the situation that cannot be ignored， this paper designed a two degree of freedom internal model controller on the basis of traditional internal model control. This controller had two independently adjustable parameters that respectively adjusted the tracking characteristics， robustness characteristics， and anti-interference characteristics of the current loop. Finally， a comparative simulation experiment was conducted using Matlab/Simulink to compare the designed two degree of freedom internal model controller with traditional PI controller. The results show that the designed two degree of freedom internal model controller enables the current loop to have better tracking and robustness compared to the PI controller， solving the problem of poor dynamic response performance of the motor under special circumstances.

Keywords： permanent magnet synchronous motor（PMSM）; current loop; dynamic characteristics; internal model control; robustness

（責任編輯：黎 婭）

收稿日期：2023-09-11；修回日期：2023-11-27

基金項目：廣西自然科學基金項目（2018GXNSFAA138122）資助

第一作者：黃博，在讀碩士研究生

*通信作者：潘盛輝，副教授，研究生導師，研究方向：汽車電子控制技術、自動測試技術等，E-mail：gxustpsh@163.com