高中物理力學中動態平衡問題的求解技巧

摘要：動態平衡是指在調節特定的物理參數時，其他相關聯的物理參數也會相應發生變化.在這種變化過程中，盡管描述物體狀態的物理參數有輕微的波動，但在一段較短的時間尺度內，這些微小的變動可以被認為是處于一種平衡狀態.這類處于變化中的平衡狀態的問題被稱為動態平衡問題.通過具體案例，探討解決動態平衡問題的幾種不同方法，以幫助學生解決該類問題.

關鍵詞：高中物理；動態平衡；解題

中圖分類號：G632文獻標識碼：A文章編號：1008-0333（2024）28-0117-03

在力學的學習過程中，動態平衡問題作為其中一項重要內容，既充滿了挑戰性，又體現了物理學的實用性和深刻性.在實際教學中，動態平衡問題常常因為其復雜性而讓學生感到困惑.這些問題不僅涉及多種力的相互作用，還需要學生具備較強的分析能力和計算能力.而且，動態平衡問題中常常包括多個步驟的推理和運算，對學生的邏輯思維有較高的要求.因此，如何讓學生既能掌握動態平衡的基本原理，又能熟練地解決相關問題，是教師必須面對和解決的教學難題.

1解題步驟

（1）審題：仔細閱讀題目，理解題目中的物理現象和要求，此為解題的基礎.只有理解了題目，才能準確地找到解題的方向.

（2）畫圖：對于動態平衡問題，畫出物體受力的圖示是非常有用的.這可以幫助學生清楚地看到各個力的方向和大小，以便進行下一步的分析.

（3）建立物理模型：根據題目的描述，學生需要建立相應的物理模型，如相似三角形、矢量三角形等.這是解題的關鍵步驟，需要學生靈活運用已學的物理知識，掌握每個模型的適用條件.

（4）運用數學工具求解：建立好物理模型后，學生需要運用適當的數學工具對模型進行求解.這一步需要學生具備扎實的數學基礎.

2常用方法技巧

2.1矢量三角形法

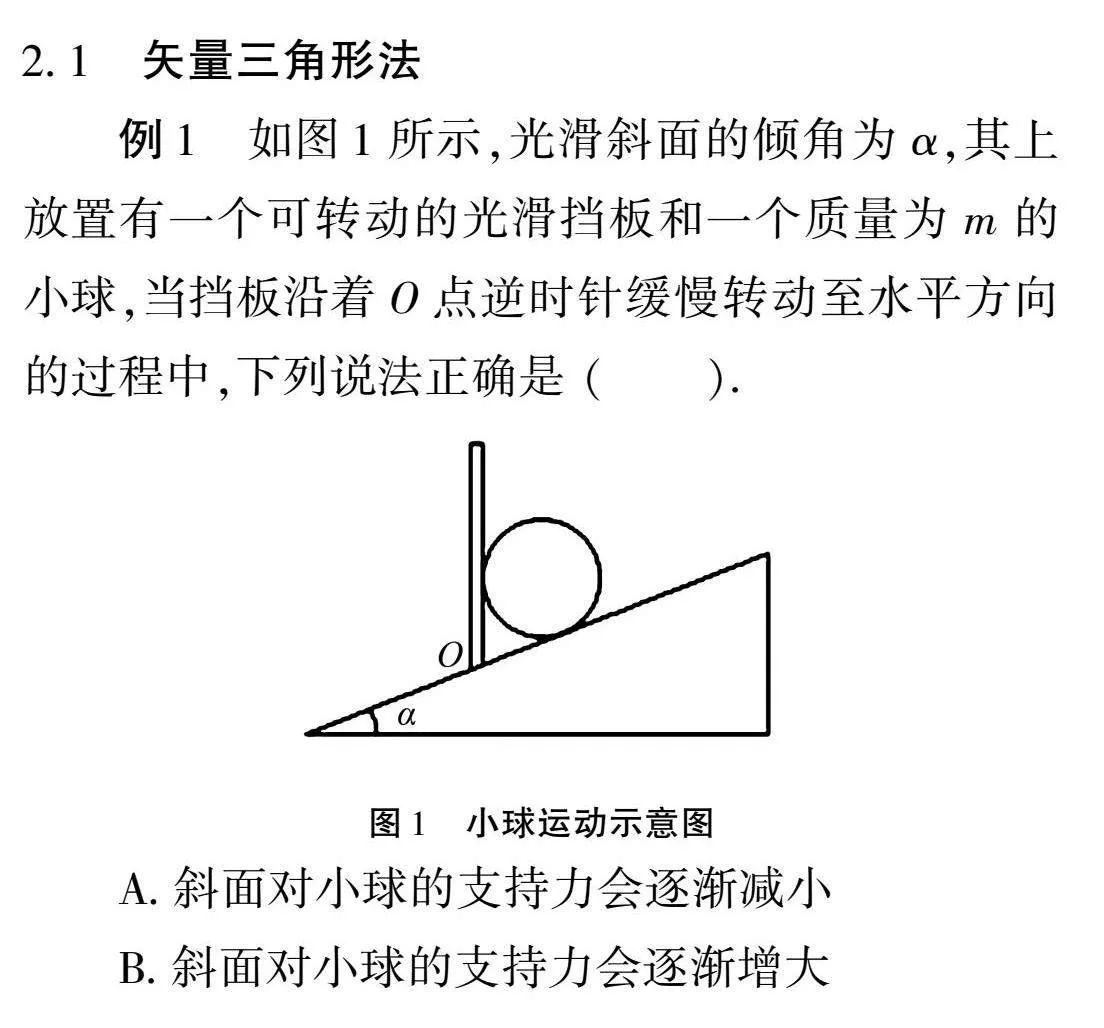
例1如圖1所示，光滑斜面的傾角為α，其上放置有一個可轉動的光滑擋板和一個質量為m的小球，當擋板沿著O點逆時針緩慢轉動至水平方向的過程中，下列說法正確是 （）.

A.斜面對小球的支持力會逐漸減小

B.斜面對小球的支持力會逐漸增大

C.擋板對小球的彈力先增大后減小

D.擋板對小球的彈力先減小后增大

解析選取小球為研究對象，對小球起始狀態進行受力分析，此時小球受到三個力，分別為重力mg、擋板對其施加的彈力FN2以及斜面對其施加的支持力FN1.當擋板沿著O點緩慢轉動時，重力mg大小和方向均不發生變化，支持力FN1的方向保持不變，一直垂直斜面，支持力FN1大小是未知量.彈力FN2的大小和方向此時均為未知量.三個力中，一個力大小方向已知，一個力方向已知，適合應用矢量三角形法[1].在緩慢移動過程中，小球所受到的合力為0.如圖2所示，根據平衡條件，此時支持力FN1和彈力FN2的合力跟重力mg大小相等、方向相反.分析不同位置時小球的受力，可以看出小球受到的斜面對其施加的支持力FN1會逐漸減小，其所受到的彈力FN2先減小后增大，當FN1和FN2垂直時，彈力FN2最小，故選項A、D正確.

2.2相似三角形法

例2如圖3所示，半圓環的最高點B處固定有一個定滑輪，該半圓環是由光滑的銅絲彎曲而成.某時刻，小明在圓環上掛一個質量為m的小球，且用細繩的一端將其拴住，然后將細繩的另一端跨過定滑輪，并在該端施加一個作用力F，在該力的作用下，小球自A點開始緩慢移動，則下列說法正確的是（ ）.

A.銅絲對小球的支持力FN的方向始終背離圓心O

B.銅絲對小球的支持力FN的方向始終指向圓心O

C.銅絲對小球的支持力FN逐漸變小

D.銅絲對小球的支持力FN大小不變圖3小球運動示意圖

解析首先對小球進行受力分析，起始處于A點位置時，小球在mg、FN和拉力FT的作用下處于平衡狀態.當小球緩慢移動時，此時重力大小方向保持不變，拉力和支持力的方向均發生變化.當物體受到三個力，且有兩個力的方向都未知時，此時可以運用三角形相似法[2].作出小球的受力分析圖，如圖4所示，由三角形相似有：mgBO=FNAO=FTAB，得FN=AOBOmg.根據圖中的幾何關系，線段AO、BO都不變，則銅絲對小球的支持力FN大小不變，方向始終背離圓心O，故A、D正確.

2.3正交分解法

例3如圖5所示，14圓弧槽固定在水平地面上，用推力F推動光滑小球由A點向B點緩慢移動，第一次推動過程中，力F的方向始終保持水平；第二次推動過程中，力F的方向始終沿圓弧的切線方向.則下列說法正確的是（）.

A.第一次推動過程中，推力F逐漸變大，圓弧槽對小球的支持力逐漸變小

B.第一次推動過程中，地面對圓弧槽的支持力不變，地面對圓弧槽的摩擦力不變

C.第二次推動過程中，推力F逐漸減小，圓弧槽對小球的支持力逐漸變小

D.第二次推動過程中，地面對圓弧槽的支持力逐漸變小，地面對圓弧槽的摩擦力先變大后變小

解析容易分析出小球的受力情況，選用正交分解法進行動態平衡分析[3].設小球與O點連線與豎直方向的夾角為θ，小球質量為m，圓弧槽質量為M，圓弧對小球的支持力為N，地面對圓弧槽的支持力為FN，地面對圓弧槽的摩擦力為f，則第一次推動過程中，對小球受力分析如圖6所示.

小球由A點向B點緩慢移動，可知小球受力平衡，將支持力N正交分解得F=Nsinθ和mg=Ncosθ.

小球從A緩慢移動至B點時，θ越來越大，則推力為F=mgtanθ，可知θ越來越大，推力越來越大；另外支持力為N=mgcosθ，可知θ越來越大，支持力越來越大，故A錯誤.對圓弧槽與小球整體分析，θ越來越大，豎直方向滿足FN=（M+m）g.可知，無論θ變化與否，地面對圓弧槽的支持力不變；另外由于整體受力平衡，水平方向滿足f=F.由于推力越來越大，所以地面對圓弧槽的摩擦力越來越大，故B錯誤.第二次推動過程中，對小球受力分析如圖7所示.

推力F始終與圓弧對小球的支持力N垂直，小球受力平衡，將重力mg正交分解得F=mgsinθ和N=mgcosθ.θ越來越大，則推力F越來越大，支持力N越來越小，故C錯誤.對圓弧槽與小球整體分析，θ越來越大，水平方向有f=Fcosθ=mgsinθcosθ=12mgsin2θ.

可知地面對圓弧槽的摩擦力先增大后減小；豎直方向由平衡關系式FN=（M+m）g-Fsinθ=（M+m）g-mgsin2θ.可知地面對圓弧槽的支持力逐漸變小，故D正確.圖7第二次推動過程中小球的受力分析示意圖

3結束語

動態平衡問題是高中物理力學中的重要內容，其求解過程對學生的物理思維能力有著極大的鍛煉價值.通過對動態平衡問題中常見的三種解題技巧的分析，可以發現每種解題技巧都有其對應的物理模型.矢量三角形法通過構建矢量的合成和分解，直觀地展示了力的平衡狀態，適用于多個力作用于同一點的情況.相似三角形法則通過利用幾何相似性來簡化復雜的力學關系，尤其在涉及平行力和比例關系的問題中非常有效.而正交分解法借助直角坐標系，將復雜的力分解為彼此獨立的分量，從而使問題的求解變得更加簡潔明了.在實際的求解過程中，學生要根據物理模型，靈活選取解題技巧，并在日常的學習過程中，不斷擴大自己的“技巧”庫.

參考文獻：［1］

楊軍林，楊彬.巧用矢量三角形分析力學問題[J].中學物理（高中版），2020，38（7）：58-60.

[2]姚鑫.妙用相似三角形法解決受力物體的動態平衡問題[J].數理化學習（高一二版），2013（5）：23-24.

[3]杜旭東.力學中涉及物體平衡的常考題型解析[J].數理化解題研究，2024（9）：85-87.

［責任編輯：李璟］