一道物理高考題引發的課堂啟示

摘要：學生解決問題的能動性是無限的.通過學生對一道物理高考題的“破解”過程，談如何在課堂中調動學生解決物理問題的能動性.

關鍵詞：高考題；破解；啟示；能動性

中圖分類號：G632文獻標識碼：A文章編號：1008-0333（2024）28-0102-03

教學是一門藝術，是一門內化于心、外化于行的藝術，既有“教”的藝術性，又有“導”的藝術性.老師引導得好，可以使課堂生成效果事倍功半.教學中給學生留有一定的時間和空間，讓他們獨立去思考、去討論、去生成新的知識.這樣既可以有效調動學生的學習積極性，又可以提升學生對知識的深層認知，使教與學產生共鳴，真正實現課堂教學的高效.本文就一道高考題講解過程

談一點自己的做法與反思.

1真題再現

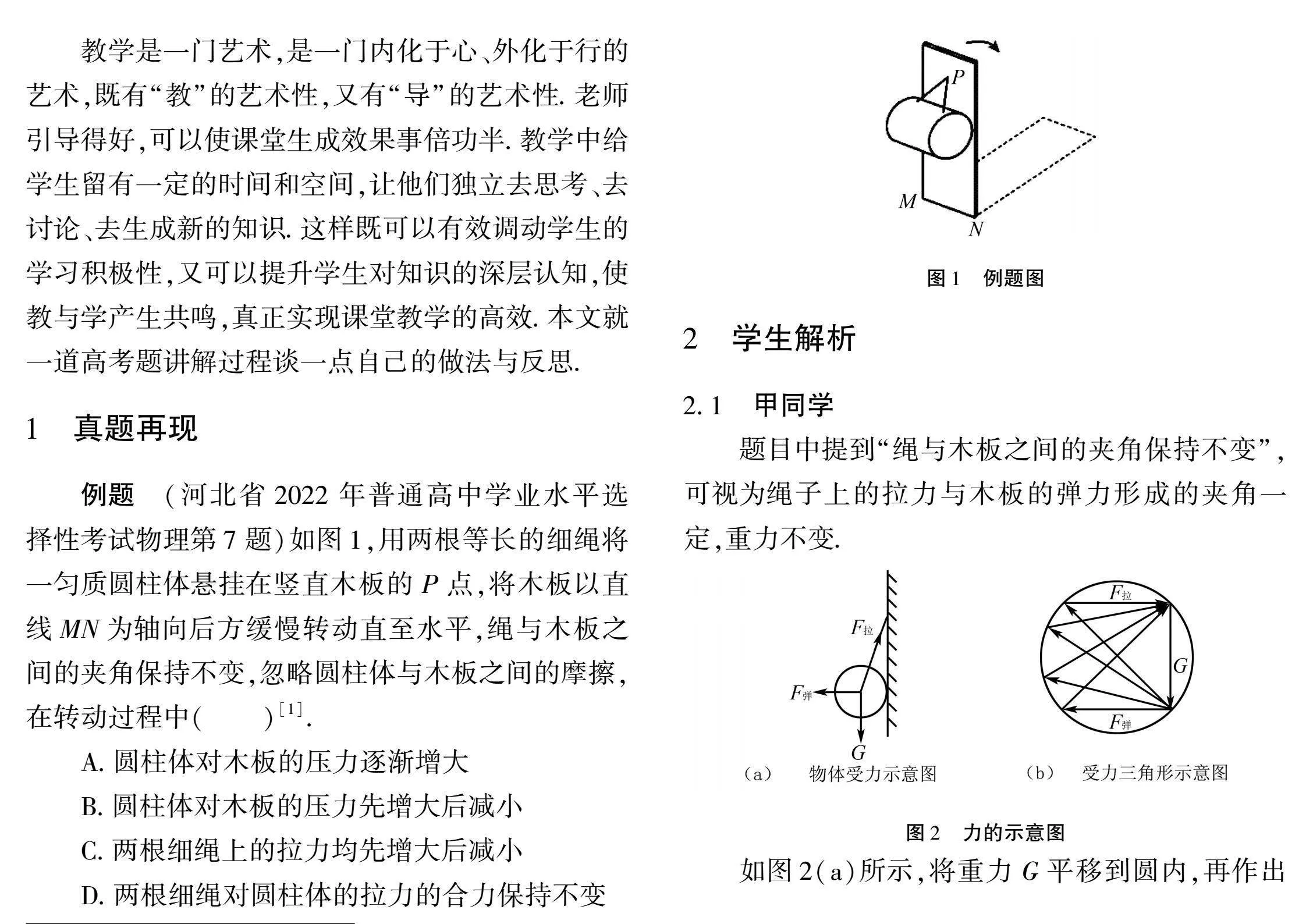
例題（河北省2022年普通高中學業水平選擇性考試物理第7題）如圖1，用兩根等長的細繩將一勻質圓柱體懸掛在豎直木板的P點，將木板以直線MN為軸向后方緩慢轉動直至水平，繩與木板之間的夾角保持不變，忽略圓柱體與木板之間的摩擦，在轉動過程中（）[1].

A.圓柱體對木板的壓力逐漸增大

B.圓柱體對木板的壓力先增大后減小

C.兩根細繩上的拉力均先增大后減小

D.兩根細繩對圓柱體的拉力的合力保持不變

2學生解析

2.1甲同學

題目中提到“繩與木板之間的夾角保持不變”，可視為繩子上的拉力與木板的彈力形成的夾角一定，重力不變.

如圖2（a）所示，將重力G平移到圓內，再作出彈力F彈和拉力F拉的矢量三角形，隨著角度變化，弦對應角不變，彈力F彈和拉力F拉的方向和大小發生變化，當彈力F彈過圓點時為圓上直徑，此時彈力F彈最大，再傾斜時彈力F彈又變小，如圖2（b）所示.則圓柱體對木板的壓力先增大后減小.故選B選項.

點評該生根據物體的受力分析以及題目信息，想到了運用力的三角形定則解決問題.相對而言，這種方法屬于物理當中解決物體在三個力的作用下處于動態平衡狀態問題的常規方法，但前提必須是其中一個力的大小和方向恒定，另外兩個力間的夾角恒定.

該生分析了三個力的特點，發現只有重力大小和方向不變，另外兩個力的大小和方向都可變，但兩個力間的夾角不變，然后將三角形定則進行了遷移運用，并分析出重力不是這三個力當中最大的力，即圖2（b）中重力G的示意圖不能畫在圓直徑處，最終通過圖解法表示了另兩個力的變化趨勢，表明該生對三角形定能夠準確、熟練地運用，達到了知識的內化程度.

2.2乙同學

由圖3可知：FN=mgcosθ+FTsinα

FTcosα=mgsinθ

聯立得：FT=mgsinθcosα

FN=mgcosθ+mgsinθtanα.

對FN中變量θ進行求導得：

FN′=mg（cosθ·tanα-sinθ）.

由于tanα>0，所以θ在0°～90°范圍內變化且大于某個角度β時，存在cosθtanα-sinθ大于零的地方，當小于這個角度時存在小于零的地方，即FN′在θ從0°～90°變化時先大于零后小于零，則FN在θ從0°～90°變化時先增后減，FN在θ從90°～0°變化時也是先增后減，如圖4所示（圖4只分析了tanα=1時的cosθ與sinθ的函數圖像，當tanα=k分析過程亦然）.則圓柱體對木板的壓力先增大后減小.故選B選項.

點評該生通過解析法，用恒力和三角函數寫出了變力FN的表達式，通過求解變力FN的導數，結合數學零點存在性定理，判斷出導函數FN′的值，進而判斷力FN的變化情況，充分運用了數學的相關知識，表明該生能夠將所學數學知識用來解決物理問題，做到了學科知識的融合，進一步提升了該生的數理結合能力.

2.3丙同學

由圖3可知：FN=mgcosθ+FTsinα

FTcosα=mgsinθ

聯立得：FT=mgsinθcosα.

代入上式得：FN=mgcosθ+mgsinθtanα

由于tanα是定值，

整理可得：FN=mg（cosθ+sinθtanα）.

由輔助角公式得：FN=mg1+tan2α（11+tan2αcosθ+tanα1+tan2αsinθ）

令sinφ=11+tan2α，cosφ=tanα1+tan2α

得到：FN=mg1+tan2αsin（θ+φ）.

因為mg1+tan2α為定值，

所以FN∝sin（θ+φ），

因為0°≤θ≤90°

所以φ≤θ+φ>90°+φ.

由圖5可知，由初狀態到末狀態sin（θ+φ）先增大后減小，故FN先增大后減小.則圓柱體對木板的壓力先增大后減小.故選B選項.

點評該生與乙同學一樣，用解析法寫出了變力FN的表達式，不同的是該生運用數學輔助角公式，通過定義域內函數極值問題得出了FN的變化趨勢，也表明了該生將數學知識用來解決物理問題的學科間知識融合應用的能力.

2.4丁同學

由圖3可知：FN=mgcosθ+FTsinα

FTcosα=mgsinθ

聯立得：FN=mgcosθ+mgsinθtanα.

對FN中變量θ進行求導得：FN′=mg（cosθ·tanα-sinθ）.

令FN′=0，則tanα=tanθ，此時θ=α，只有一個根.

當θ=0°時，FN′=tanα>0，則在0°≤θ<α時，FN′>0；在α<θ≤90°時，FN′<0，即FN′的圖像變化趨勢為圖6（a）所示，由FN′的圖像變化趨勢可知FN的圖像變化趨勢為圖6（b）所示.隨著θ減小，FN先增大再減小.則圓柱體對木板的壓力先增大后減小.故選B選項.

點評該生解題思想和方法與乙同學基本一致，可參照對乙同學的點評.

3教學反思

上面是我在上高三物理習題課時的一個片段.我深深地陷入思考，在課堂教學中如何調動學生處理和解決物理問題的能動性？本節課中我沒有因為一解而放棄多解，而是當同學們給出一種解題答案后追問：請同學們討論一下這道題還有其他解法嗎？同學們一個個爭先恐后地發表自己的見解，于是形成了上述至少四種解法.由此反思，我們是否更多地將固有的傳統的課堂模式轉變成以更加注重調動學生解決物理問題能動性的誘因，來實現物理課堂教學的高效？善誘則通，善思則得.怎么樣把老師“誘”的頻率調到學生在課堂中“思”的波段上，以便讓老師的“主導驅動力”和學生“主體內在驅動力”產生共鳴，達到“老師的教”與“學生的學”統一和諧？值得我們每一位身處一線教學的老師去思考、反思.

新課程理念下的課堂教學過程是一個師生互動、交流和思維碰撞的過程，正是這個過程，學生在課堂中提出了很多超出老師課前預設的問題.因此，課堂教學中教師應及時捕捉師生思維碰撞產生的有探究價值的新問題，同時以情境為契機，調整原本的課堂教學，推進現有課堂教學的生成和發展，從而使課堂異彩紛呈[2].同時，老師要積極鼓勵學生敢于質疑，培養學生敢于質疑的課堂意識.這就需要老師在平時的教學中、與學生的相處中要具有民主作風，有意識地創造一些討論性活動，學生間、師生間就能出現思維的激情碰撞，迸發出智慧的火花.

4結束語

什么樣的課堂才是高效、合理的課堂？我認為適合學生的、充滿個性張揚的課堂才是高效合理的課堂.一切為了學生，學生在教師的引導下能獨立自主地、自由開放地學習，在課堂學習過程中學會感悟、體味生活，在與知識的“碰撞”中，引導學生釋放自己的能動性，使知識插上翅膀引領學生飛翔.只有當學生樂學、善學、肯學時，課堂才能成為學生的樂園學堂，這樣的課堂才是真正高效合理的課堂.

參考文獻：［1］

朱啟明，王瑤，李康麗.例析圖解法在多力多體問題中的應用[J].物理通報，2023（06）：85-88.

[2]程笑宇.出乎預設之外 生成意外之果：例談課程資源的動態生成[J].中學物理教學參考，2012，41（06）：67-69.

［責任編輯：李璟］