用函數解決實際問題考查抽象能力

立德樹人是教育的根本任務．大部分學生將來不以數學為職業．數學教育在這些學生的生活及職業發展中的作用，主要體現在運用數學解決實際問題．這是學生“有本領”的主要體現．課標對學生綜合運用所學知識解決問題能力的考查，給出了具體要求．課標指出，要在情境中考查核心素養，注重考查學生的應用意識與創新意識[1]．中考命題要貫徹課標的要求，注重考查運用知識解決問題的能力．函數是初中解決實際問題的主要工具．用函數解決實際問題的試題，注重考查思維過程，是改變相對固定的試題形式，減少“機械刷題”的抓手．

1 當前函數試題的現狀與困境

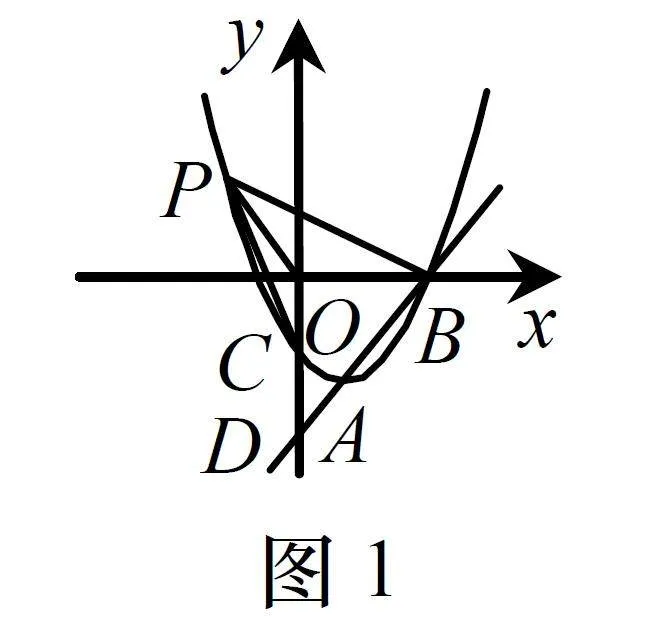
函數題一度作為壓軸題．為了保證區分度，試題形式不斷變化．有一段時間認為，綜合運用知識就是在知識交匯處命題．中考曾經出現了一些函數與幾何交匯的試題．當時被認為是創新．典型的題目如下：

如圖1，已知直線y=kx?6與拋物線y=ax2+bx+c交于A，B兩點，且點A（1，-4）為拋物線的頂點，點B在x軸上．

（1）拋物線的第二象限圖象上是否存在一點P，使ΔPOB與ΔPOC全等？若存在，求出點P的坐標；若不存在，請說明理由；

（2）若點Q是y軸上一點，且ΔABQ為直角三角形，求點Q的坐標．

該題中的拋物線是二次函數圖象．問題是找出滿足條件的全等三角形和直角三角形．解答題目需要算邊長（長度，即兩點間距離，兩點間距離公式為高中解析幾何內容）、角度，做輔助線，構造全等與相似．長度與角度是幾何問題，不是函數問題．函數是研究變量間的關系，通過這種相依數量關系來研究變化規律．做輔助線，構造全等與相似是典型的平面幾何方法．該題的實質是以函數圖象為背景，考查平面幾何．數學是自然的，有其產生的背景與脈絡，在歷史發展中形成了研究問題與方法．人為的隨意交匯，不能產生有意義、有價值的問題．

兩點間距離公式為高中解析幾何內容．該題卻不是經典的解析幾何問題．解析幾何產生于十七世紀的歐洲，是在社會需求下產生的．當時，機械研究提出了動力學相關的數學問題，堤壩修建提出了力學相關的數學問題，航海業提出了測量問題，造船業提出了描繪船體各部位曲線問題，望遠鏡的制造提出了透鏡表面形狀問題，火器制造業提出了拋射體軌跡與定量計算問題，這些問題推動了解析幾何的產生．高中解析幾何運用坐標法，主要探討曲線的方程，曲線的交點及其延伸出的兩點間距離，直線的斜率及其代表的角度，核心概念是距離和斜率，主要方法是列方程與解方程（組）．這些研究問題、內容與方法，是自然形成的，不能與函數或者平面幾何知識隨意交匯而產生有意義、有價值的問題．人為的知識交匯，只能創造“牛頭馬面”式的虛構問題．

函數試題的另一種創新形式是含參數的函數問題，這主要是向高考銜接，本質上是多元函數問題．含參的一次函數題，大部分表現為線性規劃問題．教育部《關于做好2022年中考命題工作的通知》明確要求，嚴格依據課標命題，不得擴大考試內容范圍，嚴禁將高中課程內容作為考試內容．這兩類題擴大了考試內容范圍，違背了以大概念（大概念是數學家對數學內容的概括與總結，教育功能是遷移）[2]為核心、以結構化知識為載體的課標要求．

學業質量標準要求，以結構化數學知識為載體考查核心素養，在情境中考查核心素養[1]．按照這個要求，把關題的載體是多樣的，函數題不應必然作為壓軸題．中考應該是多點把關、知識輪動，才能做到試題形式多樣化，從而使學生減少刷題．

2 函數試題要著重在現實背景中0eeb621311badcef871990eedbe58d4af1d90124145367252a36fed785328b3c考查抽象能力

函數產生于實際問題中，它是描述現實問題的基本數學工具．初中學的函數比較簡單，單純在數學內部考查函數知識，沒有很好的區分度．函數在實際問題中的應用，有較好的區分度，體現了數學的價值——運用數學解決現實中的問題．這是堅持素養立意，堅持試題內容與育人目標相結合的一種命題思路．

2.1 對實際問題中函數關系的理解是考查抽象能力的一個切入點

實際問題多是用自然語言描述的．若實際問題中的數量較多，則多用圖象或圖表表達．圖象與圖表是一種視覺表征，是視覺推理的一種應用．讀懂圖象與圖表是理解實際問題的關鍵，也是一種重要的數學素養．圖象整體表達數量（函數）關系，直觀揭示變化規律．理解圖象表達的現實意義及函數關系，是抽象能力的一個重要表現；也是考查抽象能力的一個切入點．下題就是一個典型樣例．

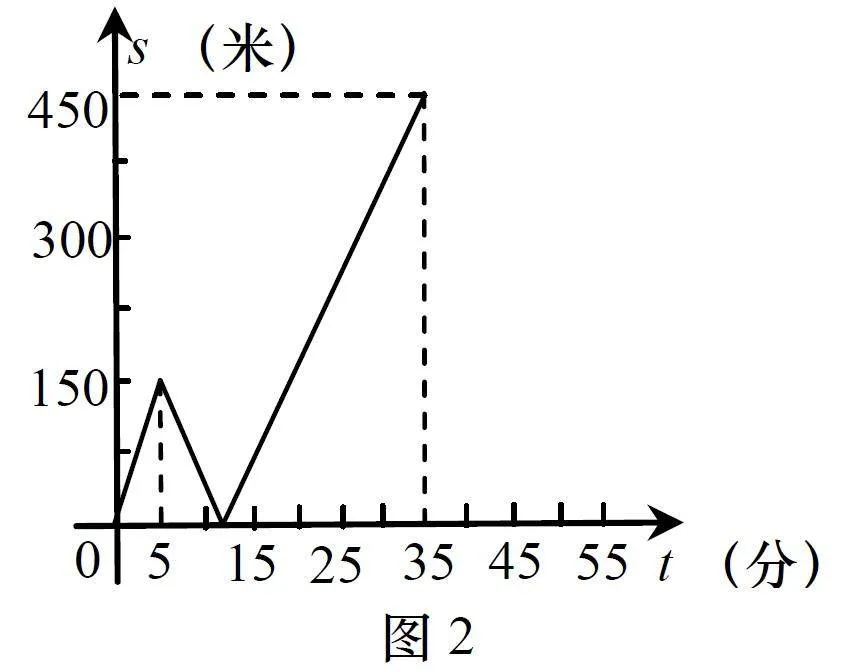
甲乙兩人勻速從同一地點到1500米處的圖書館看書，甲出發5分鐘后，乙以一定速度沿同一路線行走．設甲乙兩人相距s（米），甲行走的時間為t（分），s為t的函數．圖象一部分如圖2所示．當甲出發多少分鐘時，甲、乙兩人相距360米[3]？

該題典型地體現了數學的閱讀方式——先整體把握問題，生成一種假設，再通過閱讀尋求證據驗證假設[4]．該題的縱坐標，不是學生熟悉的路程，而是路程差．這給學生理解問題帶來困擾．對圖2的解釋，學生需要調用學校生活經驗．甲步行先走（乙未動），兩人間的距離拉大．乙5分鐘后以大于甲的速度（如騎自行車）追趕．從橫軸5分鐘時刻起，兩人間距開始減少．乙趕上甲時，兩人間距變成零．之后間距再次拉大，直到乙到達圖書館．此時間距最大．乙到達圖書館后停止移動，甲繼續向圖書館移動，兩人間距又開始減少，直至變成零．從圖象看，兩人間距曾達到450米，說明最大間距不小于450米．題目所求間距360米的時刻，應該有兩個（最大間距對應時刻前后各一個）．圖象只是部分運動過程，不是全部．

調用學生的生活經驗來讀懂圖象是學生理解該題的關鍵，這是視覺推理的一種重要表現，是數學眼光的重要成分．該題可以用函數知識來做．利用函數與方程的關系，也可以用方程來做．這類題聚焦函數和方程的核心思想，考查抽象能力，有多種解法，有一定的區分度．函數應用是教材的重點內容．教材中有很多用圖象表達的素材（也有縱軸是路程差或者進水量與出水量差的素材）．在這種素材上編制有區分度的試題，真正體現了回歸教材，以標命題，把中考內容與育人目標相結合．

運用圖象進行大小比較是用函數知識解決問題的一類典型問題．大小是一種重要的數量關系，也是生活中的一類重要問題，是函數增減性（單調性）的重要應用，如效用最大，花費最少等問題．初中、高中教材中也有很多這類問題．依據這些素材編制一些拓展性題目，也是一種回歸教材的命題思路，既考查了應用意識，也考查學生進一步學習的知識準備情況，典型體現了中考的目的．

2.2 識別核心變量及其關系是考查抽象能力的著力點

有些問題數量關系較多．學生往往抓不住核心變量．能從實際情境中抽象出核心變量，是數學抽象能力的主要表現[1]．依托數量關系多的素材，命制函數應用題，是考查抽象能力的一個著力點．

人教社教材中有一個租車問題：

某學校計劃在總費用2300元的限額內，租用汽車送234名學生和6名教師集體外出活動，每輛汽車上至少要有1名教師．現在甲、乙兩種大客車，甲種客車最大載客量45人，乙種客車最大載客量30人．甲種客車每輛租金400元，乙種客車每輛租金280元．請給出最節省費用的租車方案[5]．

該題數量多，數量關系多．數量關系是典型的“總價=單價×數量”與“總量=分量+分量”，核心變量是總費用與甲、乙兩種客車費用．甲、乙客車的載客人數是次要因素．識別核心變量是構建該題思路的關鍵．學生對該題大多沒有思路，教師也認為不好講．這是一個有區分度的題，可以利用簡化條件法進行改編[6]，命制中考題．

把載客人數的要求去掉，固定車輛總數，仍然體現主要思路．可變為簡單問題：甲種客車每輛租金400元，乙種客車每輛租金280元，在總費用2300元的限額內，若租7輛客車，給出最節省費用的租車方案．

該題拓展一下，可以變為較難題：甲種客車每輛租金400元，乙f4b359f69370270f346ab616363febbca3be1462e0381d9a2f1500683227c7a3種客車每輛租金280元；甲種客車最大載客量45人，乙種客車最大載客量30人．在總費用2300元的限額內，租用汽車送234名學生與8名教師集體外出參加活動，每輛汽車上至少有1名教師，給出最節省費用的租車方案．

教材例題控制條件，使得只能有6輛車．較難題與例題思路一致，車輛總數可以取幾個值，變成幾個最小值之間的比較，復雜度增加．簡單題與拓展題組成一個大題，簡單題大部分學生會做，也啟發拓展題思路，體現層次性，是一種有價值的命題思路．

在命制含有多個數量關系的題目時，需要仔細斟酌數量及數量關系，確保實現命題意圖．教材有這樣一道習題：A城有肥料200噸，B城有肥料300噸．現要把這些肥料運往CD，兩鄉．從A城運往CD，兩鄉肥料的費用分別為20元每噸與25元每噸，從B城運往CD，兩鄉肥料的費用分別為15元每噸與24元每噸．現C鄉需要肥料240噸，D鄉需要肥料260噸，怎樣調運運費最少[4]？

本題可以用一次函數的增減性來做，也可以利用直覺推理來做．B城運往CD，兩鄉的運費，分別比A城運往CD，兩鄉的運費低．優先把B城中的肥料運往CD，兩鄉．B城運往C鄉的運費最低，優先運往C鄉．C鄉需求240噸肥料，B城有300噸．B城運240噸肥料往C鄉，剩余60噸只能運往D鄉．A城所有的200噸肥料，也只好運往D鄉，恰好滿足條件．假如B城運往C鄉的肥料中，有1噸被A城肥料替換．B城被A城替代的1噸需要運往D鄉，則總運費增加（2015）（2415）14?+?=元，所以上述調運方案最優．這種直覺推理，本質上還是利用一次函數的增減性，最值在定義域端點處取得．學生沒有意識到一次函數的本質作用，也可以單純依靠直覺推理得到結論．該題命題意圖如果是考查一次函數，則需要改進．比如把數據調整一下（該題數據調整充滿陷阱，只有滿足一個較為特殊的條件才行）．該題命題意圖如果是考查數學核心素養，則是一道好題．它的背景簡單，學生都能理解．它有多種解法，既可以用直覺推理來做，也可以用一次函數來做．它蘊含了重要的數學知識與能力，如函數和邏輯推理．它可以進一步展開與一般化，變成線性規劃問題，其函數解法也可以一般化．

實際問題的情境是多樣的，即使費用最少這類問題，其背景也是多樣的．可以結合地域特色來命制，凸顯育人導向．實際情境可以多個維度復雜化，像結合視覺推理，用圖象與表格表達數據；或者增加一些起次要作用的數量關系限制主要變量的取值范圍等，從而拓展命制不同難度的題目．

參考文獻

[1]中華人民共和國教育部．義務教育數學課程標準（2022版）[S]．北京：北京師范大學出版社，2022

[2]格蘭特·維金斯，杰伊·麥克泰格．追求理解的教學設計（第二版）[M]．上海：華東師范大學出版社，2018

[3]呂銀愛，董濤．基于數學運算素養的解題分析與教學建議[J]．福建基礎教育研究，2019（11）：61-63，89

[4]舒爾曼．實踐智慧[M]．上海：華東師范大學出版社，2014

[5]人民教育出版社．義務教育教科書·數學（八下）[M]．北京：人民教育出版社，2013

[6]吳玲玲，董濤．運用簡化條件法教解題——以2017年全國Ⅰ卷理21題為例[J]．福建中學數學，2021（1）：31-33

（本文系福建省教育科學規劃2022教育考試招生重點專項課題“基于初中學業水平考試評價體系的考試內容改革實施路徑研究”（課題編號：FJJYKS22-22）的研究成果）