需求變動視角下虛擬養老服務人員調度研究

摘要： 針對虛擬養老服務人員實時調度問題，基于需求變動視角分別構建成本最優的調度優化模型和擾動最小的干擾管理模型，通過改進灰狼優化算法的位置更新公式，引入非支配排序設計多目標遺傳灰狼優化算法。通過求解標準算例對比算法求解指標驗證了算法的優越性，通過設計并求解算例驗證模型的可行性。研究結果表明：相較于重調度法，干擾管理模型能夠顯著降低干擾事件對各主體的影響，生成更為豐富的決策集合，更加適合虛擬養老服務人員的調度問題。

關鍵詞： 虛擬養老；調度問題；干擾管理；前景理論；遺傳灰狼優化算法

中圖分類號： N945；C934文獻標識碼： A

Research on Virtual Elderly Care Service Personnel Scheduling from the Perspective of Demand Change

LIAO Yang，MENG Haonan，LI Yingfeng，Li Siqing3

（1.School of Management， Xi’an University of Architecture and Technology， Xi’an 710055， China; 2.Research Center of Green Development and Mechanism Innovation of Real Estate Industry in Shaanxi Province， Xi’an 710055， China; 3.School of Economics and Management，Xi’an Shiyou University，Xi’an 710065， China）

Abstract：In order to solve the real-time scheduling problem of virtual eldly service personnel， this paper constructs a cost-optimal scheduling optimization model and a disturbance-minimization management model based on the perspective of demand variation， by improving the location update formula of grey wolf optimization algorithm， the non-dominated ranking design multi-objective genetic grey wolf optimization algorithm is introduced. The superiority of the algorithm is verified by solving the comparison index of the standard example， and the feasibility of the model is verified by designing and solving the example. The results show that， compared with the rescheduling method， the disturbance management model can significantly reduce the influence of disturbance events on the agents， generate more abundant decision sets， and is more suitable for the scheduling problem of virtual elderly service personnel.

Keywords： virtual pension; scheduling problem; interference management; prospect theory; genetic-grey wolf optimization algorithm

0 引言

近年來，虛擬養老院在多個城市落地成為老年人養老選擇的新方式。虛擬養老是由服務者搭建服務平臺，通過信息化平臺捕捉老人的需求并安排服務人員為老人上門服務。相較于傳統的養老模式，虛擬養老能夠讓老年人足不出戶享受專業化服務，同時其智能化監測設備也能對老年人身體狀況進行實時監測，以確保發生緊急狀況時及時做出響應，使之不再局限于傳統居家養老的被動式服務。

服務運營過程中，如何滿足老人需求的同時提高資源利用，合理制定服務人員的調度方案是每個虛擬養老服務商必須考慮的問題。盡管人員調度問題擁有較為豐富的研究成果，但虛擬養老院的服務模式、服務內容以及服務對象的特殊性對虛擬養老服務的調度問題提出了更高的要求。養老服務人員調度問題從屬于護工調度問題［1］，傳統的路徑優化問題是在各項信息已確定的基礎上制定調度方案，屬于確定性優化決策，然而在本問題中，老人需求常常伴有不確定性，需求變動時有發生，這就導致調度問題不能僅從靜態視角下展開確定性的決策優化調度。如何針對服務過程可能發生的干擾事件，例如：服務變動、時間窗變更以及老人發生緊急狀況等做出響應并及時調整調度方案，降低干擾事件對于各參與方造成的不利影響具有重要意義。在當前研究中，Euchi［2］以成本最小為優化目標，采用混合蟻群算法求解家庭醫護人員的路徑選擇問題。Taboumand等［3］則是在前者的基礎上將服務人員的資質條件納入約束，并采用分支定價算法對問題進行求解。Decerle等［4］考慮優化成本的同時將服務人員的路徑平衡也作為優化目標，并采用Memetic算法對模型進行求解。Haddadene等［5］則是提出了服務人員的偏好值，并以最小化成本和最大服務偏好為優化目標，構建多目標優化模型。袁彪等［6］研究了家庭護理中的醫療服務人員調度問題，考慮了隨機的客戶服務時間和最遲開始服務時間約束并建立了帶補償的隨機規劃模型。楊欣潼等［7］綜合考慮了老人服務時間窗戶和護工專業技能水平建立居家養老護工調度和路徑規劃問題模型。任宗偉等［8］分別從老年人等待時間、老年人對護理人員偏好和老年人對服務價格偏好構建老年人感知滿意度函數；以最大化老年人綜合感知滿意度和最小化社區居家養老服務中心運營成本混合整數非線性規劃數學模型。丁峰等［9］是針對多中心社區居家養老服務調度問題，以最小化總運營時間為目標，建立帶機會約束的隨機規劃模型。Shi等［10］考慮到了服務事件的隨機性，將客戶需求視為一個模糊變量，并以成本最小化為優化目標。Yuan等［11］考慮到了服務變動以及服務時間窗變動，通過度量老人、服務人員和公司擾動偏差，以偏差加權和最小化構建數學模型并采用禁忌搜索算法進行求解。Cappanern等［12］針對居家養老調度問題中服務取消和對新增額外需求等情況提出了非標準基數約束的求解方法。Bazirha等［13］則是考慮了老人服務延誤對調度問題的影響，針對考慮了服務中可能發生的意外事件將最小化延遲懲罰成本加入目標優化。綜合來看，當前服務調度問題擁有較為豐富的研究成果，學者也通過增加約束來滿足實際，但同時使得優化模型更為復雜。就研究視角來看，當前的研究主要是在靜態視角下展開的，僅有很少的文獻考慮實時調度問題。當需求變動發生時，如何最優的調整調度方案是亟待解決的問題。基于以上討論，本文的研究是基于需求變動視角對服務人員的實時調度展開研究。當前，針對本文研究問題的類型，學者主要采用重調度和干擾管理。重調度是通過全局優化重新制定方案，是一種動態的方法來處理干擾事件［14］。然而如果采用全局優化通常會對初始的調度方案造成較大改動。由于虛擬養老院自身的服務屬性，加之其是由多主體共同參與，大幅度的調整調度方案勢必會對各主體產生較大影響。因此，如何調整方案并考慮各參與主體的利益才是本問題研究的關鍵。干擾管理是針對實際問題和干擾事件建立相應模型，利用有效的算法進行求解［15］。相較于重調度，干擾管理是以降低干擾的不利影響為優化目標，盡可能降低擾動影響，對于本文的研究具有學術參考。同時，干擾管理思想也被廣泛應用于物流配送［16］、車間調度［17］、航空［18］以及城市公共交通［19］等多個領域。因此本文在虛擬養老服務運營的背景下，綜合考慮老人需求變動的干擾事件，構建調度模型，研究結果能夠為虛擬養老服務商調度安排提供決策依據。

1 模型構建

1.1 問題描述

本文研究的問題可描述為：在初始調度方案執行中，T時刻發生干擾事件致使初始調度方案難以繼續執行，此時需要對調度方案進行調整。為確保研究的推進，本文設置以下條件并將其轉化為模型的約束條件：1）服務開始時，每位服務人員從服務中心出發完成各自任務后回到服務中心；2）每位老人只能由一位服務人員服務；3）每位老人都有自己的服務時間窗，服務人員須在老人的服務時間窗內進行；4）虛擬養老院必須針對老人的需要安排服務人員。

1.2 變量說明

n：老人的數量；m：服務人員的數量；n1：干擾事件發生后已完成服務的老人數量；n2：干擾事件發生后未完成服務的老人數量；V={V V2，…，Vm，Vm+ Vm+2…，Vn}：老人集合；V1={V V2，V3，…，Vn1}：干擾事件發生后已完成服務的老人集合；V2={Vn1+ Vn1+2…，Vn2}：干擾事件發生后未完成服務的老人集合；K={k k2…，km}：服務人員集合；V0：虛擬養老服務中心；μ1：干擾對老人的擾動；μ2：干擾對虛擬養老服務商的擾動；μ3：干擾對服務人員的擾動；C：表示調度方案總成本；Cf：表示調度方案的固定成本；Ck：表示單位距離成本；TD：表示當前調度方案的總距離；［ei，li］：老人i的服務左右時間窗；wki：服務人員k到老人i的時間；ri：老人i需要的服務需求；dki：服務人員k自身所能提供的服務類型；tij：服務人員k從i到j的路程時間；si：老人i的服務時間；xkij：表示服務人員k由老人i處前往j處；yki：表示老人i由服務人員k完成服務。

1.3 確定性優化決策：初始調度模型

本文首先從確定性優化決策調度展開研究，首先要在一直服務需求、服務時間窗等條件下，即老人需求不發生變動的理想情況下，以成本最優構建初始調度模型：

minC=Cf+Ck·TD（1）

∑i，j∈Vxk0j= k∈K（2）

∑j∈Vxkj0= k∈K（3）

∑i，j∈Vxkij-∑i，j∈Vxkji=0，k∈K（4）

ei≤wki≤li，i∈V，k∈K（5）

ri=dki，i∈V，k∈K（6）

wki+si+tij-wkj≤（1-xkij）M，i∈V，k∈K（7）

∑i∈V∑j∈Vxkij≤|S1|- S1V，k∈K（8）

∑i∈V∑j∈Vxkij= k∈K（9）

∑k∈Kyki= i∈Vv（10）

xkij={0，1}，yki={0，1}，i，j∈V，k∈K（11）

其中，式（1）為初始調度方案模型的目標函數，C為調度方案的總成本，其中包括服務人員的固定成本和受路程距離影響的可變成本；式（2），（3），（4）表示服務人員從服務中心出發完成各自任務后返回服務中心；式（5）和為時間窗約束要求服務必須在老人要求的服務時間窗內進行；式（6）為服務約束，表示該服務人員必須能夠提供老人所需求的服務；式（7）是用于確保服務的連續性，其中M為一個大的正值；式（8）用于消除自回路，其中S1為服務人員的訪問路徑員；式（9）和式（10）表示每位老人只被訪問一次，并只接受一位服務人員的服務，以確保每個需求點被服務；式（11）為01約束。

1.4 擾動度量

在初始調度方案執行過程中，由于干擾事件的發生例如服務內容變動，時間窗改變等情況，此時就需要虛擬養老服務商針對干擾事件對前文求解的調度方案進行局部優化，降低干擾事件的不利影響。如果度量干擾事件對各主體造成的擾動大小成為首先需要解決的問題。前景理論是Tversky和Kahneman提出的，通常被用于不確定狀況下的優化決策［19］。前景理論的價值函數通過設置參考點來判斷收益或損失，能夠反應主體對客觀事實的主觀感知。由于現實中行為人是非完全理性的，發生干擾事件后通過度量受影響的個體對于損失的主觀感知能夠更加把握行為人的內心，能夠更加符合問題實際。因此基于前景理論，對各個目標的值函數進行表示，其中目標i的價值函數μi（x）如式（12）所示：

μi（xi）=xαii，xi≥0-λi（-xi）βi，xi<0（12）

其中，αi，βi，λi分別表示收益風險系數、損失風險系數和損失厭惡系數。αi、βi（0<αi<1，0<βi<1）分別表示收益和損失情況下的風險偏好程度，λi（λi>1）用來衡量人們對風險的規避程度，越大表示決策者對損失越敏感。前景理論指出，當面對收益時，由于收益風險的存在，隨著收益的增加人們會表現出風險規避；在面對損失時，隨著損失的增加，人們表現出風險追求。其中參考點表示收益或損失為0。本文通過參考前景理論的價值函數可以計算出干擾事件對于各參與主體的擾動大小。

1.4.1 干擾事件對老人的擾動度量

干擾事件對對老人的直接影響是接受服務時間發生變更，原定時間可能會產生偏差。由于老人需求的服務具有異質性，不同服務內容對于時間要求并不相同，例如生活照料、家政服務等生活化服務相較于醫療服務、緊急救助等具有較為寬松的調整時間，基于以上考慮，本文針對老人不同的服務內容建立擾動度量函數。對于服務時間較為寬松的家政服務、起居照料、情感陪護等生活服務，放寬對老人接受服務時間的要求，但盡可能應當在老人的時間窗內進行，否則即視為造成不利影響，其擾動度量函數如式（13）所示。對于醫療服務這類時間要求較為嚴格的服務，其擾動度量函數如式（14）所示。因此干擾事件對所有老人的擾動度量μ1如式（15）所示：

μ11（ti）=-（t′i-ti）α t′i<ei0，ei≤t′i≤liλ1（ti-t′i）β t′i>li（13）

μ21（ti）=-（t′i-ti）α ti≤t′iλ1（ti-t′i）β ti>t′i（14）

μ1=μ11+μ21（15）

其中，ti為新方案中老人i接受服務的開始時間，t′i為初始方案中老人i接受服務的時間，ei和li分別為老人i的左右時間窗。

1.4.2 干擾事件對虛擬養老服務商的擾動度量

干擾事件發生后，虛擬養老服務商會由于干擾事件被迫調整原有的調度方案造成成本的增加，因此相較于原方案，成本的增加最小是虛擬養老服務商所追求的目標。由故本文選擇初始調度方案的總成本為參考點，建立擾動度量函數：

μ2（C）=0，C≤C′λ2（C-C′）β2，C>C′（16）

其中，C為調整后方案的總成本，C′為初始方案的總成本。

1.4.3 干擾事件對服務人員的擾動度量

調度方案的調整通常會造成服務人員的工作量變動，造成工作時間延長或縮短，因此最少的加班工作時間是服務人員所追求的目標。故本文選擇初始調度方案中每個服務人員k的工作時間為參考點，建立擾動度量函數：

μ3（Tk）=-（T′k-Tk）α3，Tk≤T′kλ3（Tk-T′k）β3，Tk>T′k（17）

其中，Tk為初始調度方案中服務人員k工作的總時長，T′k為調整后方案中服務人員工作的總時間，其中工作時間包括服務時間和路程時間。

1.5 不確定性優化調度：干擾管理調度模型

實際調度過程中往往會由于干擾事件而難以執行，因此本節以1.4節中的擾動度量最小化為優化目標，針對不同干擾事件在滿足各項需求的條件下對初始調度方案進行調整，建立干擾管理調度模型：

min（∑i∈V2μ1（ti）/n2）（18）

min（μ2（C））（19）

min（∑k∈Kμ3（T）/m）（20）

∑i，j∈V2xkij= k∈K（21）

∑j∈V2xkj0= k∈K（22）

∑i，j∈V2xkij-∑i，j∈V2xkji=0，k∈K（23）

ei≤wki≤li，i∈V2，k∈K（24）

ri=dki，i∈V2，k∈K（25）

wki+si+tij-wkj≤（1-xkij）M，i∈V2，k∈K（26）

∑i∈V2∑j∈V2xkij≤|S2|- S2V2，k∈K（27）

∑i∈V2∑j∈V2xkij= k∈K（28）

∑k∈Kyki= i∈V2（29）

xkij={0，1}，yki={0，1}，i，j∈V2，k∈K（30）

其中，式（18），（19），（20）為干擾管理調度模型的目標函數，分別表示干擾事件對老人、虛擬養老院服務商和服務人員的擾動最小；式（21），（22），（23）表示當干擾事件發生后，服務人員從當前位置出發完成各自任務后返回初始的服務中心。式（24）為時間窗約束要求服務必須在老人要求的服務時間窗內進行；式（25）為服務約束，新的調度方案中服務人員必須能夠提供老人所需求的服務；式（23）是用于確保服務的連續性，其中M為一個大的正值；式（27）用于消除子回路，其中S2為服務人員的訪問路徑；式（28），（29）表示每位老人只被訪問一次，并只接受一位服務人員的服務，以確保每個需求點被服務；式（30）為01約束。

2 算法設計與研究步驟

針對前文的兩個調度模型，本章針對兩個調度模型的特點設計了優化算法。針對1.3節單目標優化的初始調度模型，本文設計了遺傳灰狼優化算法；1.5節的多目標優化的干擾管理調度模型，本文在前者算法的基礎上設計了多目標遺傳灰狼優化算法。具體步驟如下述。

2.1 初始調度方案求解

2.1.1 編碼與解碼

由于本文求解的是離散化的服務人員調度問題，為了更加直觀描述，采用整數編碼的方式，能夠簡化編碼和解碼方式，因此本文選擇以老人的編號進行編碼排列，舉例如圖1所示。其中，10 102，201為虛擬養老服務中心，數字的第1位數是該服務人員所能夠提供的服務類型，第3位數為該服務人員的編號，上例中如201，表示服務類型為2，編號為1的服務人員從服務中心出發，依次服務完3號和8號的老人最后回到服務中心，這種做法能夠確保算法能夠在解碼階段區分不同服務類型的服務人員，以判斷是否發生供需不匹配的情況。

2.1.2 貪婪算法構建初始解集

初始解的質量會直接影響算法的求解效率，避免大量無效解的產生同時縮小無意義的搜索空間。為了提高初始解的質量，本文采用貪婪算法來構建初始解集。本文研究中，路程距離和服務時間窗約束同時會對結果產生較大影響，因此本文參考文獻［21］，通過求解各節點的時空距離來構建初始解，時空距離公式：

DSTij=a1DSij+a2DTij，a1+a2=1（31）

其中，DSTij為老人i和老人j之間的時空距離，DSij為兩點之間對的空間距離，本文中取節點i與節點j之間的直線距離，DTij為兩點之間的時間距離，a a2為權重參數。當兩個節點時空距離越近，表明從一點到達另一點的“可行性”越大。假設老人i和j的服務時間窗為［ei，li］和［ej，lj］，我們令ei<ej，則服務人員在為老人i到達老人j的時間wkj∈［ei+si+tij，li+si+tij］，記e′j=ei+si+tij，l′j=li+si+tij。則老人i與老人j的時間距離為

DTij=ej-l′j，l′j<ejwkj-wki，ej≤e′j<lj，e′j<ej<l′jSymboleB@，e′j>lj（32）

2.1.3 離散化灰狼優化算法位置更新

在傳統灰狼優化算法中，狼群是依靠頭狼來引導位置完成連續尋優，位置更新公式可參照文獻［22］。由于本文屬于離散化尋優問題，故不適用傳統灰狼優化算法的位置更新公式，因此采用遺傳算法中的交叉算子來實現狼群的位置更新，我們要求狼群以一定概率隨機向頭狼α，β和δ靠近，位置更新公式：

Xi（t+1）=cross（Xit，Xα（t）），rand≤13cross（Xit，Xβ（t）），13<rand<23cross（Xit，Xδ（t）），rand≥23（33）

其中，Xα（t）、Xβ（t）、Xδ（t）為α、β、δ狼的個體，Xit和Xi（t+1）為灰狼i更新前后的個體。本文采用部分匹配交叉（PMX）來實現狼群更新，狼群隨機選擇頭狼靠近的同時，拓寬了算法的搜索空間，一定程度上解決了算法的“早熟”問題。

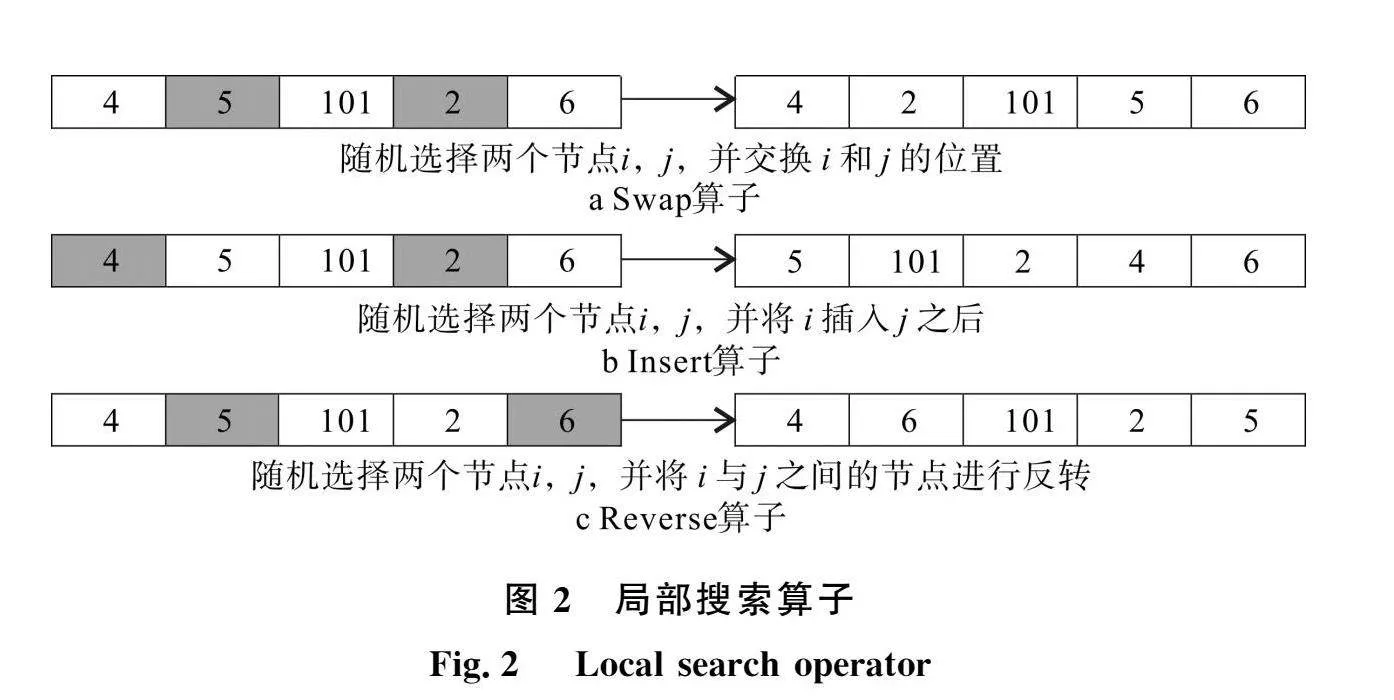
2.1.4 鄰域搜索算子

本文采用3種局部搜索算子（Swap，Insert，Reverse）來提高算法的局部搜索能力，圖2是對這3種搜索算子的介紹。

2.2 干擾管理模型求解

本節在前者算法的基礎上建立了多目標遺傳灰狼優化算法用于求解多目標優化問題，主要是針對該算法的初始化和多目標優化處理。

2.2.1 初始化

干擾管理的思想是以擾動最小為目標對初始調度方案進行局部調整以滿足問題要求。針對研究問題，本文設計了如下的初始化準則。假設T時刻發生干擾事件并使得初始調度方案不可行，此時需要明確T時刻已完成服務和未完成服務的老人集合，同時在編碼中剔除已完成服務的老人編號。假設初始調度方案為：0→1→4→5→0，0→2→6→7→0，0→3→8→0，當T=150時，7號老人的需求發生變更，此時老人 4，2，3已完成服務，則需要對剩下未完成服務的老人進行編碼求解，編碼方式如圖3所示。

2.2.2 多目標離散灰狼優化算法

對于多目標優化問題，在求解過程中，其各個優化目標往往會產生沖突。不同于單目標優化問題求解的單一最優解，多目標優化問題的最優解是由多個Pareto最優解，又稱非劣解構成的Pareto最優解集。當前針對多目標優化問題的處理方法主要包括：加權法、字典序法以及計算該問題的Pareto前沿。由于加權法難以合理確定各個優化目標的權重系數，而字典序法不能為決策者提供不同目標函數的權衡分析，而Pareto前沿可以得到多個非支配的最優解，在本文的研究中，能夠為虛擬養老服務商提供豐富的決策空間。因此在前文介紹的離散化灰狼優化算法中加入非支配排序，計算出Pareto最優解集。

3 仿真實驗

3.1 算法性能比較

3.1.1 單目標算法性能對比

良好的算法性能意味著更高的求解效率，更優的求解結果和良好的收斂效果。在初始調度求解中，本文建立了以成本最優為目標的調度模型，并設計了遺傳灰狼算法。為了進一步驗證算法的性能，本文從車輛路徑問題的solomon標準算例［23］并中選取6個標準算例并添加老人的服務需求、單位成本、固定成本等以滿足本文條件約束。本文在windows10操作系統，內存為8G，處理器為英特爾Core i76700HQ的計算機上采用Matlab R2016a進行編程，將本文的遺傳灰狼算法和傳統的遺傳算法實驗20次得到結果對比如表1所示。

可以看出，在初始調度方案求解中，本文構建的遺傳灰狼算法的求解效率和結果較傳統的標準遺傳算法求解具有顯著優勢。

3.1.2 干擾管理調度算法性能對比

針對不確定優調度優化，本文在遺傳灰狼優化算法的基礎上建立了多目標離散灰狼優化算法用于求解干擾管理調度模型。由于多目標優化問題求解過程中其各個目標往往會產生矛盾導致難以衡量解的優劣，通過求解該問題的非支配解構成的Pareto最優解集來達到目標。為了進一步驗證本文算法的性能，采用本文算法和NSGA-II算法，從以上6個算例中選擇人數規模不同、分布范圍不同的3個算例，通過設置干擾事件并進行求解，并選擇Spacing指標和C-Metric指標用于衡量算法的性能，其中Spacing指標能夠表示解集分布的均勻性，值越小則解分布越均勻，C-Metric為占優性指標，計算的是解集S2中的解至少被S1中的一個解支配的比例，C（A，B）越大則代表解集A的質量較解集B的質量越好。

從以上兩個算法的性能指標來看，本文建立的多目標離散灰狼優化算法優于NSGA-II算法。Spacing指標表明本文的優化算法求得的最優解集的分布更加均勻，C-Metric指標表明本文算法的非劣解較NSGA-II算法更加占優。

3.2 算例求解

本文通過問卷調查以及電話訪談的方式對虛擬養老院的服務模式和服務內容進行了解。服務以社區為依托，針對老人的服務需求派出具有相關技能資質的服務人員提供上門服務，同時為老人安裝監測系統對老人進行實時監測，以應對老人突發疾病、摔倒等情況。在二維平面內，有一處虛擬養老服務中心位于（50，50），能夠提供包括家政服務、起居照料、情感陪護和醫療服務在內的4種服務，共有30個老人遍布在區域內，以上四種類型的服務人員單位固定成本分別為：100，150，200和300元，單位距離成本為1元。

3.2.1 初始調度方案求解

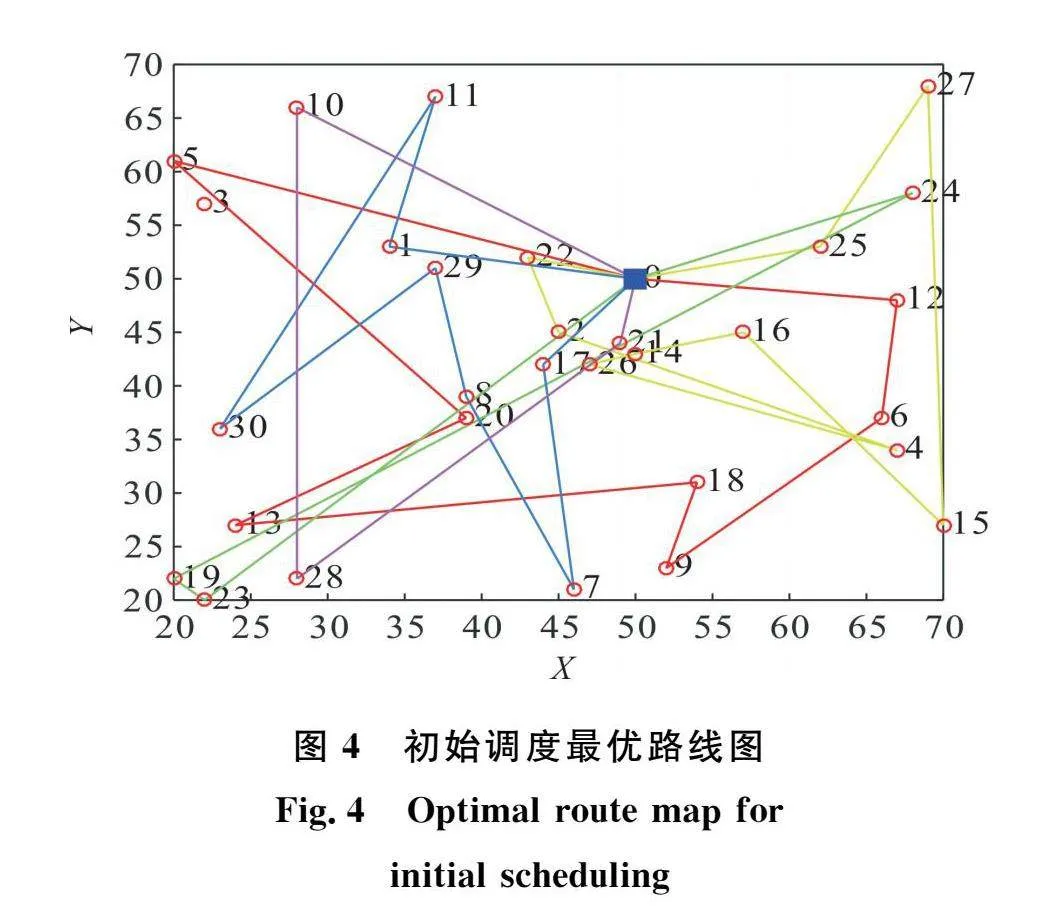
初始調度方案求解中，為了平衡時間窗和距離的比例，令a1=0.5，a2=0.5，設置灰狼種群為200，最大迭代次數為300，并設置最大鄰域搜索次數為20次，求得初始調度結果和最優路線圖如表3和圖4所示。

3.2.2 干擾管理模型求解

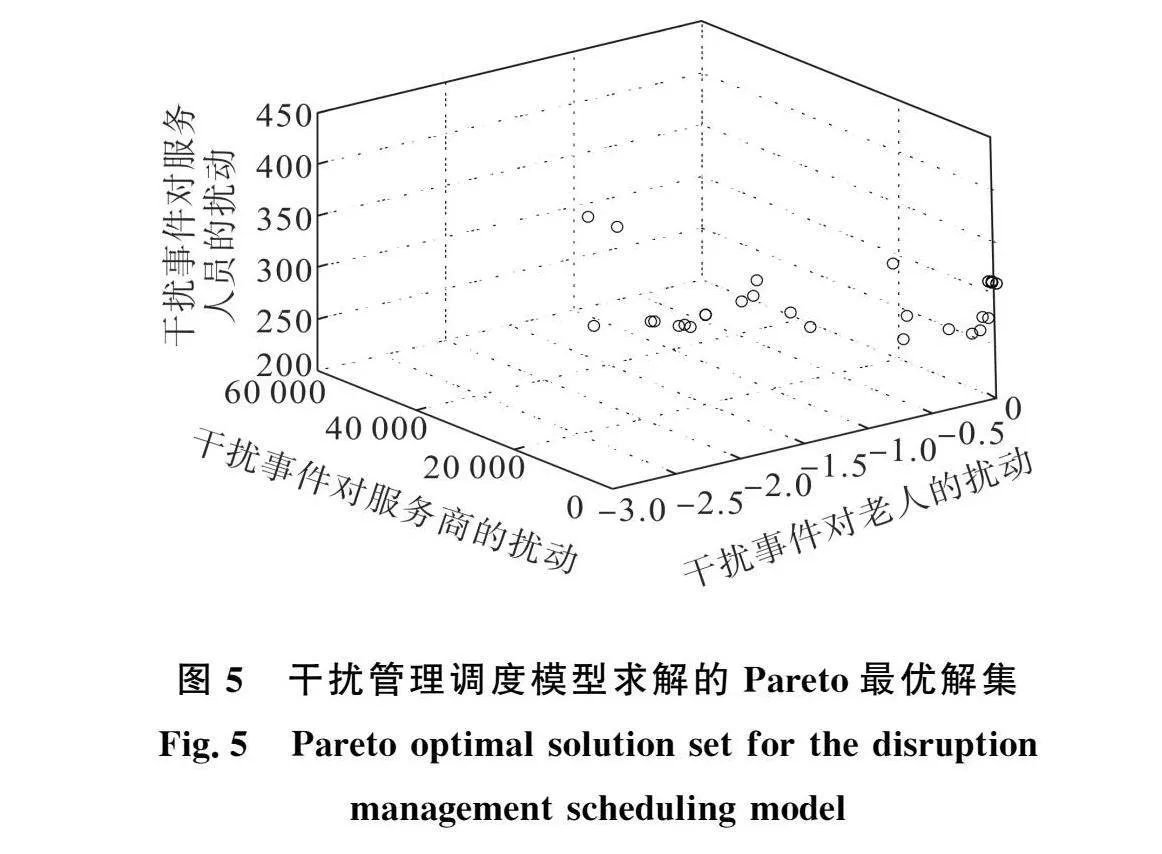
在不確定調度優化過程中，本文設置以下的干擾事件用于模擬現實中的干擾情境：1）T=200時，12號老人的服務時間窗從［650，723］變更為［342，405］，即服務提前；23號老人的服務時間窗從［640，735］變更為［350，420］，服務提前；2）T=240時，老人11發生緊急狀況，需要醫療護理人員立刻前往；3）T=300時，新增31號老人，位置為（35，50），其服務時間窗為［32 380］，需要感情陪護的服務人員，同時老人30取消服務。參考文獻［19］，本文令λ1=λ2=λ3=2.25，α1=β1=β2=β3=0.88，采用多目標灰狼優化算法對本文構建的干擾管理模型進行求解，得到Pareto最優解集如圖5所示。

本文從求得的Pareto最優解集中選擇成本最優的調度路線用于展示，調度方案和路線圖如表4所示。

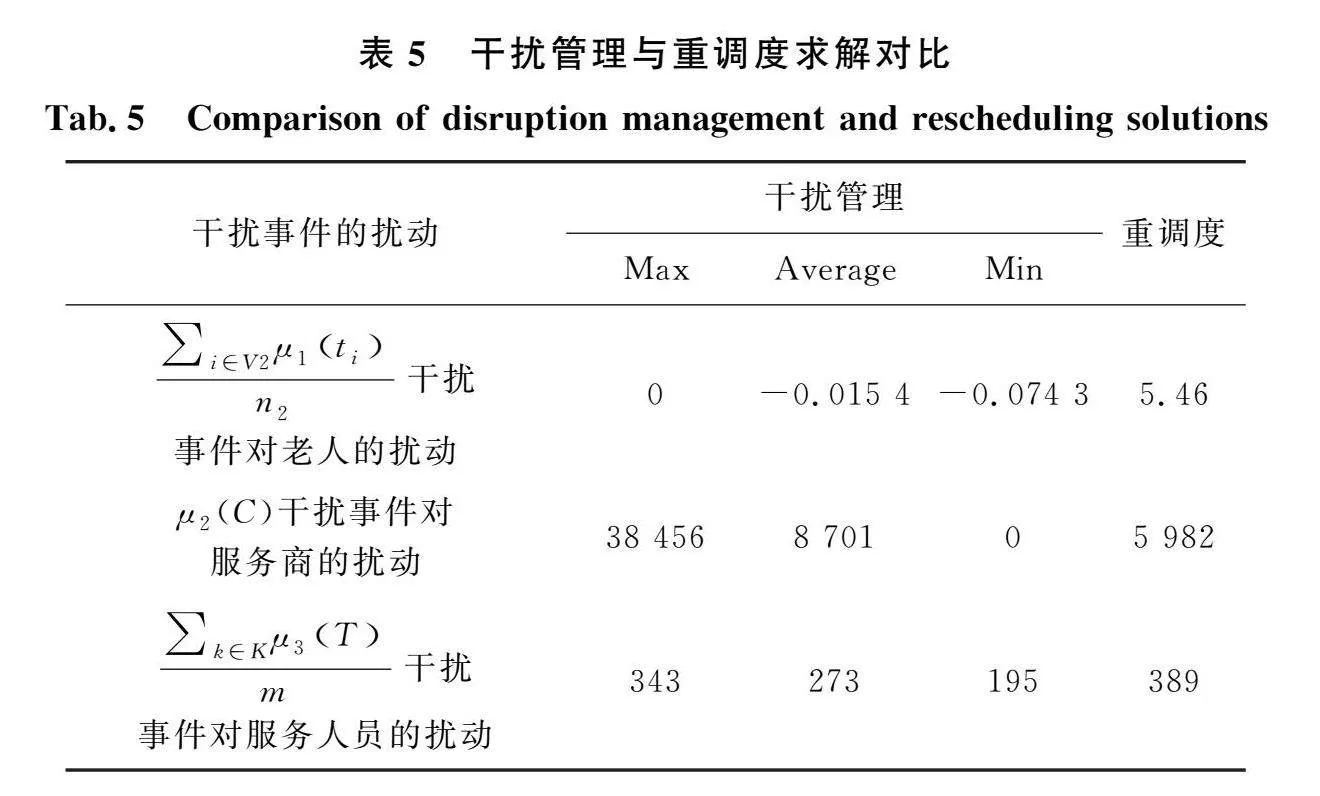
為了驗干擾管理調度模型的性能，本文同時采用重調度法在仿真環境和干擾情境相同的條件下對本文的算例進行求解，結果作為本文參考。重調度法是以成本最優為優化目標，對調度方案進行全局調整以滿足各項約束，不同方法的求解結果如表5所示。

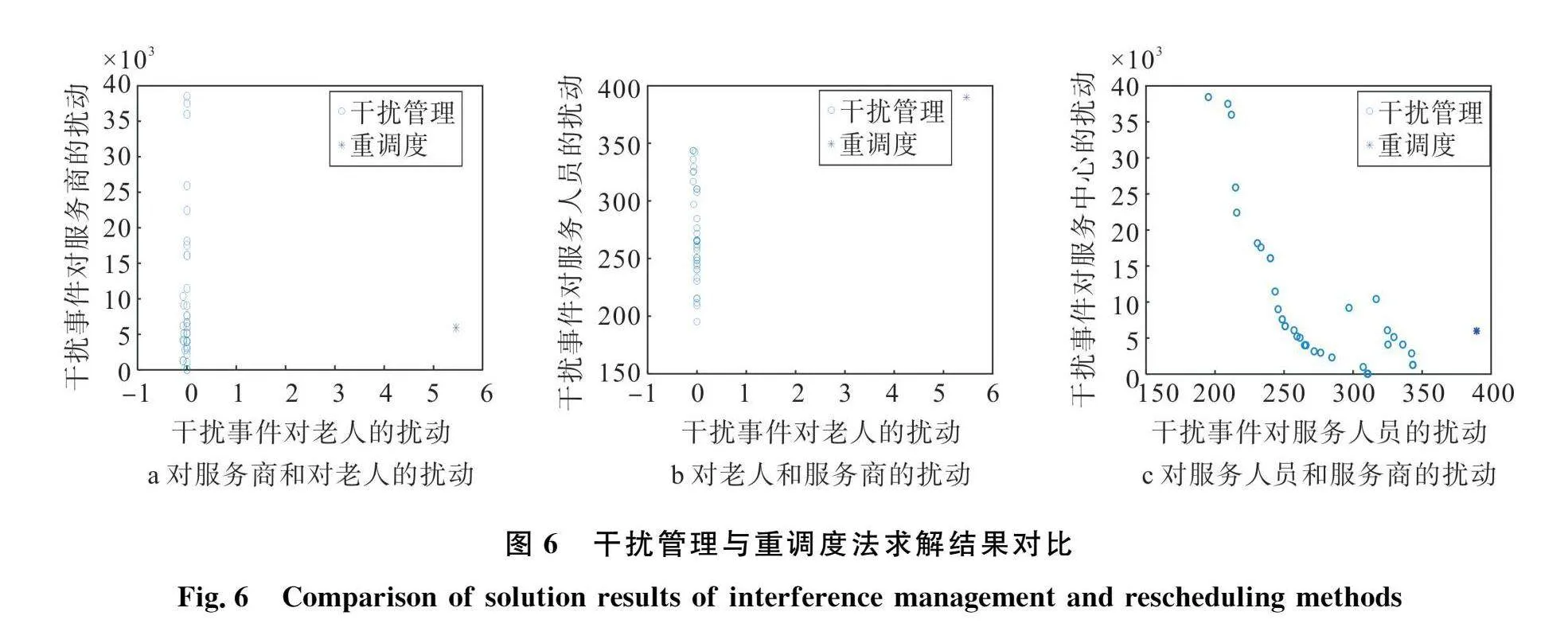
總體來看，本文構建的干擾管理調度模型具有更好的求解效果，為了更加直觀的對比兩種方法的結果，本文繪制出兩種方法的求解結果對比圖像如圖6所示。

從圖6能夠看出，相較于重調度法，本文的干擾管理調度模型能夠顯著降低干擾事件對老人和服務人員的擾動，在成本控制的方面也表現出了良好的效果。綜合來看，本文的干擾管理模型在本問題中能夠面對各種干擾事件時及時對初始方案進行調整，生成對各方影響較小的調度方案。長遠來看，虛擬養老院是自身的服務屬性，在服務人員調度問題中，通過犧牲少量的成本優化來降低干擾事件對老人和服務人員的影響，能夠推動虛擬養老院健康發展。

4 結論

針對虛擬養老服務人員調度問題，本文從確定性調度優化和不確定性調度優化展開了研究。針對求解模型，在確定性優化過程中，本文以成本最優為優化目標構建初始調度模型，用于模擬理想狀態下調度求解。在不確定優化調度中即應對各種干擾事件的實時調度，本文首先通過分析干擾事件對各主體的影響，參考前景理論的價值函數建立擾動度量函數用于度量擾動大小，并以各方擾動度量最小為目標在初始調度方案的基礎上建立干擾管理模型；針對求解算法，本文通過改進灰狼優化算法的初始化狼群和位置更新公式，引入三種鄰域搜索算子和非支配排序設計了遺傳灰狼優化算法和多目標灰狼優化算法，用于本文兩個模型求解，通過求解標準算例驗證了算法的優越性。針對考慮的干擾事件，本文除了考慮時間窗變動和客戶需求變動外，還考慮了緊急狀況下的方案調整，使得更加契合智慧化養老模式；最后本文將干擾管理模型的結果與重調度結果進行對比，驗證了模型優越性。綜合來看本文的干擾管理模型能夠幫助虛擬養老院在面對干擾事件時，能夠均衡各方的利益從而合理的調整調度方案。作為智慧化養老的靚麗名片，在未來，虛擬養老院一定會逐漸被更多老人所認可和接受。從學術角度來看，虛擬養老院的服務內容將更為廣泛，如何做好供需匹配，避免資源浪費將是研究的重點。此外，考慮到服務對象的特殊性，實際服務中所面臨的干擾事件將更為復雜，隨機性也會更強，未來更多面對的是不確定優化甚至是深度不確定性優化，因此如何隨機模擬干擾情境，識別干擾事件擾動影響，針對各種干擾事件做出調整尤為重要。此外，社區作為養老的重要依托，根據社區老人的年齡、身體狀況等因素實現重點區域劃分，設置量化的風險系數，及時響應老人需求變動將是接下來的研究重點。

參考文獻：

［1］BEGUR S B， MILLER D M， WEAVER J R. An integrated spatial dss for the scheduling and routing home-health-care nurses［J］. Interfaces， 1997， 27（4）： 3548.

［2］EUCHI. J. Optimising the routing of home health caregivers： can a hybrid ant colony metaheuristic provide a solution？［J］. British Journal of Healthcare Management， 2020， 26（7）： 192196.

［3］TABOUMAND T， UNLUYURT T. An exact algorithm for the resource constrained home health care vehicle routing problem［J］. Annals of Operations Research， 2021，304（1/2）： 129.

［4］DECERLE J， GRUNDER O， HAJJAM EI HASSANI A， et al.A general model for the home health care routing and scheduling problem with route balancing［J］. IFAC PapersOnLine， 2017， 50（1） 1466214667.

［5］HADDADENE S R A，LABADIE N， PRODHON C. Bicriteria vehicle routing problem with preferences and timing constraints in home health care services［J］. Algorithms， 2019， 12（8）： 152152.

［6］袁彪，劉冉，江志斌，等.隨機服務時間下的家庭護理人員調度問題研究［J］.系統工程理論與實踐，2015，35（12）：30833091.

YUAN B， LIU R， JIANGZ B， et al. Home care crew scheduling problems under service time uncertainty［J］. Systems Engineering-Theory & Practice. 2015， 35（12）： 30833091.

［7］楊欣潼，張婷，白麗平，石園，等.社區居家養老服務的預約調度與路徑規劃問題研究：基于改善蟻群算法［J］.系統工程理論與實踐，2019，39（5）：12121224.

YANG X T， ZHANG T， BAI L P， et al. Appointment scheduling and routing problem of community-home-health-care： based on modified ant-colony algorithm［J］. Systems Engineering-Theory & Practice. 2019， 39（5）：12121224.

［8］任宗偉，劉鈺冰.考慮老年人感知滿意度的社區居家養老護理人員調度策略研究［J］.運籌與管理，2022，31（8）：232239.

REN Z W， LIU Y B. Research on scheduling strategy of community home care nursing staff considering the elderly perception satisfaction［J］. Operations Research and Management Science， 2022， 31（8）： 232239.

［9］丁鋒， 付亞平， 王偉， 王洪峰. 多中心社區居家養老服務調度與服務網絡優化［J］. 復雜系統與復雜性科學， 2022， 19（1）： 104110.

DING F， FU Y P， WANG W， et al. Multi-depot scheduling and service network optimization problem of community home health care［J］. Complex Systems and Complexity Science， 2022， 19（1）： 104110.

［10］ SHI Y， BOUDOUH T， GRUNDER O. A hybrid genetic algorithm for a home health care routing problem with time window and fuzzy demand［J］. Expert Systems with Applications， 2017， 72： 160176.

［11］ YUAN B， JIANG ZB. Disruption management for the real-time home caregiver scheduling and routing problem［J］. Sustainability， 2017， 9（12）： 2178.

［12］ CAPPANERA P，SCUTELLA M G， NERVI F， et al.Demand uncertainty in robust home care optimization［J］. Omega， 2018， 80： 95110.

［13］ BAZIRHA M， KADRANI A， BENMANSOUR R. Stochastic home health care routing and scheduling problem with multiple synchronized services［J］. Annals of Operations Research， 2021，320（2）： 129.

［14］JAMES C. BEAN; JOHN R. BIRGE， JOHN MITTENTHAL， et al. Scheduling with multiple resources， release dates and disruptions［J］. Operations Research， 199 39（3）： 470483.

［15］ GANG Y， XIANG Q. Disruption Management： Framework， Models and Applications ［M］. Singapore： World Scientific Publishing， 2004.

［16］ NING T，SHI S S， ZHANG P， et al. Disruption management decision model for VRPSDP under changes of customer distribution demand［J］. Journal of Ambient Intelligence and Humanized Computing， 202 12： 20532063.

［17］ SANG Y W， TAN J P， LIU W. A new many-objective green dynamic scheduling disruption management approach for machining workshop based on green manufacturing［J］. Journal of Cleaner Production， 202 297：126489.1126489.15.

［18］HICHAM R， BADR A E M， MOHAMMED B. Airline schedule disruption management. the impact of flight delays on connection loss［J］. MATEC Web of Conferences， 2017， 105： 00013.

［19］ MALUCELLI F， TRESOLD E. Delay and disruption management in local public transportation via real-time vehicle and crew re-scheduling： a case study［J］. Public Transport， 2019， 11（1）： 125.

［20］ KAHNEMAN D， TVERSKY A.Prospect theory： an analysis of decision under risk［J］. Econometrica， 1979， 47（2）： 263291.

［21］ 戚銘堯，張金金，任麗.基于時空聚類的帶時間窗車輛路徑規劃算法［J］.計算機科學，2014，41（3）：218222

QI M Y， ZHANG J J， REN L.Vehicle routing algorithm based on spatiotemporal clustering［J］. Computer Science， 2014， 41（3）： 218222.

［22］ MIRJALILIS S， MIRJALILI S M， LEWIS A. Grey wolf optimizer［J］. Advances in Engineering Software， 2014， 69： 4661.

［23］ SOLOMON M M. Algorithms for the vehicle routing and scheduling problems with time window constraints［J］. Operations Research， 1987， 35（2）： 254265.

（責任編輯 李 進）