基于灰色關聯度的某畜禽車車廂多目標優化

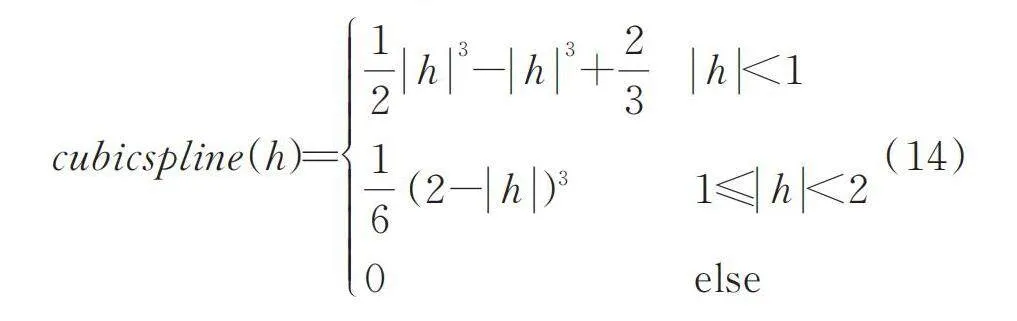
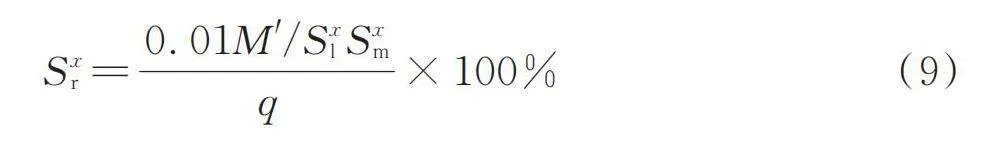
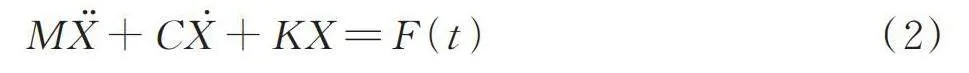
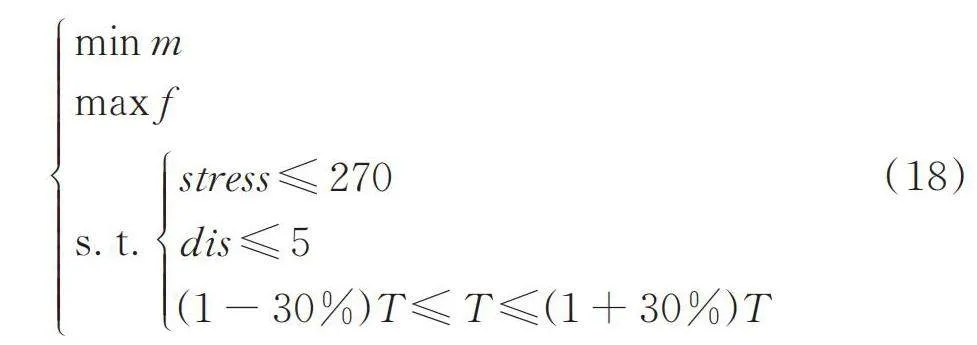
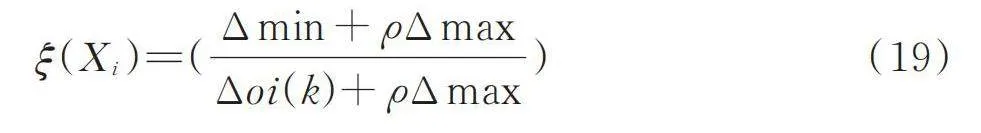
摘要：為降低某公司4×2畜禽運輸車的生產成本以及提高車輛的燃油經濟性，在保證車廂結構性能的前提下，對畜禽車車廂進行輕量化設計。通過對車廂進行靜態分析和動態分析，了解其結構性能后，使用混合靈敏度方法從80組設計變量中篩選出30組設計變量，再用哈默斯雷法Hammersley對設計變量進行采樣；隨后使用移動最小二乘法MLSR創建近似模型，并通過確定系數來判斷擬合精度；最后使用多目標遺傳算法MOGA對近似模型進行優化并得到帕雷托前沿，并基于灰色關聯度分析從該帕雷托前沿中篩選出一組最優板厚。優化后的模型在保證車廂整體結構性能的前提下使車廂減重6.8%，并且一階模態頻率提高2.9 Hz。

關鍵詞：畜禽車車廂；近似模型；多目標優化；帕雷托前沿；灰色關聯度

中圖分類號：U463 文獻標識碼：A 文章編號：2095?5553 （2024） 11?0131?08

Multi?objective optimization of a livestock and poultry vehicle carriage based on

grey correlation degree

Zhao Tieqi， Gong Yunxi， Fu Aijun， Zhang Guoshun， Zhang Jian

（School of Mechanical and Automotive Engineering， Guangxi University of Science and Technology， Liuzhou， 545000， China）

Abstract： In order to reduce the production costs and enhance the fuel economy of a company's 4×2 livestock and poultry transport vehicle， on the premise of ensuring the structural performance of the livestock and poultry vehicle， lightweight design of the compartment was carried out. Static and dynamic analysis of the compartment were conducted to understand its structural performance. A mixed sensitivity method was used to select 30 design variables from 80， followed by Hammersley sampling for these variables. An approximate model was created by using mobile least squares regression （MLSR）， and its fitting accuracy was determined by the coefficient of determination. The model was optimized by using a multi?objective genetic algorithm （MOGA） to obtain the Pareto frontier. Based on gray correlation analysis， a set of optimal plate thicknesses was selected from the Pareto frontier. The optimized model resulted in a 6.8% reduction in compartment weight while maintaining overall structural performance， and the first?order modal frequency increased by 2.9 Hz.

Keywords： livestock and poultry vehicle carriage; approximate model; multi?objective optimization; Pareto frontier; grey correlation degree

0 引言

隨著畜牧業的快速發展，畜禽運輸成為畜牧業中必不可少的一部分。但是由于新生仔畜的環境適應能力較弱，車身的結構破壞和共振均會引起畜禽在運輸中應激，從而導致畜禽的免疫水平和生產能力的下降[1]。同時過大的車廂質量不僅會增加畜禽車在行駛時的油耗，而且會影響滿載時車廂的結構強度。所以目前畜禽車著重研究在保持車廂良好結構性能的前提下對其進行結構輕量化，同時盡可能高的提高車廂的一階固有頻率以避開由路面激勵頻率或者發動機怠速頻率引起的車廂共振。謝虎等[2]以農用運輸車的車架厚度為設計變量，采用拓撲優化的方法將車架的一階固有頻率提高至6.35 Hz，避開了外部激勵頻率；張健等[3]通過優化車架縱梁的橫截面積，在滿足車架結構性能的前提下減重了19.5%；郭冬青等[4]通過對橋殼結構進行改進，不僅減小了零部件危險結構的靜應力和瞬態動位移，并且提高了固有頻率，達到了優化要求。

本文在不改變畜禽車車廂整體結構的前提下，通過改變車廂的板厚來達到輕量化的目的。首先使用混合靈敏度分析篩選出對車廂質量影響較大、模態和剛度影響較小的30組設計變量，再使用試驗設計DOE擴大設計變量的樣本數并生成采樣點，再通過對采樣點擬合生成的近似模型進行多目標優化，最后通過灰色關聯度分析GRA篩選出一組合適的板厚，帶入優化模型驗證優化后車廂結構性能和方案的可行性。

1 車廂有限元分析

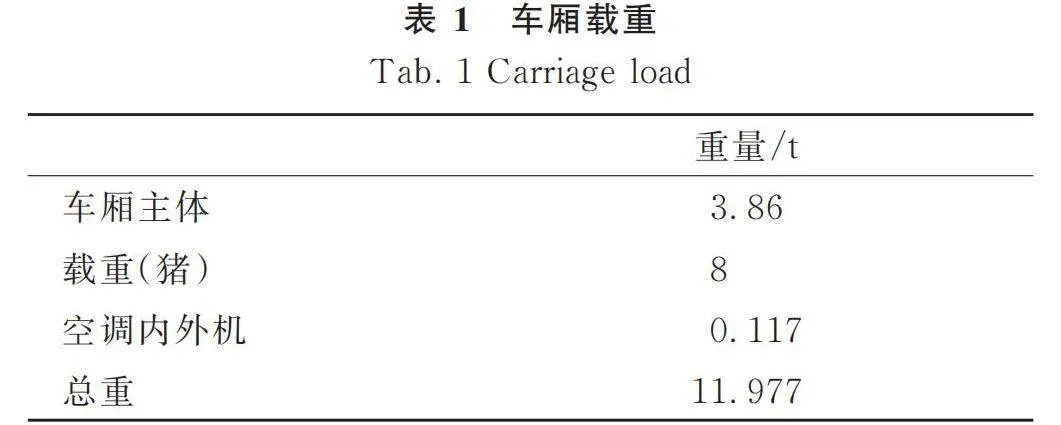
根據提供的三維畜禽車模型，導入有限元軟件中并進行前處理：劃分網格、適當簡化模型、材料設置、設置約束和設置工況。車廂主體采用10 mm和20 mm SHELL單元模擬，忽略不參與受力的零件。車廂主體重量為3.86 t，8 t的畜禽分布在3層中間板和底板上，車廂前半部分加裝了空調內外機和空調側板活動門，車廂頂部安裝了可升降頂蓋，其主體質量如表1所示；車廂主體采用6060AL鋁合金，車廂支撐架采用Q235，副車架采用LG700XL，材料參數如表2所示；副車架約束與大梁相接觸的平動自由度，以及連接副車架和大梁螺栓的全部自由度；工況設置靜態特性和動態特性分析。

為了方便后文篩選設計變量，故將車廂的板件以厚度和所處位置進行分組，并以T1～T80進行命名。

1.1 靜態特性分析

靜態特性主要分析車廂在垂直工況、轉向工況和制動工況下的結構性能，其兩個主要重要指標分別是強度和剛度。

當車廂強度不足時，發生的破壞多為塑性變形，造成結構失效和材料的疲勞斷裂，進而影響車身的整體結構性能，降低車廂的模態頻率，引起共振，從而導致畜禽應激。所以車廂的最大應力應小于材料的許用應力，按照企業規定，車廂的安全系數n=1.5，材料的許用應力如表3所示；車廂剛度是評判車廂在受到外力后，抵抗其彈性變形的能力。按照企業規定，車廂的整體位移要小于10 mm。

1.1.1 垂直工況

垂直工況分析畜禽車駛過坑洼不平的路面時，此時畜禽和車廂會產生沖擊載荷，動載系數設定為2。副車架約束與大梁相接觸部分的平動自由度，以及連接副車架和大梁螺栓的全部自由度。分析結果如圖1、圖2所示。

1.1.2 制動工況

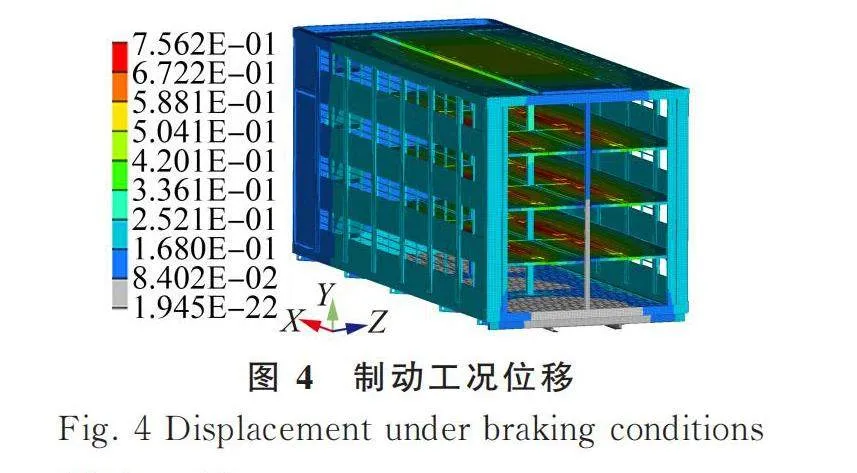
制動工況分析畜禽車緊急制動時，此時畜禽和車廂會由于慣性產生向前的沖擊載荷，動載系數設定為0.7。約束情況和垂直工況相同，分析結果如圖3、圖4所示。

1.1.3 轉向工況

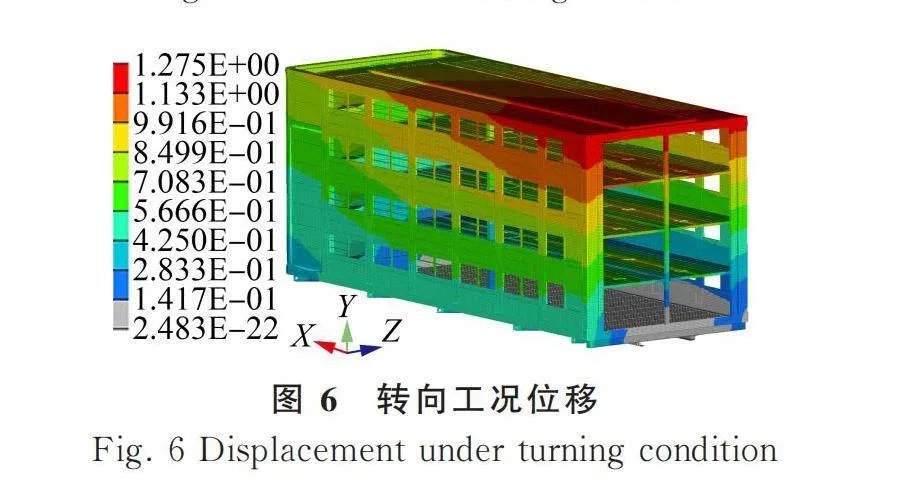
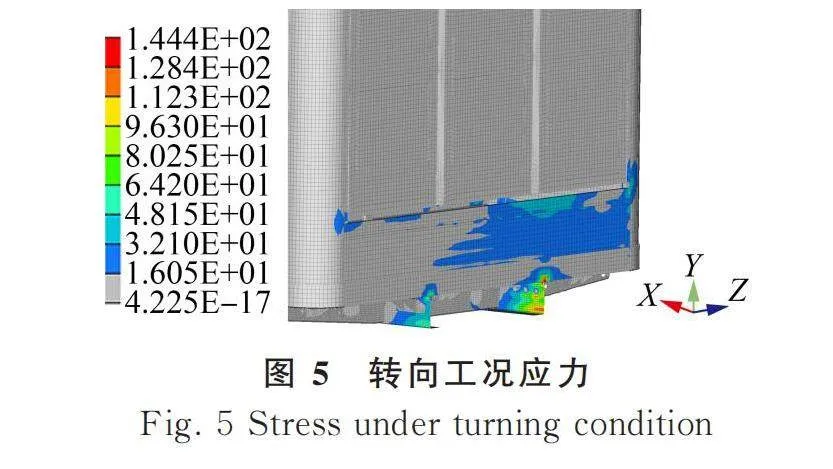
轉向工況分析畜禽車在路面轉彎時，畜禽和車廂會由于離心力產生向轉彎方向的載荷，動載系數設定為0.4，約束情況和垂直工況相同，分析結果如圖5、圖6所示。

1.1.4 計算結果分析

該畜禽車在三種工況下的應力和位移如表4所示。

由表4可知，三種工況的最大應力位于垂直工況的縱梁上，但小于材料LG700XL的許用應力，滿足強度指標要求；最大位移仍是垂直工況，為1.6 mm，小于設計目標值10 mm，滿足剛度指標要求。

1.1.5 模態分析

畜禽車的車廂為多自由的振動系統，一旦車廂的固有頻率和外界頻率重合，車廂就會發生共振。引起共振的因素主要有兩種：（1）道路的激勵頻率；（2）發動機怠速運轉時的頻率。由于我國的道路激勵頻率一般在3 Hz以下，故本文主要考慮車廂在發動機怠速運轉時的頻率[5]。

此畜禽車的發動機為六缸四沖程發動機，轉速為600 r/min，其激勵頻率f計算如式（1）所示。

[f=2nz60τ] （1）

式中： n——畜禽車發動機的額定轉速，r/min；

z——發動機的氣缸數；

τ——發動機的沖程數。

代入數據求得，該畜禽車的發動機怠速運轉時的頻率為30 Hz。

由于畜禽車車廂為多自由度的振動系統[6]，其振動微分方程的表達式為

[MX+CX+KX=F（t）] （2）

式中： M——質量；

C——阻尼；

K——剛度矩陣；

X——位移向量

[F（t）]——激勵向量。

本文研究的是畜禽車的自由模態，即不考慮外界載荷和約束條件，阻尼C和外界激勵頻率F（t）為0，式（2）可簡化為

[MX+KX=0] （3）

由于該振動方程為常系數線性齊次微分方程，故其解X為

[X=x1sin（ωt+φ）] （4）

式中： x1——模態矩陣；

ω——固有頻率；

[φ]——振動初始相位。

將式（4）帶入式（3）中，可以求得特征值ω2，即固有頻率ω。

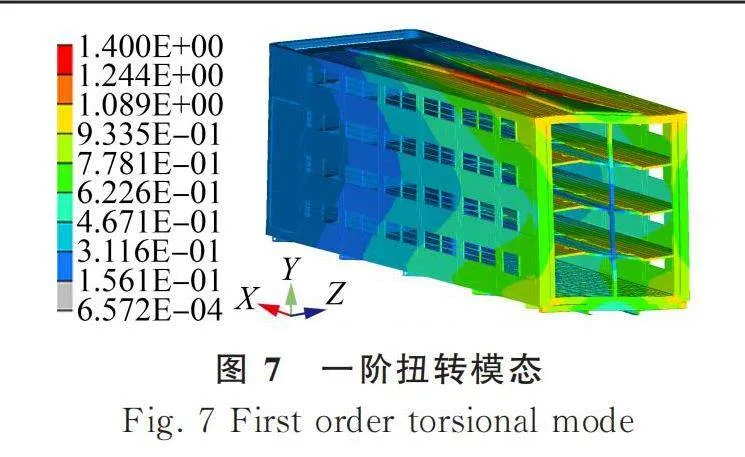
在分析該畜禽車的自由模態時，首先要過濾掉車廂的剛體模態，分析廂體骨架模型的前10階彈性自由模態，如表5所示。車廂的一階扭轉模態如圖7所示，車廂的一階彎曲模態如圖8所示。

由表5可知，該畜禽車的第一階模態頻率為32.9 Hz，避開了發動機的怠速頻率，故在后續優化過程中應盡可能提高車廂的一階模態固有頻率以避開由路面激勵頻率或者發動機的怠速頻率而引起的車廂共振。

由畜禽車車廂的靜態分析和動態分析結果可知：車廂在三種工況下應力和位移均在設計目標內；車廂的前10階模態頻率避開了發動機怠速運轉時的頻率，所以該畜禽車車廂具有較大的優化空間。

2 車廂設計變量的確定

在對車廂結構進行輕量化設計時，改變不同部件的厚度對車廂的整體結構性能的影響是不確定的；同時，對車廂的80組設計變量逐一進行優化計算量非常龐大，故采用靈敏度分析的方法來篩選設計變量[7]。

2.1 直接靈敏度分析

直接靈敏度分析[8]可以用來反應各個設計變量對性能參數的影響程度，也是設計響應對優化變量的偏導數。

靜力學的有限元平衡方程為

[YU=Z] （5）

式中： Y——剛度矩陣；

U——位移向量；

Z——載荷向量。

對優化變量xt求偏導數得

[?Y?xtU+Y?U?xt=?Z?xt] （6）

由于載荷是固定的，故整理式（6）后可得位移靈敏度[9]

[SY=?Y?xt=-U-1?U?xtY] （7）

分別選取車廂的前30組較大的模態和位移的靈敏度，其中紅色代表正相關，藍色代表負相關（圖9、圖10）。

直接靈敏度分析雖然可以篩選出對單個性能指標影響較大的設計變量，但是卻很難在多組性能指標中篩選出對性能影響較小及對質量影響較大的設計變量，故引入混合靈敏度方法來篩選設計變量。

2.2 平均相對靈敏度

平均相對靈敏度意味著在原有車廂板厚的基礎上，每組厚度改變1%時車廂結構性能改變的比值，計算如式（8）所示。

[Sa=i=1n0.01txSxl×100%] （8）

式中： tx——第x組零件的厚度；

[Sxl]——第x組設計變量位移和模態靈敏度。

計算可得模態的平均相對靈敏度為12.23%，剛度的平均相對靈敏度為-9.62%。

2.3 相對靈敏度

相對靈敏度的方法和平均相對靈敏度的方法相似，但是相對靈敏度[10]是通過改變一組設計變量使得車廂的整體質量增加1%時車廂結構性能該改變的比值，計算如式（9）所示。

[Sxr=0.01M'/SxlSxmq×100%] （9）

式中： M'——車廂不同設計變量的質量總合；

[Sxm]——第x組設計變量的質量靈敏度；

q——車廂結構的初始狀態性能。

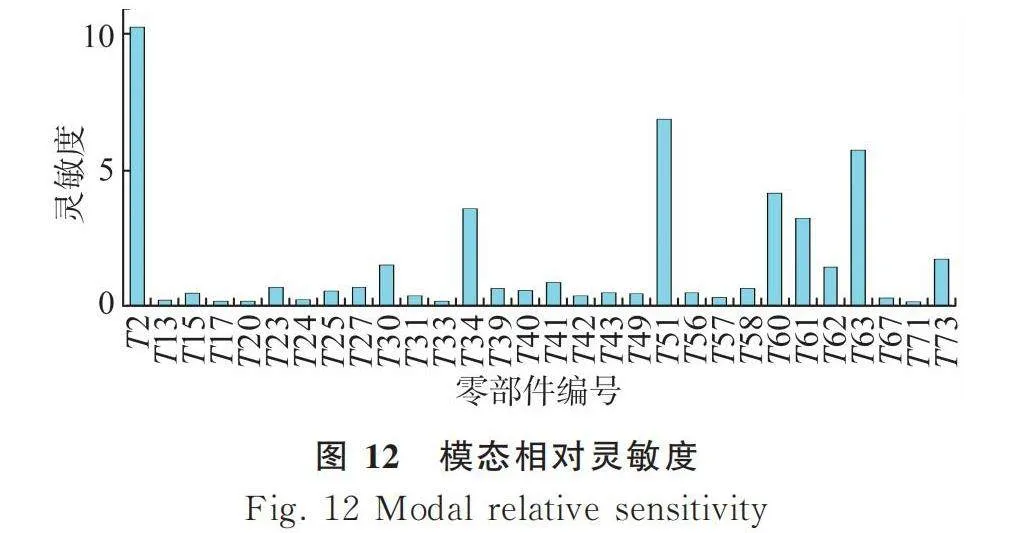
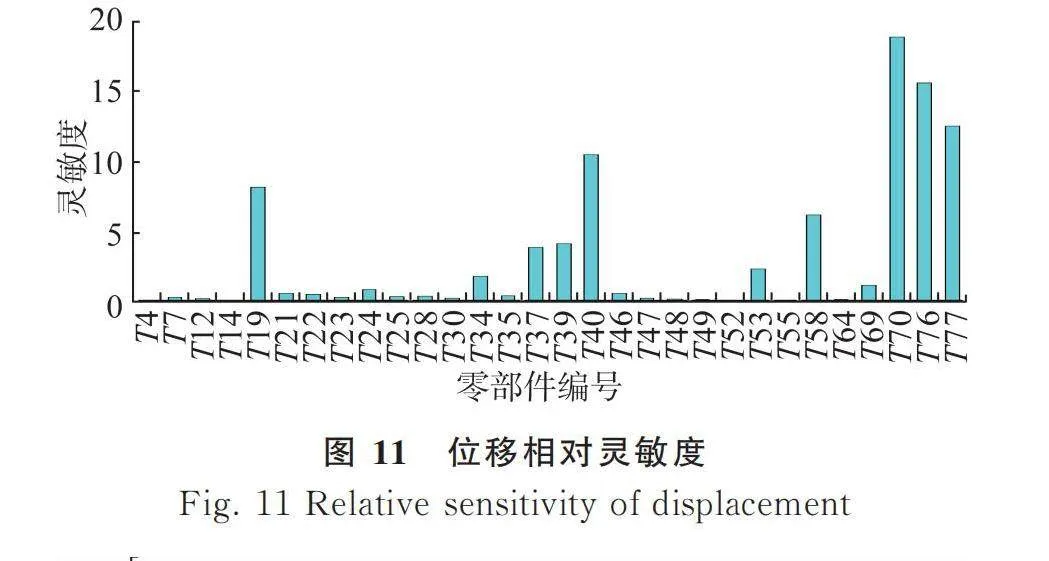
選取車廂的前30組較大的模態和剛度的相對靈敏度，其中紅色代表正相關，藍色代表負相關，如圖11、圖12所示。

通過比較平均相對靈敏度和相對靈敏度的大小來判斷一組設計變量對車廂結構性能的影響程度[11]。當平均相對靈敏度較大時，該零部件厚度的改變對車廂整體結構性能影響較小，該零部件可以進行優化；當相對靈敏度較大時，該零部件厚度的改變對車廂整體結構性能影響較大，此時需判斷是否進行優化[12]。

3 車廂結構優化

工程結構的優化問題，實質就是用數學模型來表達結構的力學模型[13]。該畜禽車的優化求解的目標為車廂的質量最小和第一階模態頻率最大，設計約束為車廂的位移和應力均處在設計目標內。

3.1 試驗設計

試驗設計的本質是通過正交試驗來揭示不同的影響因子對響應的影響，不僅可以了解各因子對響應影響程度的大小，還可以在設計空間內取得均勻分布的樣本點進行響應面的生成。

該車廂使用哈默斯雷采樣法Hammersley[14]，因為該方法相比拉丁超立方算法在k維超立方體上樣本點能取得更好分布，近似模型的精度更高。Hammersley點（xi，yi）在二維空間中可由式（10）、式（11）表示。

[xi=iM] （10）

[yi=k=0z-1i2kmod2×2-k-1]

[0≤xi，yi≤1]，[i=0，1，…，M-1] （11）

式中： M——采樣點的總數目，[z=log2M]，代表不小于[log2M]的最小整數；

[i2k]——不大于它的最大整數。

使用Hammersley算法對篩選后的設計變量進行200次的運算矩陣。

3.2 響應面擬合

根據Hammersley算法設計的200次的運算矩陣，采用MLSR（移動最小二乘法）算法創建響應面[15]。

移動最小二乘法是形成無網格方法逼近函數的方法之一：在離散的點云中，當知道曲線曲面的形式時，可以用最小二乘法來進行擬合；當不知道曲線曲面的具體形式時，可以使用移動最小二乘法來進行擬合。

MLSR法中的擬合函數并不是傳統最小二乘法中的一個多項式，而是一組向量函數[aj（h）]和基函數[pj（h）]，則某個節點node附近的擬合函數為

[unode（h）=j=1maj（hnode）×pj（h）] （12）

式中： [hnode]——節點的空間坐標；

h——節點node附近的某一個位置坐標；

aj——定義節點node附近擬合曲線的一組系數；

pj——基函數。

在MLSR方法中，為了使節點node附近采樣點取值與擬合函數在采樣點之間差的加權平方和最小，故加入提調整系數a來建立優化模型為

[Y=r=1nw（hnode-hr）u（hnode）-hr2=r=1nw（hnode-hr）j=1maj（hnode）×rj-ur2] （13）

式中： r——采樣點；

hr——采樣點r的空間位置；

ur——采樣點r的取值；

w——權函數。

權函數其常用形式如式（14）所示。

[cubicspline（h）=12h3-h3+23h<116（2-h）31≤h<20else] （14）

式（14）表示對函數Y的貢獻越大，則w權函數可以保證該采樣點距離node越近；距離較遠的點則不會對函數Y產生影響。

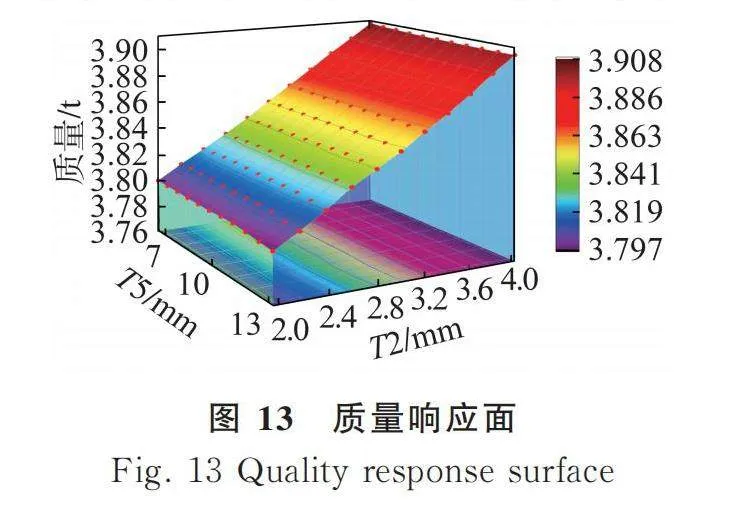
選擇設計變量T2和T5，通過移動最小二乘法擬合的質量和模態的響應面，如圖13、圖14所示。

由于設計變量和控制目標較多，故響應面沒有明確的數學表達式，只能通過圖形來判斷擬合的精準度，且優化結果的可信度也取決于近似模型的精準度，近似模型的精度越高，優化結果越可靠[16]。模型的精度判斷一般用確定系數R2、均相對誤差RAAE和均方根差RMSE來判斷。R2越接近1，RAAE和RMSE越接近0，則模型的精度越高。

R2、RAAE和RMSE的計算如式（15）～式（17）所示。

[R2=i=1N（yi-yi）2i=1N（yi-y）2] （15）

[RAAE=1Ni=1Nyi（x）-yi（x）yi（x）] （16）

[RMSE=i=1N（yi（x）-yi（x））2N-1] （17）

式中： ?i——響應的實測值；

yi——響應的預測值；

[yi]——響應的實測值的平均值；

N——樣本數目。

樣本點響應誤差統計，如表6所示。由表6可知，質量、模態、位移和應力的近似模型的確定系數都接近于1，均相對誤差和均方根差都接近于0，意味著優化結果均非常可靠，可以用作優化。

3.3 多目標優化

對該畜禽車車廂進行優化，要保證車型在質量最小的前提下，一階模態要盡可能的提高以避開發動機的怠速頻率，車廂的應力和位移要處在企業規定范圍內。故該車廂的多目標優化問題[17]可以總結為式（18）。

[min mmax fs.t.stress≤270dis≤5（1-30%）T≤T≤（1+30%）T] （18）

式中： m——畜禽車的質量；

f——畜禽車一階自由模態的頻率；

stress——畜禽車的最大應力；

dis——畜禽車的最大位移；

T——設計變量的厚度。

采用MOGA（多目標遺傳算法）對基于響應面的近似模型進行求解，得到帕雷托前沿[18]如圖15所示。

通過MOGA算法對近似模型進行優化，得到該畜禽車設計變量的帕雷托解集[19]，該解集意味著在有多個目標的情況下，不存在比當前解更好的解決方案。在該解集中，可能會存在一組數據能夠滿足所有的優化目標，但大部分情況下各個優化目標是相互沖突的，提高一個優化目標的性能勢必會降低另一優化目標的性能，即不存在一個解同時滿足所有優化目標的情況。這時可以使用灰色關聯法在帕雷托前沿上進行決策和選擇，找到最優解。

3.4 灰色關聯度分析

由于車廂的質量和模態受其他因素影響的相對強弱，所以可以通過GRA（灰色關聯度分析）來從帕雷托前沿中找到一組合適的板厚[20]。

首先將帕雷托前沿中的數據變化為決策矩陣，通過將這個矩陣標準化得到評價矩陣，將評價矩陣的最優值構成參數數據列，再逐個計算每個被評價對象指標序列與參考序列對應元素的絕對值差。通過求得每行的最小值和最大值計算矩陣的關聯系數

[ξ（Xi）=（Δmin+ρΔmaxΔoi（k）+ρΔmax）] （19）

式中： [Δmin]——評價矩陣每行的最小值；

[Δmax]——評價矩陣每行的最大值；

[Δoi（k）]——各比較數列上的每一個點與參考數列上的每一個點的絕對差值；

ρ——分辨系數，ρ>0，通常取0.5。

由于關聯系數呈現的是數列與參考數列的關聯程度，并且關聯系數不止一個且過于分散，難以進行比較，故引入比較數列與參考數列間關聯程度的數量的關聯度

[ri=1Nk=1Nξi（k）] （20）

式中： N——矩陣的列數；

k——每行的數據。

最終求得該帕雷托前沿的關聯度[21]，如表7所示。

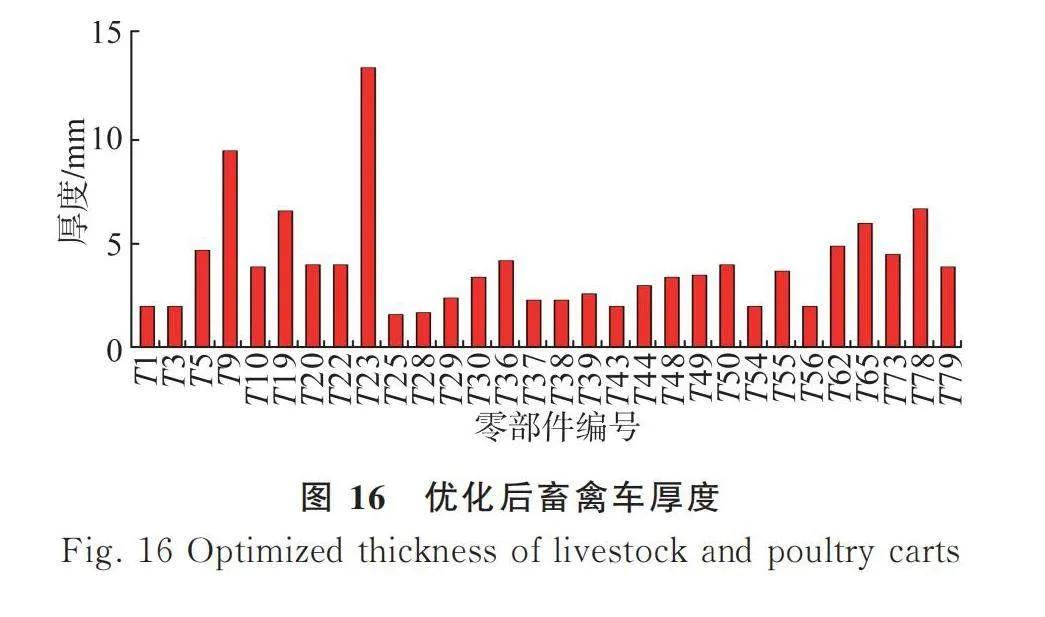
由表7可知，第36組數據的關聯度最高，為0.666 6，其圓整后的數據如圖16所示，并代入原畜禽車模型進行驗證。

3.5 優化結果與分析

基于建立的近似模型，使用多目標遺傳算法對畜禽車的各板厚進行優化，采用灰色關聯度分析在帕雷托前沿中尋找到一組最優的板厚，圓整后代入到原畜禽車車廂模型中，優化后的畜禽車車廂各結構性能如表8所示。

由表8可知，在保證畜禽車車廂結構性能的前提下，質量減小了0.26 t，減重率達6.8%；第一階模態頻率提升了2.9 Hz，車廂的最大應力處在垂直工況的縱梁上，為235.4 MPa，仍小于材料LG700XL的許用應力；最大位移為2.1 mm，滿足剛度指標要求。

4 結論

1） 通過對畜禽車車廂進行靜態和動態特性分析，了解到原畜禽車車廂的最大應力和位移均處在垂直工況下，應力為167.2 MPa，位移為1.6 mm，但均處在設計目標內；模態分析下原畜禽車車廂的一階自由模態為32.9 Hz，避開該畜禽車發動機的怠速頻率和大部分道路激勵頻率，確定該車廂具有較大的優化空間。

2） 使用混合靈敏度方法對車廂的設計變量進行篩選，從80組設計變量中篩選出30組設計變量，并使用試驗設計對篩選后的設計變量進行200次矩陣運算，再使用MLSR算法創建近似模型，最后使用多目標遺傳算法對搭建的近似模型進行優化，最終得到帕雷托前沿。

3） 由于帕雷托前沿是該車廂最優解的解集，故使用灰色關聯度分析從解集中篩選，其中第36組板厚數據的關聯度最高，為0.666 6。對篩選后的板厚進行圓整并再次進行靜力學分析和動力學分析，在保證車廂結構性能的前提下，最終車廂減重6.8%，且一階模態頻率提高了2.9 Hz，驗證了優化方案的可行性。

參 考 文 獻

[ 1 ] 張國平， 趙碩， 阿麗瑪， 等. 肉羊運輸應激及其危害[J]. 家畜生態學報， 2017， 38（12）： 83-86.

Zhang Guoping， Zhao Shuo， Alima， et al. Analysis on the transportation stress of mutton sheep and its harm [J]. Acta Ecologiae Animalis Domastici， 2017， 38（12）： 83-86.

[ 2 ] 謝虎， 黃雪濤， 韓柏和， 等. 基于拓撲優化的農用運輸車輛減振技術研究[J]. 中國農機化學報， 2020， 41（1）： 104-108.

Xie Hu， Huang Xuetao， Han Baihe， et al. Vibration reduction technology analysis of agricultural transport vehicle based on topology optimization [J]. Journal of Chinese Agricultural Mechanization， 2020， 41（1）： 104-108.

[ 3 ] 張健， 陳科任， 代艷萍. 面向現代農業莊園的電動車車架設計及模態分析[J]. 中國農機化學報， 2019， 40（2）： 109-112.

Zhang Jian， Chen Keren， Dai Yanping. Design and modal analysis of electric vehicle frame for modern agricultural manor [J]. Journal of Chinese Agricultural Mechanization， 2019， 40（2）： 109-112.

[ 4 ] 郭冬青， 張翠平， 姚曉博， 等. 農用車驅動橋殼的有限元分析與結構改進[J]. 中國農機化學報， 2015， 36（5）： 198-202.

Guo Dongqing， Zhang Cuiping， Yao Xiaobo， et al. Finite element analysis and structure improvements of agricultural vehicle driving axle housing [J]. Journal of Chinese Agricultural Mechanization， 2015， 36（5）： 198-202.

[ 5 ] 吳鵬興， 劉夫云， 宋超. 基于NSGA-Ⅱ的隱式參數化白車身輕量化設計[J]. 機械設計， 2022， 39（2）： 95-100.

Wu Pengxing， Liu Fuyun， Song Chao. Lightweight design of BIW based on NSGA-II implicit parameterization [J]. Journal of Machine Design， 2022， 39（2）： 95-100.

[ 6 ] 何睿. 基于多學科多目標的車架結構輕量化設計[J]. 噪聲與振動控制， 2022， 42（2）： 173-178.

He Rui. Lightweight design of frame structures based on multi?discipline and multi?objective [J]. Noise and Vibration Control， 2022， 42（2）： 173-178.

[ 7 ] Choi M J， Cho S. Isogeometric configuration design sensitivity analysis of geometrically exact shear?deformable beam structures [J]. Computer Methods in Applied Mechanics and Engineering， 2019， 351： 153-183.

[ 8 ] 康滿， 陸靜. 基于靈敏度分析的車門輕量化研究[J]. 科學技術與工程， 2016， 16（36）： 76-80.

Kang Man， Lu Jing. Research on the lightweight of car door based on sensitivity analysis [J]. Science Technology and Engineering， 2016， 16（36）： 76-80.

[ 9 ] 王震虎， 周巧英， 劉開勇， 等. 基于響應面模型的白車身多目標輕量化設計[J]. 中國機械工程， 2018， 29（1）： 75-81.

Wang Zhenhu， Zhou Qiaoying， Liu Kaiyong， et al. Multi?object lightweight design of BIWs based on response surface model [J]. China Mechanical Engineering， 2018， 29（1）： 75-81.

[10] 周松， 高翔， 張志， 等. 基于相對靈敏度的重型自卸車結構輕量化設計[J]. 科學技術與工程， 2021， 21（35）： 15027-15034.

Zhou Song， Gao Xiang， Zhang Zhi， et al. Lightweight design of dump truck structure based on relative sensitivity analysis [J]. Science Technology and Engineering， 2021， 21（35）： 15027-15034.

[11] 趙樹恩， 楊明森， 彭光旭. 基于NSGA-II混合靈敏度分析的白車身輕量化優化設計[J]. 機械強度， 2019， 41（4）： 887-894.

[12] 萬強， 阮景奎. 基于混合靈敏度分析的某自卸車車廂結構優化設計[J]. 科學技術與工程， 2020， 20（12）： 4954-4961.

Wan Qiang， Ruan Jingkui. Optimization design of dump truck structure based on mixed sensitivity analysis [J]. Science Technology and Engineering， 2020， 20（12）： 4954-4961.

[13] 劉鋒， 張瑞乾， 陳勇. 基于模態和剛度的車門輕量化研究[J]. 機械強度， 2021， 43（2）： 476-481.

[14] 李軍， 冷川. 基于RBF神經網絡模型的車門多目標輕量化設計[J]. 重慶交通大學學報（自然科學版）， 2019， 38（11）： 127-132.

[15] Jiang R， Ci S， Liu D， et al. A hybrid multi?objective optimization method based on NSGA-II algorithm and entropy weighted TOPSIS for lightweight design of dump truck carriage [J]. Machines， 2021， 9（8）： 156.

[16] 宋超， 匡兵， 劉夫云， 等. 基于靈敏度分析的商dX2WosfUQKLFB09BCM1jeDcdiLCAN2kAoSNdgn8bmdU=用車駕駛室白車身輕量化設計[J]. 現代制造工程， 2021（3）： 46-51， 126.

Song Chao， Kuang Bing， Liu Fuyun， et al. Lightweight design of commercial vehicle cab body?in?white based on sensitivity analysis [J]. Modern Manufacturing Engineering， 2021（3）： 46-51， 126.

[17] 邢志波， 譚繼錦， 汪小朋， 等. 多目標優化下汽車車門性能分析研究[J]. 合肥工業大學學報（自然科學版）， 2017， 40（7）： 888-891.

[18] Wang D， Jiang R， Wu Y. A hybrid method of modified NSGA-II and TOPSIS for lightweight design of parameterized passenger car sub?frame [J]. Journal of Mechanical Science and Technology， 2016， 30（11）： 4909-4917.

[19] 任明， 孫濤， 石永金， 等. 基于Kriging近似模型的車架輕量化優化[J]. 機械強度， 2019， 41（6）： 1372-1377.

[20] 王登峰， 李慎華. 基于Pareto挖掘的白車身側碰安全件輕量化優化設計[J]. 中國機械工程， 2021， 32（13）： 1584-1590， 1637.

[21] 蔣榮超， 劉大維， 王登峰. 基于熵權TOPSIS方法的整車動力學性能多目標優化[J]. 機械工程學報， 2018， 54（2）： 150-158.