基于改進魚群算法的牧場巡檢機器人路徑規劃研究

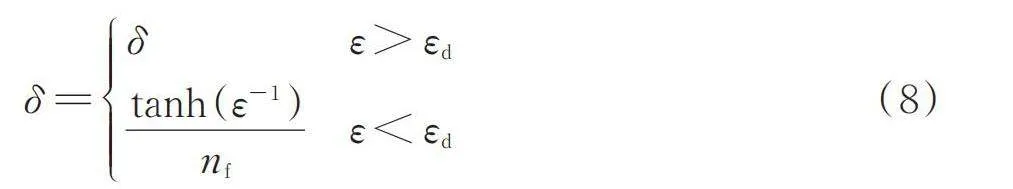
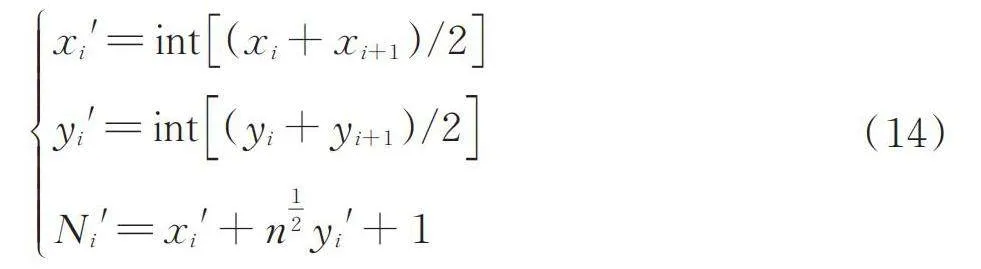
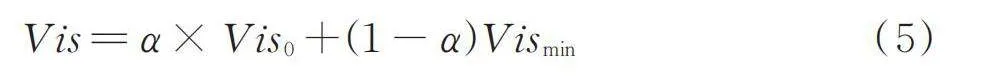
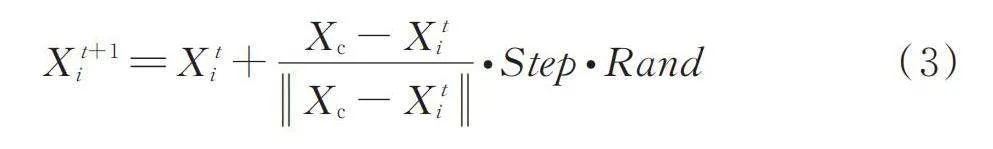
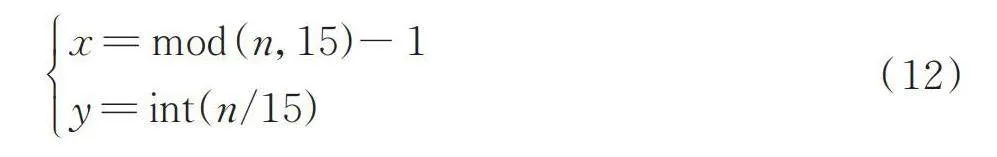
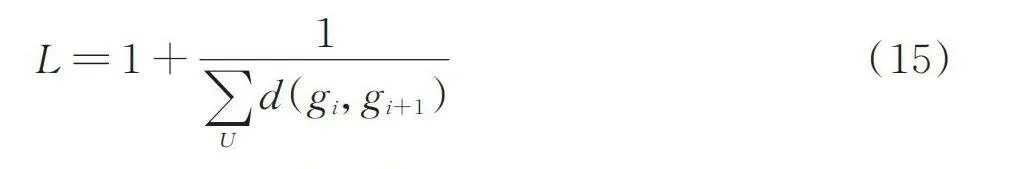
摘要：針對傳統人工魚群算法（AFSA）在牧場巡檢路徑規劃的過程中易陷入局部最優解、規劃的最優路徑較長等問題，提出一種改進人工魚群算法融合遺傳算法（GA）得到的遺傳魚群算法（GFSA）。GFSA在AFSA基礎上通過優化視野和步長，加快算法在求解過程中的收斂速度和精度；通過設計分段式擁擠度因子、引入遺傳算法中的變異操作，避免算法在迭代過程中過早聚集在局部最優解周圍。將GFSA搭載在牧場巡檢機器人上進行試驗驗證。結果表明，在消融試驗中，GFSA規劃的路徑長度均低于對比算法，其最優路徑長度中位數為23.2 m；在多算法對比試驗中，與對比算法相比，GFSA的路徑最短且轉彎幅度小；在不同障礙物率地圖的路徑規劃中，GFSA的最優路徑長度初始值、增長斜率均小于對比算法，具有更好的魯棒性和適應性。

關鍵詞：牧場；巡檢機器人；遺傳算法；人工魚群算法；路徑規劃

中圖分類號：S951 文獻標識碼：A 文章編號：2095?5553 （2024） 11?0202?07

Research on path planning of pasture inspection robot based on

improved fish swarm algorithm

Gao Jinzhe1， Kou Zhiwei1， 2， Xu Hanqi1， Duan Kehe1， Ma Jiayin1

（1. College of Electric Power， Inner Mongolia University of Technology， Hohhot， 010051， China;

2. Inner Mongolia Key Laboratory of Electromechanical Control， Hohhot， 010051， China）

Abstract： Aiming at the problems that traditional Artificial Fish Swarm Algorithm （AFSA） is easily falling into the local optimal solution and the planned optimal path is too long in the process of pasture inspection path planning， an improved Artificial Fish Swarm Algorithm integrated with Genetic Algorithm （GA） is proposed to obtain a Genetic Fish Swarm Algorithm （GFSA）. On the basis of AFSA， GFSA accelerates the convergence speed and accuracy during the solving process by optimizing the vision and step length. Additionally， the algorithm avoids premature convergence around local optimal solution during iterations by designing a segmented crowding factor and incorporating mutation operations from Genetic Algorithm （GA）. Genetic Fish Swarm Algorithm （GFSA） was implemented on a pasture inspection robot for experimental validation. The results showed that in ablation experiments， the path lengths planned by GFSA were consistently shorter than those of the comparison algorithms， with a median optimal path length of 23.2 m. In multi?algorithm comparison experiments， GFSA achieved the shortest paths and smaller turning angles compared to the other algorithms. In path planning on maps with different obstacle rates， GFSA's initial value and growth slope of the optimal path length were both lower than those of the comparison algorithms， demonstrating better robustness and adaptability.

Keywords： ranch; inspection robots; Genetic Algorithm （GA）; Artificial Fish Swarm Algorithm（AFSA）; path planning

0 引言

目前在牧場管理上，人工巡檢的方式仍占據主導地位，效率低、耗時長，難以滿足快速、高效的現代農業發展需求[1]。采用機器人進行牧場巡檢已經成為一個新的發展趨勢和研究熱點[2， 3]。但牧場巡檢機器人的路徑規劃問題仍是一個尚待解決的難題。

目前較為廣泛采用的技術路線是使用智能優化算法尋找路徑[4， 5]。但這類方法容易陷入局部最優解，計算復雜度相對較高[6]。Tian等[7]設計出一種基于模糊自適應遺傳算法的艦船避障路線規劃模型，測試結果顯示，該模型規劃出的路徑避障能力優于傳統模型。Zhang等[8]設計了一種基于各向異性快速行進算法的橋梁限制區內自主船舶路徑規劃方法，測試結果顯示，在橋梁限制區內，該算法所規劃的路徑較傳統方法更合理，且計算時間更短，為內陸橋梁區域自主船舶路徑規劃提供了重要參考。Xue等[9]提出了一種基于準反射的正弦余弦粒子群優化算法，用于船舶路徑規劃以避免觸地，仿真測試結果顯示，該算法相較于經典粒子群算法具有更快的收斂速率和更高的計算精度。Yan等[10]提出一種基于鯨魚優化算法的立體路徑規劃方法，結果顯示，該算法在規劃效率、執行時間、收斂速度和解決精度等方面表現出色，對水下立體空間路徑規劃任務具有顯著效果。Zhang等[11]提出了一種改進的局部粒子群優化算法，以解決移動機器人路徑規劃中局部最小值、過早收斂和低效率等問題，結果表明，該算法在路徑長度、運行時間、路徑優化性和穩定性等方面優于傳統方法，證明了其有效性、穩健性和可行性。Zhao等[12]提出了一種改進的人工魚群算法（Artificial Fish Swarm Algorithm，AFSA），引入方向操作符、概率權重因子、自適應操作符和路徑平滑器來提高自主表面艦艇路徑規劃的效率和質量，結果表明，該算法在效率和路徑質量方面優于其他算法，適用于實際應用。Li等[13]提出了一種基于約束理論的并行AFSA，用于解決傳統AFSA在搜索最優解時耗時長、容易陷入局部最優的問題，結果表明，與串行AFSA相比，該算法能夠有效減少搜索時間，并提高復雜多模態函數優化問題的搜索性能。

綜上所述，前人針對不同應用場景設計了多種高效路徑規劃模型，以提升規劃路徑的避障能力、效率或路徑長度。本文針對牧場環境下路徑規劃的過程中易陷入局部最優解、規劃的最優路徑較長的問題，提出一種改進人工魚群算法融合遺傳算法（Genetic Algorithm，GA）得到的遺傳魚群算法（Genetic Fish Swarm Algorithm，GFSA），GFSA在AFSA基礎上通過優化視野和步長、設計分段式擁擠度因子、引入遺傳算法中的變異操作，從而有效改善在牧場環境中路徑規劃過程中易陷入局部最優解、規劃的最優路徑較長的問題，從而提高牧場巡檢機器人的路徑規劃效果。

1 牧場巡檢機器人結構與原理

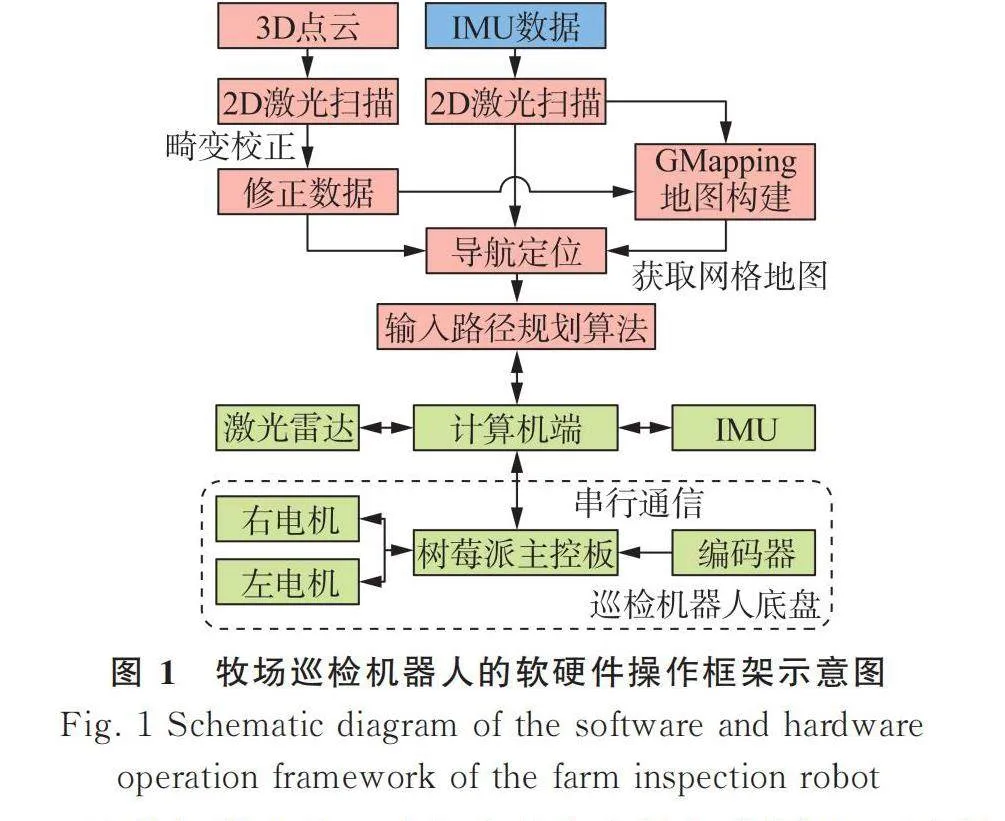
牧場巡檢機器人的軟件框架方面，使用GMapping（Grid?based FastSLAM Mapping）作為雷達數據建圖工具。但該工具只能用于二維雷達數據建圖，因此出現三維雷達數據時，使用ROS（Robot Operating System）的開源工具包Pointcloud_to_laserscan將數據形式降為二維。同時出于讓GMapping建圖更加準確的目的，還需要對二維LaserScan數據開展運動畸變矯正處理。設計出的牧場巡檢機器人軟件、硬件運行框架示意圖如圖1所示。

巡檢機器人的運動行為是由主控板控制的，而主控板通過與電腦端的無線連接，獲取電腦端的運動指令。在電腦端輸出的移動指令通過本文設計的混合GA的改進AFSA尋優得到。而路徑規劃所需的核心數據為巡檢機器人激光雷達系統收集到的環境信息以及根據這些信息生成的抽象圖像信息。這種抽象的圖像信息保留了有關路徑規劃的關鍵信息，比如障礙物、可移動范圍等，同時去除了對于路徑規劃無用的冗雜信息。

2 ROS和GSFA融合的路徑規劃設計

在能夠處理路徑規劃問題的智能算法中，AFSA具備搜索速度快、尋優能力強的優點，但易陷入局部最優解[14]。GA擁有優良的全局搜索能力，但也存在過于依賴初始種群的缺點[15]。嘗試將AFSA與GA結合起來，構建牧場巡檢機器人路徑規劃智能模型。

2.1 融合遺傳算法的改進人工魚群算法

本文中AFSA被用于優化輸出GA的初始種群，這也是兩者結合的方式。分析AFSA算法中魚群的行為特點，并從中引出該算法需要改進的方面。AFSA算法中魚群的行為分為覓食行為、聚群行為、追尾行為、隨機行為[16， 17]。覓食行為也即魚群自動聚集在食物密度最大區域的行為。

[Xti]為編號i的魚在t時刻的位置，Xj為魚群感知范圍內的選擇狀態，Xj計算如式（1）所示。

[Xj=Xti+Vis?Rand] （1）

式中： Rand（）——生成隨機數，取值范圍為[[0，1）]；

[Vis]——魚能看到的視野。

令[Y=f（x）]代表當前人工魚所處區域的食物濃度，Yi、Yj分別為人工魚當前所處區域的食物濃度、Xj位置的食物濃度，則人工魚在水下覓食行為描述為：若Yi<Yj，魚類向Yj位置移動，計算如式（2）所示。

[Xt+1i=Xti+Xj-XtiXj-Xti?Step?Rand] （2）

式中： Step——魚的移動步長；

[Xt+1i]——編號i的魚在t+1時刻的位置。

如果Yi<Yj不成立，會隨機選擇一個狀態，并繼續狀態分析比較。多次對比后評定條件仍然不滿足，人工魚群將進行隨機移動行為。

假設當前視野中的人工魚數量為[nf]、中心位置為Xc、中心位置對應食物濃度為Yc，擁擠度因子為δ。則群居行為可以描述為：當中心點食物濃度高且魚較少，也即滿足[Yc/nf>δYi]，魚會向著視野中心移動，這時[Xt+1i]計算如式（3）所示。

[Xt+1i=Xti+Xc-XtiXc-Xti?Step?Rand] （3）

如果人工魚Xj位置的食物濃度最高，為Yj，且[Yc/nf>δYi]，人工魚開始追尾行為，這時[Xt+1i]按式（2）計算。魚群在隨機行為下，[Xt+1i]計算如式（4）所示。

[Xt+1i=Xti+Vis?Step] （4）

AFSA在多次迭代后，收斂速度會大幅度降低，容易陷入局部最優解中，因此這里嘗試從多個方面改進該算法。首先優化AFSA的視野和步長，因為這兩個因素的選擇會影響魚的游動行為。傳統AFSA中視野和步長是固定的，導致算法迭代到后期尋優性能會衰減[18]。將視野和步長改為可變形式。改進后的視野計算如式（5）所示。

[Vis=α×Vis0+（1-α）Vismin] （5）

式中： [Vis0]——初始視野；

[Vismin]——最小視野；

α——中間變量。

[α=exp[-20（ddmax）5]] （6）

式中： d——當前迭代次數；

[dmax]——最大迭代次數。

改進后的步長計算如式（7）所示。

[Step=α?Step+0.3] （7）

式（7）組成結構是通過多次調試得到的。按以上方法，算法訓練的早期，步長和視野會更大，以保證算法搜索能力，訓練后期則可以通過較小的視野與步長以提升求解精度。

在擁擠度因子方面，采用分段方式設計擁擠度，試驗后得到的分段擁擠度d計算如式（8）所示。

[δ=δε>εdtanh（ε-1）nfε<εd] （8）

式中： δ——擁擠度因子；

ε——收斂誤差；

[εd]——收斂誤差閾值。

當ε向0收斂時，[tanh（ε-1）]收斂于1，則δ數值也將收斂于1。這時擁擠度因子幾乎不會發揮作用，以便防止訓練早期算法陷入局部解。訓練后期，魚群密度則不會受到限制，以縮短算法訓練時間，提升尋優效率。

式（8）應用雙曲正切函數[tanh（ ）]，計算如式（9）所示。

[tanh（w）=ew-e-we-w+ew] （9）

式中： w——輔助展示的變量符號。

AFSA迭代過程中，人工魚可能會聚集在極值點周圍，落入局部最優解，因此再對算法中的變異策略進行改進，使用式（10）更新變異概率m。

[m=mmin×cdmax] （10）

式中： [mmin]——變異概率的初始值；

c——當前公告牌未被更新次數。

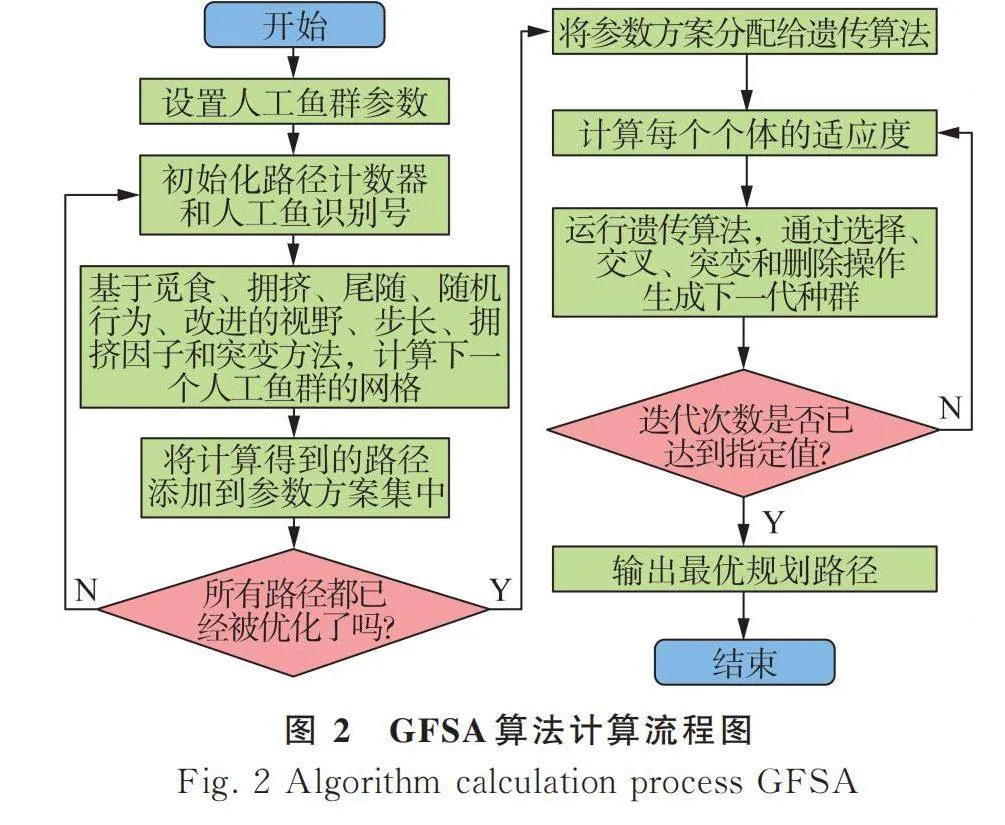
再將改進的AFSA與GA融合從而得到GFSA兩者結合后的計算流程見圖2。

2.2 GFSA搭載ROS的路徑規劃

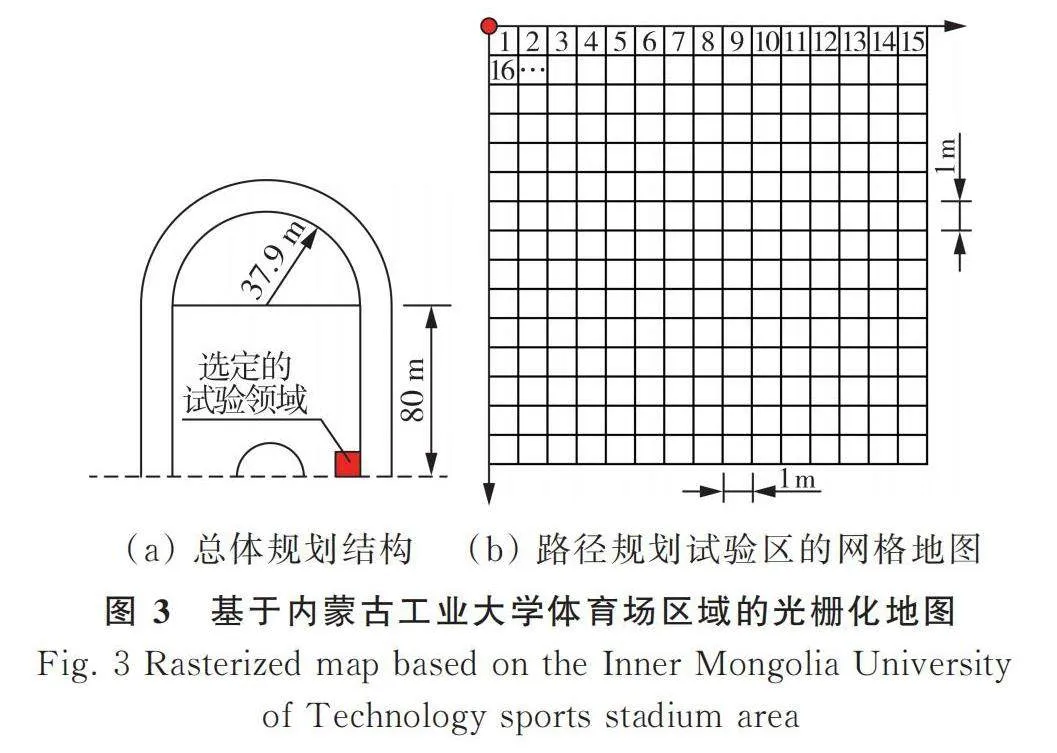
路徑規劃工作離不開地圖搭建，考慮到試驗場地的可獲取性以及地形相似性，本文選定的試驗區域為內蒙古工業大學的體育場。因為體育場和多數牧場一樣，均為平面地形，且都具有因為草本植物或人造填充物帶來的地表摩擦環境。在生成抽象地圖或環境模型之前，需要設置一些規則。首先兩個障礙物之間的間距小于機器人的通行距離，這兩個障礙物應該被當作一個障礙物。其次對機器人進行路徑規劃研究時，為方便計算，將機器人看為質點，選用實用且規劃結果查看簡單的柵格法構建地圖。考慮到學校體育場的日常運營需求、試驗的計算量、場地條件，從內蒙古工業大學體育場中選取15 m×15 m的正方形區域構建試驗地圖。柵格法將選定的試驗場地劃分為多個邊長為1 m的正方形，便于確定障礙物的位置和大小信息。柵格地圖中的所有柵格編號方式分為序號標識法與直角坐標法，前者即從研究場地左上角的柵格開始，依次按照從左到右、從上到下的順序編號。設柵格直角坐標法編號中，以從左到右、從上到下順序作為水平軸、垂直軸的正方形，將整個柵格地圖左上角作為原點。構建出的試驗地圖見圖3。

直角坐標法與序號標識法的轉換方法如式（11）、式（12）所示。

[n=15y+x+1] （11）

式中： n——序列號變量；

（x，y）——柵格所處的坐標。

[x=mod（n，15）-1y=int（n/15）] （12）

考慮到此次研究選取的試驗區域較大，柵格較多，選用序號更加簡潔的序號標識法更為合適。再對組成路徑規劃模型的GA算法模塊進行設計。GA算法是一種成熟的智能優化算法，這里僅對其中需要特別關注的要點進行設計。選用式（13）來判斷插入柵格后兩柵格是否符合連續條件。

[D=maxabs（xi+1-xi），abs（yi+1-yi）] （13）

式中： xi、yi——柵格Ni在直角坐標系的坐標值；

xi+1、yi+1——Ni+1的坐標值；

D——柵格連續判斷變量。

如果式（13）中D為1，代表兩柵格是連續的，反之則說明兩者不連續，需要使用中值法插入柵格，如式（14）所示。

[xi'=int（xi+xi+1）/2yi'=int（yi+yi+1）/2Ni'=xi'+n12yi'+1] （14）

式中： [Ni']——按中值法計算出的插入柵格；

[xi']、[yi']——該柵格的對應坐標。

其次此次研究的問題為路徑規劃類型，將路徑長度作為評價路徑方案好壞的指標較為合適。因此設計出如式（15）所示的適應度函數[19]。

[L=1+1Ud（gi，gi+1）] （15）

式中： U——路徑段總數量；

d（gi，gi+1）——相鄰兩柵格之間的距離。

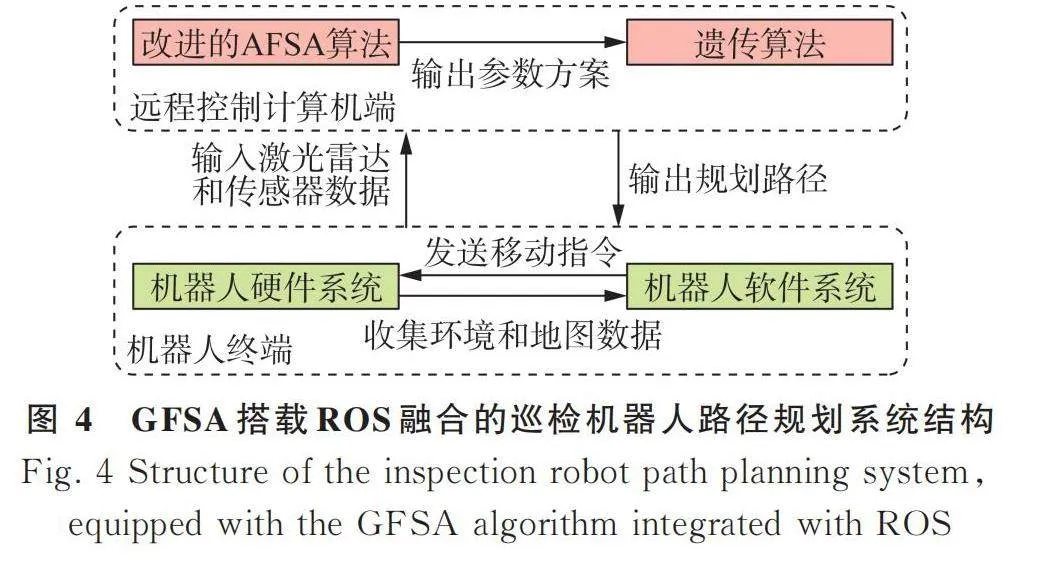
至此本文將GFSA搭載到ROS融合的巡檢機器人路徑規劃系統設計完成，其整體運行結構如圖4所示。

3 路徑規劃試驗與分析

為測試本文設計的牧場巡檢機器人系統的使用性能，設計并開展一項路徑規劃試驗。試驗中路徑規劃的地圖為內蒙古工業大學體育場中選出的15 m×15 m的正方形區域。

3.1 GFSA性能對比結果分析

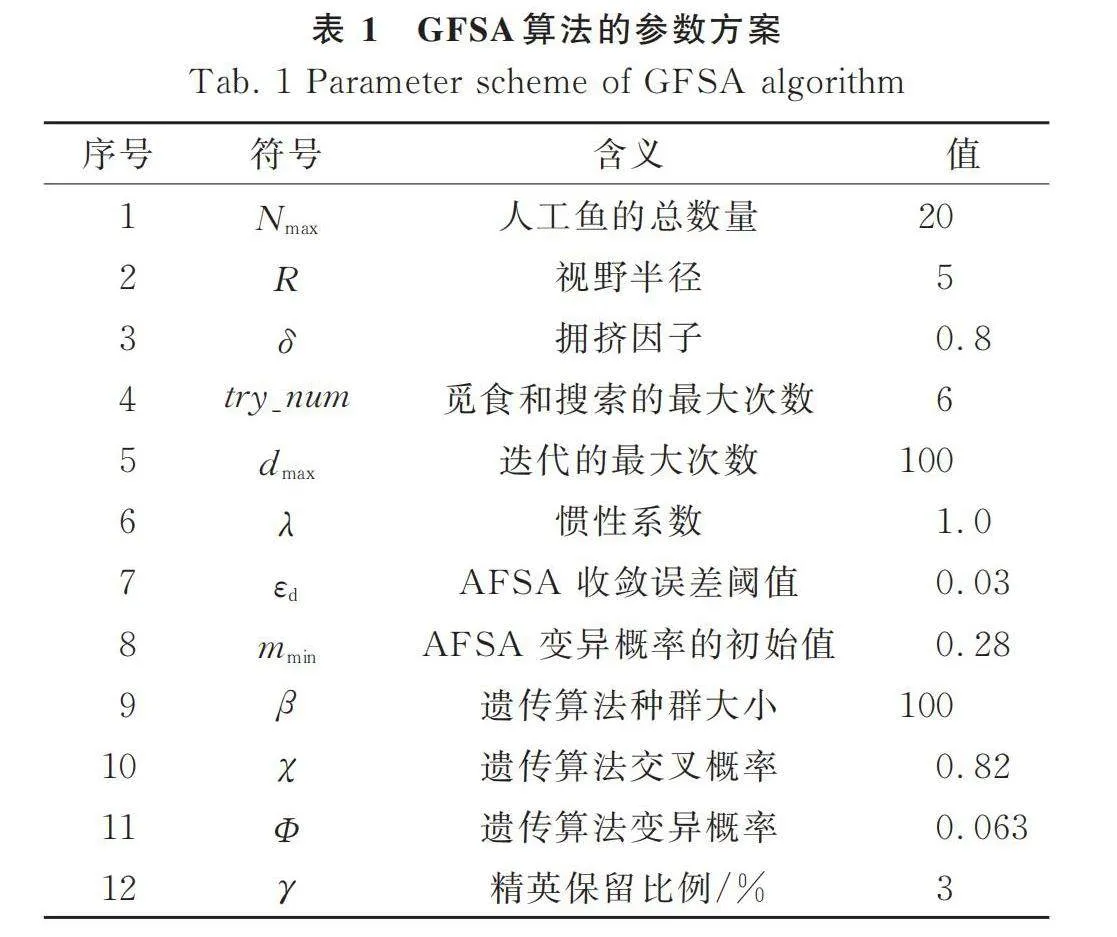
試驗共分為兩部分，第一部分是消融試驗，目的是驗證此次設計的GFSA在路徑規劃任務處理上的效果。第二部分是對比試驗，目的是對比分析此次設計的GFSA與其余不同類型的常用路徑規劃算法在規劃性能上的區別。消融試驗中選擇的所有算法方案分別有傳統的GA、傳統的AFSA、使用改進AFSA優化GA初始種群的算法（以下簡稱AFSA+GA）、AFSA+GA中僅添加可變視野與步長改進的算法（以下簡稱AFSA1+GA）、AFSA+GA中僅添加擁擠因子改進的算法（以下簡稱AFSA2+GA）、AFSA+GA中僅添加改進變異方法的算法（以下簡稱AFSA3+GA）以及包含以上三種改進的方案（以下簡稱GFSA）。對比試驗中選取的對比算法A-star算法（A*）、粒子群算法（Particle Swarm Optimization， PSO）、快速擴展隨機樹算法（Rapidly exploring random tree， RRT）。試驗中涉及的全部算法參數均通過在常見設置范圍內，按二分法多次試運行取最優方案的方式取得。試運行得到此次研究設計的GFSA方案的參數見表1。

試驗開始后，試驗區域將按照障礙物占比或稱障礙率，隨機擺放障礙物，用以模擬牧場巡檢機器人在使用中可能遇到的巖石、植物等障礙。每次試驗的路徑規劃起點與終點均為試驗區域的左上角第一個柵格與右下角最后一個柵格。

3.2 路徑規劃效果試驗分析

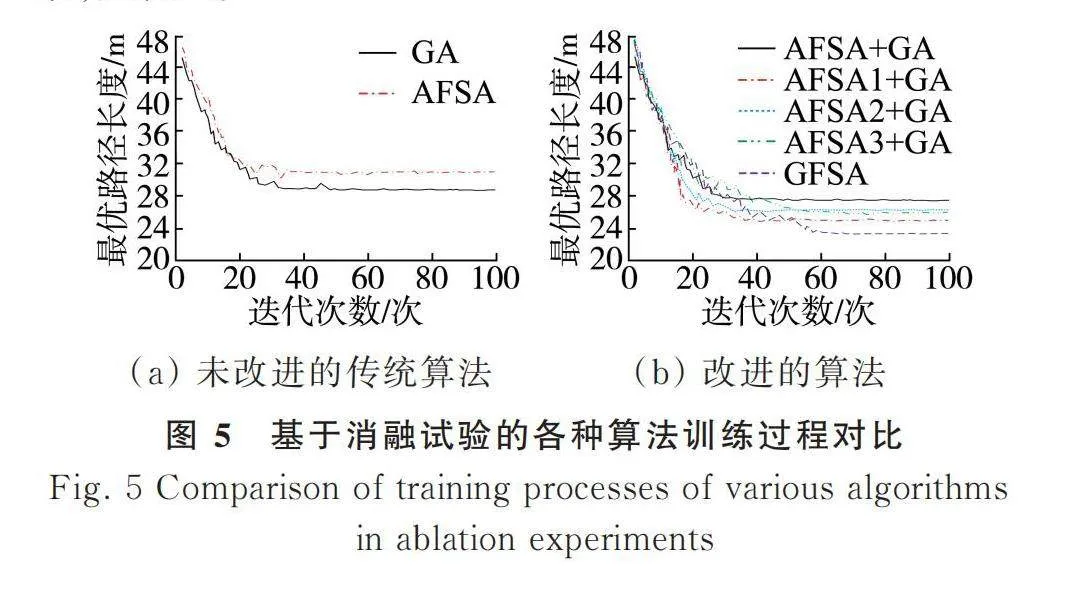
消融試驗后得到不同算法方案的訓練過程統計結果，見圖5。

由圖5可知，訓練開始后，各算法的最優路徑長度不斷減小并趨于穩定，而GFSA方案收斂后的最優路徑長度最短。當迭代次數達到100次時，GA、AFSA、AFSA+GA、AFSA1+GA、AFSA2+GA、AFSA3+GA、GFSA的最優路徑長度分別為31.7 m、29.8 m、27.6 m、25.0 m、26.3 m、26.1 m、23.7 m。

對比各算法方案的規劃路線，如圖6所示。考慮到算法每次運行的結果不一致，因此每種算法均重復運行50次。由圖6可知，GA、AFSA、AFSA+GA、AFSA1+GA、AFSA2+GA、AFSA3+GA、GFSA的最優路徑長度中位數分別為29.9 m、29.6 m、27.3 m、26.3 m、26.2 m、26.5 m、23.2 m。

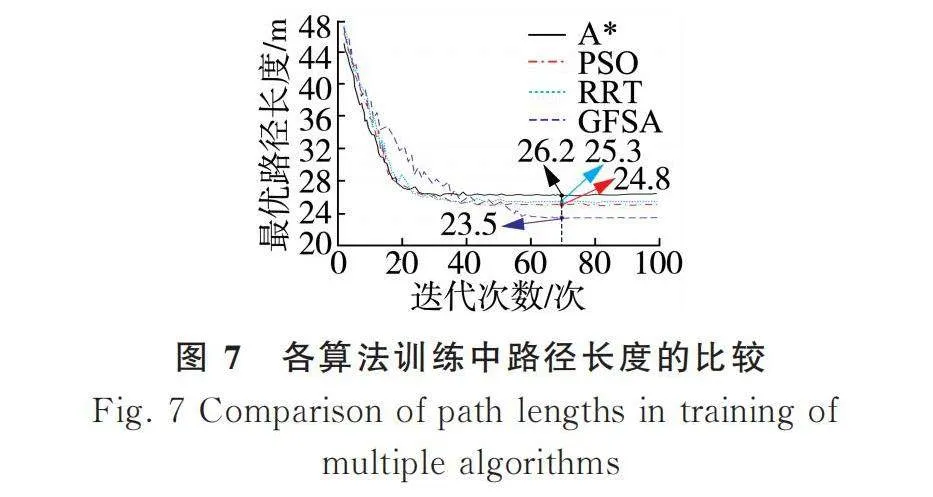
從圖5和圖6的分析結果可知，結合了可變視野與步長、擁擠因子改進、變異方法的GFSA規劃出的路線最短，在這種巡檢方式下，機器人的巡檢效率最高，因此后續試驗均選擇GFSA與其余類型算法對比。使用GFSA開展多算法對比試驗，得到它們在訓練過程中的最優路徑長度與平均路徑長度數據，如圖7所示。

由圖7可知，與圖5類似的是，隨著迭代次數的增長，各算法最優路徑長度仍然呈現先減小后收斂的變化規律，說明算法訓練正常。A*收斂速度最快，在迭代24次后，即完成訓練。當迭代次數達到70次后，認為各模型均完成訓練，這時A*、PSO、RRT、GFSA的最優路徑長度分別為26.2 m、24.8 m、25.3 m、23.5 m。再從優化后的具體路徑角度定性分析各算法，隨機選出一次測試結果的柵格地圖，如圖8所示。

由圖8可知，此次研究設計的GFSA規劃的路徑總長度最小，且整體轉彎幅度也明顯小于其余算法，可以減少由于大幅度轉彎帶來的減速效果，從而有利于減少設備的使用損耗和故障，提高牧場巡檢機器人的巡檢效率。

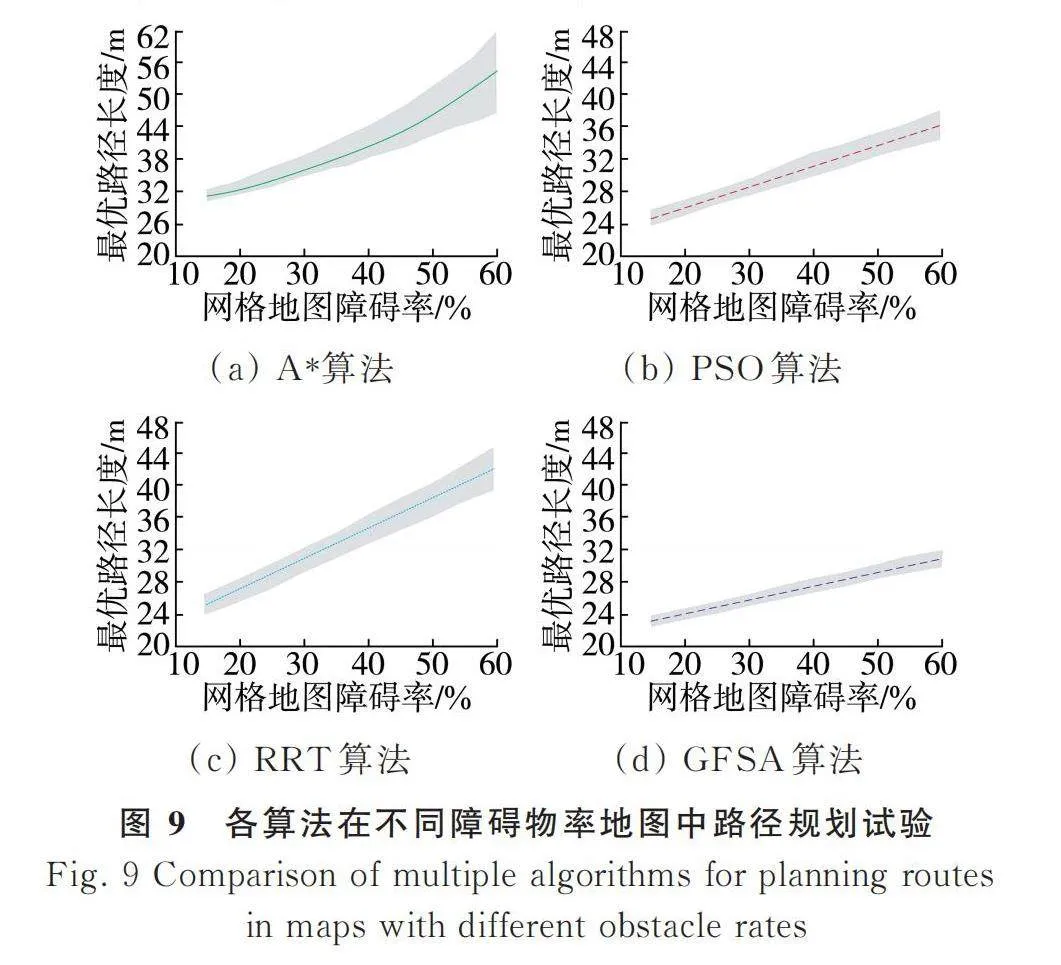
試驗均為在貼近牧場實際地形狀態的障礙率條件下取得，為驗證算法在不同復雜地形條件下的路徑規劃能力，再調整地圖中的障礙率多次試驗，統計結果見圖9。

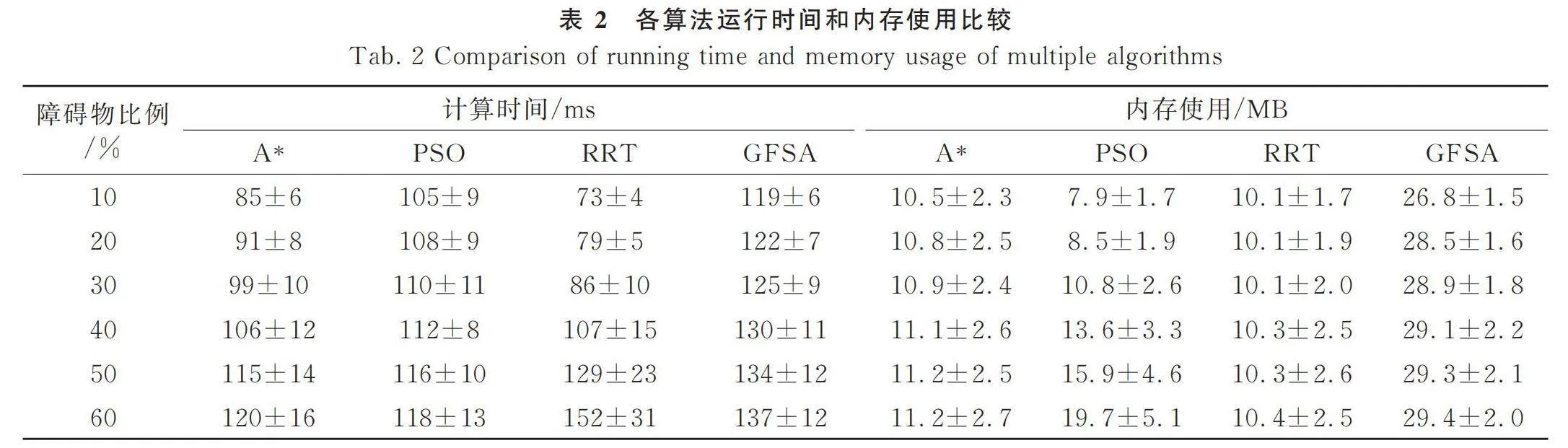
為提升統計精度，每種試驗方案重復運行5次。圖9中灰色區域為對應算法規劃的最優路徑長度最大值與最小值組成的，各線條為五次平行試驗最優路徑的均值繪制而成。由圖9可知，隨著地圖障礙率增長，A*最優路徑長度出現加速增長變化趨勢，且規劃結果的極值波動范圍也在增長。其余三種算法最優路徑長度隨地圖障礙率增長呈現的是線性變化規律。且GFSA的最優路徑長度初始值、增長斜率均小于對比算法。說明GFSA的魯棒性和適應性較好。最后對比各算法在不同地圖障礙率條件下的運行耗時與占用內存，數據按照“均值±標準差”形式展示，統計結果見表2。

由表2可知，A*與RRT在各種障礙率下的計算耗時與占用內存均較低，這主要是因為這兩種算法的計算復雜度較低。而GFSA的計算耗時與占用內存高于對比模型。例如在障礙率為50%條件下，A*、PSO、RRT、GFSA的計算耗時與占用內存均值分別為115 ms、116 ms、129 ms、134 ms與11.2 MB、15.9 MB、10.3 MB、29.3 MB。

4 結論

為提高牧場巡檢機器人的路徑規劃效果，針對AFSA算法在牧場巡檢路徑規劃的過程中易陷入局部最優解、規劃的最優路徑較長等問題，提出一種改進AFSA算法融合GA算法得到的GFSA算法，將所提算法搭載到牧場巡檢機器人上進行試驗。

1） 在消融試驗中，GFSA算法能夠顯著降低路徑規劃的最優路徑長度。試驗過程中使用不同的優化方法對算法性能的提升有所差異，其中使用結合可變視野與步長、擁擠因子改進、變異方法的GFSA規劃出的路線最短，其最優路徑長度中位數為23.2 m。采用其他改進方法的算法最優路徑長度中位數均有所增加，其中傳統AFSA和GA算法路徑規劃的效果最差。

2） 在對比試驗中，與其他算法相比，GFSA算法在路徑規劃方面表現出更優異的效果，規劃出的路徑整體轉彎幅度顯著較小，有助于降低由于大幅度轉彎引起的速度減緩效應，從而有利于減少設備的使用損耗和故障風險，提高牧場巡檢機器人的運行效率。

3） 鑒于牧場復雜環境和牲畜活動等因素可能對路徑規劃精度造成影響，在接近牧場實際地形狀態的障礙率條件下，通過調整地圖中的障礙率來考察不同算法的適應性。隨著地圖障礙率增加，GFSA算法的增長斜率均小于對比算法，表明GFSA算法具有良好的魯棒性和適應性。

設計的GFSA算法規劃出的路徑最短且路線轉彎幅度小，有利于減少設備的損耗，提高牧場巡檢的效率。其缺點在于GFSA算法計算耗時長，內存占用高，對硬件要求較高。為改進此問題，后續研究可以考慮對算法進行優化，如采用算法參數優化、優化算法結構、并行化計算等方式，在保證牧場環境下路徑規劃準確可靠的同時，盡可能地減少算法的計算耗時和內存占用。

參 考 文 獻

[ 1 ] Ma Y， Feng W， Mao Z， et al. Path planning of UUV based on HQPSO algorithm with considering the navigation error [J]. Ocean Engineering， 2022， 244： 110048.

[ 2 ] 王杰， 經俊森， 陳正偉， 等. 基于Harris和卡爾曼濾波的農業機器人田間穩像算法[J]. 農業機械學報， 2023， 54（1）： 30-36， 53.

Wang Jie， Jing Junsen， Chen Zhengwei， et al. Field image stabilization algorithm for agricultural robot based on Harris and Kalman filter [J]. Transactions of the Chinese Society for Agricultural Machinery， 2023， 54（1）： 30-36， 53.

[ 3 ] Yi H， Wang J， Hu Y， et al. Mechanism isomorphism identification based on artificial fish swarm algorithm [J]. Proceedings of the Institution of Mechanical Engineers， Part C： Journal of Mechanical Engineering Science， 2021， 235（21）： 5421-5433.

[ 4 ] Merci A， Anthierens C， Thirion?Moreau N， et al. A simulator of underwater glider missions for path planning [J]. Ocean Engineering， 2023， 269： 113514.

[ 5 ] 常見， 任雁. 基于改進遺傳算法的機器人路徑規劃[J]. 組合機床與自動化加工技術， 2023（2）： 23-27.

Chang Jian， Ren Yan. Robot path planning based on improved genetic algorithm [J]. Modular Machine Tool & Automatic Manufacturing Technique， 2023（2）： 23-27.

[ 6 ] 高明， 唐洪， 張鵬. 機器人集群路徑規劃技術研究現狀[J]. 國防科技大學學報， 2021， 43（1）： 127-138.

Gao Ming， Tang Hong， Zhang Peng. Survey of path planning technologies for robots swarm [J]. Journal of National University of Defense Technology， 2021， 43（1）： 127-138.

[ 7 ] Tian Q， Wang T， Wang Y， et al. A two?level optimization algorithm for path planning of bionic robotic fish in the three?dimensional environment with ocean currents and moving obstacles [J]. Ocean Engineering， 2022， 266： 112829.

[ 8 ] Zhang Y， Chen P， Chen L， et al. A path planning method for the autonomous ship in restricted bridge area based on anisotropic fast marching algorithm [J]. Ocean Engineering， 2023， 269： 113546.

[ 9 ] Xue H. A quasi?reflection based SC-PSO for ship path planning with grounding avoidance [J]. Ocean Engineering， 2022， 247： 110772.

[10] Yan Z， Zhang J， Zeng J， et al. Three?dimensional path planning for autonomous underwater vehicles based on a whale optimization algorithm [J]. Ocean Engineering， 2022， 250： 111070.

[11] Zhang L， Zhang Y， Li Y. Mobile robot path planning based on improved localized particle swarm optimization [J]. IEEE Sensors Journal， 2020， 21（5）： 6962-6972.

[12] Zhao L， Wang F， Bai Y. Route planning for autonomous vessels based on improved artificial fish swarm algorithm [J]. Ships and Offshore Structures， 2023， 18（6）： 897-906.

[13] Li S， Li W， Wang Z， et al. Research and implementation of parallel artificial fish swarm algorithm based on ternary optical computer [J]. Mobile Networks and Applications， 2022， 27（4）： 1397-1407.

[14] 金秀章， 于靜， 劉岳. 基于人工魚群-徑向基神經網絡的NOx預測模型[J]. 動力工程學報， 2021， 41（7）： 551-557.

Jin Xiuzhang， Yu Jing， Liu Yue. NOx prediction model based on artificial fish swarm?radical basis function neural network [J]. Journal of Chinese Society of Power Engineering， 2021， 41（7）： 551-557.

[15] 靳荔成， 劉一萱， 白瑞峰， 等. 面向校園多機器人協同巡查的路徑規劃虛擬仿真試驗設計[J]. 試驗技術與管理， 2023， 40（3）： 93-99.

Jin Licheng， Liu Yixuan， Bai Ruifeng， et al. Design of virtual simulation experiment of path planning for multi?robot cooperative patrol in campus [J]. Experimental Technology and Management， 2023， 40（3）： 93-99.

[16] 畢桂. 染色體重組魚群算法的機器人導航路徑規劃[J]. 機械設計與制造， 2021（6）： 197-201.

Bi Gui. Robot navigation path planning based on chromosome recombination fish swarm algorithm [J]. Machinery Design & Manufacture， 2021（6）： 197-201.

[17] Zhao L， Bai Y， Wang F， et al. Path planning for autonomous surface vessels based on improved artificial fish swarm algorithm： A further study [J]. Ships and Offshore Structures， 2023， 18（9）： 1325-1337.

[18] Lyridis D V. An improved ant colony optimization algorithm for unmanned surface vehicle local path planning with multi?modality constraints [J]. Ocean Engineering， 2021， 241： 109890.

[19] Xi L， Zhang F. An adaptive artificial?fish?swarm?inspired fuzzy C-means algorithm [J]. Neural Computing and Applications， 2020， 32（22）： 16891-16899.