一種基于幅度相位信息輔助的多假設跟蹤算法

摘 要： 傳統多目標跟蹤算法在距離拖引（Range Gate Pull Off， RGPO）干擾場景中， 由于無法有效區分真實目標和干擾， 將出現目標航跡起始錯誤、 跟蹤誤差增大、 跟蹤中斷等現象， 嚴重影響跟蹤性能。 針對這一問題， 基于雷達量測的幅度和相位特征提出一種信息輔助多假設跟蹤（Information Assisted Multiple Hypothesis Tracking， IA-MHT）算法。 IA-MHT算法利用了幅度、 相位信息區分目標真實量測和虛假量測， 并基于判別結果修正了全局聯合假設概率和航跡得分的計算步驟， 從而提高算法的抗雜波和抗干擾性能。 在RGPO干擾場景中的仿真結果表明， IA-MHT算法能夠有效區分干擾量測， 獲得優于傳統MHT算法的數據關聯性能。

關鍵詞： 多假設跟蹤； 距離拖引干擾； 信息輔助； 航跡得分

中圖分類號： TJ760

文獻標識碼： A

文章編號： 1673-5048（2024）05-0088-08

DOI： 10.12132/ISSN.1673-5048.2024.0078

0 引 言

雷達干擾技術種類繁多， 根據干擾能量來源不同可以分為有源干擾和無源干擾； 根據干擾效果不同可以分為壓制干擾和欺騙干擾［1］。 距離拖引（Range Gate Pull Off， RGPO）干擾是一類簡單高效的距離欺騙雷達干擾技術， 通過產生與真實目標徑向距離不同的虛假目標， 干擾敵方雷達對真實目標的跟蹤。 干擾機在產生RGPO干擾時， 通常使用數字射頻存儲（Digital Radio Frequency Memory， DRFM）技術生成與真實目標回波信號在頻率、 波形和電磁散射特性等方面高度相似的虛假目標信號， 并通過不斷調整虛假目標信號的時間延遲影響雷達對目標真實距離的測量， 從而實現干擾雷達跟蹤的目的［2-3］。 RGPO干擾可以有效擾亂雷達跟蹤系統對目標的探測和航跡起始過程， 導致目標航跡起始錯誤、 跟蹤誤差增大、 跟蹤中斷等問題。

盡管目前已有較多針對單目標的抗RGPO干擾跟蹤算法， 但這類算法通常不適用于多目標與多干擾場景［4-5］。 為了解決RGPO干擾環境下的多目標跟蹤問題， 文獻［6］通過高信噪比量測之間的角度差判別RGPO干擾， 并利用多假設跟蹤（Multiple Hypothesis Tracking， MHT）算法獲得真實目標和RGPO干擾的航跡。 然而該算法在雜波密集、 干擾數量較多的場景下性能表現欠佳。 文獻［7］利用回波信號的幅度特征改進基數概率假設密度（Cardinalized Probability Hypothesis Density， CPHD）濾波器的似然概率計算方法， 提高了算法在干擾環境下的勢估計準確度。 然而CPHD算法無法直接提供目標航跡序號， 在實際應用中存在不便。 文獻［8］提出一種利用稀疏分解系數和雙譜特征區分目標和RGPO干擾的MHT算法， 獲得了良好的跟蹤性能。 然而使用神經網絡融合特征也導致該算法計算復雜度較高。

上述抗RGPO干擾多目標跟蹤算法在跟蹤性能、 應用便利程度等方面仍存在不足。 針對RGPO干擾環境下的多目標跟蹤問題， 本文提出一種基于幅度和相位信息輔助的多假設跟蹤算法。 該算法利用雷達信號的幅度和相位信息實現目標真實量測和干擾量測的區分， 改進了傳統MHT算法的數據關聯和航跡得分計算方法， 從而提高MHT算法的抗雜波、 抗干擾能力， 使雷達目標跟蹤系

統在RGPO干擾環境下獲得更高的跟蹤精度和穩定性。

1 問題描述

在典型的RGPO干擾場景中， 真實目標、 雜波和

收稿日期： 2024-05-11

*作者簡介： 郭玉霞（1979-）， 女， 河南滑縣人， 研究員。

RGPO干擾量測在空間中的分布如圖1所示。 其中， 干擾量測與真實目標量測的方位角基本一致， 但徑向距離不同。 本文所研究的問題可以描述為在RGPO干擾場景中， 基于MHT算法框架和量測輔助信息實現對多個機動目標的準確跟蹤。

1.1 TOMHT算法

航空兵器 2024年第31卷第5期

郭玉霞， 等： 一種基于幅度相位信息輔助的多假設跟蹤算法

MHT是一種通過計算量測序列源自不同目標的概率， 從而基于延遲決策進行數據關聯的多目標跟蹤算法。 根據實現方式的不同， MHT算法可分為面向假設的MHT（Hypothesis-Orientated MHT， HOMHT）［9-10］和面向航跡的MHT（Track-Orientated MHT， TOMHT）兩類［11］。 其中， HOMHT算法采用“自頂向下”的設計思路， 直接通過計算量測-目標全局聯合關聯假設的概率求出最優假設； 而TOMHT算法采用“自底向上”的結構， 首先產生可能的量測-航跡關聯假設， 再利用似然概率計算航跡得分， 最后利用多維分配算法求出最優的全局聯合關聯假設。 TOMHT算法因計算資源消耗少、 實現較為簡單、 可直接獲得航跡等優點獲得更廣泛的應用。

航跡得分的計算是TOMHT算法的核心步驟。 令Θk， l表示k時刻的第l個聯合關聯假設， Zk={Z（1）， Z（2）， …， Z（k）}表示由初始時刻累積至k時刻的量測集合， 則可以使用貝葉斯公式計算k時刻全局聯合假設的概率。

P{Θk， l|Zk}=1cP{Z（k）|θ（k）， Θk－1， s， Zk－1}·

P{θ（k）|Θk－1， s， Zk－1}P{Θk－1， s|Zk－1}（1）

式中： Θk－1， s為Θk， l的父聯合關聯假設； k時刻量測集合Z（k）的關聯假設記作θ（k）； c為歸一化常數。 TOHMT算法通常使用對數似然比（LLR）將式（1）中的累乘簡化為累加運算獲得航跡得分； 再經過航跡分簇、 最優分配等步驟進行數據關聯； 最終通過航跡樹剪枝、 航跡更新等步驟輸出跟蹤結果［12］。 TOMHT算法的完整流程如圖2所示。

1.2 雷達量測的幅度和相位信息

傳統多目標跟蹤算法由于僅使用了雷達量測的位置信息， 無法在RGPO干擾場景中有效地區分目標真實量測和干擾， 導致算法的關聯準確度降低、 虛假航跡數量增多、 航跡維持性能下降。 為解決上述問題， 本文使用雷達量測的幅度和相位信息進行似然比檢驗以輔助判別量測的來源， 一方面減小干擾和雜波對TOMHT算法關聯性能的影響， 另一方面降低算法后續步驟的計算復雜度。

已有研究表明， 窄帶雷達量測中包含的幅度信息可以使用瑞利分布模型描述［13］， 具體模型描述如下： 假定生成量測時信號（包絡）幅度為q， 并對雜波（含噪聲）進行歸一化處理， 則對于目標不存在的H0假設， 雜波所產生虛假量測幅度q的概率密度函數為

p0（q）=qexp－q22， q≥0 （2）

對于目標存在的H1假設， 量測幅度q的概率密度函數為

p1（q）=q1+dexp－q22（1+d）， q≥0 （3）

式中： d為目標信噪比期望值。 將參數d視為先驗信息， 則利用幅度信息判斷量測源于目標或雜波的似然比檢驗表示為

Λ（q）=lgp1（q）p0（q）=－lg（1+d）+dq22（1+d）H1H0η1 （4）

在實際應用中， 由于回波信號的期望功率會隨著目標姿態角的變化而發生改變， 信噪比參數1+d的準確數值是難以獲取的。 假定d（以dB為單位）在區間［d1， d2］中均勻分布， 可以推導出目標量測幅度的似然函數為［14］

p1（q）=2exp－q22（1+d2）－exp－q22（1+d1）q［lg（1+d2）－lg（1+d1）］， q≥0（5）

在似然比檢驗中使用式（5）代替式（3）， 可以降低參數d設置錯誤對判斷結果造成的不利影響。

利用量測幅度信息可以輔助TOMHT算法排除雜波干擾， 提高數據關聯的準確性。 然而當目標釋放RGPO干擾時， 干擾量測的幅度特征很可能與真實量測高度相似， 使得基于幅度信息似然比檢驗的判別方法失效。 為了提高TOMHT算法對抗RGPO干擾的能力， 需要利用干擾信號和真實目標信號之間的相位特征差異識別干擾量測， 提高關聯正確率并減少虛假航跡數量。

現代雷達干擾系統多采用DRFM作為核心組件， DRFM的主要功能是將接收到的射頻信號數字化， 以便存儲、 處理、 重建射頻信號， 最終產生干擾對方跟蹤雷達所需的信號［15］。 常見的距離拖引、 速度拖引等干擾形式均可以通過DRFM系統實現［16］。 由于DRFM對模擬信號進行了數字化處理， 其采樣數、 量化位數等參數會影響射頻信號的重建準確度， 這一特性使得利用DRFM信號與目標真實信號之間的相位差異區分目標和干擾量測成為可能。 文獻［17］定義了干擾誤差角度μ， 用于評估DRFM所產生的干擾信號和真實信號之間的差異。 若目標信號和干擾信號在一個雷達脈沖重復周期的采樣序列分別為x=［x（0）， x（1）， …， x（K－1）］T， y=［y（0）， y（1）， …， y（K－1）］T， 其中：

x（n）=ej2πfDn（6）

y（n）=∑1/2Nf0」m=－1/2Nf0」sincm+1Nej（Nm+1）2πf0n（7）

cosμ=cos（x， y）=|xHy|‖x‖·‖y‖（8）

式中： μ為干擾誤差角； fD表示目標的歸一化多普勒頻率； f0為DRFM歸一化頻率； K表示雷達在一個脈沖重復周期內的信號采樣次數； N=2M， M表示量化位數。

由于干擾信號向量通常無法直接獲得， 可以使用量測信號計算干擾誤差角［17］。 將量測信號向量表示為z=［z（0）， z（1）， …， z（K－1）］T， 則有二元檢驗模型：

H1： z=n+αp

H2： z=n+βpjam （9）

式中： H1表示信號來自目標， H2表示信號來自干擾源； n～CN（0， M）為復高斯噪聲向量； α～CN（0， σ2α）， β～CN（0， σ2β）為復高斯隨機變量； 基于目標信號采樣可構建目標的導向矢量為p=［ej2πfD×0， …， ej2πfD×（K－1）］T； 干擾信號的未知導向矢量為pjam。 則代入式（8）可得干擾誤差角的表達式為

μ=arccospHM－1z（pHM－1p）（zHM－1z） （10）

基于上述討論可知， 根據DRFM量化位數、 采樣次數等先驗信息適當設定門限， 能夠利用干擾誤差角μ實現對RGPO干擾量測的判別。 可通過自適應相干檢測器（Adaptive Coherent Estimator， ACE）設置干擾誤差角檢測門限［18］。

2 信息輔助多假設跟蹤

為了改善傳統TOMHT算法在RGPO干擾下的性能表現， 本文首先利用雷達量測的幅度、 相位信息輔助區分目標、 干擾和雜波量測， 提高量測來源判別的準確性； 再根據判別結果對航跡得分的計算步驟進行調整， 從而分離目標和RGPO干擾的數據關聯過程； 最終建立基于信息輔助的抗干擾多假設跟蹤（Information Assisted MHT， IA-MHT）算法。 以下重點對航跡得分的計算過程進行說明。

輸入IA-MHT算法的量測Z（k）包含位置信息Zp（k）和幅度信息Za（k）， 因此可以將全局假設概率式（1）中等號右側的第一項進一步分解為

P{Z（k）|θ（k）， Θk－1， s， Zk－1}=

P{Zp（k）|θ（k）， Θk－1， s， Zk－1}·

P{Za（k）|θ（k）， Θk－1， s， Zk－1}（11）

對于被判別為來自雜波的量測， 幅度似然函數P（Za（k）|θ（k）， Θk－1， s， Zk－1）可使用式（2）計算； 對于被判別為來自目標或干擾的量測， 似然函數可使用式（5）計算。 由于量測之間相互獨立， 位置量測的似然函數可以分解為累乘形式：

P{Zp（k）|θ（k）， Θk－1， s， Zk－1}=

∏m（k）j=1{fj［zj（k）|Θk－1， s， Zk－1］} （12）

假定虛警、 新目標和新干擾在量測空間中均勻分布， 并且濾波模型服從高斯假設， 則有

fj［zj（k）|Θk－1， s， Zk－1］=

1/V， 量測由虛警或新目標、 新干擾產生

N（zj（k）－z^t（k）， St）， 量測來自已確認目標

N（zj（k）－z^f（k）， Sf）， 量測來自已確認干擾 （13）

式中： V表示量測空間體積； z^（k）為位置量測的預測均值； S為新息協方差矩陣。

在k時刻， 關聯假設θ（k）對共計m（k）個量測進行分配， 如表1所示。 則θ（k）的先驗概率可分解為兩部分：

P{θ（k）|Θk－1， s， Zk－1}=P{θ（k）|τ， ， ν， ξ， ψ， Θk－1， s， Zk－1}=P{θ（k）|τ， ， ν， ξ， ψ}·P{τ， ， ν， ξ， ψ}（14）

假定各個關聯假設的先驗概率相等， 則有

P{θ（k）|τ， ， ν， ξ， ψ}=

［Pm（k）τ+ξ·C+ν+ψν·C+ψψ］－1=

m（k）！（m（k）－τ－ξ）！ （+ν+ψ）！ν！（+ψ）！ （+ψ）！ψ！！－1=

！ν！ψ！m（k）！ （15）

P{τ， ， ν， ξ， ψ} =∏t{［PDt （k）］δt［1-PDt（k）］1-δt}·

∏f{［PDf（k）］δf［1-PDf（k）］1-δf}·

p（）pν（ν）pψ（ψ）（16）

式中： 變量δt和δf用于指示當前時刻雷達是否探測到某條航跡。

δt=0， 若沒有量測與目標航跡t相關聯

1， 若有量測與目標航跡t相關聯 （17）

δf=0， 若沒有量測與干擾航跡f相關聯

1， 若有量測與干擾航跡f相關聯 （18）

將式（11）～（16）代入式（1）， 可得到全局關聯假設概率的表達式：

P{Θk， l|Zk}=1c ！ν！ψ！m（k）！p（）pν（ν）pψ（ψ）·

∏m（k）j=1{ftj［zj（k）|Θk－1， s， Zk－1］}·

∏t{［PDt（k）］δt［1－PDt（k）］1－δt}·

∏f{［PDf（k）］δf［1－PDf（k）］1－δf}·

P{Θk－1， s|Zk－1}（19）

假定雜波信號數量、 新目標數量ν和新干擾數量ψ均服從泊松分布， 即有概率密度函數：

p（）=e－λV（λV）！（20）

pν（ν）=e－λνV（λνV）νν！（21）

pψ（ψ）=e－λψV（λψV）νψ！（22）

式中： λ表示虛警空間密度； V表示監視區域大小； λν表示新目標空間密度； λψ表示新干擾空間密度。 假定虛警、 新目標和新干擾在區域內均勻分布， 即概率密度函數為1/V， 將式（20）～（22）代入式（19）， 可得到全局關聯假設概率計算式：

P{Θk， l|Zk}=1c e－λVe－λνVe－λψVm（k）！（λ）（λν）ν（λψ）ψ

∏m（k）j=1{fj［zj（k）|Θk－1， s， Zk－1］}τj·

∏t{［PDt（k）］δt［1－PDt（k）］1－δt}

∏f{［PDf（k）］δf［1－PDf（k）］1－δf}P{Θk－1， s|Zk－1}=

1c′（λ）（λν）ν（λψ）ψ∏m（k）j=1{fj［zj（k）|Θk－1， s， Zk－1］}τj∏t{［PDt（k）］δt［1－PDt（k）］1－δt}·

∏f{［PDf（k）］δf［1－PDf（k）］1－δf}P{Θk－1， s|Zk－1}

（23）

在TOMHT算法中， 通常使用對數似然比計算航跡得分， 進而確定最佳的全局假設［19］。 以下推導IA-MHT算法中LLR航跡得分的計算公式， 令指示向量為τ=［τ1， τ2， …， τm（k）］， 其中：

τj=0， 若量測由虛警或新目標、 新干擾產生

1， 若量測來自已確認的目標或干擾 （24）

則有

（λ）m（k）=（λ）+ν+ψ+∑m（k）j=1τj（25）

將式（23）等號右側部分除以（λ）m（k）， 再將（λ）－m（k）并入常數c中使等式保持成立， 可以得到：

P{Θk， l|Zk}=

1cλνλνλψλψ∏m（k）j=1fj［zj（k）|Θk－1， s， Zk－1］λτj·

∏t{［PDt（k）］δt［1－PDt（k）］1－δt}·

∏f{［PDf（k）］δf［1－PDf（k）］1－δf}P{Θk－1， s|Zk－1}（26）

由式（26）可推導得到新目標的似然比為

lν/=λνλ（27）

同理， 新干擾的似然比為

lψ/=λψλ（28）

目標軌跡連續（當前時刻有量測與軌跡關聯）的似然比為

ltj=fj［zj（k）|Θk－1， s， Zk－1］λPDt（k）（29）

目標軌跡中斷的似然比為

lt0=1－PDt（k）（30）

同理， 干擾軌跡連續的似然比為

lfj=fj［zj（k）|Θk－1， s， Zk－1］λPDf（k）（31）

干擾軌跡中斷的似然比為

lf0=1－PDf（k）（32）

在IA-MHT算法中， 將上述似然比取對數， 累加計算LLR航跡得分

1（k）=1（k－1）+Δ1（k）=1（k－1）+lnl（33）

再利用序貫概率比檢驗（Sequential Probability Ratio Test， SPRT）進行航跡管理， 減少虛假航跡的數量［20］； 最后利用匈牙利算法求出最優的全局關聯假設， 并基于航跡全局概率進行剪枝， 降低算法計算量。 需要注意真實目標和干擾目標的關聯過程是相互獨立的， 即僅有被判別為目標的量測會與目標航跡相關聯， 僅有被判別為干擾的量測會與干擾航跡相關聯。

3 仿真實驗與分析

在典型RGPO干擾場景參數下進行機動目標跟蹤仿真實驗， 基于最優子模式分配距離（Optimal Sub-Pattern Assignment， OSPA）、 勢估計、 數據關聯正確率、 關聯錯誤率、 航跡零碎度等性能評價指標［21］， 對比傳統TOMHT算法和本文所提出的IA-MHT算法的性能表現。 在某一時刻， 對于目標實際位置集合X={x1， …， xm}和跟蹤算法所估計的目標位置集合Y={y1， …， yn}， OSPA距離定義為

d-（c）p（X， Y）=0， m=n=0

1nminπ∈Πn∑mi=1d（c）（xi， yπ（i））p+cp（n－m）1/p， m≤n

d-（c）p（Y， X）， m>n（34）

式中： 1<p<∞為距離階次； c>0為截斷系數； d（c）（x， y）=min（c， d（x， y））， d（x， y）為歐氏距離； Πk表示{1， 2， …， k}的全排列； π（i）為第i種排列。 當m>n時， d-（c）p（X， Y）=d-（c）p（Y， X）。 某一時刻的勢估計等于算法估計的航跡數量。 關聯正確率、 錯誤率分別定義為跟蹤過程中正確、 錯誤關聯的量測數量與所有量測數量的比值。 航跡零碎度定義為跟蹤過程中算法估計的全部航跡數量與真實航跡數量的比值。

假設目標在三維空間中運動， 狀態向量為x=［x， x·， x¨， y， y·， y¨， z， z·， z¨］T， 目標運動模型表示為

x（k）=Fx（k－1）+w（k－1）（35）

式中： F為狀態轉移矩陣； w～N（0， Q）為零均值高斯過程噪聲。 令采樣周期為T， σ2Q為過程噪聲的功率譜密度， 則有

F=F000

0F00

00F0（36）

Q=Q0000Q0000Q0（37）

F0=1TT2/2

01T

001（38）

Q0=σ2QT5/20T4/8T3/6

T4/8T3/3T2/2T3/6T2/2T（39）

目標量測向量為z=［zTp， q， μ］T=［r， θ， φ， q， μ］T， 其中包含位置量測zp、 幅度量測q和干擾誤差角μ； 設定雷達位于坐標原點， 則位置量測模型表示為

zp（k）=h［x（k）］+vk（40）

h（x）=r～θ～φ～=x2+y2+z2arctan（y/x）

arctan（z/x2+y2）（41）

式中： v～N（0， R）為零均值高斯白噪聲， 協方差矩陣R=diag（［σ2r， σ2θ， σ2φ］）。 幅度量測使用瑞利分布模型生成， 干擾誤差角使用文獻［17］中的信號模型生成。

在跟蹤場景中設置兩個交叉運動的目標， 目標初始狀態和存活時間如表2所示， 目標1在運動過程中的加速度變化如表3所示。

目標1在第20 s釋放持續10 s的RGPO干擾， 產生4個虛假目標。 在整個干擾過程中， 虛假目標的拖引距離Rrj（t）可以表示為

Rrj（t）=0， 0≤t<t1

v（t－t1）+0.5a（t－t1）2， t1≤t<t2

關閉干擾， t2≤t<t3 （42）

式中： v表示虛假目標拖引速度； a表示拖引加速度。 干擾機在0≤t<t1處于停拖期， 在t1≤t<t2處于拖引期， t2≤t<t3處于關閉期。 在仿真中設定t1=20 s， t2=30 s， t3=50 s； 虛假目標拖引速度、 加速度如表4所示。 生成仿真量測數據所需的其他參數如表5所示。

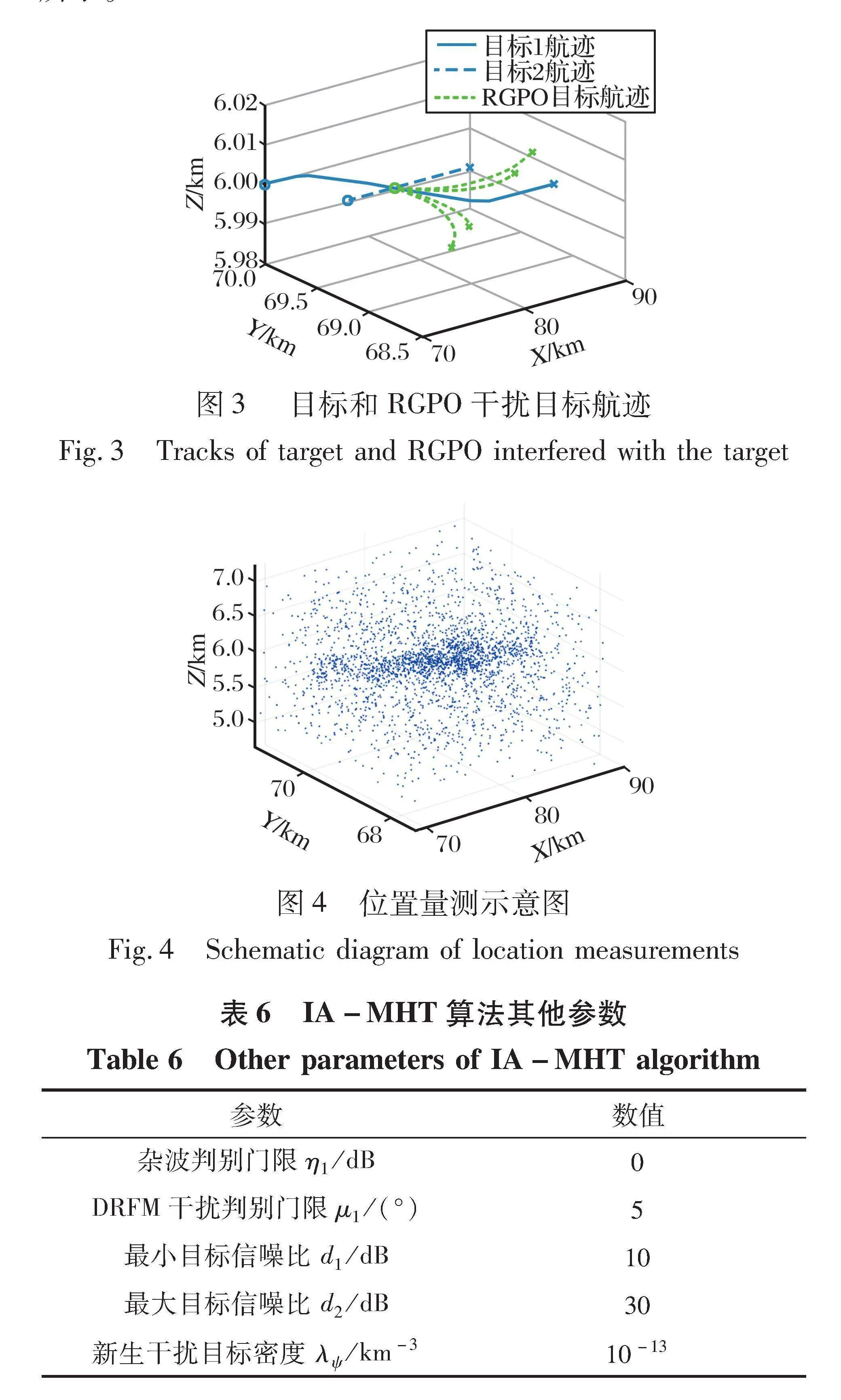
設定仿真總時長為50 s， 采樣周期T=0.1 s， 根據上述仿真參數生成的真實目標和虛假目標軌跡如圖3所示， 位置量測如圖4所示。

使用仿真數據評估傳統TOMHT算法和IA-MHT算法的性能表現。 兩種算法統一使用容積卡爾曼濾波和當前統計（Current Statistic， CS）模型進行目標狀態估計［22-23］。 設置新生目標空間密度為λν=10－13 km－3； SPRT航跡錯誤確認概率為pa=1×10－7， 航跡錯誤刪除概率為pb=1×10－5。 IA-MHT算法的其他參數如表6所示。

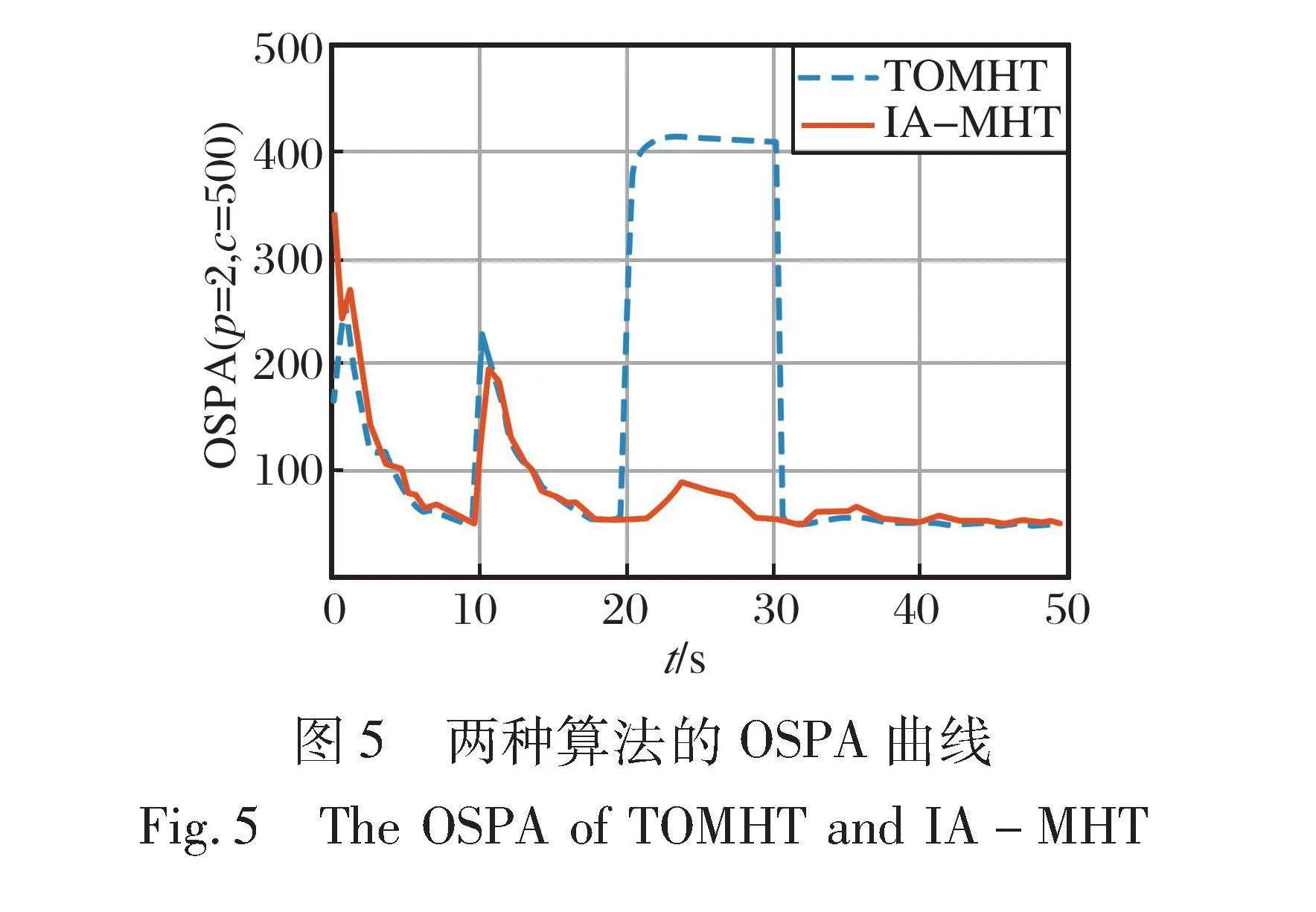
進行200次蒙特卡洛仿真， 對比TOMHT和IA-MHT算法的性能指標。 兩種算法的OSPA曲線如圖5所示， 勢估計曲線如圖6～7所示， 其他性能指標如表7所示。

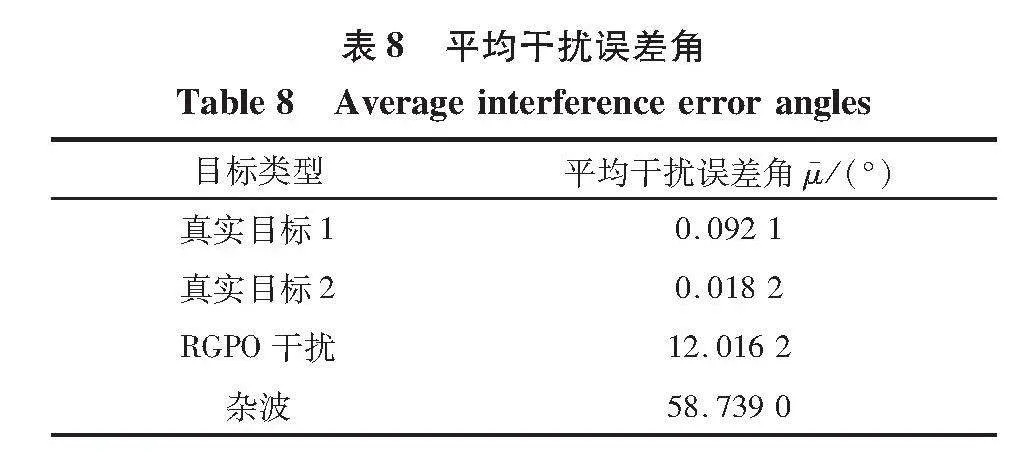
在某次仿真中， TOMHT跟蹤所得航跡如圖8所示， IA-MHT跟蹤所得航跡如圖9所示。 不同目標在跟蹤過程中的平均干擾誤差角如表8所示。

上述仿真結果表明， 利用干擾誤差角能夠有效對RGPO干擾、 雜波和真實目標進行區分。 與傳統TOMHT

算法相比， IA-MHT算法能夠有效利用雷達量測的幅度和相位信息辨別RGPO干擾量測， 從而使跟蹤結果中錯誤起始航跡數量明顯減少、 勢估計準確度有效提高； 此外， IA-MHT算法分離了干擾和目標量測的數據關聯假設生成過程， 進一步降低了關聯錯誤率和航跡零碎度； 最后， IA-MHT算法的平均運行時間僅略高于TOMHT， 兩種算法計算復雜度在同一量級， 有利于IA-MHT算法在計算資源有限的場景中得到應用。

4 結 論

本文提出了一種基于幅度和相位信息輔助的多假設跟蹤（IA-MHT）算法。 該算法利用雷達信號的幅度和相位信息實現目標真實量測和干擾量測的區分， 并改進了傳統TOMHT算法的數據關聯和航跡得分計算步驟， 從而提高算法的抗雜波、 抗干擾能力， 使雷達目標跟蹤系統在RGPO干擾環境下獲得更高的跟蹤精度和穩定性。 仿真實驗結果表明， IA-MHT算法能夠有效區分干擾量測， 降低RGPO干擾對跟蹤性能造成的不利影響； 其數據關聯準確度、 目標數量估計準確度、 航跡連續性等性能指標均優于傳統TOMHT算法。

參考文獻：

［1］ 貴彥喬， 吳彥鴻， 俞道濱. 跟蹤雷達干擾技術綜述［J］. 兵器裝備工程學報， 2017， 38（4）： 141-147.

Gui Yanqiao， Wu Yanhong， Yu Daobin. Review of Jamming Techniques to Tracker Radar［J］. Journal of Ordnance Equipment Engineering， 2017， 38（4）： 141-147.（in Chinese）

［2］ Berger S D. Digital Radio Frequency Memory Linear Range Gate Stealer Spectrum［J］. IEEE Transactions on Aerospace Electronic Systems， 2003， 39（2）： 725-735.

［3］ Wang Y H， Zhang T X， Kong L J， et al. A Stochastic Simulation Optimization-Based Range Gate Pull-off Jamming Method［J］. IEEE Transactions on Evolutionary Computation， 2023， 27（3）： 580-594.

［4］ Cheng T， He Z S， Li Y X. An Effective Target Tracking Algorithm with Anti-RGPO Ability［C］∥10th IEEE International NEWCAS Conference， 2012： 117-120.

［5］ Hou J， Yang Y， Chen Y， et al. Multiple Hypothesis Tracker in the Presence of RGPO/RGPI Using Amplitude Information［C］∥19th International Conference on Information Fusion， 2016： 703-710.

［6］ Blackman S S， Dempster R J， Busch M T， et al. IMM/MHT Solution to Radar Benchmark Tracking Problem［J］. IEEE Transactions on Aerospace and Electronic Systems， 1999， 35（2）： 730-738.

［7］ Clark D， Ristic B， Vo B N， et al. Bayesian Multi-Object Filtering with Amplitude Feature Likelihood for Unknown Object SNR［J］. IEEE Transactions on Signal Processing， 2010， 58（1）： 26-37.

［8］ Hou J， Yang Y， Wang Z W， et al. Multiple Hypothesis Tracking in the Presence of Deception Jamming Based on Multi-Feature Fusion［C］∥20th International Conference on Information Fusion， 2017： 1-8.

［9］ Reid D. An Algorithm for Tracking Multiple Targets［J］. IEEE Transactions on Automatic Control， 1979， 24（6）： 843-854.

［10］ Cox I J， Hingorani S L. An Efficient Implementation of Reid’s Multiple Hypothesis Tracking Algorithm and Its Evaluation for the Purpose of Visual Tracking［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 1996， 18（2）： 138-150.

［11］ Kuiren T. Issues in the Design of Practical Multitarget Tracking Algorithms ［M］∥Bar-Shalom Y. Multitarget-Multisensor Tracking： Advanced Applications， Norwood： Artech House， 1990： 43-87.

［12］ 王子微， 孫進平， 趙楚楚. 基于核密度雜波估計的改進MHT算法［J］. 信號處理， 2021， 37（6）： 991-999.

Wang Ziwei， Sun Jinping， Zhao Chuchu. An Improved MHT Method Based on Kernel Density Clutter Estimation［J］. Journal of Signal Processing， 2021， 37（6）： 991-999.（in Chinese）

［13］ Lerro D， Bar-Shalom Y. Automated Tracking with Target Amplitude Information［C］∥American Control Conference， 1990： 2875-2880.

［14］ Chen T， Yang P， Peng H， et al. Multi-Target Tracking Algorithm Based on PHD Filter Against Multi-Range-False-Target Jamming［J］. Journal of Systems Engineering and Electronics， 2020， 31（5）： 859-870.

［15］ Zhou C， Liu Q H， Chen X L. Parameter Estimation and Suppression for DRFM-Based Interrupted Sampling Repeater Jammer［J］. IET Radar， Sonar & Navigation， 2018， 12（1）： 56-63.

［16］ 樊會濤， 張蓬蓬. 空空導彈面臨的挑戰［J］. 航空兵器， 2017（2）： 3-7.

Fan Huitao， Zhang Pengpeng. The Challenges for Air-to-Air Missile［J］. Aero Weaponry， 2017（2）： 3-7.（in Chinese）

［17］ Greco M， Gini F， Farina A. Radar Detection and Classification of Jamming Signals Belonging to a Cone Class［J］. IEEE Transactions on Signal Processing， 2008， 56（5）： 1984-1993.

［18］ Kraut S， Scharf L L， Butler R W. The Adaptive Coherence Estimator： A Uniformly Most-Powerful-Invariant Adaptive Detection Statistic［J］. IEEE Transactions on Signal Processing， 2005， 53（2）： 427-438.

［19］ Bar-Shalom Y， Blackman S S， Fitzgerald R J. Dimensionless Score Function for Multiple Hypothesis Tracking［J］. IEEE Transactions on Aerospace and Electronic Systems， 2007， 43（1）： 392-400.

［20］ Blackman S S. Multiple Hypothesis Tracking for Multiple Target Tracking［J］. IEEE Aerospace and Electronic Systems Magazine， 2004， 19（1）： 5-18.

［21］ Li Q， Sun J P， Sun W. An Efficient Multiple Hypothesis Tracker Using Max Product Belief Propagation［C］∥20th International Conference on Information Fusion， 2017： 1-6.

［22］ Arasaratnam I， Haykin S. Cubature Kalman Filters［J］. IEEE Transactions on Automatic Control， 2009， 54（6）： 1254-1269.

［23］ Zhou H R， Kumar K S P. A "Current" Statistical Model and Adaptive Algorithm for Estimating Maneuvering Targets［J］. Journal of Guidance， Control， and Dynamics， 1984， 7（5）： 596-602.

Multiple Hypothesis Tracking Algorithm Based on Amplitude-Phase

Measurement Information Assistance

Guo Yuxia1， 2， 3*， Meng Zhongjie2 ， Liu Qi4， Fu Jiazheng1， 3

（1. China Airborne Missile Academy， Luoyang 471009， China;

2. School of Astronautics， Northwestern Polytechnical University， Xi’an 710072， China;

3. National Key Laboratory of Air-based Information Perception and Fusion， Luoyang 471009， China;

4. Project Center of Air Force Equipment Department， Beijing 100843， China）

Abstract： In range gate pull off （RGPO） jamming scenarios， conventional multiple target tracking algorithm can not effectively distinguish the RGPO deception from real target measurements， resulting in track mis-initialization， increased tracking error， and tracking discontinuity. This paper proposes an information-assisted multiple hypothesis tracking （IA-MHT） algorithm to solve the above problems. The IA-MHT algorithm utilizes amplitude and phase information of radar measurements to distinguish between true and false measurements of targets. Furthermore， the algorithm adjusts the calculation method of global association hypothesis probabilities and track scores， which improves the tracking performance under clutter and RGPO interferences. Simulation results show that the IA-MHT algorithm can effectively distinguish the RGPO deception measurements and obtain superior data association performance compared to the conventional MHT algorithm.

Key words： multiple hypothesis tracking; range gate pull off jamming; information assistance; track score