統(tǒng)領(lǐng)全章 突破難點

我們在小學(xué)階段已經(jīng)初步接觸到與概率有關(guān)的知識，感受到隨機現(xiàn)象發(fā)生的可能性是有大小的。進入初中階段，我們在八（下）第8章學(xué)習了“認識概率”，通過進一步抽象化、數(shù)學(xué)化地研究，了解到概率是對隨機現(xiàn)象的一種數(shù)學(xué)描述，刻畫隨機事件發(fā)生的可能性的大小。對于九（上）“等可能條件下的概率”，我們主要研究如何在等可能條件下計算簡單隨機事件的概率。學(xué)習本章知識的關(guān)鍵點在于統(tǒng)領(lǐng)全章、突破難點，以此掌握求解概率的方式方法。

統(tǒng)籌并進，涵蓋全章

“等可能條件下的概率”這一章所涵蓋的內(nèi)容及知識點眾多。為了提高學(xué)習效果，我們需要有全局思維，能夠系統(tǒng)梳理本章知識要點，熟練掌握知識之間的相互關(guān)聯(lián)，構(gòu)建完整的知識結(jié)構(gòu)，通過知識的橫向連接促進能力素養(yǎng)的縱向發(fā)展。具體而言，以“概率定義→等可能條件下的概率的基本特征→等可能條件下的概率的計算→概率的應(yīng)用”為主線，可以幫助我們更好地理解內(nèi)容和應(yīng)用知識。在本章的學(xué)習過程中，我們首先要理解相關(guān)概念，如概率定義、兩大基本特征（等可能性和有限性）、計算公式等。其次，我們要掌握求解概率的方式方法，如列表法、畫樹狀圖法、轉(zhuǎn)化法等，并從中體會概率的模型思想。

突破難點，求解概率

本章知識難點主要有兩個：一是判斷隨機試驗結(jié)果是否具有等可能性；二是求解一些隨機事件發(fā)生的概率。在判斷過程中，我們需要不重復(fù)、不遺漏地列出所有等可能出現(xiàn)的結(jié)果。教材中介紹了兩種列舉方法：列表法和畫樹狀圖法，這兩種方法各有優(yōu)勢和特點。當試驗結(jié)果分為兩步，并且所有等可能出現(xiàn)的結(jié)果數(shù)較少時，運用這兩種方法都比較快速有效；當試驗結(jié)果分為兩步，但所有等可能出現(xiàn)的結(jié)果數(shù)較多時，運用列表法更為簡捷合適；當試驗結(jié)果分為三步或更多時，運用樹狀圖更加簡便合適。

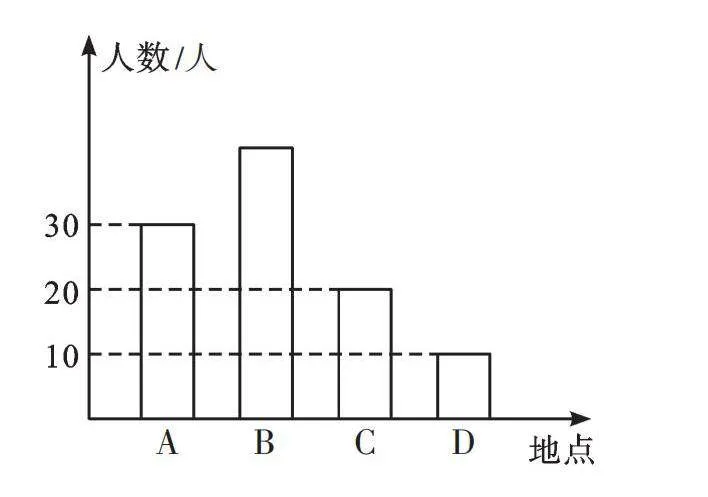
例題 國慶節(jié)快到了，北京某初中學(xué)校準備組織部分學(xué)生分別到頤和園（A）、故宮（B）、人民大會堂（C）、水立方（D）四個地方參加慶祝活動。請根據(jù)所繪制的條形統(tǒng)計圖回答問題：

（1）若到故宮（B）參加慶祝活動的人數(shù)為總?cè)藬?shù)的40%，則到故宮（B）的人數(shù)是多少？

（2）現(xiàn)有4張相同的小紙條，上面分別標記整數(shù)1、2、3、4，放在一個盒子中攪勻，先由妹妹從中任意摸出一張紙條，摸完后放回、攪勻，再由哥哥從中任意摸出一張紙條。若摸出的兩張紙條上的數(shù)字之和為3的倍數(shù)，則妹妹獲勝；若為5的倍數(shù)，則哥哥獲勝。請問這種方法公平嗎？

【解析】（1）設(shè)到故宮的人數(shù)是x。由圖可得[x30+x+20+10]=40%，解得x=40（人）。

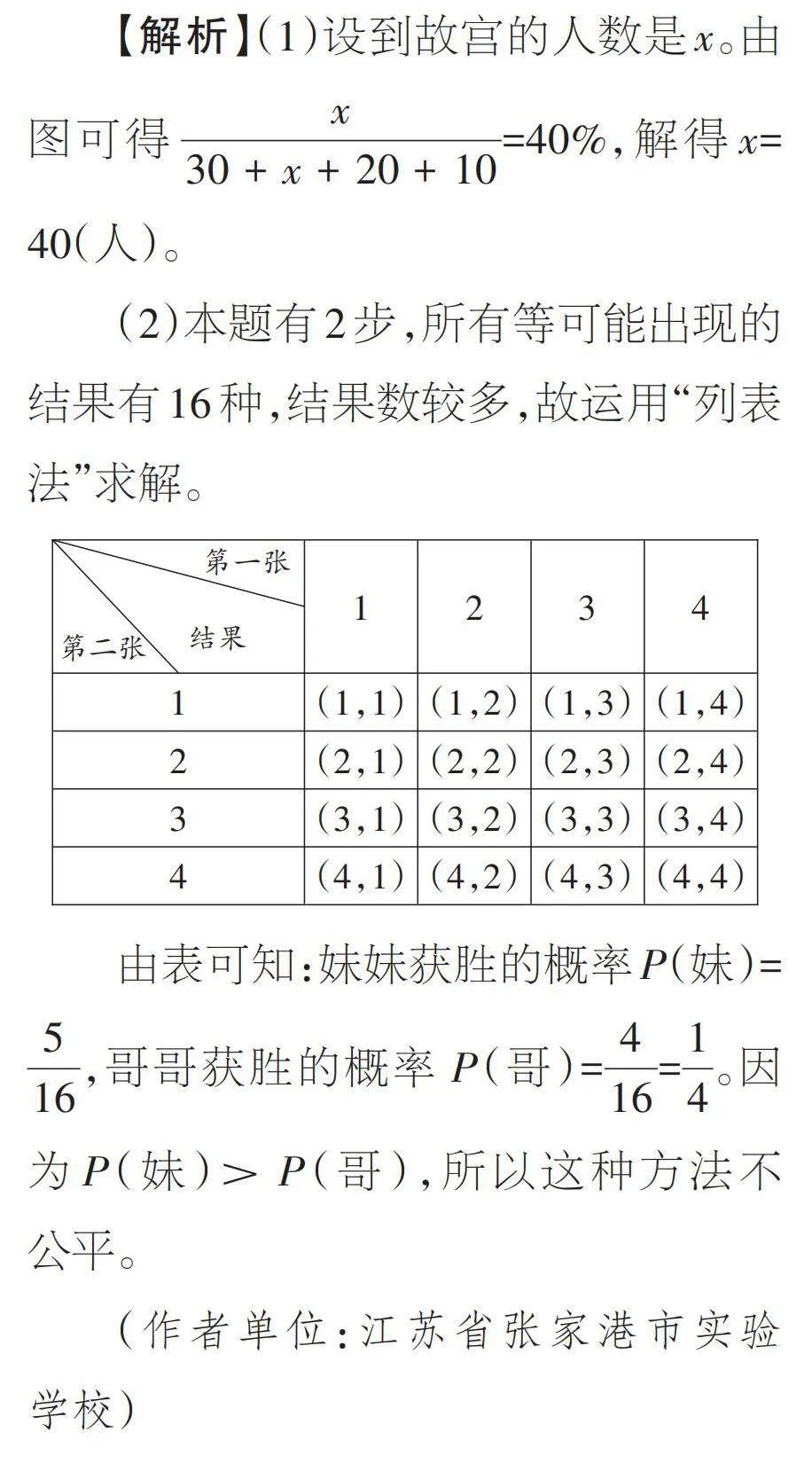
（2）本題有2步，所有等可能出現(xiàn)的結(jié)果有16種，結(jié)果數(shù)較多，故運用“列表法”求解。

由表可知：妹妹獲勝的概率P（妹）=[516]，哥哥獲勝的概率 P（哥）=[416]=[14]。因為P（妹）＞ P（哥），所以這種方法不公平。

（作者單位：江蘇省張家港市實驗學(xué)校）