數據背后的秘密

數據分析被廣泛應用于科技、農業等領域，讓我們的決策更加科學化、個性化。下面，我們以2024年安徽的中考題為例，一起探究數據背后的秘密。

例題 （2024·安徽）綜合與實踐

【項目背景】無核柑橘是我省西南山區特產，該地區某村有甲、乙兩塊成齡無核柑橘園。在柑橘收獲季節，班級同學前往該村開展綜合實踐活動，其中一個項目是：在日照、土質、空氣濕度等外部環境基本一致的條件下，對兩塊柑橘園的優質柑橘情況進行調查統計，為柑橘園的發展規劃提供一些參考。

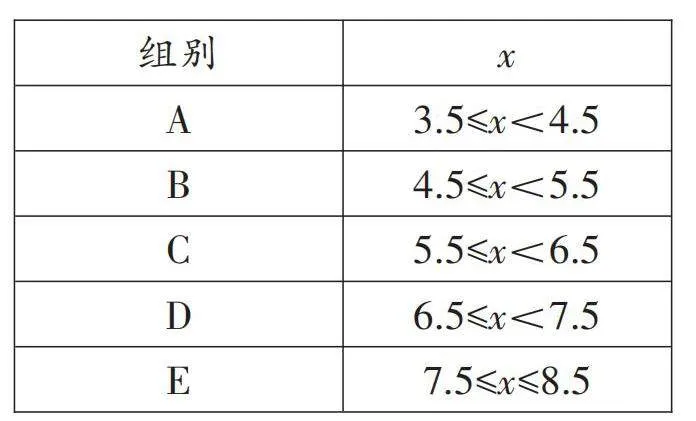
【數據收集與整理】從兩塊柑橘園采摘的柑橘中各隨機選取200個。在技術人員指導下，測量每個柑橘的直徑，作為樣本數據。柑橘直徑用x（單位：cm）表示。將所收集的樣本數據進行分組：

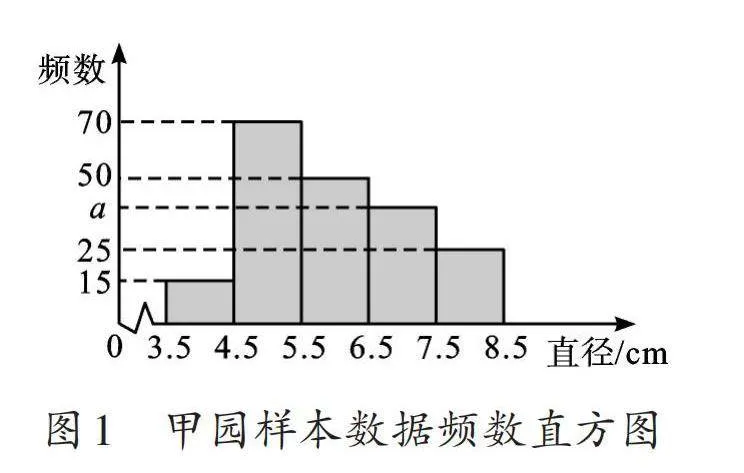
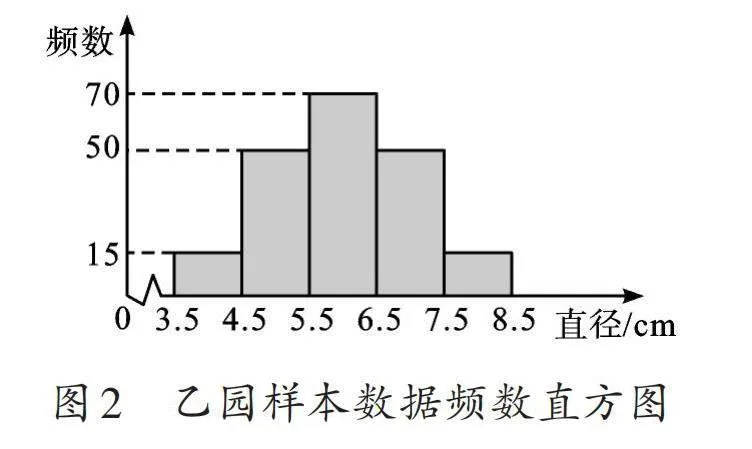
整理樣本數據，并繪制甲、乙兩園樣本數據的頻數直方圖，部分信息如下：

任務1 求圖1中a的值。

【數據分析與運用】任務2 A，B，C，D，E五組數據的平均數分別取為4，5，6，7，8，計算乙園樣本數據的平均數。

任務3 下列結論正確的是_______。①兩園樣本數據的中位數均在C組；②兩園樣本數據的眾數均在C組；③兩園樣本數據的最大數與最小數的差相等。

任務4" 結合市場情況，將C、D兩組的柑橘認定為一級，B組的柑橘認定為二級，其他組的柑橘認定為三級，其中一級柑橘的品質最優，二級次之，三級最次。試估計哪個園的柑橘品質更優。

【解析】（1）用200減去其他各組的頻數可得a=200-（15+70+50+25）=40。（2）根據加權平均數的計算公式可得[1/200]×（15×4+50×5+70×6+50×7+15×8）=6，所以乙園樣本數據的平均數為6。（3）由統計圖可知，兩園樣本數據的中位數均在C組，①正確；甲園的眾數在B組，乙園的眾數在C組，②錯誤；兩園樣本數據的最大值與最小值的差不一定相等，③錯誤。（4）乙園的柑橘品質更優，因為從樣本數據頻數分布直方圖可知，乙園一級柑橘占比大于甲園。

【點評】本題綜合考查了頻數分布直方圖、樣本估計總體、頻數分布表、加權平均數、中位數、眾數和極差，讀懂圖象信息是解題的關鍵。

（作者單位：江蘇省興化市昭陽湖初級中學）