一種非平滑相干干擾魯棒的自適應波束形成器

摘 要：

針對文獻報道的魯棒自適應波束形成（robust adaptive beamforming， RAB）算法，分析了在存在相干干擾時其性能嚴重下降甚至失效的原因：通過將接收信號協方差矩陣分解為陣列流形矩陣左和共軛右乘一個矩陣P的描述形式，在存在相干干擾時，P為非對角陣，其非對角元素表征了信號與干擾間的互相關，該成分造成了RAB算法的失效;另表明：快拍數有限可視為特殊的相干干擾情況。為此，提出了一種構建P為對角陣的協方差矩陣擬合方法;并據擬合的協方差矩陣，給出了對非平滑相干干擾RAB方法。仿真驗證了分析的有效性，所提方法在相干干擾時仍能實現非相干干擾時的性能，且收斂速度優于報道方法。

關鍵詞：

魯棒自適應; 波束形成; Capon譜; 相干干擾; 協方差矩陣擬合

中圖分類號：

V 243.2

文獻標志碼： A""" DOI：10.12305/j.issn.1001-506X.2024.05.01

A robust adaptive beamformer with non-smoothing coherent interference

LU Wenlong， LI Dan*， BI Quanyang， ZHANG Jianqiu

（School of Information Science and Engineering， Fudan University， Shanghai 200433， China）

Abstract：

The robust adaptive beamforming （RAB） algorithms reported in the literature are analyzed， to explain the serious performance degradation or even completely invalid in the presence of coherent interference. When the covariance matrix of the received data is decomposed into the description form of the array manifold matrix left and conjugate right multiplied by a matrix P. P is a non-diagonal matrix when the received data are interfered by the coherent signal sources， and the off-diagonal elements in the matrix P represent the coherences between the signal and interference sources as well as among interference ones， which are the main reasons for the failure of RAB algorithm reported in the literature. It is shown further that the insufficient number of snapshots can be regarded as a special case of coherent interference. In order to deal with these situations， a covariance matrix fitting method is proposed by constructing P as a diagonal matrix. Based on the fitted covariance matrix， an RAB method for non-smooth coherent interference is presented. The simulation results verify the effectiveness of the analytical ones. Meanwhile， they also show that the proposed method can still achieve the performances of the non-coherent interference RAB algorithms in the case of coherent interference， and has a faster convergence rate than the methods reported in the literature.

Keywords：

robust adaptive; beamforming; Capon spectrum; coherent interference; covariance matrix fitting

0 引 言

自適應波束形成是陣列信號處理的基礎技術，它已經廣泛應用于雷達、聲納、通信、醫療成像以及其他領域［1-5］。在各種波束形成器中，Capon自適應波束形成器是可能最大化輸出信干噪比（signal-to-interference-plus-noise-ratio， SINR）的最優空域波束形成器［6］。在過去數十年的研究中，文獻報道了大量基于非相干假設的魯棒自適應波束形成（robust adaptive beamforming， RAB）技術，然而當感興趣信號（signal of interest， SOI）和/或干擾之間相干時，RAB算法將會由于信號和/或各干擾之間的相干，而產生嚴重的性能損失。

為應對相干干擾的問題，文獻也報道了一系列利用空間平滑技術的魯棒波束形成器。例如，文獻［7］提出的托普利茲矩陣重構算法，即試圖通過采樣協方差矩陣（sampling covariance matrix， SCM）沿著對角線進行平均，以保留采樣協方差矩陣的托普利茲特性。文獻［8］則將整個陣列拆分成數個子陣列，以各個子陣列的協方差矩陣的均值，作為設計波束形成矢量的采樣協方差矩陣，并以此對相干信號進行解耦。文獻［9］將前后向子陣列輸出的自相關矩陣，進行互相關后矩陣的平均，視為糾正的空間平滑矩陣，提升了空間平滑魯棒波束形成器的性能。近年來，文獻［10-12］則進一步研究了基于空間平滑的相干魯棒波束形成算法，這些方法能對相干信號進行有效的解耦，然而，它們無法克服空間平滑算法的固有缺點：即以犧牲陣列的有效孔徑為代價，來換取對相干干擾的魯棒性［12］。

近年來，在不存在相干干擾的前提下，文獻報道了一系列的RAB方法，在總體上可將可它們分為：對角加載［13-14］、特征空間投影［15-16］、不確定集約束［17-20］和噪聲干擾協方差矩陣（interference-plus-noise covariance matrix， INCM）重構4類。而基于INCM重構方法所表現出來的優越性能，就成為最近來魯棒波束成形器的研究熱點，這些方法可分為3種。第1種方法從SCM或者改善SCM中移除SOI［21-22］;第2種方法通過在干擾存在的角域對Capon譜進行積分，而重構INCM［23-24］;第3種則是：首先估計出所有信號和干擾的導向矢量及功率，以及噪聲的功率而對INCM進行重構［25-29］。與前兩種方法相比，第3種方法完全移除了SOI成分，因此就能夠獲得更準確的INCM［29］。例如，文獻［25］在信號和干擾源稀疏分布的基礎上，通過求解壓縮感知問題而重構INCM，這種稀疏重構的方法，在較大的信噪比（signal to noise ratio， SNR）范圍內，都有著近乎最優的性能。文獻［29］分析了干擾功率估計對于RAB的影響，進而提出了一種通過簡單干擾功率估計，而可對INCM進行重構的方法，該方法在達到與［25］相同性能的同時，簡化了計算過程。然而這些方法，在沒有其他先驗知識的情況下，不得不利用采樣協方差來對陣列接收快拍進行Capon譜搜索［25，29］，以獲得信號和干擾的譜，以獲取對SOI和干擾的功率，以及它們導向矢量的估計，而重構INCM。可是，相干干擾引起采樣協方差估計的虧秩和誤差，就必將影響Capon譜的搜索結果，進而影響重構的INCM，以致最終就會影響據其而設計波束成形器的性能。

在不犧牲陣列天線有效孔徑的前提下，本文擬研究對相干干擾魯棒的波束形成方法，并期待其能達到非相干魯棒波束形成其的性能。為此，本文首先對陣列接收信號的協方差矩陣進行了分析。分析表明：當SOI和/或各干擾間相干時，陣列接收信號的互協方差矩陣，將不可避免地包含SOI成分，這就會導致基于采樣協方差構建的INCM與理想INCM存在較大不同，并將導致Capon類的波束形成器性能下降，甚至完全失效。而進一步的分析則表明：將協方差矩陣R分解為導向矢量矩陣A左乘一個矩陣P，再右乘A的共軛轉置形式，即

R=APAH

式中：（·）H表示共軛轉置，那么P矩陣的對角線元素，將對應著SOI與干擾的功率，而其非對角線元素，則將對應于SOI與干擾的互相關成分。如果能消除協方差矩陣R中的互相關成分，即消除P矩陣的非對角元素，那么在不采用空間平滑技術的條件下，也可使RAB算法在相干干擾時保持與非相干干擾時同樣的性能。分析也表明：當對采樣協方差矩陣進行分解時，即使是陣列接收數據未受到相干的干擾，但由于快拍數的不足或有限，SOI、干擾和噪聲之間，依然會存在著互相關成分，換言之，分解后的P矩陣，同樣存在著影響波束形成器性能的非對角元素。以這一觀點出發，就發現了文獻［21］報道的RAB算法，即使沒有相干干擾而快拍數不足或有限時，P矩陣存在著非對角元素，這一點就與相干干擾時面對的問題相同，也就是說，快拍數不足或有限可視作一種特殊的相干干擾。

為了應對這些情況，本文進而提出了一種通過構建P為對角陣，以加權最小二乘準則獲得不含信號與干擾，以及干擾與干擾互相關成分的協方差矩陣擬合方法，據擬合的協方差矩陣，進而給出了對非平滑相干干擾魯棒的RAB方法。仿真驗證了分析結果的有效性，同時它們也表明：提出的方法，在相干干擾時仍能實現非相干干擾RAB算法的性能，以及具有更快的收斂速度，且其性能優于文獻報道的方法。

本文其他內容安排如下：第1節包括問題模型與相干干擾的分析;第2節在第1節分析的基礎上提出本文的RAB算法;第3節為仿真部分;第4節對全文進行總結。

1 信號模型與問題背景

1.1 Capon波束形成器

考慮一個由M個全向陣元組成的均勻線陣（uniform linear array， ULA），有N個窄帶信號（一個SOI與N－1個干擾）從θ1，θ2，…，θN方向入射到陣列，那么在k時刻陣列的觀測［1］可以建模為

2.4 復雜度分析

在本節將分析本文方法的計算復雜度，并將與文獻［23，29］報道的兩種基于INCM重構方法的計算復雜度進行比較。本文方法的計算代價，主要是協方差矩陣的重構及其求逆，以及譜峰搜索過程。重構協方差矩陣過程復雜度為O（M2L），協方差矩陣求逆過程復雜度為O（M3），由于最多可分辨M個信號，譜峰搜索過程為O（M2L）。文獻［23］方法的計算復雜度，主要由INCM的重構與SOCP問題求解組成，計算復雜度為O（M2S）+O（M3.5），其中S表示干擾可能存在區域內的采樣格點數。文獻［29］方法的計算，主要包括譜峰搜索與特征值分解，計算復雜度為O（M2L）+O（M3）。考慮到本文的迭代過程，以及在后續數值仿真中經驗，本文方法計算量高于文獻［29］的方法，比文獻［23］的方法效率更高。

3 數值仿真實驗

在仿真實驗中，選擇全向陣元間距為半波長，且M=10的均勻線陣，加性噪聲為復高斯零均值的空時白噪聲過程，并且每個陣元噪聲方差相同。假設SOI從方向θ1=5°入射到陣列，3個干擾分別來自方向θ2=－50°、θ2=－20°和θ3=30°，除第3.1.2節的仿真實驗外，假設干擾和SOI間不相干。每個陣元干噪比（interference to noise ratio， INR）為30 dB，且噪聲方差設定為σ2n=1 W，干擾功率為30 dBW。除SNR變化的實驗外，輸出SNR固定為20 dB，除快拍數變化的仿真實驗外，快拍數固定為K=30。對基于重構的波束形成器，假設SOI可能的角域為Θ=［θ1－5°，θ1+5°］，干擾或散射徑的角域為Θi=［θi－5°，θi+5°］（i=2，3，4），每個仿真均進行500次蒙特卡羅實驗。采樣格點間隔為0.1°。性能評價指標為據式（6）計算的SINR，在部分圖中使用了最優SINR的偏差。由下式計算無SOI的INCM為

R^i+n=∑Ni=2∑Kk=1xi（k）xHi（k）K+∑Kk=1n（k）nH（k）K（35）

式（35）獲得的理想結果，是無法通過陣列接收數據恢復的，它將在本節中作為輸出SINR最優的波束形成器，而視為對比對象，在后面將以SOI-free表示。

3.1 INCM重構方法比較

本節將通過數值仿真比較不同INCM重構方法的有效性。假設SOI準確且已知。其他比較的波束成形器為：SMI-SOI表示在SCM中減去SOI成分而設計的波束形成器、基于重構估計（reconstruction estimation based， REB）的波束形成器［23］，以及簡化干擾功率估計的波束形成器（simplified interference power estimation， SIPE）［29］。在本節的兩個仿真實驗中，所有方法的SOI導向矢量均采用假定SOI導向矢量即a（5°）。

3.1.1 干擾不相干

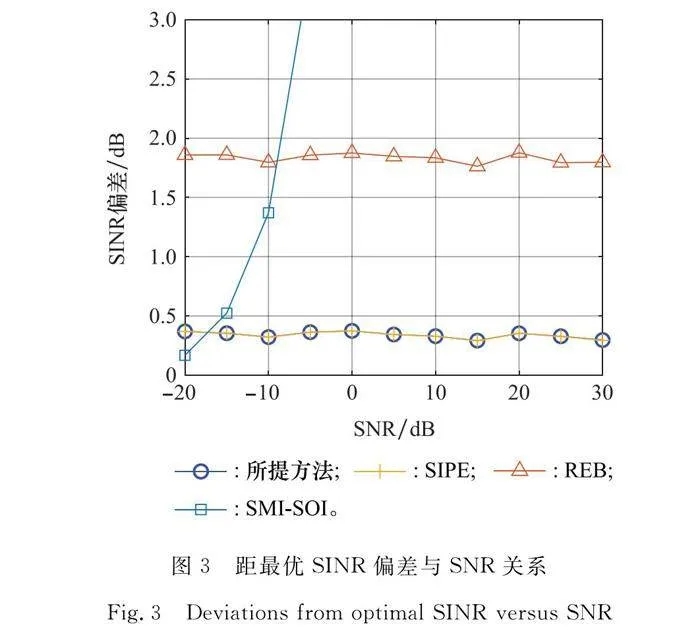
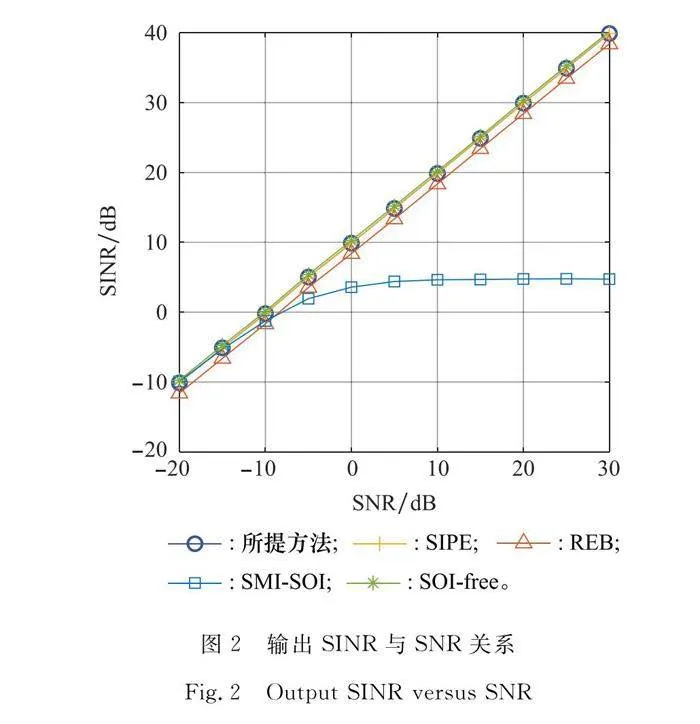
圖2給出了在信源間都互不相關情況下，各波束形成器輸出SINR隨SNR變化情況，為清晰顯示各方法間的差距，圖3給出了不同波束形成器輸出SINR與最優SINR偏差隨SNR的變化情況。可以發現：本文提出方法與SIPE始終與最優輸出SINR重合（SOI-free），REB與最優輸出SINR具有一定的差距。隨著SNR的增加，SOI的功率將逐漸增大，以致SMI-SOI方法構造的INCM中，其R^cross成分就將逐漸增加，這就使得其與理想INCM偏差逐漸變大，而使得由其設計的波束成形器性能逐漸變差。

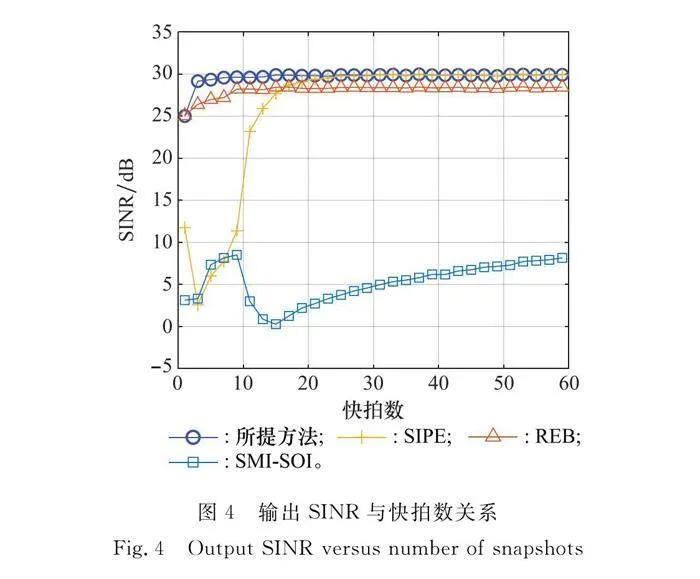
圖4顯示了不同波束形成器輸出SINR與接收信號快拍數的關系。本方法在單快拍情況下也具有25 dB的輸出SINR，并在3快拍時基本收斂。在約25快拍時，SIPE波束形成器的輸出SINR收斂，而在快拍數10以下時，有著15 dB以上的性能損失。在低快拍數的情況下，Capon譜估計的性能下降，從而影響了SIPE的干擾導向矢量估計，以致其輸出SINR與最優SINR存在較大差距。REB波束形成器在單快拍時性能損失也僅有5 dB，在快拍數為9時基本收斂，這是因為該方法在重構INCM時，僅對干擾可能存在區域內的Capon譜進行了積分，充分利用了先驗信息;然而這樣的策略，也使得即使在快拍數足夠時，也不能準確地重構INCM，因此就有著約2 dB的性能損失。在圖4中，SMI-SOI波束形成器一直未收斂，在我們仿真實驗中，該方法在250快拍時仍未收斂。

3.1.2 干擾相干

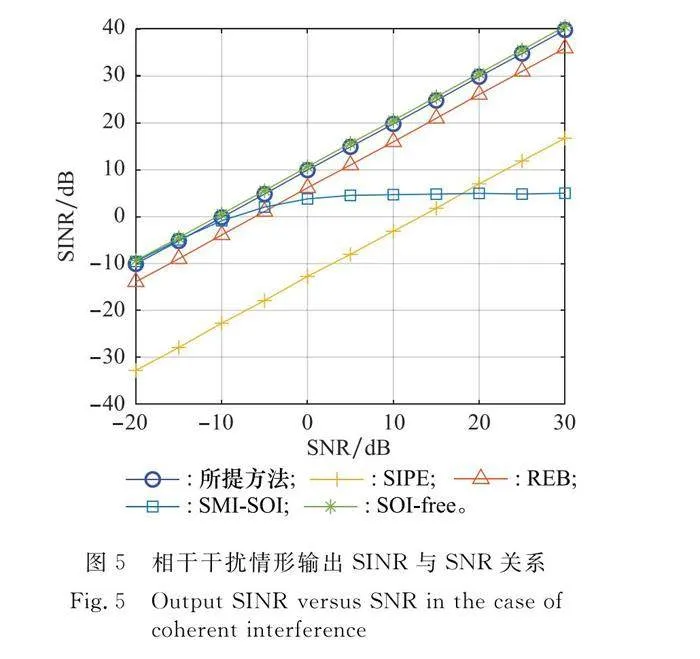
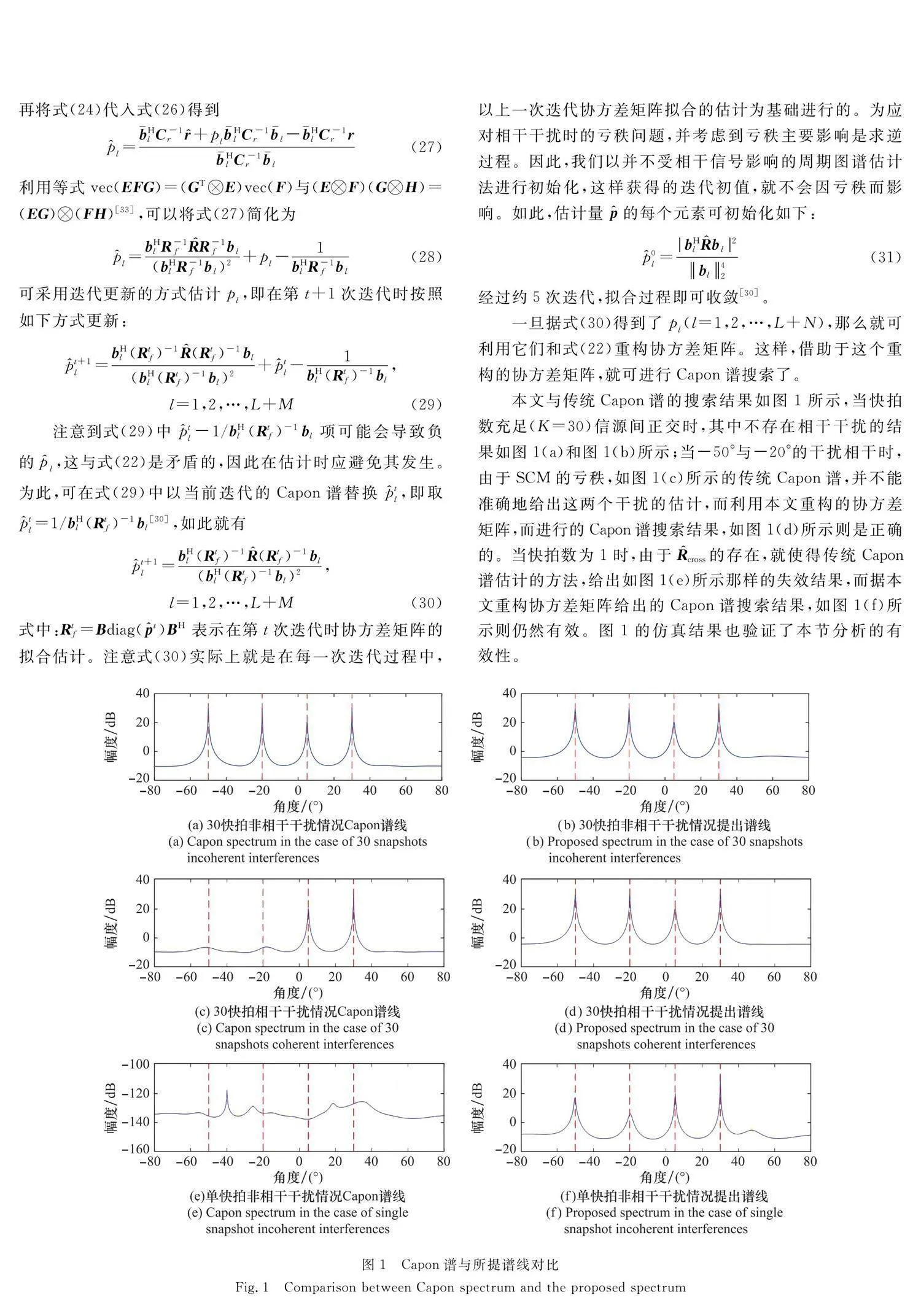
圖5給出了來自－50°與－20°的干擾相干時，不同波束形成器輸出SINR與SNR關系圖。可以看到，此時SIPE出現了嚴重的性能下降。這是因為此時如圖1（c）給出的Capon譜，不能給出來自－50°與－20°這兩個方向干擾導向矢量的估計，而SIPE在INCM重構時忽略了這兩個干擾，從而導致了波束形成器輸出與最優SINR有著約22 dB的性能差距。而本文提出方法的性能與非相干干擾情況下沒有區別，與最優輸出SINR僅有約0.3 dB的差距。REB方法由于充分利用了干擾位置的先驗信息，相比非相干干擾時性能沒有下降。SMI-SOI方法則性能與前述實驗完全一致。

圖6是相干干擾情況下，不同波束形成器輸出SINR與快拍數之間關系圖。本文提出方法保持著非相干干擾時的優秀性能，在單快拍時仍然有著約25 dB的輸出SINR，并且在有3個快拍時即收斂。SIPE依舊直至20快拍以上才收斂。在相干干擾下，REB波束形成器，在10快拍以下時的性能顯著下降，與最優SINR有著約25 dB的差距。

3.2 波束形成器輸出SINR比較

在本節中，將對兩個具有實際價值的應用場景進行仿真驗證，并將本文方法與REB波束形成器［23］、SIPE波束形成器［29］、最差性能優化（worst case performance optimization， WCPO）波束形成器［17］，以及加載SMI（loaded SMI， LSMI）［4］進行了對比。REB方法假設已知所有干擾或散射徑的角域Θi（i=2，3，4），WCPO中因子ε設置為0.3，LSMI的加載系數設置為10。

3.2.1 隨機陣列視向誤差

假設SOI與干擾都受到陣列視向誤差的影響，并產生隨機的DOA失配，失配的DOA是在［－4°，4°］內均勻分布，也就是說SOI的DOA均勻分布在［1°，9°］之間，3個干擾的DOA分別均勻分布在［－54°，－46°］、［－24°，－16°］、以及［26°，34°］間。SOI與干擾的DOA在仿真實驗之間是變化的，但在單次仿真實驗的快拍間保持不變。

圖7給出了在存在隨機視向誤差的情況下，不同方法輸出SINR與最優輸出SINR之間的偏差，以及與SNR關系圖。在SNR低于-5 dB時，由于譜峰與偽峰難以分辨，提出方法與SRC的SOI導向矢量均采用假設導向矢量即a（5°），因此相較于最優SINR有著0.8 dB左右的偏差;而在SNR高于-5 dB時，兩種方法均以SOI內的譜峰位置，作為SOI的導向矢量，此時它們與最優的SINR，僅有0.3 dB的性能偏差。REB波束形成器則與上一小節仿真驗相同，有1.8 dB的性能偏差。由于仿真情況并不總是最差性能的情形，因此，WCPO波束形成器在高SNR時，性能急劇下降。由于LSMI的最優加載因子難以確定，因此低SNR有效的加載因子，在高SNR時可能會失效。

圖8則給出了不同波束形成器收斂速度的對比，本文提出方法仍然有著最快的收斂速度與單快拍表現，兩種高性能對比方法SIPE與REB在10快拍以下性能損失嚴重。WCPO與LSMI方法在10快拍時收斂。

3.2.2 耦合多徑

假設由于散射體造成的多徑散射效應，會使得期望信號發生耦合而產生散射，為此本節仿真了存在下面1個直射徑與3個散射徑的情況：

a=a（θs）+∑3γ=1ejγa（θγ）（36）

式中：a（θγ）（γ=1，2，3，4）為耦合散射徑;在每個仿真實驗中，θγ（γ=1，2，3）分別為－50°、－20°和30°;相位γ（γ=1，2，3，4）均勻獨立地分布于［0，2π］之間。γ在不同仿真之間變化，在同一仿真的不同快拍之間保持不變。

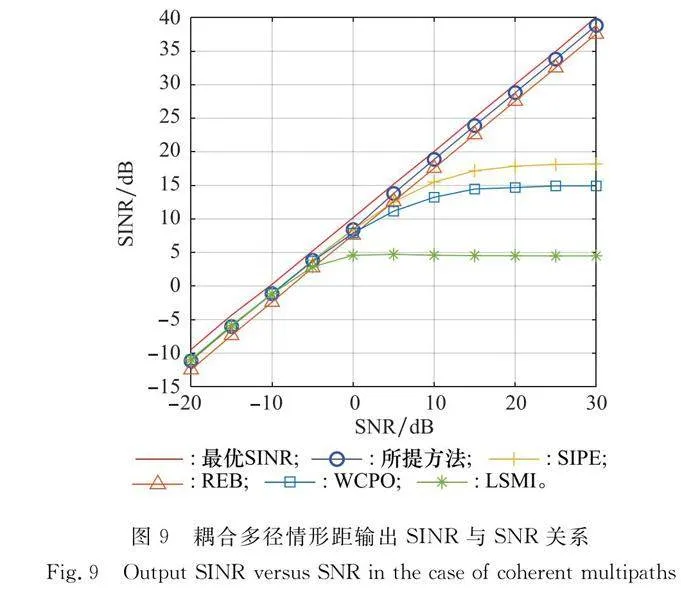
圖9給出了在耦合多徑的情況下，不同波束形成器輸出SINR隨SNR變化的關系。在SNR低于-10 dB時，各方法性能差距不大，因為此時INCM以噪聲成分為主。隨著SNR增加，本文提出方法性能始終與最優SINR差距最小。LSMI方法、WCPO方法與SIPE方法逐漸失效影響。REB方法表現出僅次于本文方法的性能，是因為該方法利用了干擾DOA角域的先驗信息，當DOA估計不可靠時，該方法將失效。因此本文提出方法在耦合多徑時具有最優性能。

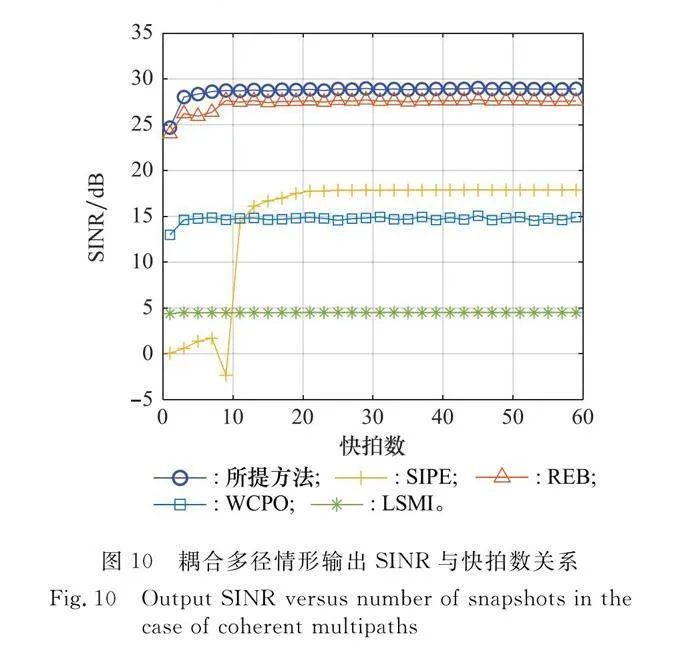
圖10比較了不同波束形成器的收斂速度，本文提出方法在少于10快拍數情況下，仍然有著接快拍數充足時的性能。僅有利用了干擾DOA先驗信息的REB方法與本文方法相近，該方法在低快拍數時，性能損失比本文方法更多。SIPE方法則表現出最慢的收斂速度，在25快拍時才收斂。因此本文提出方法在低快拍數時，例如10快拍以下，仍然具有接近最優的性能。

4 結 論

本文首先分析了在存在相干干擾情況下，魯棒波束成形算法性能會嚴重下降，甚至完全失效的原因，并提出了相應的非平滑相干干擾RAB算法，結論如下：將協方差矩陣分解為導向矢量矩陣左和其共軛右乘一個矩陣P的描述形式，矩陣P在相干干擾下為非對角陣，其非對角元素表征了信號與干擾，以及干擾與干擾的互相關，并表明這些成分是造成文獻報道RAB算法失效的主要原因。進一步的分析表明：快拍數不足或有限，可視為一種特殊的相干干擾情況。本文提出了一種通過構建矩陣P為對角陣，以獲得一個不含信號與干擾，以及干擾與干擾互相關成分的協方差矩陣擬合方法，據擬合的協方差矩陣，進而給出了一種對非平滑相干干擾魯棒的RAB方法。數值仿真驗證了分析結果的有效性，數值仿真也表明：提出的方法在相干干擾時仍能實現非相干干擾RAB算法的性能，同時提出的方法具有更快的收斂速度，且其性能優于文獻報道的方法。

參考文獻

［1］ LI J， STOICA P. Robust adaptive beamforming［M］. New York： Wiley， 2005.

［2］ 王永良， 丁前軍， 李榮鋒. 自適應陣列處理［M］. 北京： 清華大學出版社， 2009.

WANG Y L， DING Q J， LI R F. Adaptive array processing［M］. Beijing： Tsinghua University Press， 2009.

［3］ 汪晉寬， 宋聽. 魯棒自適應陣列信號處理［M］. 北京： 電子工業出版社， 2009.

WANG J K， SONG T. Robust adaptive array signal processing［M］. Beijing： Electronic Industry Press， 2009.

［4］ 袁曉壘. 魯棒自適應波束形成算法研究［D］. 成都： 電子科技大學， 2017.

YUAN X L. Research on robust adaptive beamforming algorithm［D］. Chengdu： University of Electronic Science and Technology， 2017.

［5］ 畢權楊， 李旦， 張建秋. 空時自適應處理張量波束成形器的外積合成法［J］. 航空學報， 2019， 40（10）： 158-170.

BI Q Y， LI D， ZHANG J Q. The outer product synthesis method of space-time adaptive processing tensor beamformer［J］. Journal of Aeronautics， 2019， 40（10）： 158-170.

［6］ CAPON J. High-resolution frequency-wavenumber spectrum analysis［J］. Procceedings of the IEEE， 1969， 57（8）： 1408-1418.

［7］ KUNG S， LO C， FOKA R. A Toeplitz approximation approach to coherent source direction finding［C］∥Proc.of the IEEE International Conference on Acoustics， Speech， and Signal Processing， 1986： 193-196.

［8］ MAHESWARA K， REDDY V U. Analysis of spatial smoothing with uniform circular arrays［J］. IEEE Trans.on Signal Processing， 1999， 47（6）： 1726-1730.

［9］ WU X D， MA L， LIANG Z H. Improved weighted spatial smoothing algorithm［J］. Journal of Data Acquisition and Processing， 2015， 30： 824-829.

［10］ GUO Y， ZHANG L， ZHANG J， et al. A coherent signal beamforming technique based on sub-array cross correlation［J］. Digital Signal Processing， 2022， 121： 1051-2004.

［11］ DU Y， CUI W J， MEI F T， et al. Coherent signals adaptive beamforming algorithm based on eigenvalue［C］∥Proc.of the 2nd International Conference on Electronics， Communications and Information Technology， 2021： 388-393.

［12］ ZHANG L， LIU W. Robust beamforming for coherent signals based on the spatial-smoothing technique［J］. Signal Processing， 2012， 92（11）： 2747-2758.

［13］ COX H， ZESKIND R M， OWEN M M. Robust adaptive beamforming［J］. IEEE Trans.on Acoustics， Speech， Signal Processing， 1987， 35（10）： 1365-1376.

［14］ DU L， LI J， STOICA P. Fully automatic computation of diagonal loading levels for robust adaptive beamforming［J］. IEEE Trans.on Aerospace and Electronic Systems， 2010， 46（1）： 449-458.

［15］ FELDMAN D D. An analysis of the projection method for robust adaptive beamforming［J］. IEEE Trans.on Antennas Propagation， 1996， 44（7）： 1023-1030.

［16］ JIA W M， JIN W， ZHOU S H， et al. Robust adaptive beamforming based on a new steering vector estimation algorithm［J］. Signal Processing， 2013， 93（9）： 2539-2542.

［17］ VOROBYOV S A， GERSHMAN A B， LUO Z Q. Robust adaptive beamforming using worst-case performance optimization： a solution to the signal mismatch problem［J］. IEEE Trans.on Signal Processing， 2003， 51（2）： 313-324.

［18］ LI J， STOICA P， WANG Z S. Doubly constrained robust Capon beamformer［J］. IEEE Trans.on Signal Processing， 2004， 52（9）： 2407-2423.

［19］ VOROBYOV S A， CHEN H H， GERSHMAN A B. On the relationship between robust minimum variance beamformers with probabilistic and worst-case distortionless response constraints［J］. IEEE Trans.on Signal Processing， 2008， 56（11）： 5719-5724.

［20］ JIANG X， ZENG W J， YASOTHARAN A， et al. Robust beamforming by linear programming［J］. IEEE Trans.on Signal Processing， 2014， 62（7）： 1834-1849.

［21］ ZHUANG J， MANIKAS A. Interference cancellation beamforming robust to pointing errors［J］. IET Signal Processing， 2013， 7（2）： 120-127.

［22］ RUAN H， DE LAMARE R C. Robust adaptive beamforming using a low-complexity shrinkage-based mismatch estimation algorithm［J］. IEEE Signal Processing Letters， 2014， 21（1）： 60-64.

［23］ GU Y J， LESHEM A. Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation［J］. IEEE Trans.on Signal Processing， 2012， 60（7）： 3881-3885.

［24］ HUANG L， ZHANG J， XU X， et al. Robust adaptive beamforming with a novel interference-plus noise covariance matrix reconstruction method［J］. IEEE Trans.on Signal Processing， 2015， 63（7）： 1643-1650.

［25］ GU Y J， GOODMAN N A， HONG S， et al. Robust adaptive beamforming based on interference covariance matrix sparse reconstruction［J］. Signal Processing， 2014， 96（B）： 375-381.

［26］ SHEN F F， CHEN F F， SONG J Y. Robust adaptive beamforming based on steering vector estimation and covariance matrix reconstruction［J］. IEEE Communication Letters， 2015， 19（9）： 1636-1639.

［27］ ZHANG Z T， LIU W， LENG W，" et al. Interference-plus-noise covariance matrix reconstruction via spatial power spectrum sampling for robust adaptive beamforming［J］. IEEE Signal Processing Letters， 2016， 23（1）： 121-125.

［28］ YUAN X L， GAN L. Robust adaptive beamforming via a novel subspace method for interference covariance matrix reconstruction［J］. Signal Processing， 2017， 130： 233-242.

［29］ ZHENG Z， YANG Y， WANG W Q， et al. Robust adaptive beamforming via simplified interference power estimation［J］. IEEE Trans.on Aerospace and Electronic Systems， 2019， 55（6）： 3139-3152.

［30］ ABEIDA H， ZHANG Q L， LI J. Iterative sparse asymptotic minimum variance based approaches for array processing［J］. IEEE Trans.on Signal Processing， 2013， 61（3）： 933-944.

［31］ ABEIDA H， DELMAS J. Efficiency of subspace-based DOA estimators［J］. Signal Processing， 2007， 87： 2075-2084.

［32］ 章平亮， 張建秋. 一般性廣義噪聲協方差矩陣自適應迭代譜估計［J］. 系統工程與電子技術， 2013， 35（10）： 2037-2043.

ZHANG P L， ZHANG J Q. Adaptive iterative nonparametric spectral estimation method based on generalized noise covariance［J］. Systems Engineering and Electronics， 2013， 35（10）： 2037-2043.

［33］ 張賢達. 矩陣分析與應用［M］. 北京： 清華大學出版社， 2004.

ZHANG X D. Matrix analysis and application［M］. Beijing： Tsinghua University Press， 2004.

作者簡介

盧文龍（1998—），男，碩士研究生，主要研究方向為陣列信號處理。

李 旦（1982—），男，副教授，博士，主要研究方向為信號處理及應用。

畢權楊（1995—），男，博士研究生，主要研究方向為信號處理。

張建秋（1962—），男，教授，博士，主要研究方向為信號處理及應用。