新型迅捷彈箭多源力組合控制方法

摘 要：

為大幅度提高導彈的超大角度機動能力，提出一種新型迅捷彈箭多源力組合控制方法。首先通過在傳統直接力/氣動力復合控制敏捷導彈尾部加裝一類柔性可控傘，設計一種新型彈箭構型，然后基于合理假設將柔性可控傘簡化為作用在敏捷導彈尾部的可控柔性力，并給出可控柔性力大小、方向、驅動機構動態響應特性的量化描述方法，進而建立鉛垂平面內引入可控柔性力的動力學模型，最后針對強耦合、強不確定性、快時變性、強非線性的多輸入多輸出系統，設計柔性力/直接力/氣動力復合控制律，實現了新型彈箭的迅捷轉向。通過仿真驗證了所提方法的合理性和有效性，并與傳統敏捷導彈進行仿真對比，驗證了所提方法有利于提高超大角度機動能力。

關鍵詞：

導彈; 敏捷轉彎; 柔性可控傘; 可控柔性力; 滑模控制; 擴張狀態觀測器

中圖分類號：

V 249.1; TJ 765.2

文獻標志碼： A"" DOI：10.12305/j.issn.1001-506X.2024.05.26

Multi-source force combined control method for novel agile projectiles

ZHAO Xinyun， YU Jianqiao*

（School of Aerospace Engineering， Beijing Institute of Technology， Beijing 100081， China）

Abstract：

A multi-source force control method for novel agile projectiles is proposed to improve the large angle maneuverability of the missiles. Firstly， the geometric configuration of the novel agile projectiles is designed by adding a type of flexible and controllable parachute to the tail of traditional reaction-jet and aerodynamic compound control agile missiles. Then， based on reasonable assumptions， the flexible and controllable parachute is simplified as a controllable flexible force acting on the tail of agile missiles. A quantitative description method for the magnitude， direction， and dynamic response characteristics of the controllable flexible force is provided. Furthermore， a dynamic model introducing controllable flexible force in the vertical plane is established. Finally， for the multiple input multiple output system with strong coupling/strong uncertainty/fast time variability， and strong nonlinearity， the flexible force， reaction-jet and aerodynamic compound control law is designed to achieve the agile turn of the novel projectiles. The rationality and effectiveness of the proposed method is verified through simulation， and compared with traditional agile missiles， it is verified that the proposed method is beneficial for improving the large angle maneuverability.

Keywords：

missile; agile turn; flexible and controllable parachute; controllable flexible force; sliding mode control; extended state observer （ESB）

0 引 言

在現代化戰爭中，各種作戰場景往往都需要導彈具有超大角度機動能力來實現對目標的有效攻擊，如空空導彈攻擊位于載機后半球的目標，防空導彈在制導末端對機動逃逸目標進行有效攔截，反艦導彈受干擾脫靶后進行二次攻擊，戰術導彈攻擊密集障礙物后的隱匿目標等。導彈在進行上述快速大角度機動的過程中，攻角往往會超過90°［1］。導彈以大攻角飛行時會進入嚴重的失速階段，只依靠氣動舵不足以改變其運動狀態，通常引入直接力裝置或推力矢量裝置進行復合控制來實現導彈的敏捷轉彎。

大攻角飛行時導彈的動力學模型不可線性化，且氣動力具有極大的不確定性。敏捷導彈強非線性、快時變性、強不確定性的特點為控制器的設計帶來諸多復雜的難點。文獻［2］建立了引入直接力后的小攻角動力學模型和大攻角動力學模型，基于線性滑模設計了直接力/氣動力復合控制律，實現了縱向平面內的敏捷轉彎。文獻［3］在分析直接力有限約束集的基礎上，基于模型預測與自抗擾控制設計了復合控制律。文獻［4］基于神經網絡動態逆生成攻角指令，并設計了線性滑模控制器，實現了對后方導彈的大角度機動攔截。以上文獻均側重于復合控制系統的實現問題和控制分配問題。

文獻［5］設計了分段線性滑模控制律，改善了線性滑模控制的性能，提高了復合控制效率。文獻［6］設計了考慮輸入飽和與有界干擾的積分滑模控制器，并基于動態控制分配方法獲得了氣動舵和直接力裝置的實際指令。文獻［7］設計了一種固定時間收斂的雙冪次滑模控制器，來獲得建立導彈過載所需要的虛擬控制力矩，并采用動態控制分配方法將其分解到氣動舵和直接力裝置。文獻［8］基于滑模控制設計了俯仰平面的控制律，在不帶增益調度的條件下，對參數變化造成的有界不確定性下的系統魯棒性進行了分析驗證。文獻［9］針對大攻角下氣動力的強不確定性和系統參數的快時變性，基于反步法和H∞方法設計了具有較強魯棒性的控制器。文獻［10-11］兼顧收斂速度和抗干擾特性，設計了新型非奇異終端滑模控制器。以上文獻均側重于跟蹤誤差收斂速度問題和不確定性的動態補償問題。

圓形傘雖然廣泛應用于航空、航天和武器工業領域［12-28］，但是主要是借助圓形傘對導彈/物體的減速、減旋作用來實現系統的軌跡規劃、姿態穩定。對傘物/傘彈系統的研究主要集中在無控系統的動力學建模［14-17］、表觀質量對系統穩定性的影響［18-21］，以及初始狀態、各種干擾對無控系統軌跡的影響［22-24］。當考慮傘的主動控制時，物體/導彈一般只考慮其受到的重力，用以傘為主體建立的單剛體模型來描述有控傘物/傘彈系統的運動狀態［25-28］。未見有將傘應用于彈箭大角度機動領域的研究和成果。

與以往敏捷轉彎領域學者從控制方法上尋求創新、追求控制器的良好性能不同，本文為進一步大幅度提高導彈的超大角度機動能力，通過在傳統直接力/氣動力復合控制敏捷導彈尾部加裝一類柔性可控傘，設計了一種新型迅捷彈箭，通過引入新型控制方式來尋求提高彈箭敏捷性能的可能性。

與現有傘物/傘彈領域學者側重于研究系統的軌跡規劃、姿態穩定不同，本文聚焦于研究新型迅捷彈箭的超大角度機動能力，基于合理假設將柔性可控傘簡化為作用在敏捷導彈尾部的可控柔性力，并給出可控柔性力大小、方向、驅動機構動態響應特性的量化描述方法，進而建立鉛垂平面內引入可控柔性力的動力學模型。然后，以此為基礎，針對強耦合、強不確定性、快時變性、強非線性的多輸入多輸出系統，基于模糊邏輯建立柔性力大小和方向的關系;基于虛擬控制的思想，將系統分解成彈道傾角通道子系統和俯仰角通道子系統，分別設計滑模控制器得到兩個子系統的虛擬控制量;通過反推得到系統控制驅動機構的實際控制量，并利用擴張狀態觀測器估計系統的總擾動，消除內外擾動對系統造成的負面影響，抑制了抖振，并證明了所提方法的有限時間收斂特性。通過仿真驗證了所提方法的合理性和有效性，并與傳統敏捷導彈進行仿真對比，驗證了所提方法有利于提高敏捷轉彎性能。

1 新型迅捷彈箭動力學建模

1.1 新型迅捷彈箭幾何構型及其敏捷轉彎過程

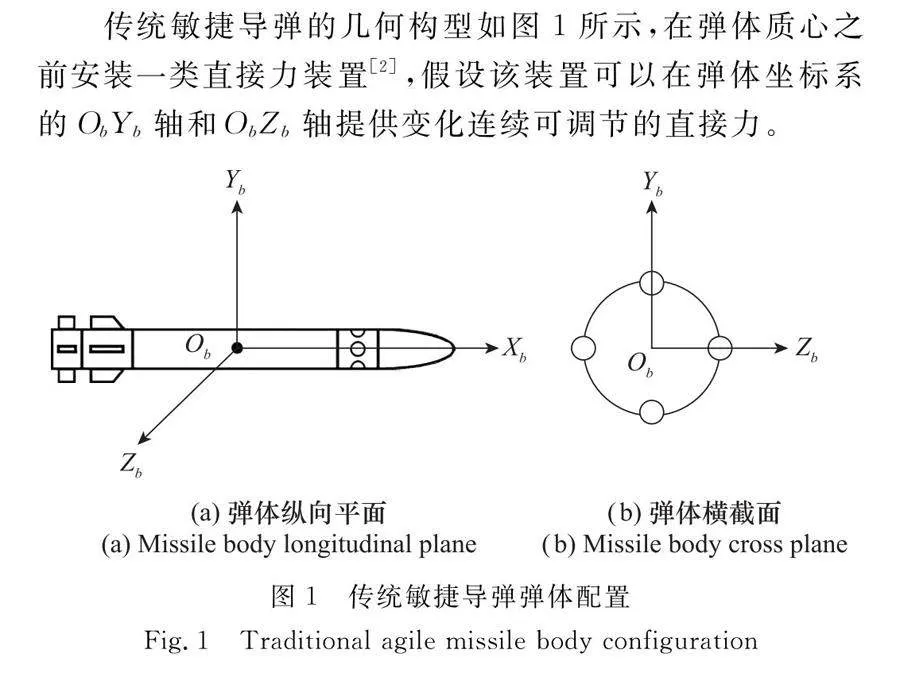
傳統敏捷導彈的幾何構型如圖1所示，在彈體質心之前安裝一類直接力裝置［2］，假設該裝置可以在彈體坐標系的ObYb軸和ObZb軸提供變化連續可調節的直接力。

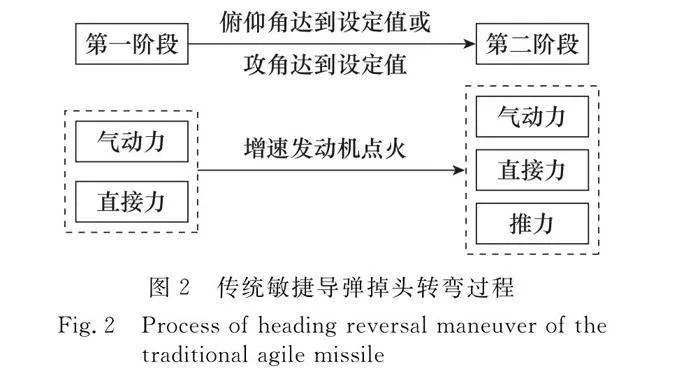
傳統敏捷轉彎過程如圖2所示。第一階段，導彈由直接力/氣動力復合控制，當俯仰角或攻角達到預先設定值時，增速發動機點火。進入第二階段，其后導彈仍由直接力/氣動力復合控制，增速發動機提供的推力不可控制。

為進一步大幅度提高導彈的超大角度機動能力，設計一種新型迅捷彈箭，其幾何構型如圖3所示，考慮一類柔性可控傘，安裝在傳統直接力/氣動力復合控制敏捷導彈的尾部。為與常規圓形傘相區別，將能為導彈提供一定可用法向過載的傘，命名為柔性可控傘，為與傳統敏捷導彈及其敏捷轉彎相區別，將這一類柔性力/直接力/氣動力復合控制的具備超大角度機動飛行能力的新型彈箭，命名為迅捷彈箭，將迅捷彈箭在某一飛行時間段內完成超大角度機動掉頭轉向的過程，命名為迅捷轉向。

新型迅捷彈箭敏捷轉彎過程如圖4所示。第一階段，導彈由柔性力/直接力/氣動力復合控制，在俯仰角達到預先設定值時，拋掉柔性可控傘。進入第二階段，其后導彈由直接力/氣動力復合控制，當攻角達到預先設定值時，增速發動機點火，進入第三階段，其后導彈仍由直接力/氣動力復合控制，增速發動機提供的推力不可控制。

與傳統敏捷轉彎相比，新型迅捷轉向增加了柔性力/直接力/氣動力復合控制階段;增速發動機點火的條件只能以攻角為參考，而不能以俯仰角為參考;設置第二階段的目的主要是創造點火條件，其時間較第一、三階段短。引入第一階段的作用以及合適的點火條件將在建立動力學模型后進一步詳細討論。

可建立多體動力學模型研究柔性可控傘-敏捷導彈系統整體的運動特性，但本文更關心的是大幅度提高導彈的超大角度機動能力需要呈何種變化規律的柔性力，因此將傘的動力學特性抽象出來，將柔性可控傘簡化為一個大小和方向在允許范圍內變化的、作用點在導彈尾部截面中心的一個可控柔性力。研究大幅度提高導彈的超大角度機動能力需要呈何種變化規律的柔性力也可對適用于敏捷轉彎的柔性可控傘的設計提供指標要求和參考。

在以往圓形傘的應用中，無控圓形傘產生的力對與其連接的物/彈的作用效果主要是減速，此時可近似認為圓形傘產生的力是沿著物/彈速度反方向的阻力。考慮到以提高軌跡精度為目的的可控圓形傘，文獻［25-28］指出繩索收放引起傘衣變形進而產生操縱力，其大小與繩索收放長度相關，傘受到的力為傘衣未變形時受到的無控力與變形后產生的操縱力之和。因此，考慮到本文通過加裝柔性可控傘提高導彈可用法向過載的目的，近似將柔性可控傘未變形時產生的對導彈起減速作用效果的力，與通過繩索收放變形后產生的操縱力之和，等效為柔性可控傘產生的與導彈速度反向延長線的夾角不超過ηmax的一個可控柔性力，且ηmax的值與柔性可控傘通過繩索收放產生操縱力的能力相關，初步設計中，可認為ηmax=5°。

1.2 新型迅捷彈箭動力學模型

文獻［2］以40°攻角為界限將敏捷轉彎過程分為小攻角階段和大攻角階段，由于DATCOM軟件不適用于計算大攻角下的氣動參數，常采用分析方法進行估計，文獻［2］將導彈假設為圓柱體，構造了攻角、雷諾數和馬赫數的函數來求解大攻角下的氣動參數。

新型迅捷彈箭較傳統敏捷導彈增添了所述的可控柔性力，其受力分析如圖5所示，建立新型迅捷彈箭的動力學模型為

時間與能量消耗如表2所示，新型迅捷彈箭轉彎時間較傳統的縮短14.21%，直接力裝置能量消耗較傳統的增加17.33%，增速發動機的能量消耗較傳統減少21.02%，總的能量消耗較傳統的減少14.53%。

彈道曲線如圖7所示，新型迅捷彈箭和傳統敏捷導彈均能實現180°掉頭轉彎，且新型迅捷彈箭的轉彎半徑更小。俯仰角、攻角和彈道傾角曲線如圖8所示，新型迅捷彈箭和傳統敏捷導彈均快速建立起俯仰角和攻角，當俯仰角趨于穩定時攻角逐漸收斂。新型迅捷彈箭第一階段和傳統敏捷導彈第一階段建立起的俯仰角大致相等，而新型迅捷彈箭也建立起較大的彈道傾角，當拋掉柔性可控傘進入第二階段后，彈道傾角幾乎不變，攻角在直接力/氣動力復合控制下快速接近90°，為增速發動機創造合適的點火條件。

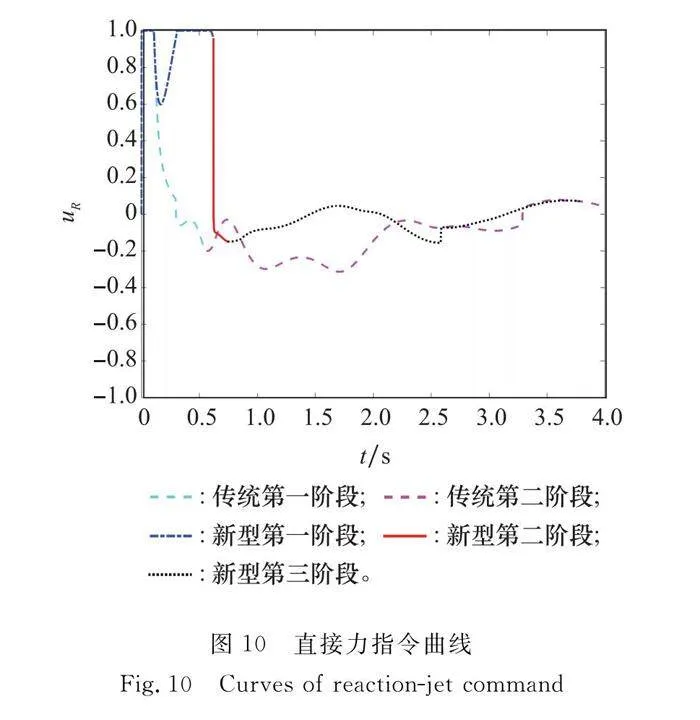
俯仰角角速度如圖9所示，新型迅捷彈箭和傳統敏捷導彈在建立俯仰角的速度上幾乎相同。直接力指令曲線如圖10所示，新型迅捷彈箭第一階段的直接力消耗要大于傳統敏捷導彈的。這是因為柔性力雖然起到了增大彈道傾角的作用，但是同時也產生了阻礙俯仰角增大的力矩，而為保持俯仰角速度不變，需要更大的直接力產生控制力矩抵消掉柔性力的負面影響，所以直接力裝置在第一階段的消耗增大。

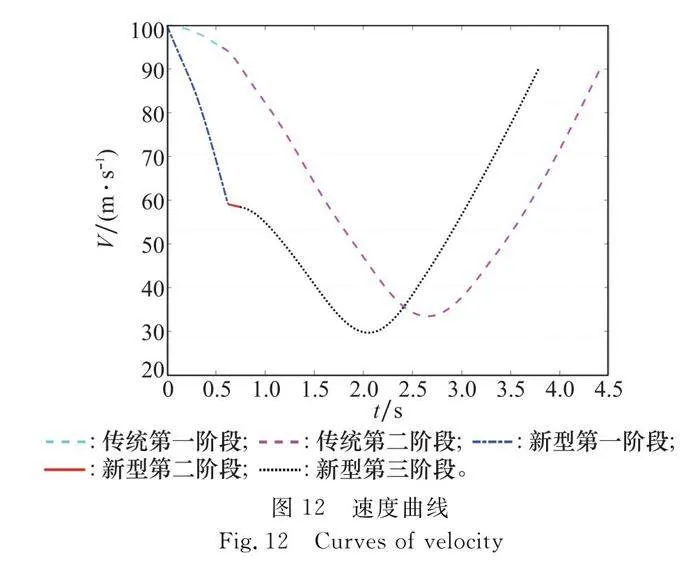
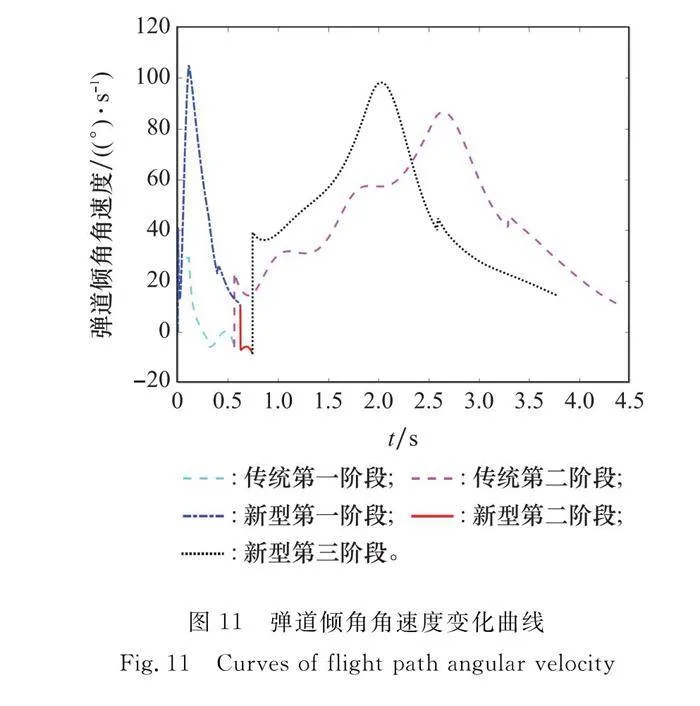
彈道傾角角速度曲線如圖11所示，新型迅捷彈箭第一階段的彈道傾角角速度遠大于傳統敏捷導彈的，這得益于柔性力的引入。當拋掉柔性可控傘進入到第二階段時，彈道傾角角速度立刻減小到零左右。當增速發動機點火后，新型迅捷彈箭進入第三階段，傳統敏捷導彈進入第二階段，增速發動機推力在垂直速度方向上的分量使得彈道傾角角速度處于較大的值。速度曲線如圖12所示，由于柔性力的減速作用，使得新型迅捷彈箭在第一階段的減小量遠遠大于傳統敏捷導彈的。新型迅捷彈箭和傳統敏捷導彈的點火條件都是攻角達到90°，但是由于新型迅捷彈箭點火增速發動機時的速度小于傳統敏捷導彈的（由增速發動機產生的彈道傾角角速度為Tsin α/（mV），使得新型迅捷彈箭的彈道傾角角速度在增速發動機點火后的很長一段時間內都大幅度高于傳統敏捷導彈的，這有利于提高敏捷轉彎性能。

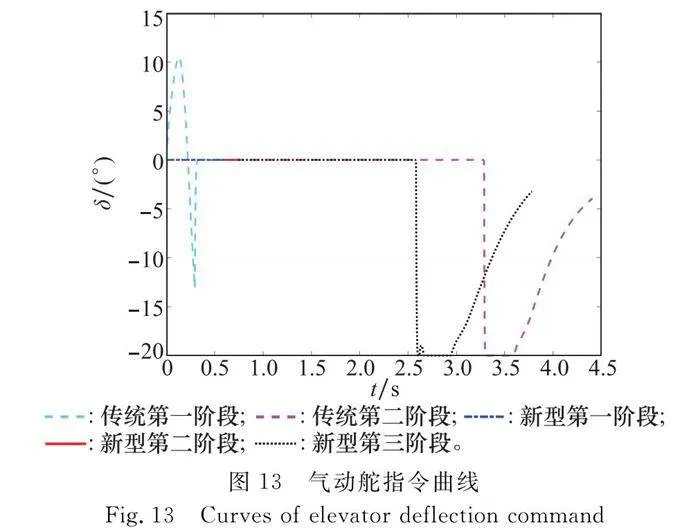
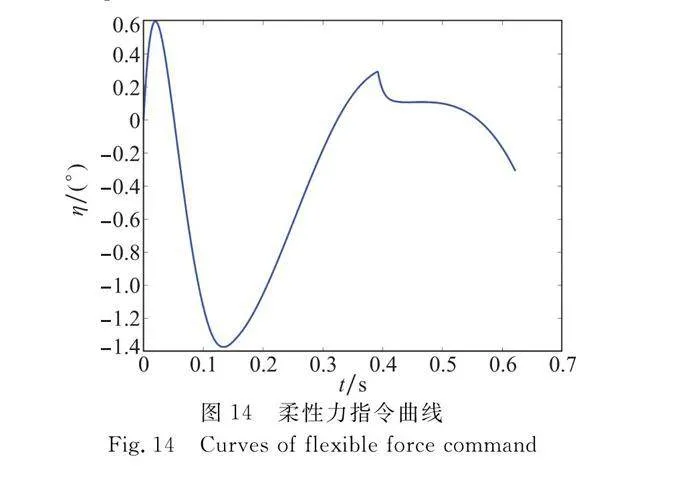
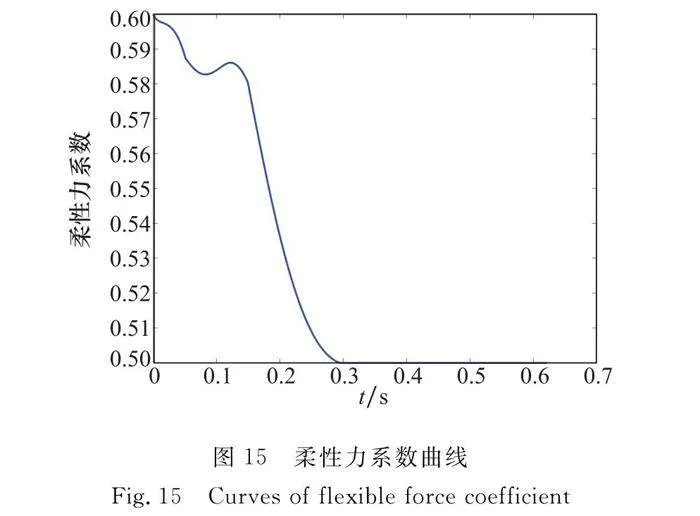
氣動舵指令曲線如圖13所示，新型迅捷彈箭第三階段和傳統敏捷導彈第二階段氣動舵都出現打滿的狀態。新型迅捷彈箭在姿態穩定后，攻角快速收斂，先于傳統敏捷導彈降到40°之下，使氣動舵率先從失效狀態恢復，有利于提高最后一階段的敏捷轉彎性能。柔性力指令曲線如圖14所示，柔性力指令在初始很短的時間內是正值，此時對建立俯仰角起正向作用，而后快速負向增大，使導彈快速建立彈道傾角，當彈道傾角逐漸趨于其預期值時，柔性力指令大小逐漸減小。柔性力系數曲線如圖15所示，當彈道傾角跟蹤誤差逐漸減小時柔性力系數也逐漸減小，當柔性力指令大小快速增大時柔性力系數小幅度增大來減緩柔性力指令增大的趨勢。

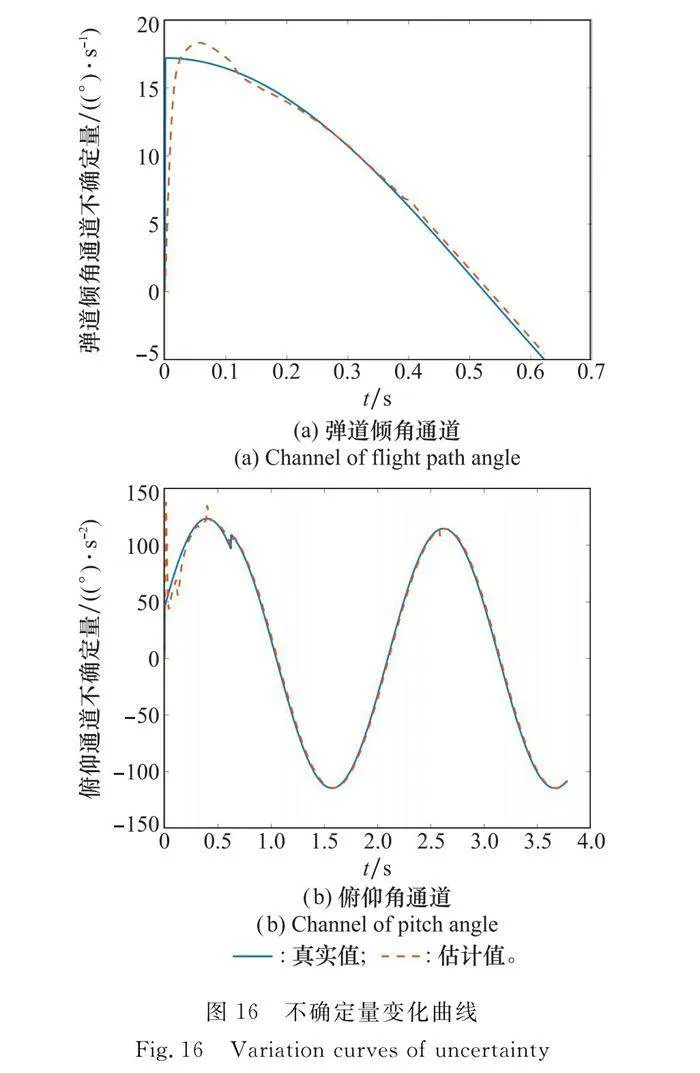
不確定量變化及其估計值曲線如圖16所示，擴張狀態觀測器精確實時地估計了彈道傾角通道和俯仰角通道擾動的大小。

4 結 論

本文為提高導彈的超大角度機動能力，設計了一種新型迅捷彈箭，提出一種多源力組合控制方法，具有以下優勢：

（1） 相較于傳統敏捷導彈，新型迅捷彈箭的轉彎半徑更小，并且大幅縮小了達到與末制導交班所需狀態的時間。

（2） 相較于傳統敏捷導彈，新型迅捷彈箭完成敏捷轉彎，大幅減小了所消耗的能量，節約了成本，具有潛在的工程應用價值。

（3） 新型迅捷彈箭在不影響俯仰角跟蹤效果的同時，實現了對彈道傾角的跟蹤控制。

（4） 提出的多源力組合控制方法能保證系統在未建模動態、內部參數攝動、外界干擾等影響下仍具有較強的魯棒性和較高的跟蹤精度。

（5） 本文從動力學與控制角度初步論證了新型迅捷彈箭理論方案的可行性，研究了大幅度提高導彈的超大角度機動能力需要呈何種變化規律的柔性力，可為后續氣動分系統深入研究柔性可控傘的作用機理，設計出適用于敏捷轉彎的柔性可控傘提供指標要求和參考。

參考文獻

［1］ GONG X P， CHEN W C， CHEN Z Y. All-aspect guidance law for agile missiles based on deep reinforcement learning［J］. Aerospace Science and Technology， 2022， 127： 107677.

［2］ THUKRAL A， INNOCENTI M. A sliding mode missile pitch autopilot synthesis for high angle of attack maneuvering［J］. IEEE Trans.on Control Systems Technology， 1998， 6（3）： 359-371.

［3］ 畢永濤， 王宇航， 姚郁. 直/氣復合控制導彈的模型預測和自抗擾姿態控制設計［J］. 宇航學報， 2015， 36（12）： 1373-1383.

BI Y T， WANG Y H， YAO Y. Attitude control design of missiles with dual control based on model predictive control and active disturbance rejection control［J］. Journal of Astronautics， 2015， 36（12）： 1373-1383.

［4］ MA Y Y， GUO J， TANG S J. High angle of attack command generation technique and tracking control for agile missiles［J］. Aerospace Science and Technology， 2015， 45： 324-334.

［5］ 霍鑫， 彭繼平， 馬克茂， 等. 空空導彈敏捷轉彎的分段線性滑模控制設計［J］. 系統工程與電子技術， 2017， 39（10）： 2278-2284.

HUO X， PENG J P， MA K M， et al. Piecewise linear sliding mode control design for agile turn of air-to-air missile［J］. Systems Engineering and Electronics， 2017， 39（10）： 2278-2284.

［6］ GUO Y， GUO J H， LIU X， et al. Finite-time blended control for air-to-air missile with lateral thrusters and aerodynamic surfaces［J］. Aerospace Science and Technology， 2020， 97： 105638.

［7］ 劉祥， 李愛軍， 郭永， 等. 固定時間收斂的空空導彈直接力/氣動力復合控制［J］. 哈爾濱工業大學學報， 2019， 51（9）： 29-34， 42.

LIU X， LI A J， GUO Y， et al. Fixed-time convergence blended control for air-to-air missile with lateral thrusters and aerodynamic force［J］. Journal of Harbin Institute of Technology， 2019， 51（9）： 29-34， 42.

［8］ KIM Y， KIM B S. Pitch autopilot design for agile missiles with uncertain aerodynamic coefficients［J］. IEEE Trans.on Aerospace and Electronic Systems， 2013， 49（2）： 907-914.

［9］ MAHMOOD A， KIM Y， PARK J. Robust H∞ autopilot design for agile missile with time-varying parameters［J］. IEEE Trans.on Aerospace and Electronic Systems， 2014， 50（4）： 3082-3089.

［10］ 趙新運， 于劍橋. 導彈敏捷轉彎段的新型非奇異終端滑模控制［J］. 宇航學報， 2022， 43（4）： 454-464.

ZHAO X Y， YU J Q. Novel non-singular terminal sliding mode control for missile’s agile turn［J］. Journal of Astronautics， 2022， 43（4）： 454-464.

［11］ 李政， 于劍橋， 趙新運. 空空導彈敏捷轉彎固定時間收斂滑模控制［J］. 航空學報， 2023， 44（8）： 327262.

LI Z， YU J Q， ZHAO X Y. Fixed-time convergent sliding mode control for agile turn of air-to-air missiles［J］. Acta Aeronautica et Astronautica Sinica， 2023， 44（8）： 327262.

［12］ 李健， 房冠輝， 呂智慧， 等. 天問一號火星探測器傘系減速分系統設計與驗證［J］. 中國科學： 技術科學， 2022， 52（2）： 264-277.

LI J， FANG G H， LYU Z H， et al. Design and verification of parachute deceleration subsystem of Tianwen-1 Mars probe［J］. Scientia Sinica Technologica， 2022， 52（2）： 264-277.

［13］ 董捷， 饒煒， 孫澤洲， 等. 火星傘降段多體動力學特性分析與安全設計研究［J］. 中國科學： 技術科學， 2022， 52（8）： 1175-1185.

DONG J， RAO W， SUN Z Z， et al. Multibody dynamics cha-racteristics analysis and safety design research of the Mars para-chute descent process［J］. Scientia Sinica Technologica， 2022， 52（8）： 1175-1185.

［14］ WHITE F M， WOLF D F. A theory of three-dimensional parachute dynamic stability［J］. Journal of Aircraft， 1968， 5（1）： 86-92.

［15］ WOLF D F. Dynamic stability of a nonrigid parachute and payload system［J］. Journal of Aircraft， 1971， 8（8）： 603-609.

［16］ DOHERR K F， SCHILLING H. Nine-degree-of-freedom simulation of rotating parachute systems［J］. Journal of Aircraft， 1992， 29（5）： 774-781.

［17］ XING X J， FENG L， CHEN M P， et al. Modeling and research of a multi-stage parachute system for the booster reco-very［J］. Proceedings of the Institution of Mechanical Engineers Part G： Journal of Aerospace Engineering， 2023， 237（5）： 1135-1157.

［18］ COCKRELL D J， DOHERR K F. Preliminary consideration of parameter identification analysis from parachute aerodynamic flight test data［R］. San Diego： AIAA， 1981.

［19］ EATON J A. Added mass and the dynamics stability of parachutes［J］. Journal of Aircraft， 1982， 19（5）： 414-416.

［20］ EATON J A. Added fluid mass and the equations of motion of a parachute［J］. Aeronautical Quarterly， 1983， 34（3）： 226-242.

［21］ GINN J M， CLARK I G， BRAUN R D. Parachute dynamics stability and the effects of apparent inertial［R］. Atlanta： AIAA， 2014.

［22］ CAO Y H， WEI N. Flight trajectory simulation and aerodynamic parameter identification of large-scale parachute［J］. International Journal of Aerospace Engineering， 2020， 2020： 5603169.

［23］ GAO X L， ZHANG Q B， TANG Q G. Parachute dynamics and perturbation analysis of precision airdrop system［J］. Chinese Journal of Aeronautics， 2016， 29（3）： 596-607.

［24］ PHAM T D， NGUYEN A T， LE V D， et al. Trajectory analyses of uncontrolled circular parachutes in random spatial wind fields［J］. Journal of Mechanical Science and Technology， 2022， 36（8）： 3825-3835.

［25］ DOBROKHODOV V， YAKIMENKO O， JUNGE C. Six-degree-of-freedom model of a controlled circular parachute［R］. Monterey： AIAA， 2002.

［26］ FIELDS T D， LACOMBE J C， WANG E L. Autonomous guidance of a circular parachute using descent rate control［J］. Journal of Guidance， Control， and Dynamics， 2012， 35（4）： 1367-1370.

［27］ FIELDS T D， BASORE N. Reversible control line reefing system for circular parachutes［R］. Daytona Beach： AIAA， 2015.

［28］ FIELDS T D. Evaluation of control line reefing systems for circular parachute［J］. Journal of Aircraft， 2016， 53（3）： 855-859.

［29］ 錢杏芳， 林瑞雄， 趙亞男. 導彈飛行力學［M］. 北京： 北京理工大學出版社， 2000.

QIAN X F， LIN R X， ZHAO Y N. Missile flight dynamics［M］. Beijing： Beijing Institute of Technology Press， 2000.

［30］ HAN J Q. From PID to active disturbance rejection control［J］. IEEE Trans.on Industrial Electronics， 2009， 56（3）： 900-906.

［31］ XIONG S F， WANG W H， LIU X D， et al. A novel extended state observer［J］.ISA Transactions， 2015， 58： 309-317.

［32］ UTKIN V I. Control systems of variable structure［M］. New York： Wiley， 1976.

［33］ 高為炳. 變結構控制的理論及設計方法［M］. 北京： 科學出版社， 1996.

GAO W B. Theory and design method for variable sliding mode control［M］. Beijing： Science Press， 1996.

［34］ DING S H， MEI K Q， YU X H. Adaptive second-order sliding mode control： a Lyapunov approach［J］. IEEE Trans.on Automatic Control， 2022， 67（10）： 5392-5399.

［35］ CAO X Q， GE Q X， ZHU J Q， et al. Improved sliding mode traction control combined sliding mode disturbance observer strategy for high-speed Maglev train［J］. IEEE Trans.on Power Electronics， 2023， 38（1）： 827-838.

［36］ HOU H Z， YU X H， FU Z. Sliding mode control of networked control systems： an auxiliary matrices-based approach［J］. IEEE Trans.on Automatic Control， 2022， 67（7）： 3574-3581.

［37］ FENG Y， YU X H， MAN Z H. Non-singular terminal sliding mode control of rigid manipulators［J］. Automatica， 2002， 38（12）： 2159-2167.

［38］ 梅紅， 王勇. 快速收斂的機器人滑模變結構控制［J］. 信息與控制， 2009， 38（5）： 552-557.

MEI H， WANG Y. Fast convergent sliding mode variable structure control of robot［J］. Information and Control， 2009， 38（5）： 552-557.

作者簡介

趙新運（1998—），男，碩士研究生，主要研究方向為飛行器總體設計、飛行力學與控制。

于劍橋（1972—），男，教授，博士，主要研究方向為飛行器總體設計、飛行力學與控制。