基于多精度規劃窗口的無人機航跡規劃方法研究

摘 要：

航跡規劃是無人機（unmanned aerial vehicle， UAV）任務規劃系統的核心部分之一，其主要任務是結合戰場環境等約束條件，尋找一條安全系數高、滿足任務需求且飛行代價小的UAV最優飛行航跡。基于現有蟻群優化（ant colony optimization， ACO）算法，在其并行能力基礎上提出一種多精度規劃窗口方法。該方法在初始航跡基礎上，進一步針對局部飛行環境特點，自動配置局部規劃窗口、規劃精度和規劃參數，并行地開展多精度窗口航跡調整，可在較短時間內優化出一條適應戰場環境的飛行航跡。仿真分析表明，不同戰場環境下所需的算法參數配置、規劃精度各有不同，通過多精度規劃窗口的優化與調整，最終飛行航跡可適應不同戰場環境，且具備較好的規劃效率與精度。

關鍵詞：

無人機; 航跡規劃; 蟻群優化算法; 多精度優化; 優化算法

中圖分類號：

TP 391

文獻標志碼： A""" DOI：10.12305/j.issn.1001-506X.2024.05.29

Research on UAV path planning method based on the

multi-precision planning windows

YU Jing， WU Xiaojun， JIANG Anlin， YONG Enmi*

（Computational Aerodynamics Institute， China Aerodynamics Research and Development Center， Mianyang 621000， China）

Abstract：

Path planning plays a significant role on the unmanned aerial vehicle （UAV） mission planning. It is aiming at finding a safest UAV trajectory of optimal flying cost， considering the battlefield environment and other mission requirements. Based on the parallel ability of ant colony optimization （ACO） algorithm， a multi-precision planning window method is proposed. Based on the initial trajectory， it can automatically set multiple local planning windows with specifical planning precisions and optimization parameters， and then parallel path modification in a short time. Simulation analysis shows that the algorithm parameters configuration and planning accuracy are different in different battlefield environments. Through the optimization and adjustment of multi-precision planning window， the final flight path can adapt to different battlefield environment， and has better planning efficiency and accuracy.

Keywords：

unmanned aerial vehicle （UAV）; path planning; ant colony optimization （ACO） algorithm; multi-precision optimization; optimization algorithm

0 引 言

無人作戰飛機具有低成本、隱身性能好、零傷亡、持續作戰能力強等優勢，極大地提高了高風險目標突防、縱深目標攻擊等能力［1］。航跡規劃是無人作戰飛機任務規劃系統的核心部分之一，其任務是在任務分配的基礎上，結合戰場環境、飛行能力等一系列約束條件，盡量規避威脅，為無人作戰飛機找到盡可能優的滿足任務需求的可行飛行航跡。航跡規劃的優劣，決定了無人機能否在復雜多變的環境下順利完成任務，并使得飛行代價最小。

目前，國內外對無人機的航跡規劃研究已有大量研究成果［2-3］。航跡規劃算法包括傳統航跡規劃算法，如人工勢場法、A*算法、Dijkstra算法等。人工勢場法規劃速度快、實時性好，但是對復雜環境適應性不足，容易陷入局部最優［4］。A*算法［2，5］本質上是廣度優先搜索，搜索性能好，準確度高，但當搜索節點增多時，其搜索效率低的問題突出，且實時性差，更適用于靜態優化。Dijkstra算法是經典的最短路徑算法，其優點是算法簡單、優化速度快，但對復雜環境和多約束問題適應性不足。隨著人工智能技術的不斷發展，大量智能算法被應用于無人機的航跡規劃，如：蟻群優化（ant colony optimation， ACO）算法、神經網絡法、粒子群優化算法、遺傳算法、模擬退火算法等。智能優化算法的共同特點是，均基于概率原則進行搜索，方法靈活，理論上可以得出全局最優解。但在具體應用中，基于具體的問題和算法設計，不同算法又會表現出各自問題。文獻［6］對比了粒子群優化算法和遺傳算法在無人機航跡規劃中的優化效果，指出遺傳算法存在收斂速度慢、算法參數敏感度高等問題，粒子群優化算法存在早熟收斂等問題。文獻［7］指出，模擬退火算法存在對初始解依賴性強、且容易陷入局部最優的問題。神經網絡算法的核心在于訓練和學習，主要適用于飛行環境已知，同一區域需要多次搜索的情況，因此對于戰場時變環境，神經網絡算法還需進一步探討［8］。ACO算法是較早應用于航跡規劃的智能優化算法之一［9-12］，其模擬蟻群覓食行為，通過信息素的作用使整個蟻群具有高自組織性、信息交換和反饋機制，并最終以螞蟻行走路徑表示優化問題的可行解。ACO算法因其具備并行處理機制、魯棒性強、全局搜索能力強等優勢，在航跡規劃中備受關注，但其亦有易于陷入局部最優、收斂慢、參數多等問題［13］。針對不同算法的局限性，諸多研究者針對規劃問題的具體特點，有側重點地進行了算法改進或是混合算法的航跡規劃應用研究［14-21］。

快速、高精度規劃是航跡規劃一直孜孜以求的目標。本文基于ACO算法魯棒性好、可并行、全局搜索能力強等優勢，針對其存在的規劃精度制約收斂速度、整體參數調整繁雜等問題，開展基于ACO算法的改進航跡規劃方法研究。通過提出一種多精度規劃窗口方法，在初始航跡基礎上，進一步針對局部飛行環境特點，自動配置局部規劃窗口、規劃精度和規劃參數，并行地開展多精度窗口航跡調整，可在較短時間內優化出一條適應戰場環境的飛行航跡，可提高現有ACO航跡規劃算法的效率和規劃精度。

本文組織如下：第1節對本文研究問題進行描述，第2節對戰場環境中的威脅模型進行描述，第3節給出本文提出的航跡規劃模型，第4節給出基于多精度規劃窗口的航跡規劃算法，第5節通過仿真驗證算法的有效性，第6節進行全文總結。

1 問題描述

本文研究的無人機航跡規劃，就是根據無人機的具體任務需求，在給定的規劃空間里，找到一條可以適應地形限制、規避雷達/防空火力威脅、規避惡劣氣象環境、且滿足一系列機動特性約束的，從起始點到目標點的相對最優路徑，使得無人機飛行航程盡可能短，安全系數盡可能高。

無人機的實際飛行過程中包含了起飛、爬升、巡航、下降、著陸等階段，本文的航跡規劃，特指巡航段，且不考慮返程航跡。本文假設，無人機在巡航過程中高度和速度基本保持不變，則本文的航跡規劃問題實質上是一個二維平面的路徑規劃問題［22］，如圖1所示。

2 威脅模型

在無人機飛行過程中，會遇到各種各樣的威脅，無人機需要通過調整航向等飛行姿態規避威脅區域，以安全到達目標點執行預定任務（見圖2）。本文主要考慮：① 雷達威脅：防止被探測到并跟蹤鎖定;② 火力威脅：防止被擊落;③ 地形/氣象/禁飛區威脅：防止飛行過程中與山峰碰撞或低于安全高度而墜地，防止誤入氣象條件復雜的空間，以及防止誤入禁飛區等。

2.1 雷達威脅

雷達具有遠距離探測、識別和跟蹤目標的功能，雷達威脅是航跡規劃中一個絕對不能忽視的因素。針對雷達散射截面固定的無人機，雷達信噪比公式［16］可簡化為

4 基于多精度規劃窗口的航跡規劃算法

對于給定規劃窗口和規劃精度的航跡規劃問題，本文采用人工ACO算法進行優化。ACO算法是通過模擬真實蟻群的覓食行為而來的一種仿生算法，所以既保留著真實螞蟻的特征又具備一些真實螞蟻沒有的特征。

4.1 基于ACO算法的單精度航跡優化

基本ACO算法的偽代碼如算法1所示。

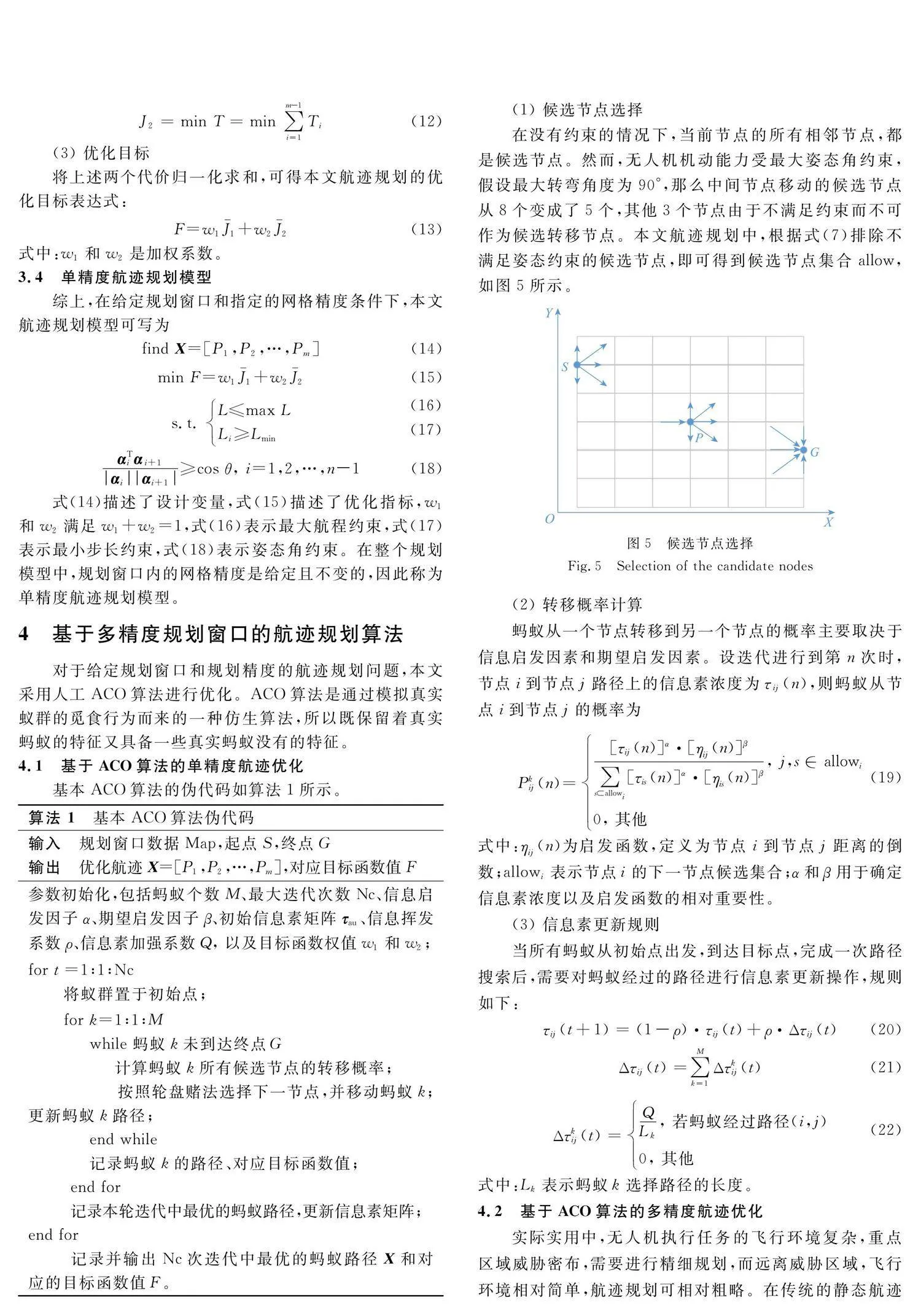
（1） 候選節點選擇

在沒有約束的情況下，當前節點的所有相鄰節點，都是候選節點。然而，無人機機動能力受最大姿態角約束，假設最大轉彎角度為90°，那么中間節點移動的候選節點從8個變成了5個，其他3個節點由于不滿足約束而不可作為候選轉移節點。本文航跡規劃中，根據式（7）排除不滿足姿態約束的候選節點，即可得到候選節點集合allow，如圖5所示。

（2） 轉移概率計算

螞蟻從一個節點轉移到另一個節點的概率主要取決于信息啟發因素和期望啟發因素。設迭代進行到第n次時，節點i到節點j路徑上的信息素濃度為τij（n），則螞蟻從節點i到節點j的概率為

Pkij（n）=［τij（n）］α·［ηij（n）］β∑sallowi［τis（n）］α·［ηis（n）］β， j，s∈allowi

0， 其他（19）

式中：ηij（n）為啟發函數，定義為節點i到節點j距離的倒數;allowi表示節點i的下一節點候選集合;α和β用于確定信息素濃度以及啟發函數的相對重要性。

（3） 信息素更新規則

當所有螞蟻從初始點出發，到達目標點，完成一次路徑搜索后，需要對螞蟻經過的路徑進行信息素更新操作，規則如下：

τij（t+1）=（1－ρ）·τij（t）+ρ·Δτij（t）（20）

Δτij（t）=∑Mk=1Δτkij（t）（21）

Δτkij（t）=QLk， 若螞蟻經過路徑（i，j）

0， 其他（22）

式中：Lk表示螞蟻k選擇路徑的長度。

4.2 基于ACO算法的多精度航跡優化

實際實用中，無人機執行任務的飛行環境復雜，重點區域威脅密布，需要進行精細規劃，而遠離威脅區域，飛行環境相對簡單，航跡規劃可相對粗略。在傳統的靜態航跡規劃研究中，大都不會細化飛行環境復雜程度，一般在整個規劃窗口內，采用同一精度進行規劃，而后再在動態航跡規劃階段根據需求進行航跡調整。如果靜態規劃階段，規劃精度高，則會造成計算耗時長、優化慢、占用存儲空間等情況，如果靜態規劃階段精度較低，雖然克服了計算耗時和存儲占用的問題，但航跡粗略，不利于后期的動態快速調整。

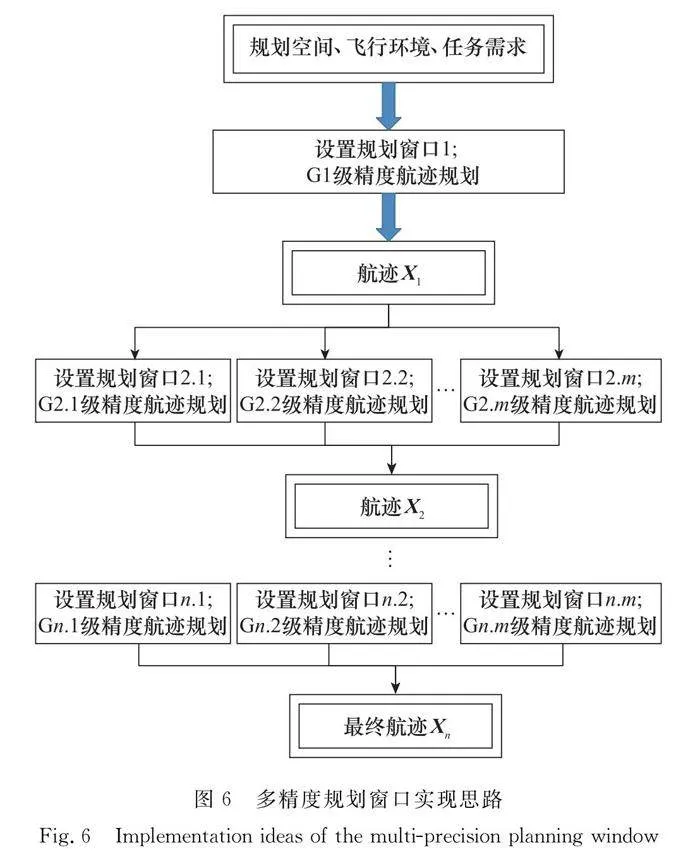
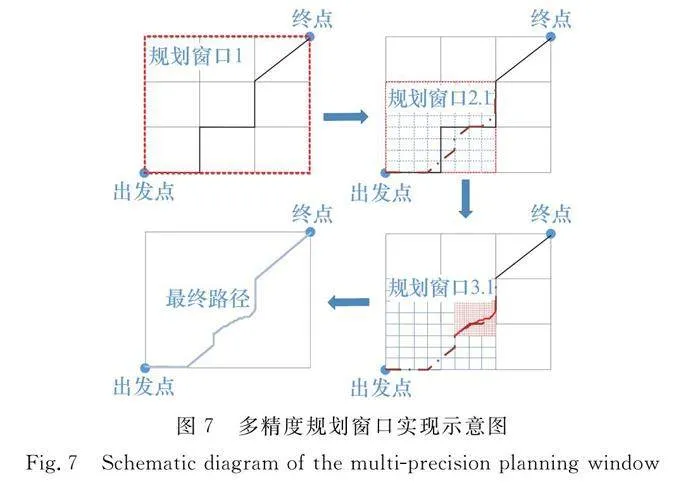
為了提高規劃效率，節約計算資源，本文提出一種多精度規劃窗口策略，即根據飛行環境復雜性與任務需求特點，對不同局部區域采用不同的規劃精度和參數配置，以期達到整體相對最優、局部精細的高效規劃效果。思路大致如圖6所示。

由上述策略可知，在多精度窗口的規劃規則中，首先需要根據無人機的起始與終點位置，對航跡進行一次粗精度優化，得到粗略航跡，確定無人機大致飛行線路;而后以該粗略航跡為基準，按照一定原則劃分多個局部規劃窗口，窗口中無人機的起止位置以輸入的參考航跡在窗口中的起止位置為準，相鄰窗口的起止位置或航跡互不重疊，且不同窗口的規劃精度可略有不同;局部窗口設定后，對每一個局部窗口，設置網格精度，而后并行地對每一個局部規劃窗口進行細粒度的航跡規劃;最終的優化航跡，是所有窗口更新后的航跡集合，是一條多精度融合的優化航跡。

圖7給出了一次多精度規劃示例，為了便于表達，每次僅選取一個局部規劃窗口。

of the multi-precision planning window

基于多精度規劃窗口的無人機航跡規劃算法偽代碼如算法2所示。

算法2中，在第i（igt;1）次優化循環中，根據現有飛行航跡Xi-1和初始規劃窗口Map1，由用戶根據偏好自定義劃分局部規劃窗口范圍。劃分出若干個局部規劃窗口后，自動設置每個局部規劃窗口的規劃精度（即網格大小）為局部窗口大小的1/n，其中n由用戶根據偏好給出。例如：對于一個12 km×10 km的規劃窗口，設置n=10，那么當前規劃窗口的規劃精度即為1.2 km×1 km。

局部規劃窗口確定后，算法根據局部規劃窗口中威脅/障礙分布情況，設置每個窗口下優化模型的權值因子w1和w2。首先，算法自動計算局部規劃窗口中，威脅概率大于0的網格點在整個規劃空間的占比，當占比大于某個閾值時，認為是威脅密集分布;小于某個閾值時，認為是威脅稀疏分布。具體閾值由用戶在算法中給定。如果局部窗口中的威脅稀疏分布，令w1gt;w2;反之，則w1lt;w2，具體數值由用戶根據偏好給出。

隨后的航跡優化中，以飛行航跡Xi-1與局部窗口的交點作為局部規劃窗口中無人機飛行的起點/終點。若規劃窗口相交，則取相交區間內航跡的中點為相鄰窗口航跡的起點或終點。

局部規劃窗口中的每一次迭代規劃，均采用基本ACO算法，但每個窗口的優化模型參數，會根據局部窗口的不同而有所調整，如規劃精度、目標函數值的權值，都會各有不同。

每一輪局部窗口規劃完成后，將飛行航跡Xi-1中的對應部分替換為局部飛行航跡sub Xi，得到最終的第i（igt;1）輪優化后的無人機飛行航跡Xi。

5 仿真分析

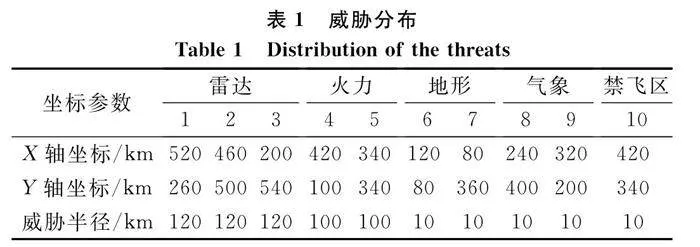
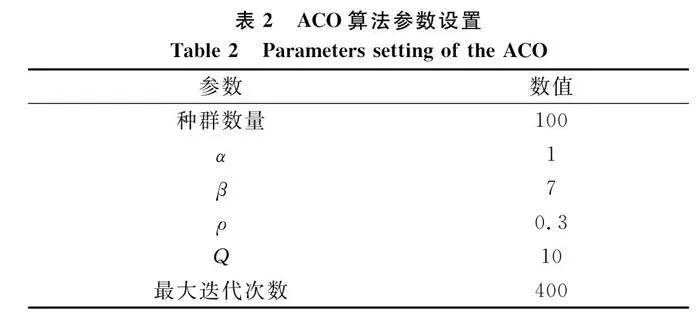
假設無人機飛行區域為600×600 km2，無人機最小步長為2 km，威脅分布如表1所示，威脅點坐標和威脅半徑隨機給出。在規劃開始前，首先需要對無人機飛行空間區域進行網格劃分，網格的交點即為航跡節點，然后根據威脅位置與威脅作用半徑在空間網格區域表示出來。本文所用ACO算法的相關參數設置如表2所示。

5.1 飛行環境對航跡規劃影響分析

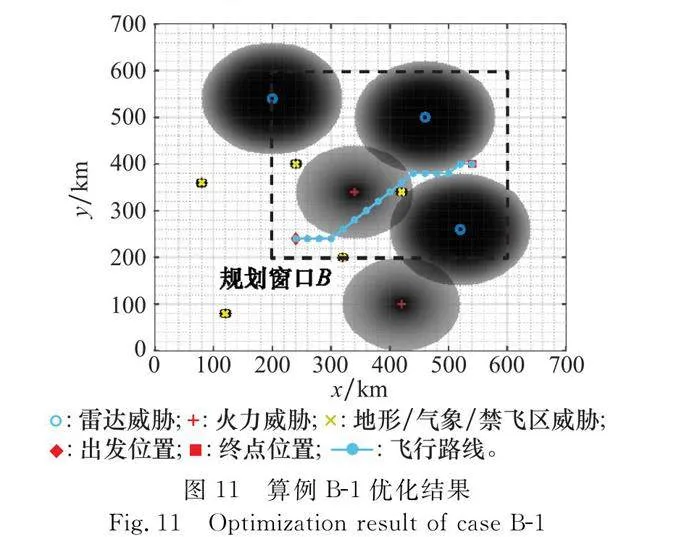
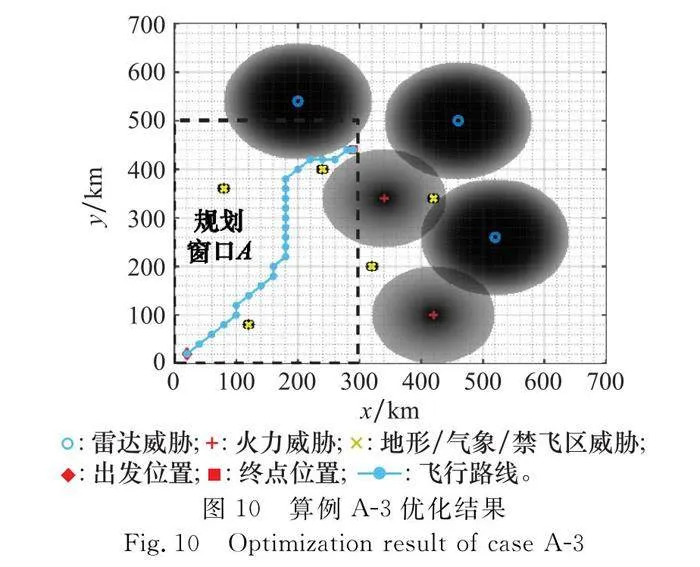
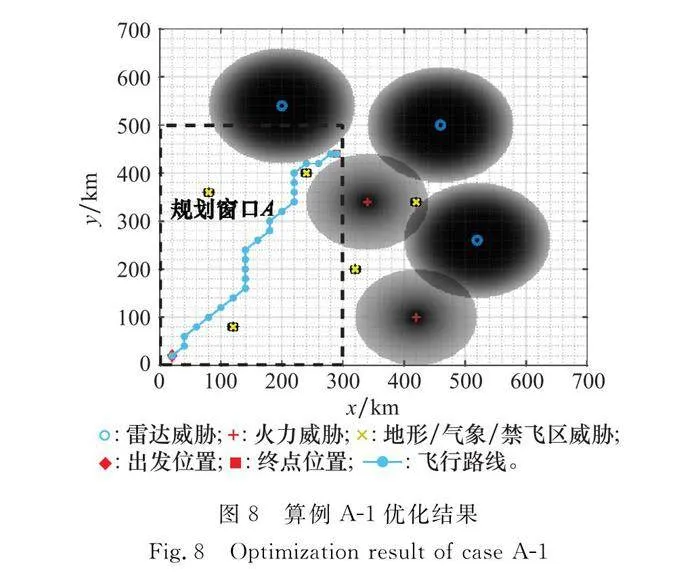
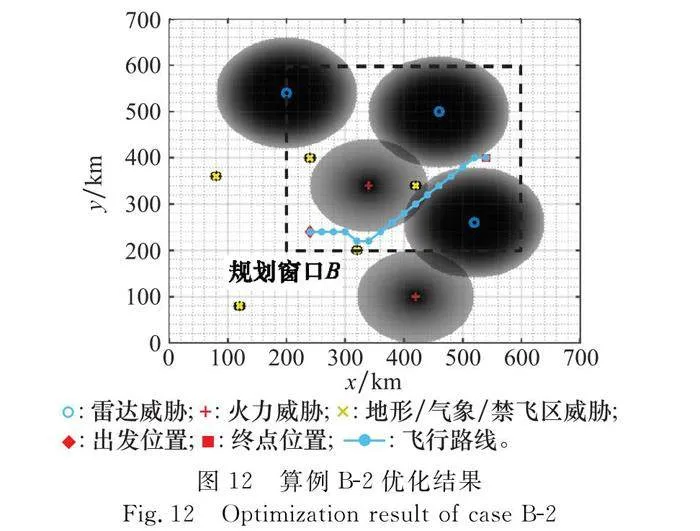
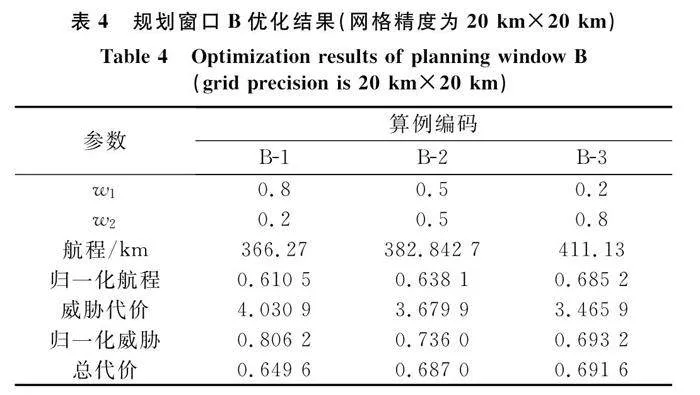
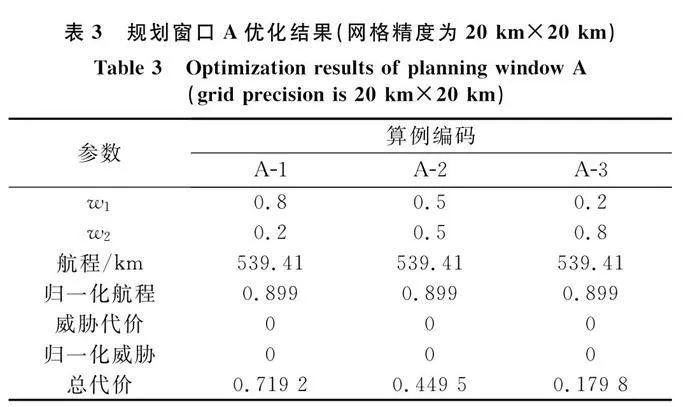
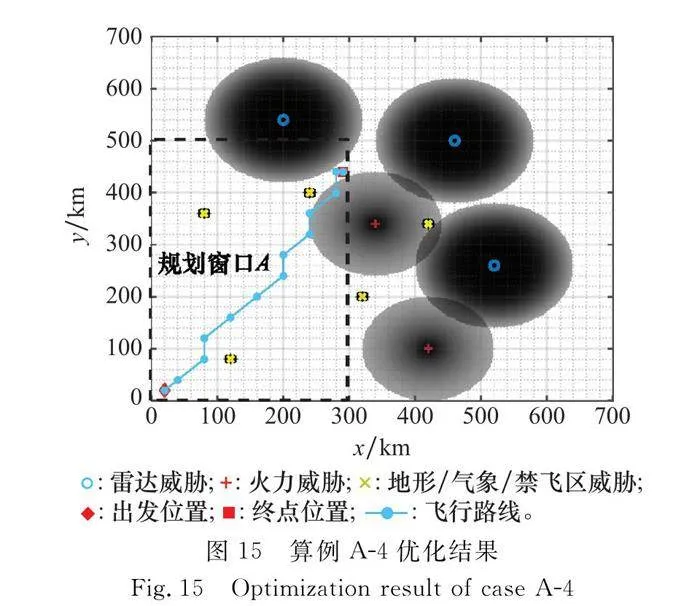
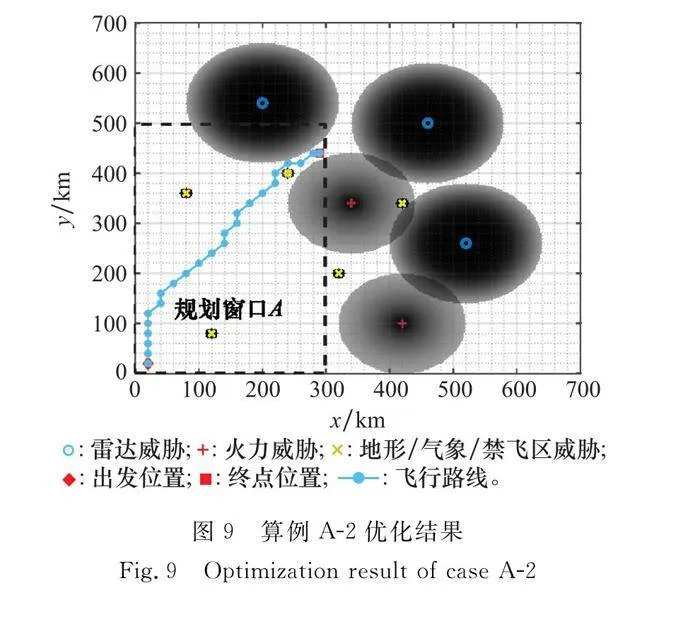
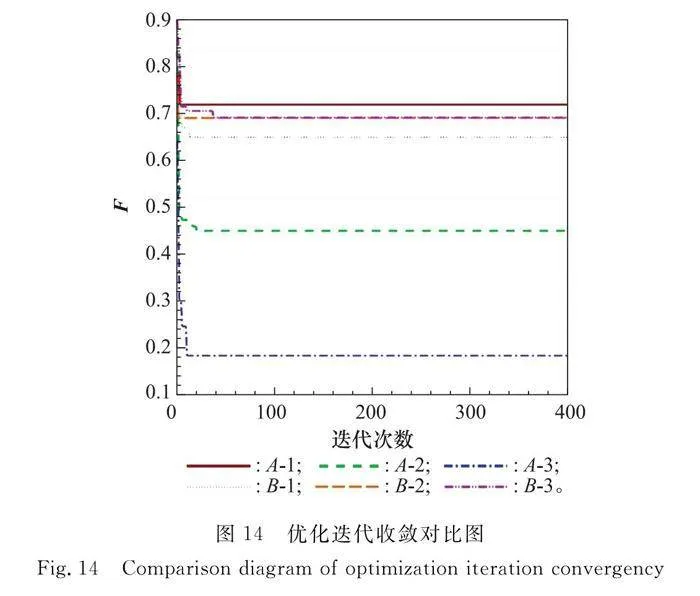
為分析飛行環境對航跡規劃的影響，本節中設計兩個規劃窗口，規劃窗口A的邊界范圍為［0，0］至［300，500］，無人機起飛位置為［20，20］，目標位置為［290，440］;規劃窗口B的邊界范圍為［200，200］至［600，600］，無人機起飛位置為［240，240］，目標位置為［540，400］。通過戰場環境仿真可以知曉，規劃窗口A中，各威脅稀疏分布，而規劃窗口B中，威脅密集分布。ACO算法參數采用表2的設置。改變目標函數值中的權重因子，航跡規劃結果對比如表3和表4所示，算例的最終飛行航跡如圖8～圖13所示。圖中，菱形表述出發點，方形表示目標點，兩者之間的實線為飛行航跡，威脅分布中，各個網格灰度的深淺，表征了其威脅概率的大小，顏色越深，威脅概率越大。圖14給出了本節中各個算例的迭代收斂情況。

從仿真結果可知：

（1） 當威脅稀疏分布時（見表3、圖8～圖10），總能找到一條威脅代價為0的最短飛行航跡為最優航跡，最優航跡與權重分配關系不大。但是權重會影響收斂速度，威脅的權重越小，越利于收斂（見圖14）。

（2） 當威脅密集分布（見表4、圖11～圖13），無人機航跡不可避免需要經過威脅區域時，權重分配會對優化結果產生影響。當航程權重大時，趨向于搜索一條航程短，但是威脅相對較大的路徑;當航程權重小時，趨向于搜索一條航程相對較長，但威脅相對較小的路徑。如表4所示，隨著航程權重的下降、威脅代價權重的增加，得到的最優路徑呈現航程增大而威脅代價降低的趨勢。

（3） 本文算法中，當迭代次數為400時，一次航跡規劃時間大概是30 s，從圖14中可知，60代左右即可收斂到較好的航跡。從側面證明了本文采用的航跡規劃算法的快速收斂性。

（4） 綜上可知，針對不同的飛行環境，需要根據任務需求設置適當的權重系數。而在真實戰場環境中，威脅的稀疏分布與密集分布并存，如果針對不同的局部環境采取不同的規劃窗口進行和優化參數設置，將更利于航跡尋優。

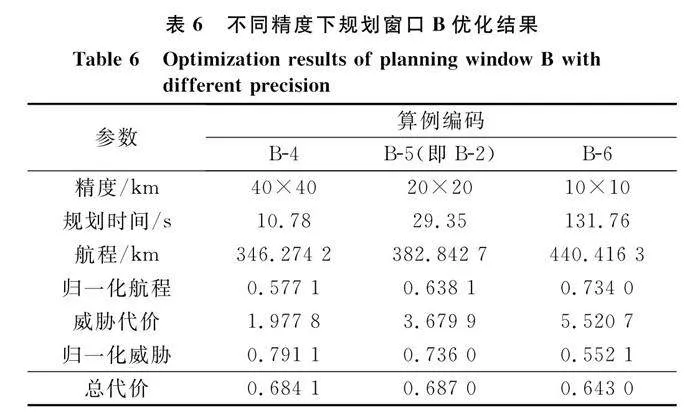
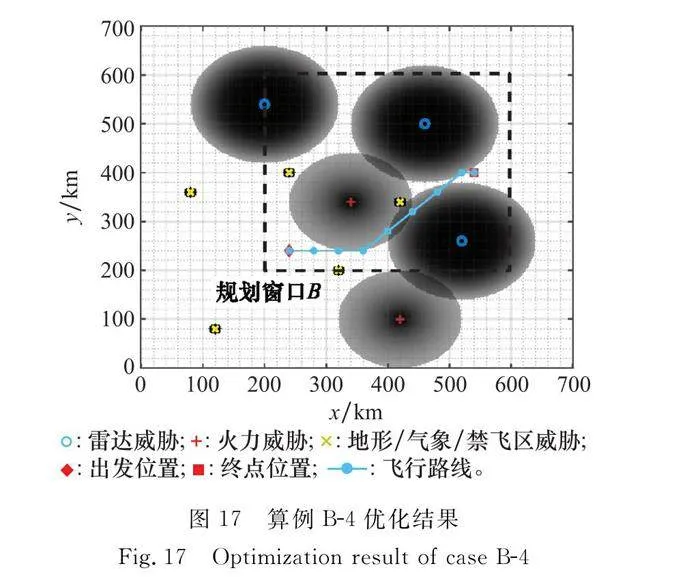
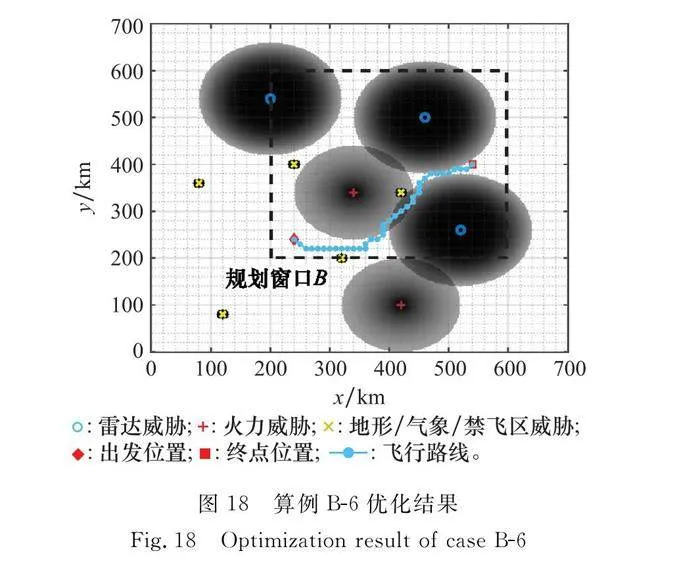
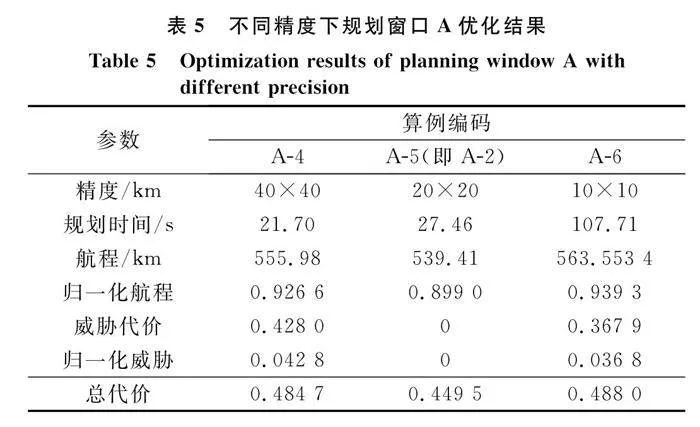
5.2 規劃窗口精度對航跡規劃影響分析

本節采用與第5.1節相同的戰場環境配置、算法參數配置以及規劃窗口配置。為了分析規劃窗口精度對航跡優化結果的影響，各個仿真算例中，目標函數權值w1和w2均固定為0.5，僅改變網格精度。規劃結果如表5和表6所示，對應算例的航跡優化結果如圖15～圖18所示。需要指出的是，在本文優化模型中，威脅代價與網格精度息息相關，本文定義的威脅代價是飛行航跡中各個網格節點威脅概率的和，隨著網格精度的增加，飛行航跡上包含的網格節點必然增多，則威脅概率的和必然增長。因此，本文所定義的威脅代價只適合在同等網格精度下進行對比，在不同網格精度下，威脅代價不具備可比性。

從上述仿真結果中可以看出：

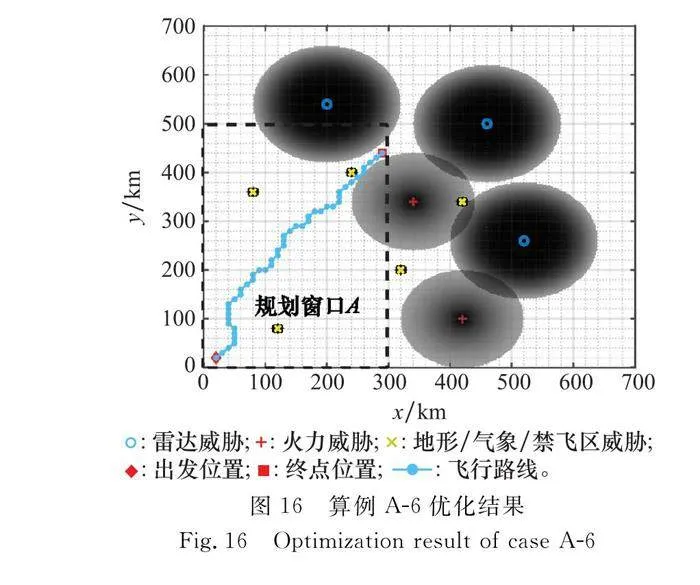
（1） 精度越高，規劃時間越長，航跡越精細，所需算法迭代次數越多。如圖16所示，在相同迭代次數內，其優化的航跡并不優于算例A-2。這是因為隨著規劃精度的提升，搜索空間倍數增長，高精度搜索需要更多的迭代嘗試，如果限制迭代次數，很難搜到最優航跡。

（2） 規劃精度的不恰當設置，會影響算法尋優。當窗口精度較低時，由于網格粒度大，在威脅相對密集區域，很難找到零威脅的路徑。如圖15所示，本存在威脅為零且航程更短的飛行航跡（算例A-2），但由于規劃精度的不恰當限制，算法無法搜索到這樣一條航跡，只能退而求其次。

（3） 對比表5和表6可知，威脅稀疏區域適合低精度搜索，威脅相對密集區域，需要提高規劃精度和算法迭代次數。

5.3 多精度規劃窗口下的航跡優化

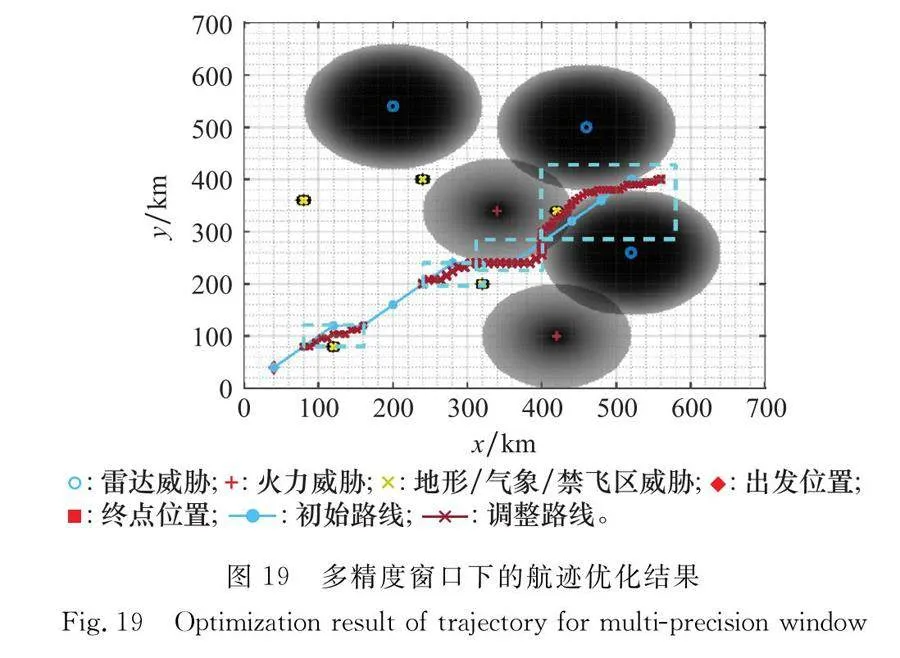
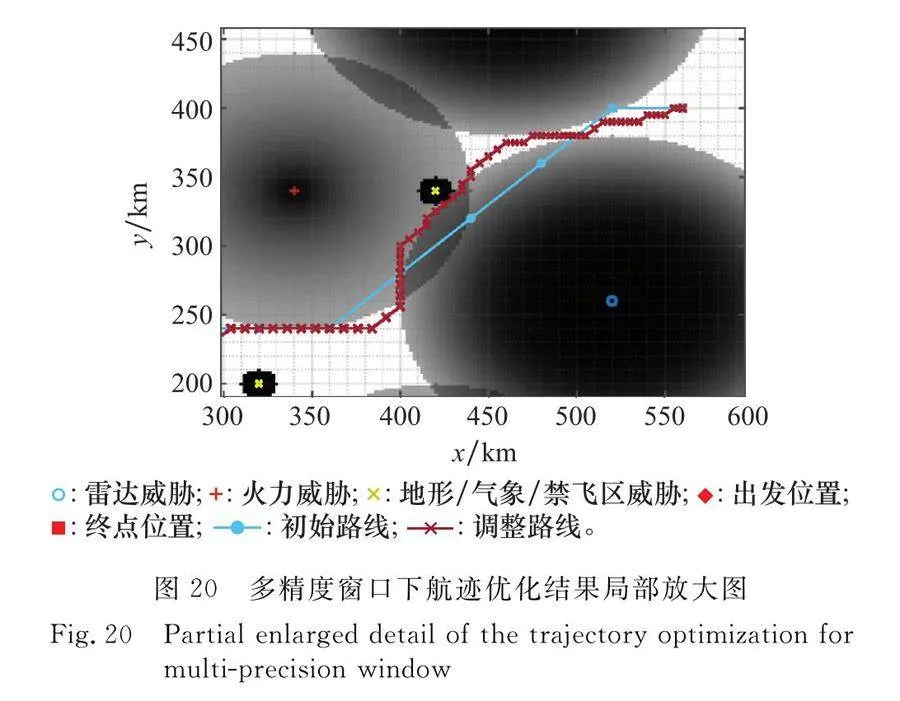
采用同樣的戰場環境配置、算法參數配置以及規劃窗口配置，本節主要將提出的多精度規劃窗口方法應用于仿真算例。在本節中，無人機的出發點為［40，40］km，目標點為［560，400］km。在第一輪優化中，網格精度設置為40 km×40 km，優化結果即初始飛行路線如圖19中實心圓連成的航跡所示，總航程為669.12 km。第二輪中，本文的算法由戶偏好生成4個局部規劃窗口，每個局部規劃窗口的規劃精度為其規劃范圍的1/10，每個窗口的目標函數權值，由算法自動識別威脅分布后給出，即各個窗口中的規劃精度和權值參數設置各不相同。規劃完成后，總的航程為703.68 km。從圖19和圖20可知，第二輪航跡調整后，航程的增加主要來自于威脅密集分布區域，在該區域，通過多精度窗口并行優化，算法給威脅代價賦予了較大的權值，則優化結果偏向于以犧牲航程為代價，規避威脅較高區域。在威脅稀疏區域，由于總是能找到威脅為0的航跡，因此這部分區域的航跡規劃，總是以航程最小為優化目標。

圖19和圖20的優化過程中，最高的航跡精度約為5 km，總的優化耗時約為132 s。以5 km×5 km的網格精度為規劃精度，采用表1和表2的參數設置，進行一次沒有多精度規劃窗口的航跡規劃，程序運行約15 min后，仍舊未輸出優化結果。這是因為初始規劃窗口范圍較大，在初始規劃窗口范圍內采用較高的規劃精度，極大地增加了網格節點數量，從而使得算法的搜索空間巨大，ACO算法的尋優收斂速度變慢，很難在短時間內獲取搜索結果。從此項對比中可知，在同等規劃精度需求下，本文提出的方法，相比傳統方法而言，可以較好地提高收斂速度，更快速地獲取優化結果。

基于多精度規劃窗口的航跡優化表明，本文提出的方法，可以有效改善和調整飛行環境布局復雜條件下的無人機飛行航跡，其并行優化能力，可保證航跡規劃效率。

6 結 論

航跡規劃的優劣，決定了無人機能否在復雜多變的環境下順利完成任務，并使得任務代價最優。本文基于現有蟻群航跡規劃算法，在其并行能力基礎上提出一種多精度規劃窗口方法，可針對局部飛行環境特點，自動配置局部規劃窗口、規劃精度和規劃參數，并行地開展多精度窗口航跡調整，可在較短時間內優化出一條適應戰場環境的飛行航跡。仿真分析表明，為了得到滿足需求的最優航跡，航跡優化算法需要根據不同的飛行環境和不同的規劃精度，適配不同的優化參數。威脅稀疏分布區域，適合精度低、威脅權重小的優化，威脅密集區域，適合精度高、航程權重小的優化。如果針對不同的局部環境采取不同的規劃窗口進行規劃和優化參數設置，將更利于航跡尋優。本文提出的方法可以在初始航跡基礎上，進一步有效改善和調整飛行環境復雜條件下的無人機飛行航跡，并且其具備并行優化能力，可保證航跡規劃效率。需要指出的是，本文提出的多精度窗口方法，不局限于ACO算法，也可適用于其他具備并行能力的優化算法。

本文當前只考慮了二維平面的航跡規劃問題，在實際應用中，三維場景更為普遍。在進一步的研究中，將考慮將相關研究成果拓展至三維的情形，以提高研究成果的實用價值。

參考文獻

［1］ 霍霄華. 多UCAV動態協同任務規劃建模與滾動優化方法研究［D］. 長沙： 國防科技大學， 2007.

HUO X H. Research on modeling and rolling optimization methods for multi-UCAV dynamic cooperative mission planning［D］. Changsha： National University of Defense Technology， 2007.

［2］ 路晶， 史宇， 張書暢， 等. 無人機航跡規劃算法綜述［J］. 航空計算技術， 2022， 52（4）： 131-134.

LU J， SHI Y， ZHANG S C， et al. A review of UAV trajectory planning algorithms［J］. Aeronautical Computing Technique， 2022， 52（4）： 131-134.

［3］ 沈林成， 陳璟， 王楠. 飛行器任務規劃技術綜述［J］. 航空學報， 2014， 35（3）： 593-606.

SHEN L C， CHEN J， WANG N. Overview of air vehicle mission planning techniques［J］. Acta Aeronautica et Astronautica Sinica， 2014， 35（3）： 539-606.

［4］ 陳守鳳. 基于改進人工勢場法的多無人機協同航跡規劃算法研究［D］. 哈爾濱： 哈爾濱工業大學， 2017.

CHEN S F. An improved artificial potential field based path planning algorithm for cooperative collision of multiple unmanned aerial vehicles［D］. Harbin： Harbin Institute of Technology， 2017.

［5］ 張帥， 李學仁， 張鵬， 等. 基于改進A*算法的無人機航跡規劃［J］. 飛行力學， 2016， 34（3）： 39-43.

ZHANG S， LI X R， ZHANG P， et al. UAV path planning based on improved A* algorithm［J］. Flight Dynamics， 2016， 34（3）： 39-43.

［6］ VINCENT R， MOHAMMED T， GILLES L. Comparison of parallel genetic algorithm and particle swarm optimization for realtime UAV path planning［J］. IEEE Trans.on Industrial Informatics， 2013， 9（1）： 132-141.

［7］ 范林玉. 航跡規劃遺傳模擬退火算法研究［D］. 重慶： 重慶大學， 2010.

FANG L Y. Flight path plan research based on genetic and simulated annealing algorithm［D］. Chongqing： Chongqing University， 2010.

［8］ 陸天和， 劉莉， 賀云濤， 等. 多無人機航跡規劃算法及關鍵技術［J］. 戰術導彈技術， 2020（1）： 85-90.

LU T H， LIU L， HE Y T， et al. Multi-UAV path planning algorithm and key technology［J］. Tactical Missile Technology， 2020（1）： 85-90.

［9］ HOANG V T， PHUNG M D， DINH T H， et al. Angle-encoded swarm optimization for UAV formation path planning［C］∥Proc.of the IEEE International Conference on Intelligent Robots and Systems， 2018： 5239-5244.

［10］ SHAO Z， YAN F， ZHOU Z， et al. Path planning for multi-UAV formation rendezvous based on distributed cooperative particle swarm optimization［J］. Applied Sciences， 2019， 9： 2621.

［11］ GAMBARDELLA L M， DORIGO M. ANT-Q： a reinforcement learning approach to the traveling salesman problem［C］∥Proc.of the 12th International Conference on Machine Learning， 1995： 252-260.

［12］ 段海濱， 王道波. 蟻群算法的全局收斂性研究及改進［J］. 系統工程與電子技術， 2004， 26（10）： 1506-1509.

DUAN H B， WANG D B. Research and improvement on the global convergence of ant colony algorithm［J］. Systems Engineering and Electronics， 2004， 26（10）： 1506-1509.

［13］ 肖紹. 基于改進蟻群算法的無人機航跡規劃研究［D］. 南昌： 南昌航空大學， 2016.

XIAO S. The research for route planning of UAV based on improved ant colony algorithm［D］. Nanchang： Nanchang Hangkong University， 2016.

［14］ 陳冬. 基于粒子群優化算法的無人機航跡規劃［D］. 西安： 西北工業大學， 2007.

CHEN D. UAV path planning based on particle swarm optimization［D］." Xi’an： Northwest Polytechnical University， 2007.

［15］ 張延松. 基于遺傳算法的無人機航跡規劃研究［D］. 長沙： 中南大學， 2010.

ZHANG Y S. UAV path planning based on the genetic algorithm［D］. Changsha： Central South University， 2010.

［16］ 胡中華. 基于智能優化算法的無人機航跡規劃若干關鍵技術研究［D］. 南京： 南京航空航天大學， 2011.

HU Z H. Research on some key techniques of UAV path planning based on intelligent optimization algorithm［D］. Nanjing： Nanjing University of Aeronautics and Astronautics， 2021.

［17］ 陳俠， 毛海亮， 劉奎武. 基于改進自適應蟻群算法的無人機航跡規劃研究［J］. 電光與控制， 2022， 29（9）： 6-10.

CHEN X， MAO H L， LIU K W. Path planning of UAV based on improved adaptive ant colony algorithm［J］. Electronics Optics amp; Control， 2022， 29（9）： 6-10.

［18］ 鄭弈， 謝亞琴. 基于Dijkstra算法改進的飛行器航跡快速規劃算法［J］. 電子測量技術， 2022， 45（12）： 73-79.

ZHENG Y， XIE Y Q. Improved fast aircraft path planning algorithm based on Dijkstra algorithm［J］. Electronic Measurement Technology， 2022， 45（12）： 73-79.

［19］ 李昱， 李紅燁. 針對特殊威脅的改進人工勢場法航跡規劃［J］. 探測與控制學報， 2022， 44（4）： 111-117.

LI Y， LI H Y. An improbed APF route planning method for special threats［J］. Journal of Dectection amp; Control， 2022， 44（4）： 111-117.

［20］ 韓堯， 李少華. 基于改進人工勢場法的無人機航跡規劃［J］. 系統工程與電子技術， 2021， 43（11）： 3305-3311.

HAN Y， LI S H. UAV path planning based on improved artificial potential field［J］. Systems Engineering and Electronics， 2021， 43（11）： 3305-3311.

［21］ 蔡星娟， 胡釗鳴， 張志霞， 等. 基于高維多目標優化的多無人機協同航跡規劃［J］. 中國科學： 信息科學， 2021， 51（6）： 985-996.

CAI X J， HU Z M， ZHANG Z X， et al. Multi-UAV coordinated path planning based on many-objective optimization［J］. SCIENTIA SINICA Information， 2021， 51（6）： 985-996.

［22］ 余婧， 雍恩米， 陳漢洋， 等. 面向多無人機協同對地攻擊的雙層任務規劃方法［J］. 系統工程與電子技術， 2022， 44（9）： 2849-2857.

YU J， YONG E M， CHEN H Y， et al. Bi-level mission planning method for multi-cooperative UAV air-to-ground attack［J］. Systems Engineering and Electronics， 2022， 44（9）： 2849-2857.

作者簡介

余 婧（1986—），女，副研究員，博士，主要研究方向為飛行器設計、飛行器任務規劃。

吳曉軍（1976—），男，研究員，博士，主要研究方向為飛行器設計。

蔣安林（1986—），男，副研究員，碩士，主要研究方向為飛行器設計與數據分析。

雍恩米（1979—），女，副研究員，博士，主要研究方向為多機協同任務規劃、導彈攻防任務規劃。