同步提取變換去噪的雷達信號調制識別方法

摘 要：針對已有Cohen類時頻分布等方法時頻聚焦能力不足、在低信噪比（signal to noise ratio， SNR）情況下調制識別準確率低的問題，提出一種基于同步提取變換（synchro-extracting transform， SET）去噪的分組卷積神經網絡調制識別方法。所提方法使用SET對雷達信號進行時頻分析，以獲得良好的時頻聚焦性，提高時頻分析的計算效率;通過Viterbi算法搜索估計時頻系數矩陣中的瞬時頻率軌跡，綜合考慮信號能量強度分布與瞬時頻率軌跡的平滑性，并對得到的瞬時頻率軌跡進行中值濾波以去除脈沖噪聲;保留瞬時頻率軌跡鄰域的時頻系數，以達到時頻圖去噪的目的。最后，將去噪后的時頻圖送入具有殘差連接的分組卷積神經網絡進行特征提取與調制識別。實驗結果表明，當SNR為-12 dB時，去噪后的SET時頻圖時頻聚焦性好，調制識別準確率比未去噪的識別準確率提高了13.69%，證明所提出的雷達信號調制識別方法在低SNR條件下對多種復雜調制類型的信號具有良好的識別性能。

關鍵詞： 雷達信號調制識別; 同步提取變換; 瞬時頻率估計; 去噪

中圖分類號： TN 957.51 文獻標志碼： A""" DOI：10.12305/j.issn.1001-506X.2024.10.11

Radar signal modulation recognition method based on synchro-extracting

transform denoising

DENG Zhian^1， WANG Zhiguo^1， WANG Sheng’ao^3， SI Weijian^1，2

（1. College of Information and Communication Engineering， Harbin Engineering University， Harbin 15000 China;

2. Key Laboratory of Advanced Marine Communication and Information Technology， Ministry of Industry and

Information Technology， Harbin 15000 China; 3. Department of Science and Information Technology，

Sichuan Jiuzhou Investment Holding Group Company Limited， Mianyang 621000， China）

Abstract： Due to the insufficient time-frequency focusing ability of the existing Cohen-class time-frequency distribution and low modulation recognition accuracy under low signal to noise ratio （SNR）， a grouped convolutional neural network modulation recognition method based on synchronous extracting transform （SET） denoising is proposed. Firstly， SET is used for time-frequency analysis of the radar signals， providing better time-frequency focusing and computational efficiency of time-frequency analysis. Then， the Viterbi algorithm is utilized to search and estimate the instaneous frequency trajectory in the time-frequency coefficient matrix， taking into account the distribution of signal energy intensity and the smoothness of the instaneous frequency trajectory. At the same time， a median filter is applied to remove pulse noise from the obtained instaneous frequency trajectory， and the time-frequency coefficients in the vicinity of the instaneous frequency trajectory are retained to achieve time-frequency image denoising. Finally， the denoised time-frequency images are sent to a grouped convolution neural network with residual connections for feature extraction and modulation recognition. The experimental results demonstrate that， when the SNR is -12 dB， the denoised SET time-frequency images have good time-frequency focusing， and the modulation recognition accuracy is improved by 13.69% compared to the recognition accuracy without denoising. The proposed radar signal modulation recognition method exhibits excellent recognition performance for various complex modulation types of signals under low SNR conditions.

Keywords： radar signal modulation recognition; synchro-extracting transform; instaneous frequency estimation; denoising

0 引 言

雷達信號的調制識別是電子情報偵察、電子支援、威脅警告等系統中的關鍵技術，在雷達電子戰中起著重要作用^［12］。其中，傳統雷達信號的調制識別主要基于雷達信號脈間特征的參數匹配^［34］，適用于脈沖密度較低的常規雷達調制。脈沖雷達壓縮技術的應用有效提高了雷達分辨力，但降低了回波信號的信噪比（signal to noise ratio， SNR），導致調制識別精度降低^［5］。為進一步提高復雜雷達信號的調制識別能力，脈內特征受到廣泛關注。脈內調制識別主要包括基于決策理論的似然假設檢驗法^［69］和基于特征提取的識別方法^［1013］。然而，這些方法計算復雜度高，泛化能力和抗噪聲性能較弱，實用性差，難以滿足復雜雷達脈內調制識別要求^［14］。因此，在低SNR條件下提高復雜雷達信號的調制識別能力在電子戰中具有重要意義。

近年來，利用深度學習實現雷達信號的調制識別成為研究熱點。基于深度學習的雷達信號調制識別主要分為兩類：基于同向正交（in-phase quadrature， IQ）序列的循環神經網絡（recurrent neural network， RNN）調制識別方法^［1517］和基于時頻圖像的卷積神經網絡（convolutional neural network， CNN）調制識別方法。相比于傳統的人工構造特征，前者可以獲得更多、更深層的信號特征，從而提高識別性能，但是網絡復雜度較高。目前主流的方法是將IQ數據從時域轉到時頻域形成二維圖像，將信號序列分類轉變為圖像分類。Li等^［18］利用微調的AlexNet卷積層提取12種雷達信號崔威廉斯分布（Choi-Williams distribution， CWD）圖像的深層特征，當SNR為-6 dB時，識別準確率高達97.58%。Liao等^［19］使用多特征隨機匹配融合網絡學習雷達信號的CWD圖像特征和7個傳統特征。當SNR為-6 dB時，10種雷達信號的平均識別準確率達到了95.4%。Zhang等^［20］使用平滑偽魏格納維利分布（smoothed pseudo Wigner-Ville distribution， SPWVD）和伯恩約旦分布（Born-Jordan distribution， BJD）將信號轉化為兩種時頻圖像，并利用多模態融合模型對兩種圖像特征和8種手工特征進行融合，當SNR為-4 dB時，識別準確率達到了92.5%。針對低截獲概率雷達信號識別率低的問題，郭立民等^［21］提出一種基于CWD和棧式稀疏自編碼器的自動分類識別系統。當SNR為-6 dB時，8種雷達信號的平均識別準確率達到96.4%。邵凱等^［22］提出了一種基于生成對抗網絡和CNN的數字信號調制識別方法，該方法利用SPWVD將調制信號轉化為時頻圖，并利用生成對抗網絡實現對時頻圖的去噪和修復。當SNR為-8 dB時，9種調制信號的平均識別準確率達到了83.3%。

將雷達信號通過Cohen類時頻分布（CWD、SPWVD、BJD）轉換為二維時頻圖，再基于時頻圖進行信號的特征提取與識別已成為一種通用方法。然而，Cohen類時頻分布需要計算三重積分，計算復雜度高，預處理過程實時性較差，且在低SNR下，時頻圖受噪聲影響較大，識別效果較差;同時，已有方法的測試數據集與訓練數據集的信號參數空間一致，這導致測試數據被泄漏到訓練數據中，無法客觀地衡量模型的泛化性能。

本文提出一種基于同步提取變換（synchro-extracting transform， SET）去噪的CNN調制識別方法。通過SET變換結合Viterbi搜索時頻系數矩陣，獲得信號瞬時頻率軌跡，對瞬時頻率軌跡進行中值濾波，并保留其鄰域內的時頻系數，實現時頻圖的去噪。最后，利用分組CNN對去噪后的時頻圖進行特征提取，實現調制信號的識別。SET的時頻聚焦性和計算效率優于已有的Cohen類時頻分布。在進行瞬時頻率軌跡搜索時，Viterbi算法同時考慮了每個時刻下信號能量分布和瞬時頻率軌跡的平滑性，時頻圖去噪后的圖像質量明顯優于去噪前的圖像質量。使用具有殘差結構的分組卷積網絡實現對調制信號的識別，在減少網絡模型參數的同時保證了網絡的識別精度。同時，使用不同的信號參數生成網絡的訓練集與測試集，保證了網絡性能評估的客觀性。

1 基于SET去噪的分組卷積網絡調制識別方法

本文對13種常見雷達信號調制方式進行識別，這些調制方式包括二進制相位調制（binary phase shift keying， BPSK），相位編碼選用巴克碼（Baker code）、連續波（continuous-wave， CW）、二進制頻移鍵控（binary frequency shift keying， 2FSK）、四進制頻移鍵控（quad frequency shift keying， 4FSK）、線性調頻（linear frequency modulation， LFM）、雙LFM（double LFM， DLFM）、正弦調頻（sine frequency modulation， SFM）、偶二次調頻（even quadratic frequency modulation， EQFM）、弗蘭克碼（Frank code）、多相碼（P1 code～P4 code）。

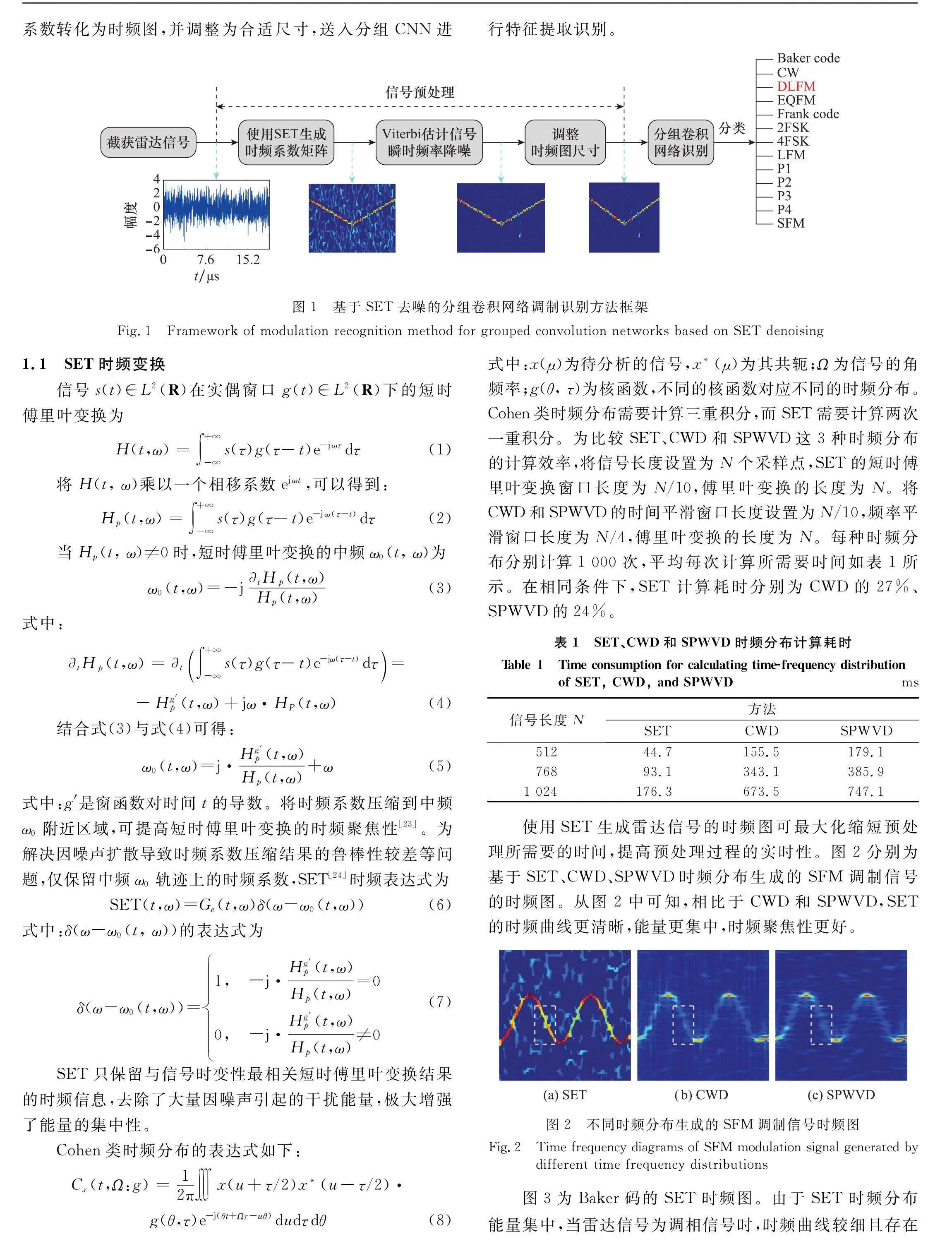
所提出的雷達信號調制識別方法由信號預處理和分類器兩部分組成，如圖1所示。首先，基于SET時頻變換得到截獲信號時頻系數矩陣。然后，利用Viterbi算法搜索時頻系數矩陣以獲得信號的瞬時頻率軌跡并進行中值濾波，保留瞬時頻率鄰域的時頻系數并將其他時頻系數置0，以盡可能去除截獲信號的背景噪聲。最后，將去噪后的時頻系數轉化為時頻圖，并調整為合適尺寸，送入分組CNN進行特征提取識別。

1.1 SET時頻變換

信號s（t）∈L²（R）在實偶窗口g（t）∈L²（R）下的短時傅里葉變換為

H（t，ω）=∫^+∞_－∞s（τ）g（τ－t）e^－jωτdτ（1）

將H（t， ω）乘以一個相移系數e^jωt，可以得到：

H_p（t，ω）=∫^+∞_－∞s（τ）g（τ－t）e^{－jω（τ－t）}dτ（2）

當H_p（t， ω）≠0時，短時傅里葉變換的中頻ω₀（t， ω）為

ω₀（t，ω）=－j_tH_p（t，ω）H_p（t，ω）（3）

式中：

_tH_p（t，ω）=

_t∫^+∞_－∞s（τ）g（τ－t）e^{－jω（τ－t）}dτ=

－H^g′_p（t，ω）+jω·H_P（t，ω）（4）

結合式（3）與式（4）可得：

ω₀（t，ω）=j·H^g′_p（t，ω）H_p（t，ω）+ω（5）

式中：g′是窗函數對時間t的導數。將時頻系數壓縮到中頻ω₀附近區域，可提高短時傅里葉變換的時頻聚焦性^［23］。為解決因噪聲擴散導致時頻系數壓縮結果的魯棒性較差等問題，僅保留中頻ω₀軌跡上的時頻系數，SET^［24］時頻表達式為

SET（t，ω）=G_e（t，ω）δ（ω－ω₀（t，ω））（6）

式中：δ（ω-ω₀（t， ω））的表達式為

δ（ω－ω₀（t，ω））=1，－j·H^g′_p（t，ω）H_p（t，ω）=0

0，－j·H^g′_p（t，ω）H_p（t，ω）≠0（7）

SET只保留與信號時變性最相關短時傅里葉變換結果的時頻信息，去除了大量因噪聲引起的干擾能量，極大增強了能量的集中性。

Cohen類時頻分布的表達式如下：

C_x（t，Ω：g）=

12πx（u+τ/2）x^*（u－τ/2）·

g（θ，τ）e^{－j（θt+Ωτ－uθ）}dudτdθ（8）

式中：x（μ）為待分析的信號，x^*（μ）為其共軛;Ω為信號的角頻率;g（θ， τ）為核函數，不同的核函數對應不同的時頻分布。Cohen類時頻分布需要計算三重積分，而SET需要計算兩次一重積分。為比較SET、CWD和SPWVD這3種時頻分布的計算效率，將信號長度設置為N個采樣點，SET的短時傅里葉變換窗口長度為N/10，傅里葉變換的長度為N。將CWD和SPWVD的時間平滑窗口長度設置為N/10，頻率平滑窗口長度為N/4，傅里葉變換的長度為N。每種時頻分布分別計算1 000次，平均每次計算所需要時間如表1所示。在相同條件下，SET計算耗時分別為CWD的27%、SPWVD的24%。

使用SET生成雷達信號的時頻圖可最大化縮短預處理所需要的時間，提高預處理過程的實時性。圖2分別為基于SET、CWD、SPWVD時頻分布生成的SFM調制信號的時頻圖。從圖2中可知，相比于CWD和SPWVD，SET的時頻曲線更清晰，能量更集中，時頻聚焦性更好。

圖3為Baker碼的SET時頻圖。由于SET時頻分布能量集中，當雷達信號為調相信號時，時頻曲線較細且存在斷裂現象，如圖3（a）所示。圖3（b）為圖3（a）的細節放大圖，放大之后時頻曲線顯示完整。直接使用插值調整原始時頻圖的尺寸，調整后的圖像也會出現時頻曲線斷裂的現象（見圖3（c）），同時調制識別準確率降低。為解決該問題，需先將原始時頻圖保存為高分辯率（每英寸點數）（dots per inch， DPI）圖片，然后再使用插值等方式將圖像尺寸調整為所需大小，在一定程度上保證時頻曲線的完整性，如圖3（d）所示。

1.2 基于Viterbi算法的SET時頻分布去噪

在雷達信號處理中，偵察接收機截獲的信號包含大量噪聲，導致信號時頻特征受到干擾。為消除噪聲影響并保留信號時頻特征，提高調制識別的準確率，提出一種基于Viterbi-SET時頻圖的去噪算法。該算法通過SET變換獲得信號的時頻系數矩陣，利用Viterbi算法搜索時頻系數矩陣中信號真實頻率的瞬時頻率軌跡，并保留每個瞬時頻率鄰域內的時頻系數，最終實現去噪。

為簡單起見，本文只考慮單分量雷達信號。單分量雷達信號r（t）經SET時頻變換生成時頻系數矩陣TFI（t_i， ω_j），其中i=1，2，…，n;j=1，2，…，m。每個時刻t都對應一個瞬時頻率ω，將ω按時間順序連接，獲得信號的瞬時頻率軌跡ω（t）。t₁到t_n之間的所有瞬時頻率軌跡構成集合K，選擇一條合適的軌跡：

Trace=argminω（t）∈K［∑n-1i=ig（ω（t_i），ω（t_i+1））+

∑ni=1f（TFI（t_i，ω（t_i）））］=

argminω（t）∈K p（ω（t）;t₁，t_n）（9）

讓式（9）最小化，實現瞬時頻率估計。

其中，p（ω（t）; t t_n）是懲罰函數g（x， y）和f（x）沿軌跡ω（t）從t₁到t_n的和;g（x， y）考慮頻率估計的平滑性;f（x）考慮瞬時頻率處的能量大小。函數g（x， y）=g（|x-y|）是關于x和y之間絕對距離|x-y|的非遞減函數（其中x=ω（t_i）和y=ω（t_i+1）是相鄰點的瞬時頻率），f（x）是關于x=TFI（t_i， ω（tⁱ））的非遞增函數。在某一時刻下，某個頻率處的時頻系數模值越大，其就越可能是該時刻下的瞬時頻率。對于某時刻t，時頻系數按照非遞增順序排列：

TFI（t，ω₁）≥TFI（t，ω₂）≥…≥TFI（t，ω_m）（10）

則f（x）可以寫成以下形式：

f（TFI（t，ω_j））=j－1（11）

在低SNR環境下，實際瞬時頻率位于第j個點的概率隨著j的增加而下降，即時頻值較大的點是實際瞬時頻率點的概率較大。因此，當g（x， y）為常數時，瞬時頻率估計僅取決于時頻系數最大值的位置，g（x， y）表達式為

g（x，y）=0， |x－y|≤Δ

c（|x－y|－Δ）， |x－y|gt;Δ（12）

式中：c是懲罰系數的權重;Δ是相鄰點之間瞬時頻率變化期望的最大值，相鄰點瞬時頻率變化較小時，懲罰值為0。當Δ→∞時，式（9）變為僅由時頻系數最大值決定。g（x， y）有利于消除算法中的非最優路徑。

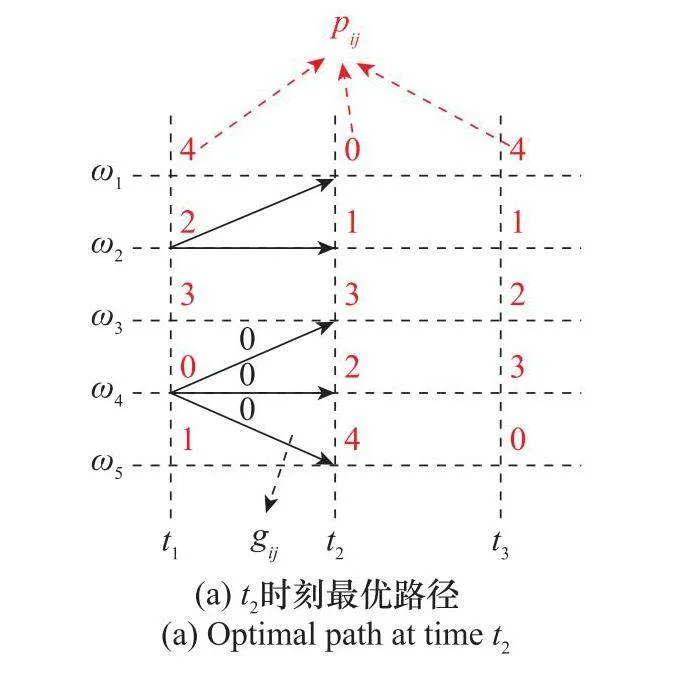
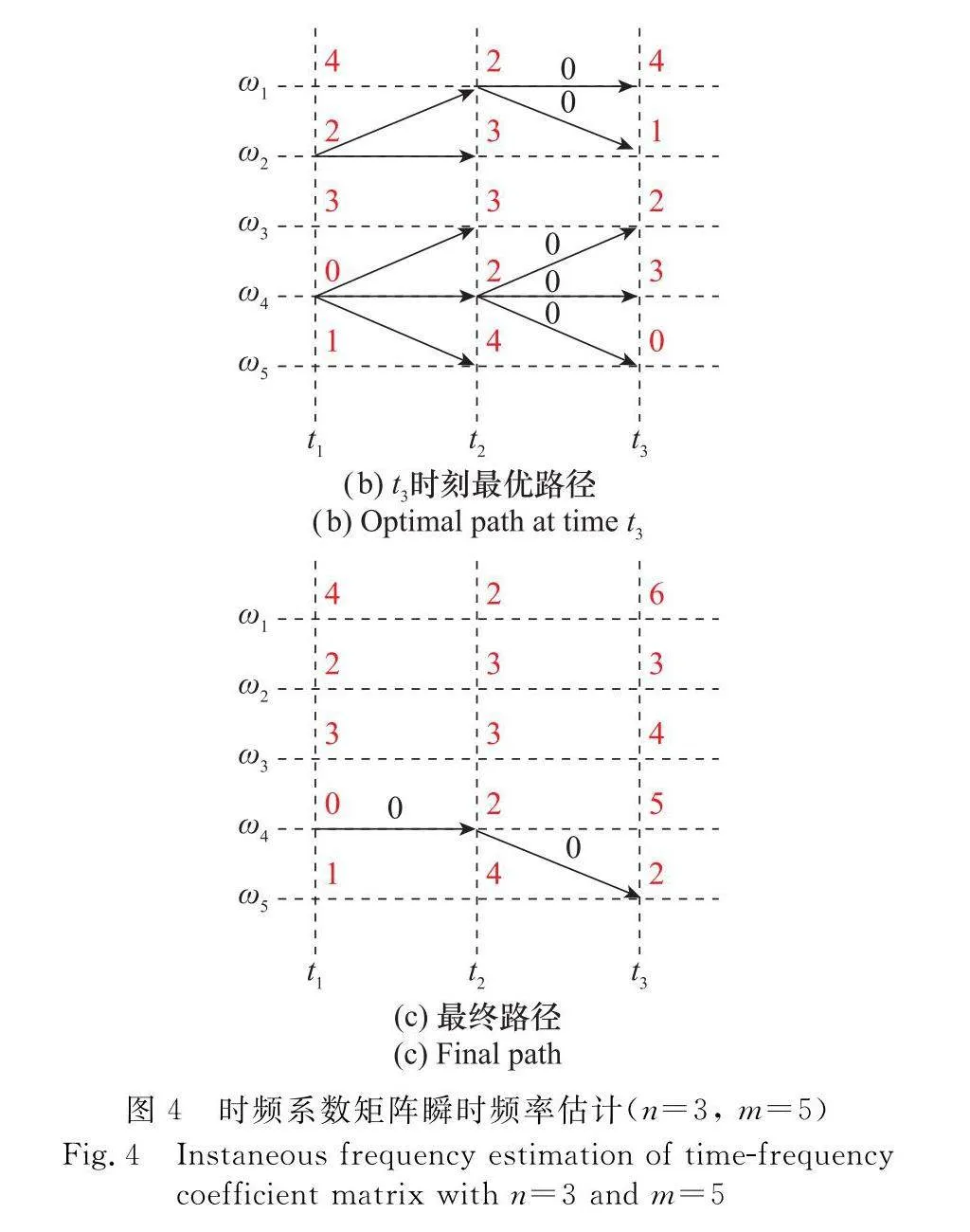
最優路徑的尋找步驟如下：在一個n=3，m=5的時頻系數矩陣中，令f_ij=f（TFI（t_i， ω_j）），g_ij=g（ω_i， ω_j），取c=2.5，Δ=1。在初始狀態下，每個節點的懲罰值p_ij=f_ij，如圖4（a）所示。以（t₂，ω₁）為例，在t₂時刻下，每個節點的最佳路徑懲罰函數為

p_2j=minl=1，2，…，5［p_1l+g_lj］+f_2j（13）

前一時刻的5個節點懲罰值p_1j分別為4、2、3、0、1，到達（t ω₁）的5條路徑的懲罰值g_l1分別為0、0、2.5、5、7.5，這5條路徑的累積懲罰值分別為4、2、5.5、5、8.5，取最小值2，因此只保留（t ω₂）→（t ω₁）這條路徑，此時（t ω₁）的懲罰值更新為0+2=2，如圖4（b）所示。每個節點的最終懲罰值如圖4（c）所示。在t₃時刻的5個節點中，（t₃， ω₅）的最終懲罰值最小，所以由（t₃， ω₅）向前回溯，得到最終的瞬時頻率估計路徑為（t ω₄）→（t ω₄）→（t₃， ω₅）。

基于Viterbi-SET時頻圖去噪算法的實現步驟如下：首先通過SET時頻變換生成雷達信號的時頻系數矩陣，然后使用式（9）定義的懲罰函數向前搜索瞬時頻率路徑，每個時刻下的頻率節點僅保留一條最優路徑并更新節點的懲罰值。在所有時刻搜索完畢后，從懲罰值最小的節點向前回溯，獲得最有可能接近真實頻率的瞬時頻率軌跡。對該瞬時頻率進行21階中值濾波，進一步去除頻率估計中的脈沖噪聲。保留瞬時頻率鄰域10×2區域的時頻系數，并將其他時頻系數置0，以達到去除噪聲的效果。使用去噪后的時頻系數矩陣生成時頻圖，送入CNN，實現對調制信號的識別。

1.3 分組卷積網絡調制識別模型

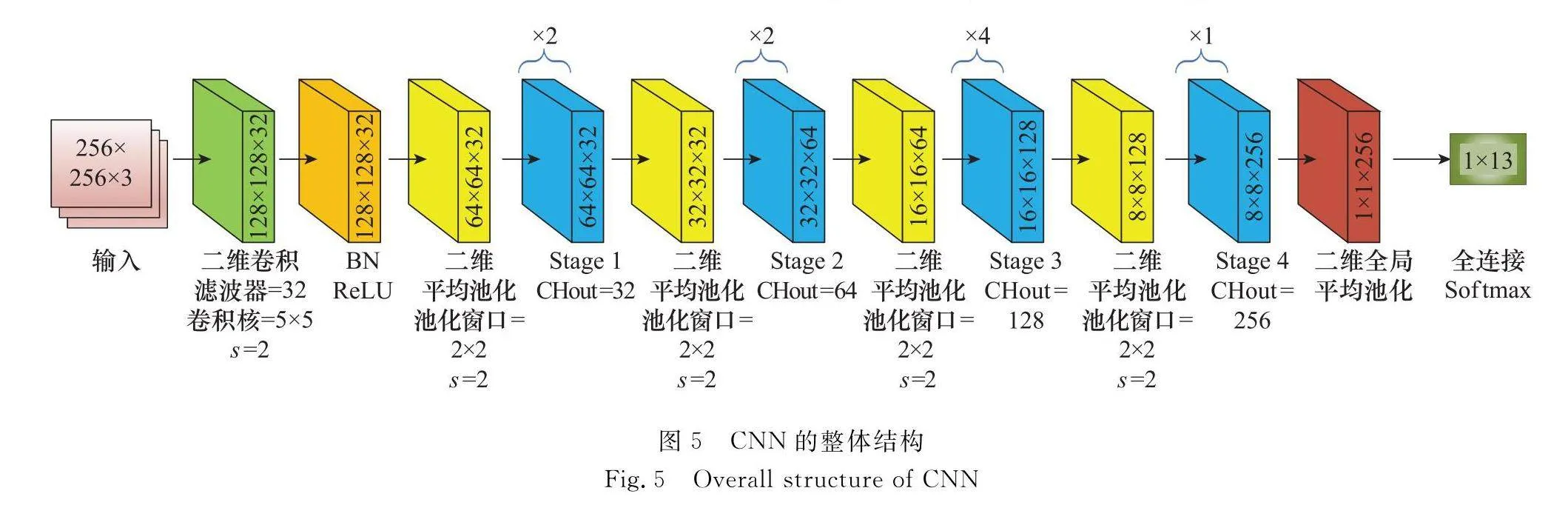
在獲得去噪的時頻圖后，將這些圖像送入CNN進行特征的提取和識別。為了提高網絡的識別性能，利用分組卷積并引入殘差結構，解決了訓練過程中梯度消失、梯度爆炸、訓練網絡不收斂以及因網絡參數量龐大而不適合在邊緣設備部署的問題。CNN的整體結構如圖5所示。圖5中，CHout表示分組卷積塊輸出。

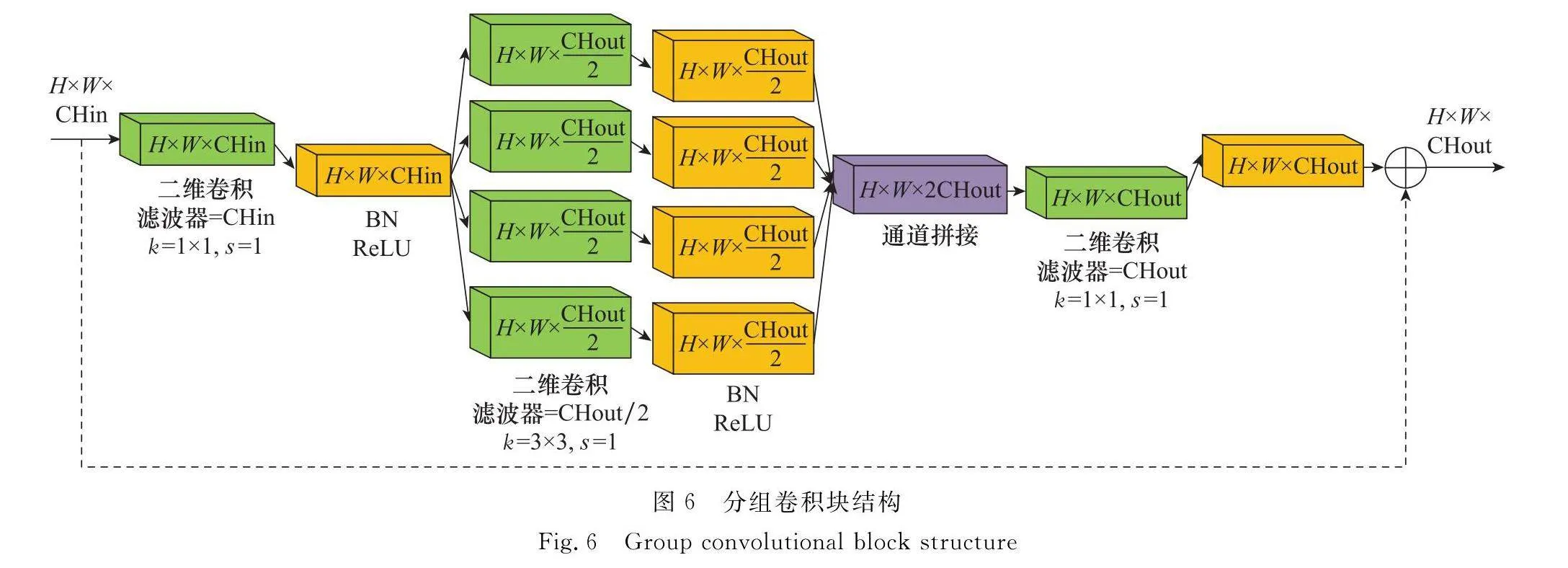
為了獲得較大的感受野，第一個卷積層使用5×5卷積核來提取圖像特征，并且以s=2對圖像進行下采樣，減小圖像尺寸。批歸一化層（batch normalization， BN）將卷積結果歸一化，這樣可以很好地防止網絡過擬合并且加快收斂。平均池化層對特征下采樣減少冗余信息，提高計算效率，增大網絡感受野。Stage 1～Stage 4表示4個分組卷積塊，結構如圖6所示。圖6中，CHin表示分組卷積塊輸入特征圖的通道數。

分組卷積將卷積核拆分為多個組，分別對應輸入特征圖的部分通道卷積，以有效減少模型的參數量。當一個卷積層的輸入通道數為C_i，輸出通道數為C_o，卷積核大小為k×k時，采用分組卷積，分組數為G，參數量為G×（C_i/G）×（C_o/G）×k²，而標準卷積參數量為C_i×C_o×k²。相比于標準卷積，分組卷積的參數量減少為原來的1/G。圖5中每個Stage將原本的3×3卷積分為4組，其參數量變為原來的25%。為保證每個分組卷積在對部分通道卷積的同時考慮不同通道之間的聯系，在分組前采用1×1卷積對輸入特征進行線性變換，建立所有通道之間的聯系。分組的卷積結果拼接后的通道數為2CHout，再次使用1×1卷積進行降維。同時，將殘差結構引入Stage中，通過短連接將輸入添加到輸出中，增加信息熵。在訓練過程中，網絡底層的誤差可以通過殘差結構傳遞到下一層，從而提高網絡的收斂性能，緩解因層數增加引起的梯度消失或梯度爆炸問題。

2 實驗結果與分析

2.1 雷達信號參數仿真設置

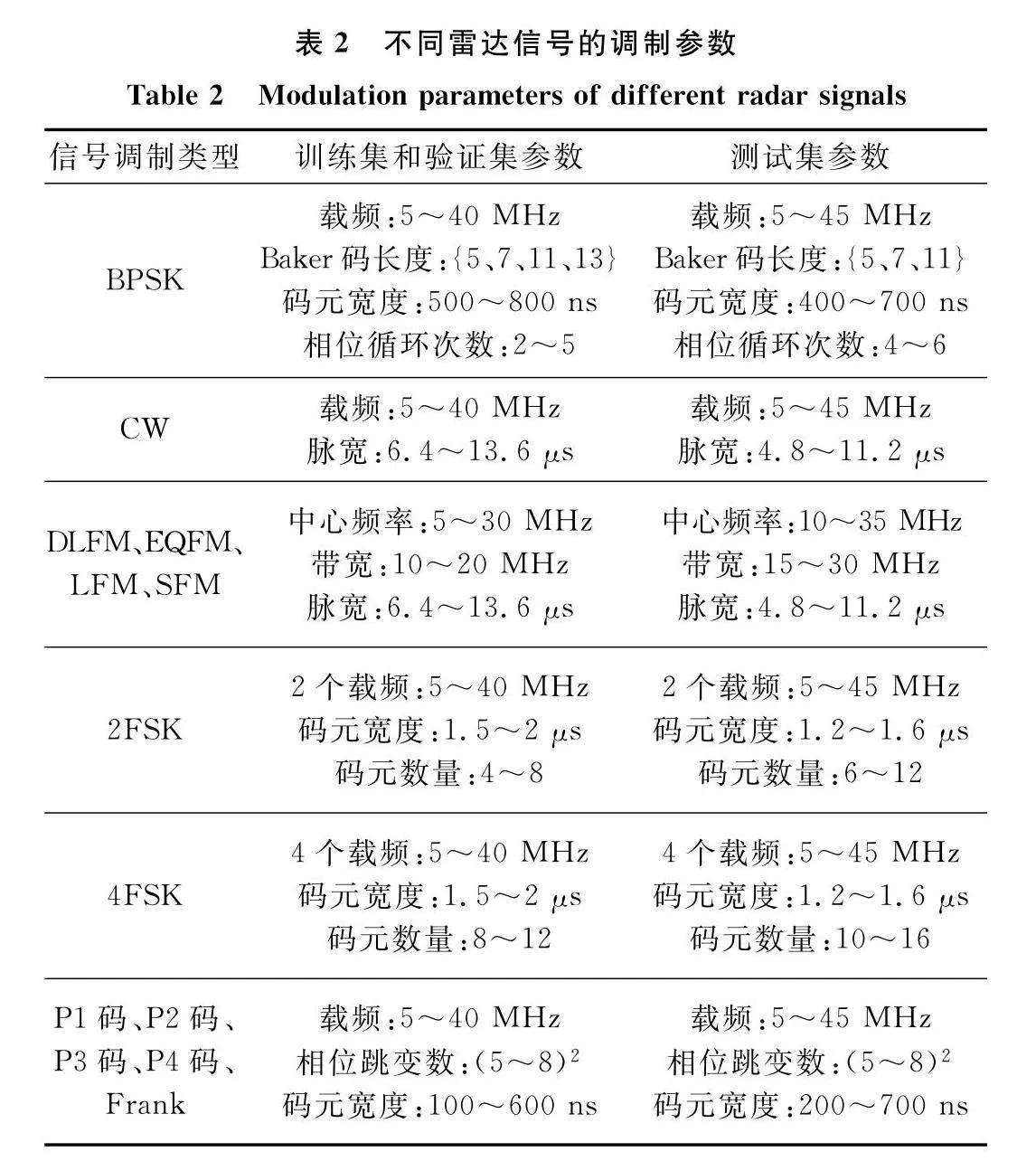
本文采用BPSK（Baker）、CW、DLFM、EQFM、Frank碼、2FSK、4FSK、LFM、P1碼、P2碼、P3碼、P4碼、SFM這13種雷達調制信號來測試識別性能。設置采樣率f_s=100 MHz，信號參數設置如表2所示。

為了更好地衡量網絡的泛化性能，訓練集的信號參數不同于測試集。在訓練集中，每種調制信號的SNR為-8～12 dB，間隔為2 dB。每種調制信號在每個SNR下產生600個

樣本，其中500個樣本用于訓練，100個樣本用于驗證。因此，訓練集中共有7.15萬個樣本，驗證集中共有1.43萬個樣本。在測試集中，每種調制信號SNR為-12～2 dB，間隔為2 dB。每種調制信號在每個SNR下產生200個樣本，測試集中共有2.08萬個樣本。訓練網絡的批量大小為32，初始學習率為1e-3，每迭代10輪，學習率衰減為原來的0.1，迭代40輪后停止訓練，優化器選擇Adam，損失函數為分類交叉熵。

2.2 基于Viterbi算法的SET時頻分布去噪效果分析

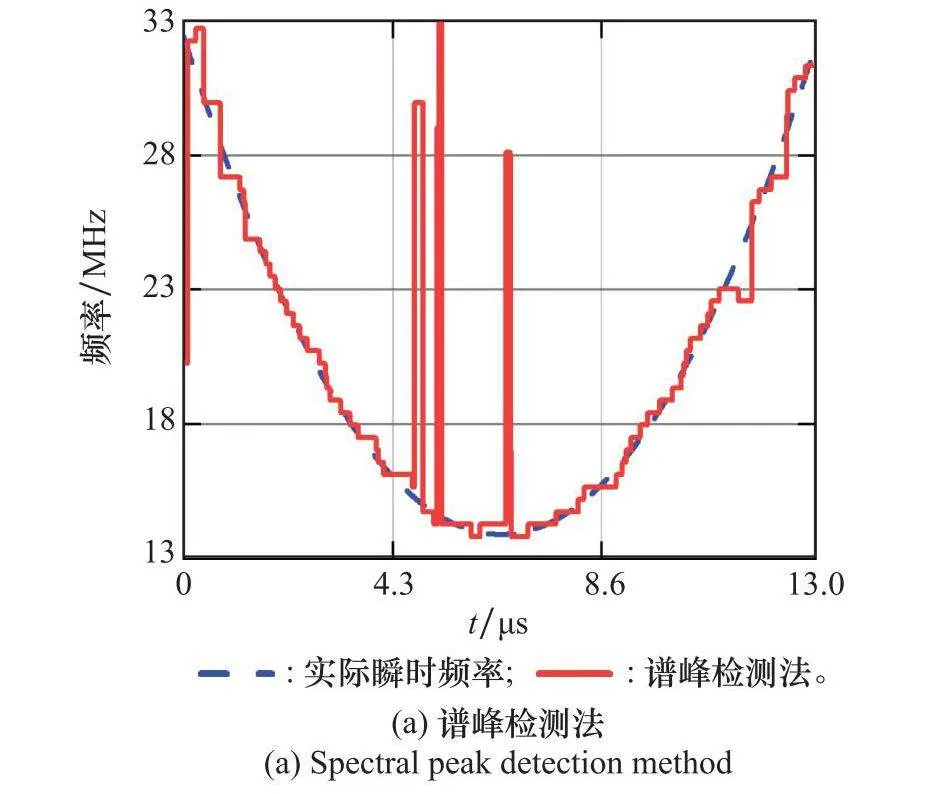
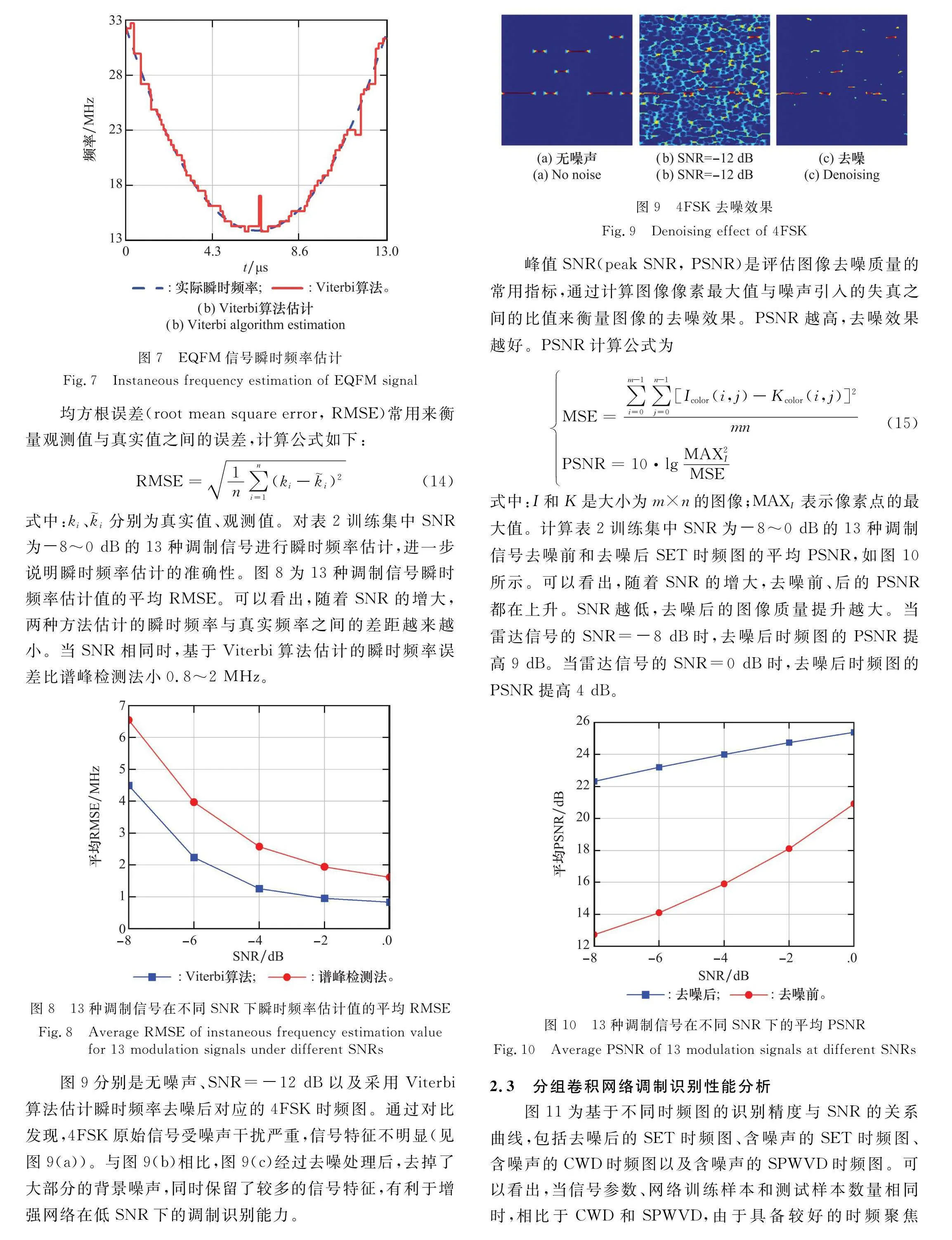
瞬時頻率的估計結果決定時頻圖的去噪效果。瞬時頻率估計最常用的方法是譜峰檢測法，在每個時刻下，將時頻系數矩陣中時頻系數最大值對應的頻率作為該時刻的瞬時頻率^［25］。圖7為SNR=-8 dB時EQFM信號的瞬時頻率估計結果，其中虛線表示信號的實際瞬時頻率。圖7（a）與圖7（b）中的實線分別為基于譜峰檢測法和Viterbi算法估計獲得的瞬時頻率。相對于相譜峰檢測法，Viterbi算法估計同時考慮了每個時刻下時頻系數的最大值以及相鄰時刻瞬時頻率的變化，有效減小了因噪聲引起的瞬時頻率估計誤差，保證頻率估計的準確性。

均方根誤差（root mean square error， RMSE）常用來衡量觀測值與真實值之間的誤差，計算公式如下：

RMSE=1n∑ni=1（k_i-k～_i）²（14）

式中：k_i、k～_i分別為真實值、觀測值。對表2訓練集中SNR為-8～0 dB的13種調制信號進行瞬時頻率估計，進一步說明瞬時頻率估計的準確性。圖8為13種調制信號瞬時頻率估計值的平均RMSE。可以看出，隨著SNR的增大，兩種方法估計的瞬時頻率與真實頻率之間的差距越來越小。當SNR相同時，基于Viterbi算法估計的瞬時頻率誤差比譜峰檢測法小0.8～2 MHz。

圖9分別是無噪聲、SNR=-12 dB以及采用Viterbi算法估計瞬時頻率去噪后對應的4FSK時頻圖。通過對比發現，4FSK原始信號受噪聲干擾嚴重，信號特征不明顯（見圖9（a））。與圖9（b）相比，圖9（c）經過去噪處理后，去掉了大部分的背景噪聲，同時保留了較多的信號特征，有利于增強網絡在低SNR下的調制識別能力。

峰值SNR（peak SNR， PSNR）是評估圖像去噪質量的常用指標，通過計算圖像像素最大值與噪聲引入的失真之間的比值來衡量圖像的去噪效果。PSNR越高，去噪效果越好。PSNR計算公式為

MSE=∑m－1i=0∑n－1j=0［I_color（i，j）－K_color（i，j）］²mn

PSNR=10·lgMAX²_IMSE（15）

式中：I和K是大小為m×n的圖像;MAXI表示像素點的最大值。計算表2訓練集中SNR為-8～0 dB的13種調制信號去噪前和去噪后SET時頻圖的平均PSNR，如圖10所示。可以看出，隨著SNR的增大，去噪前、后的PSNR都在上升。SNR越低，去噪后的圖像質量提升越大。當雷達信號的SNR=-8 dB時，去噪后時頻圖的PSNR提高9 dB。當雷達信號的SNR=0 dB時，去噪后時頻圖的PSNR提高4 dB。

2.3 分組卷積網絡調制識別性能分析

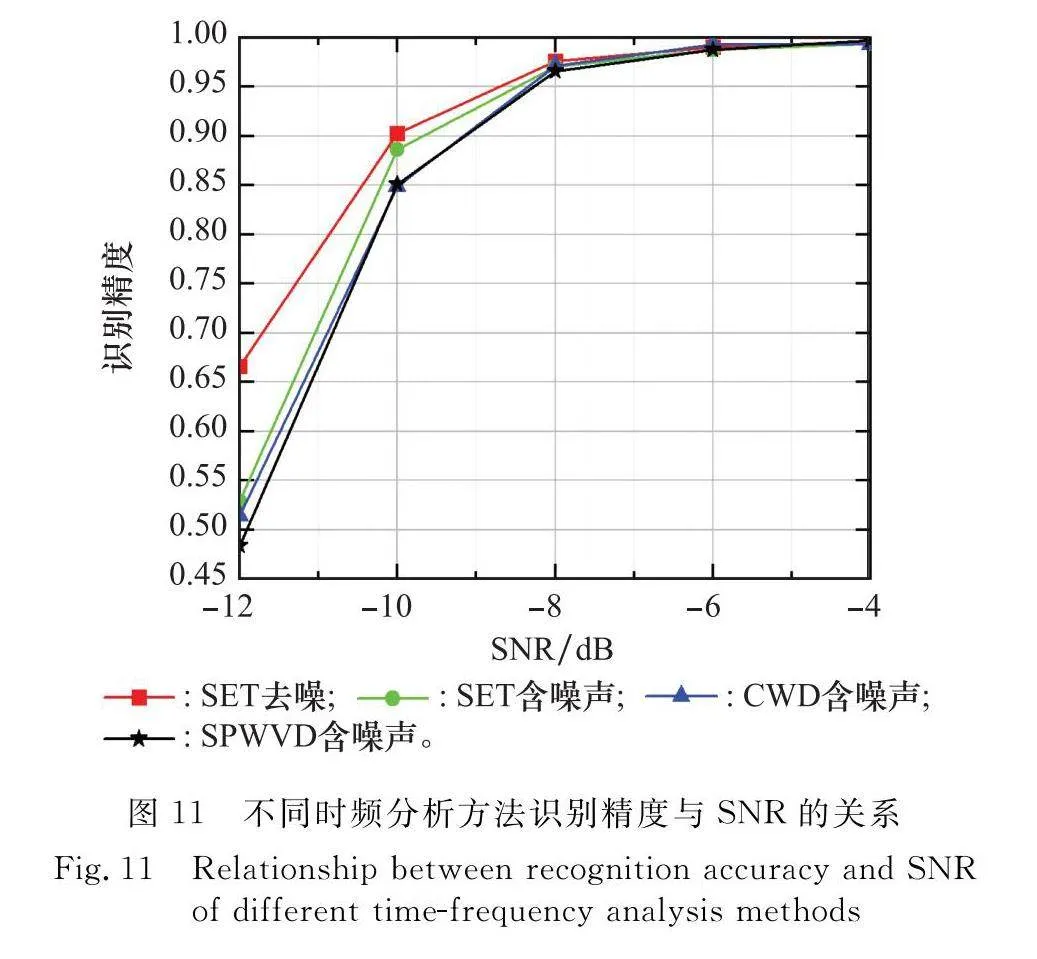
圖11為基于不同時頻圖的識別精度與SNR的關系曲線，包括去噪后的SET時頻圖、含噪聲的SET時頻圖、含噪聲的CWD時頻圖以及含噪聲的SPWVD時頻圖。可以看出，當信號參數、網絡訓練樣本和測試樣本數量相同時，相比于CWD和SPWVD，由于具備較好的時頻聚焦性，SET時頻曲線具有更高的清晰度以及識別精度。當SNR=-12 dB時，去噪后的SET時頻圖識別精度相比去噪前提升了13.69%。隨著SNR的提高，噪聲對信號時頻分布的干擾越小，去噪前、后的SET時頻圖識別精度差距逐漸減小。

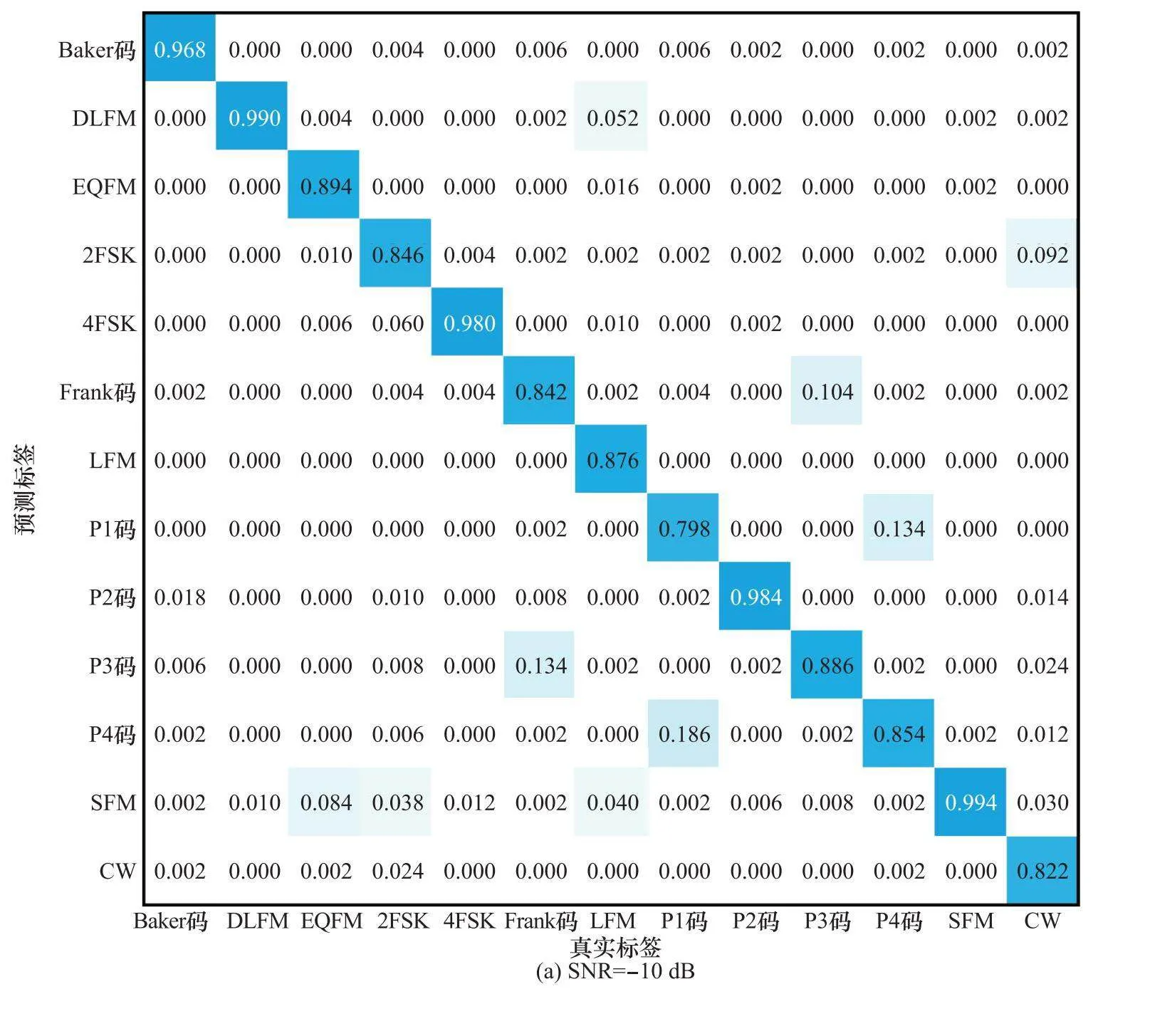
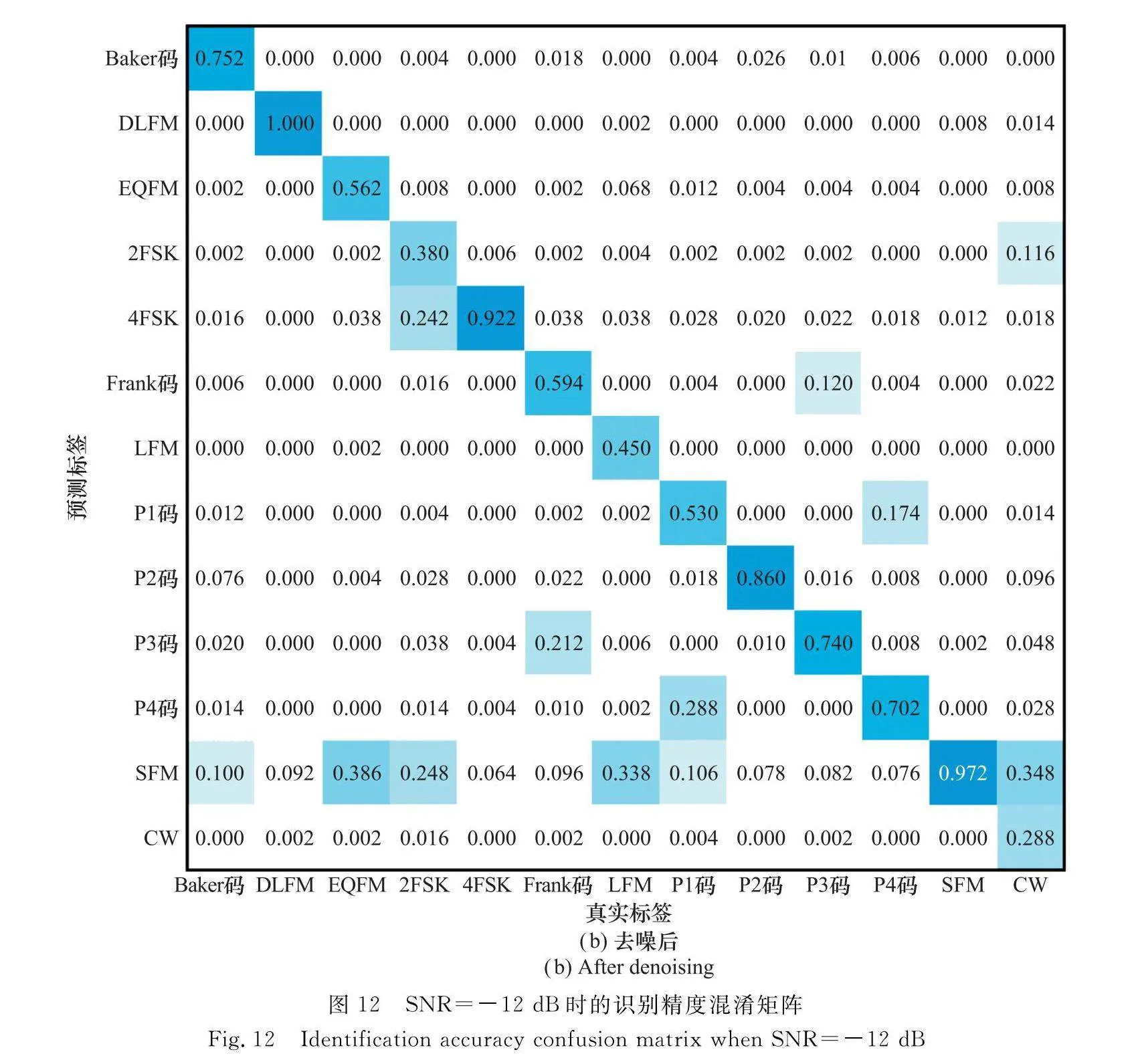
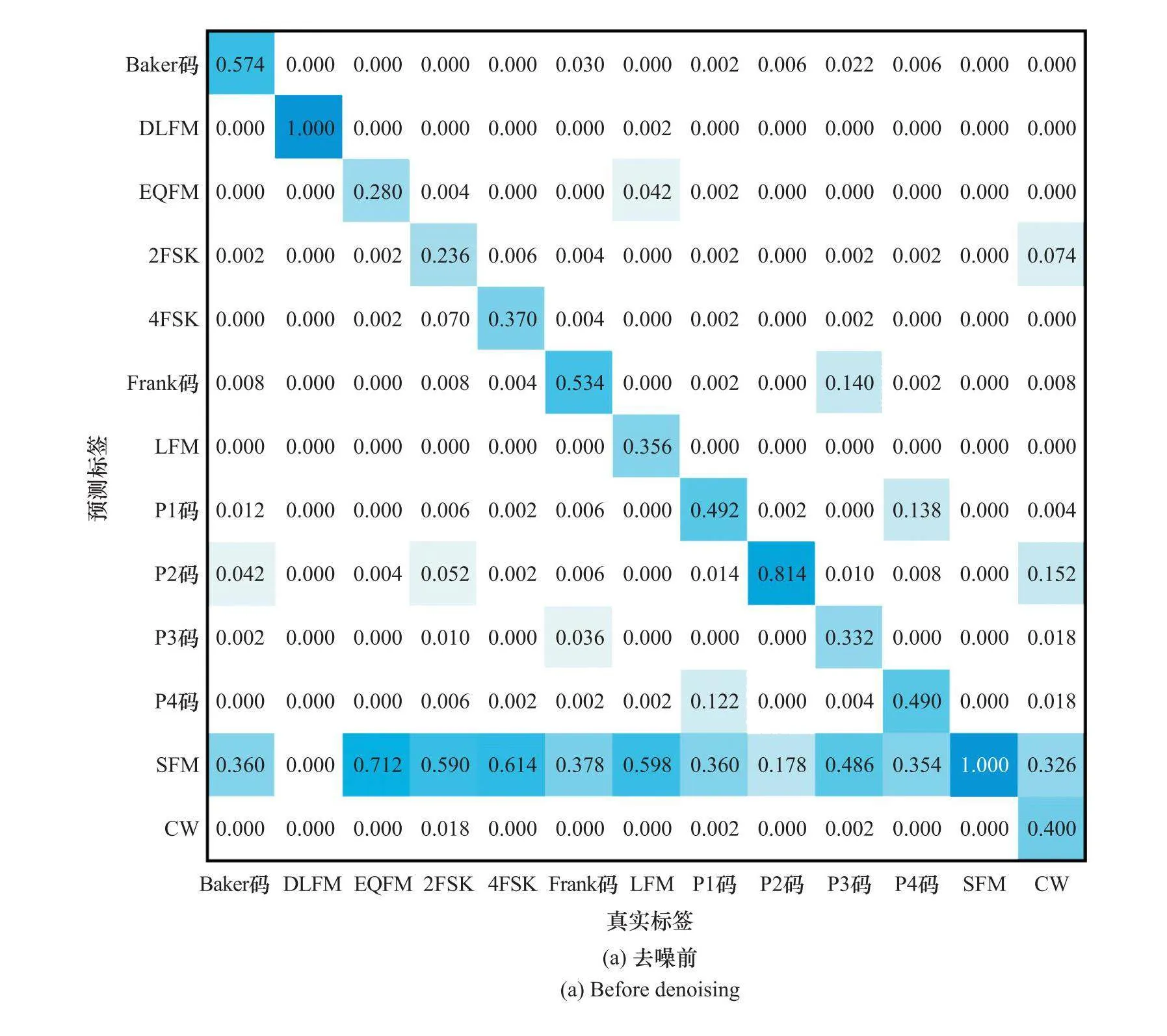
為了進一步分析所提算法在低SNR下的識別性能，圖12為基于SET時頻分析方法在去噪前、去噪后的識別精度混淆矩陣（SNR=-12 dB）。從圖12（a）可以看出，去噪前時頻圖的調制方式容易被誤識別為SFM。由于SNR較低，信號時頻特征受噪聲干擾影響較大，不同調制方式之間的特征差異變小，不同調制類型的時頻圖在訓練過程中被認為是同一種調制類型，導致網絡擅長識別某幾種調制方式，而其他的調制方式識別精度很差。時頻圖去噪后去掉了大部分噪聲，較好地保留了信號特征，增強了不同調制類型的差異性，從而提高了調制信號整體的識別精度。從圖12（b）可以看出，4FSK、P3碼和EQFM在去噪后識別精度分別提高了55.2%、40.8%和28.2%。去噪后被誤識別為SFM的概率有效下降，P4碼和Baker被誤識別為SFM的概率分別下降了27.8%和26%。

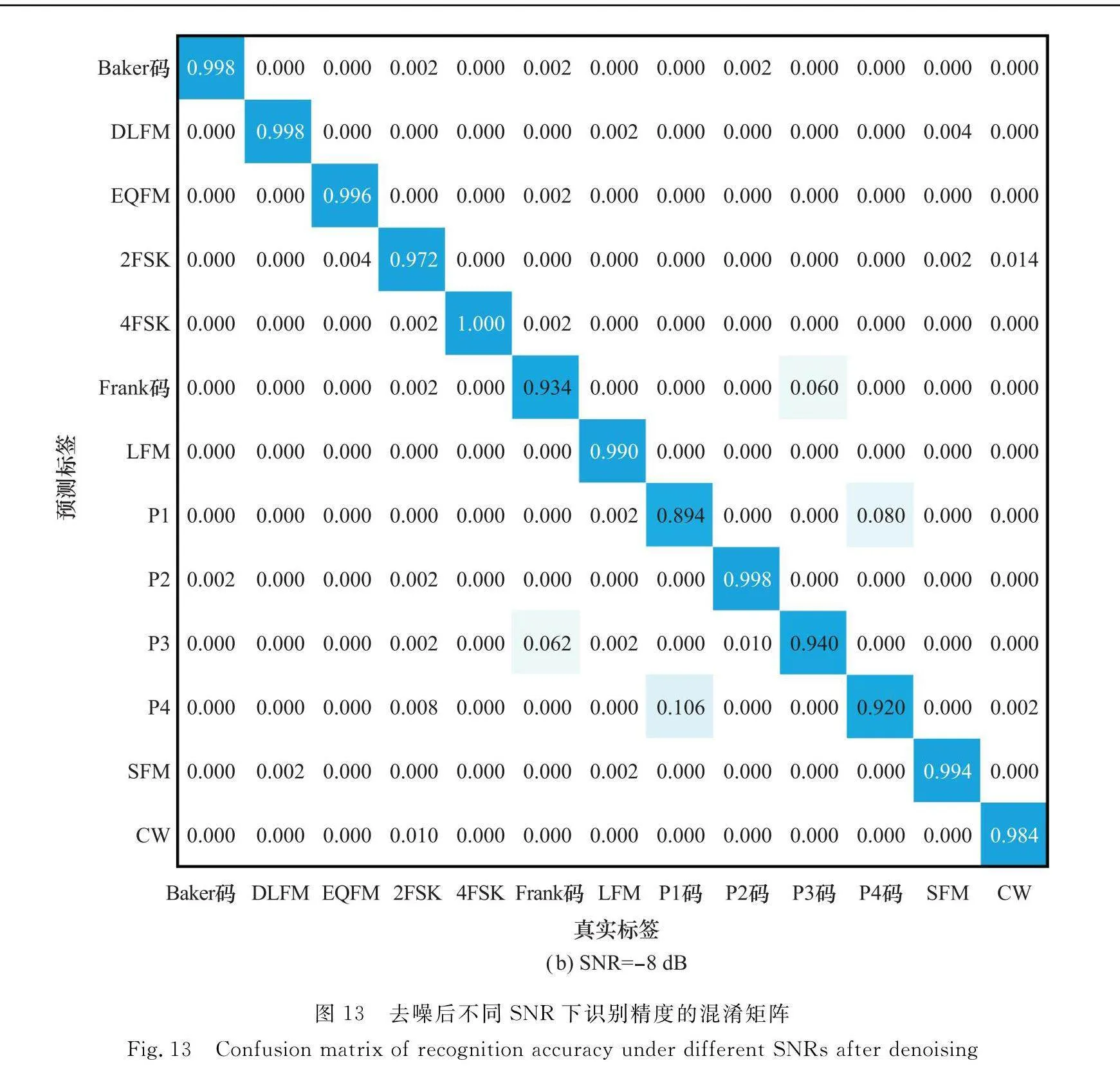
為了更好地分析調制識別精度隨SNR的變化，圖13給出了基于SET的時頻分析方法在去噪后不同SNR下識別精度的混淆矩陣。當SNR分別為-10 dB和-8 dB時，去噪后的13種調制信號的平均識別精度分別為90.26%和97.63%。隨著SNR的提升，時頻圖受噪聲影響逐漸減小，識別精度逐漸上升。與圖12（b）相比，其他調制信號被誤識別為SFM的概率下降了一個數量級。由于CW調制抗噪聲性能較差，在SNR提升后其識別精度明顯上升。2FSK與4FSK時頻圖相似，在SNR提升后，2FSK被混淆為4FSK的概率從24.2%降低至6.0%。

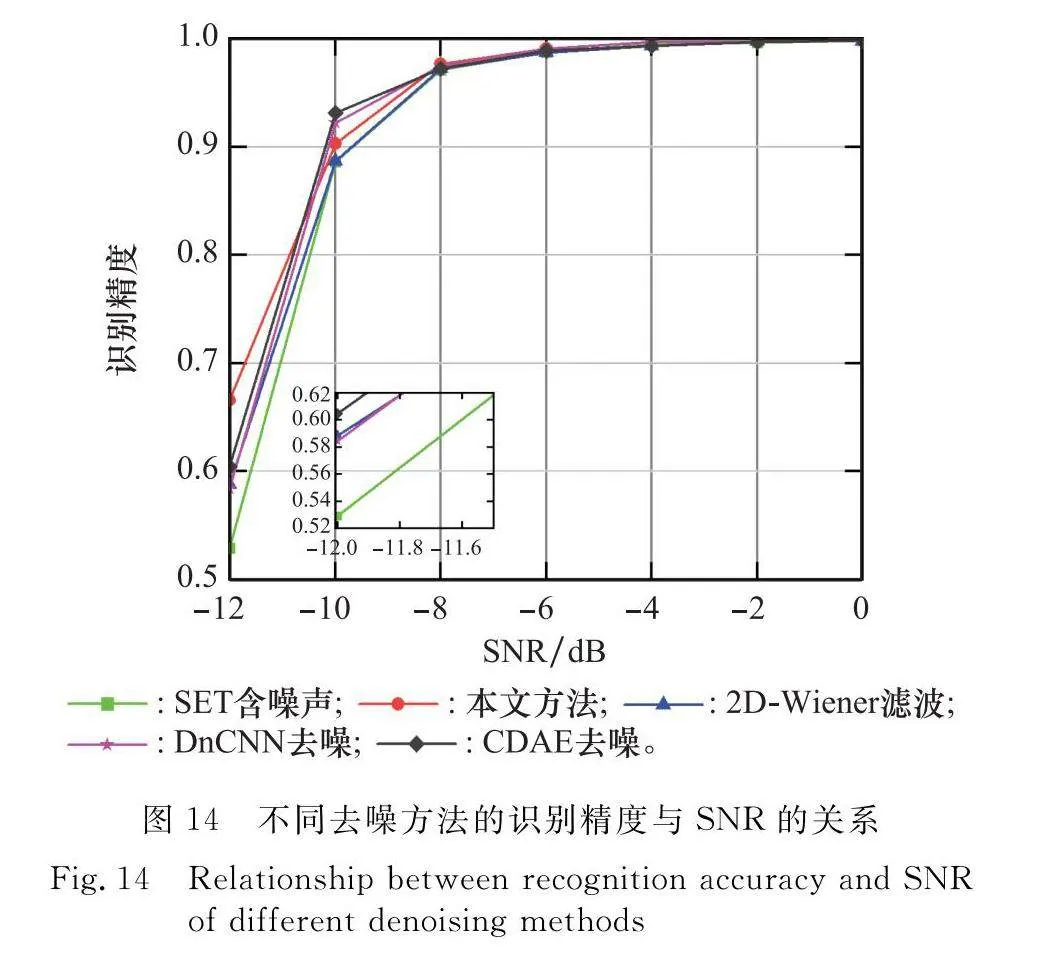
隨著SNR的降低，時頻圖中的信號軌跡逐漸模糊，信號的能量分布逐漸淹沒在噪聲中。根據文獻［2628］，二維自適應維納（two-dimensional adaptive Wiener， 2D-Wiener）濾波、前饋去噪CNN（denoising CNN， DnCNN）和卷積去噪自編碼器（convolution denoising autoencoder， CDAE）在噪聲抑制方面具有良好的性能。圖14給出了4種去噪方法的識別精度與SNR的關系曲線。可以看出，當SNR為-12 dB時，經本文方法去噪后識別精度提高13.69%，2D-Wiener、DnCNN、CDAE這3種方法去噪后的識別精度分別提高了5.91%、5.54%、7.54%，識別精度均低于本文方法;當SNR為-10 dB時，本文方法去噪后識別精度提高1.65%，2D-Wiener、DnCNN、CDAE這3種方法去噪后的識別精度分別提高0.038%、3.59%、4.52%，DnCNN和CDAE去噪后的識別精度優于本文。這是由于SNR提高后，信號的能量特征變清晰，DnCNN和CDAE能較好地學習信號能量特征，從而實現較好的去噪效果，但是這兩種去噪網絡需要無噪聲或者SNR較高的時頻圖來訓練網絡參數，而實際環境中偵察接收機截獲的信號包含大量的噪聲，并且當信號種類發生變化之后，去噪模型需要重新訓練，實用性較差。本文所提方法通過估計時頻圖中信號的瞬時頻率軌跡達到去噪的效果，無需純凈的時頻圖來訓練去噪模型，實用性較好。

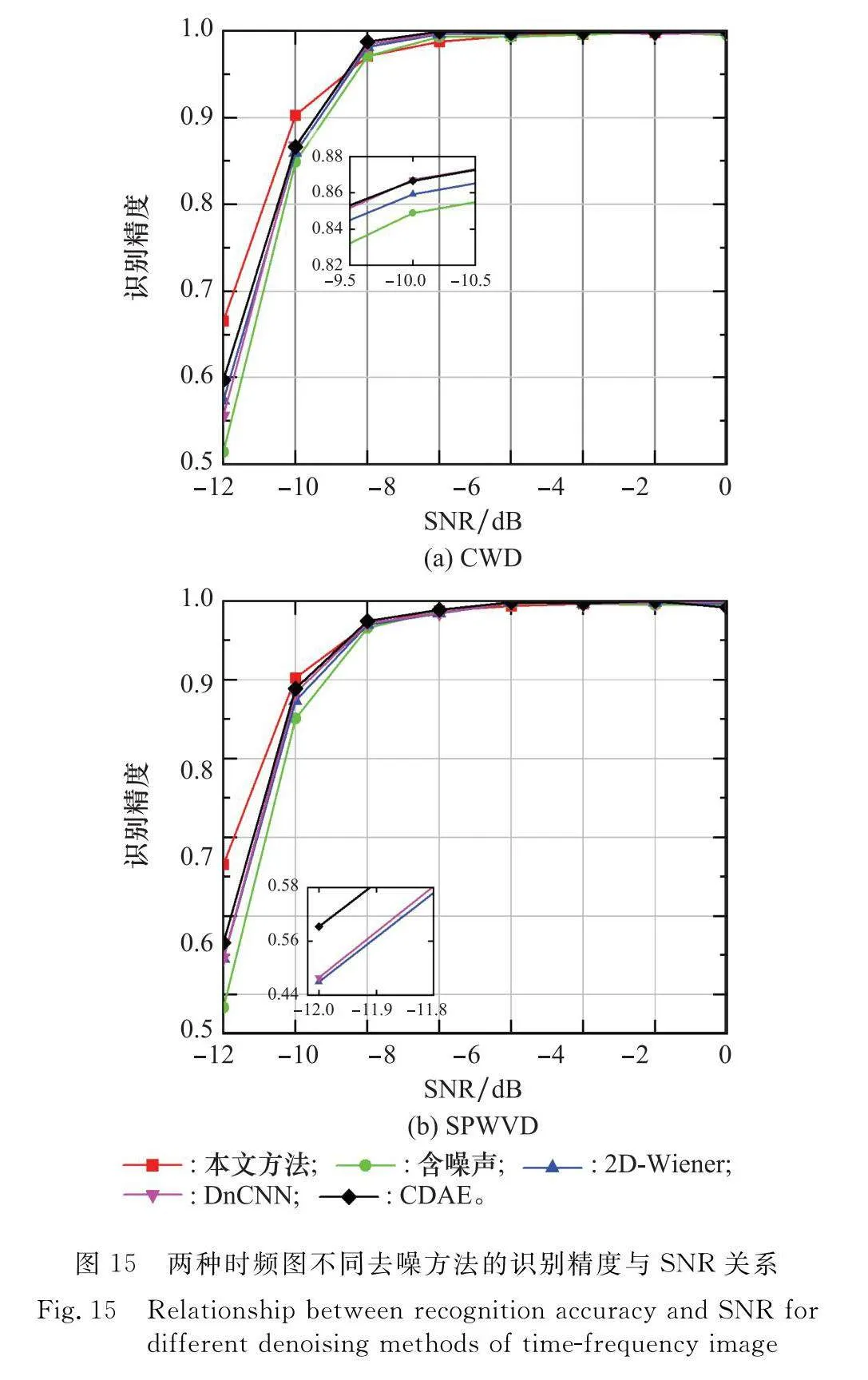
同樣地，2D-Wiener濾波、DnCNN和CDAE也可用于CWD和SPWVD時頻圖的去噪。圖15為CWD、SPWVD時頻圖不同去噪方法的識別精度與SNR的關系。從圖15（a）中可以看出，當SNR=-12 dB時，2D-Wiener、DnCNN、CDAE這3種方法去噪后CWD時頻圖識別精度分別提高5.96%、4.12%、8.27%;當SNR=-10 dB時，CWD時頻圖去噪后的識別精度分別提高1.04%、1.85%、1.78%。從圖15（b）中可以看出，當SNR=-12 dB時，2D-Wiener、DnCNN、CDAE這3種方法去噪后的SPWVD時頻圖識別精度分別提高6.15%、6.31%、8.19%;當SNR=-10 dB時，SPWVD時頻圖去噪后的識別精度分別提高2.23%、3.23%、3.81%。使用這3種方法去噪后的CWD、SPWVD時頻圖的識別精度均有不同程度的提高，但是均低于本文基于SET的去噪法。這是因為在相同的條件下，SET相對于CWD、SPWVD具有更好的時頻聚焦性，時頻圖中信號的能量軌跡也更清晰，相比之下具有更好的去噪效果。

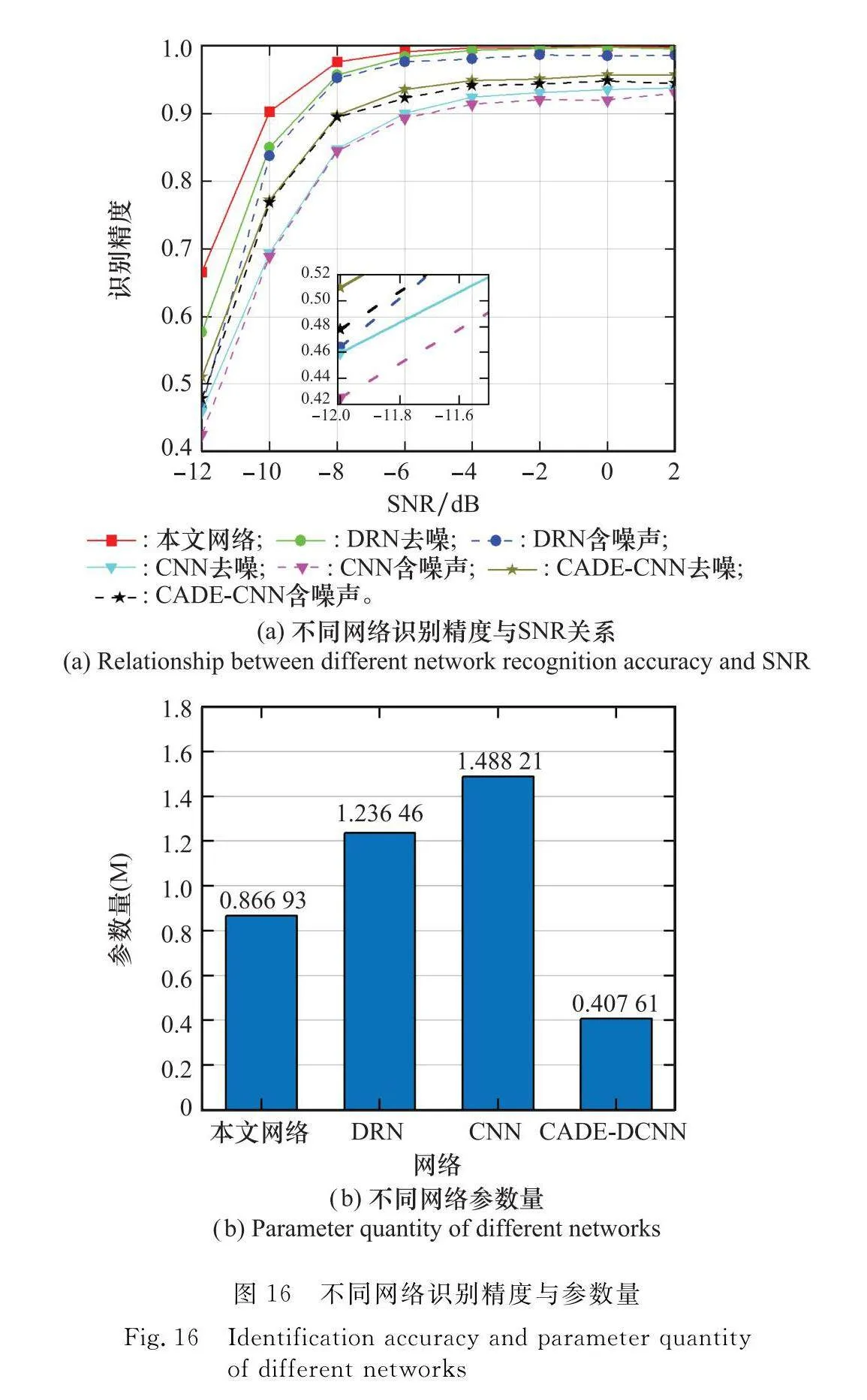
為了更客觀地評估去噪性能和網絡的識別性能，分別與文獻［29］提出的（dilated residual network， DRN）、文獻［30］提出的CNN以及文獻［31］提出的CADE-深度CNN（deep CNN， DCNN）進行比較，結果如圖16所示。本文網絡表示使用基于分組卷積的神經網絡對去噪后的SET時頻圖識別效果，DRN去噪表示使用DRN對去噪后的SET時頻圖的識別結果，DRN含噪聲表示使用DRN對去噪前的SET時頻圖的識別結果。可以看出，針對不同網絡，去噪后的SET時頻圖的識別精度均有所提升。當SNR=-12 dB時，相較于去噪前，DRN、CNN以及CADE-DCNN的識別精度分別提高11.25%、3.45%和3.18%。這3種網絡的識別精度均低于本文提出的分組卷積網絡。圖16（b）為不同網絡的參數量對比，CNN的參數量最多，約為1.5 M（1 M=1e6），CADE-DCNN的參數量最少，約為0.4 M。得益于分組卷積和殘差連接，本文提出的分組卷積網絡能夠在不損失識別精度的前提下有效減少網絡參數。

2.4 消融實驗

本文使用一種基于殘差連接分組的CNN對雷達信號的時頻圖進行識別，為了驗證分組卷積塊參數設置對識別精度的影響，首先測試分組卷積中分組數d對整個網絡識別精度的影響。從表3可以看出，增大分組數d可以減少模型的參數量。當SNR=-12 dB，d=4時，識別精度最高。這是因為當分組數較少時，模型參數量多，模型可以在訓練樣本和目標之間完美映射，但是這種映射缺乏泛化能力;當分組數較多時，模型參數量減少，模型的映射能力減弱，識別精度下降。

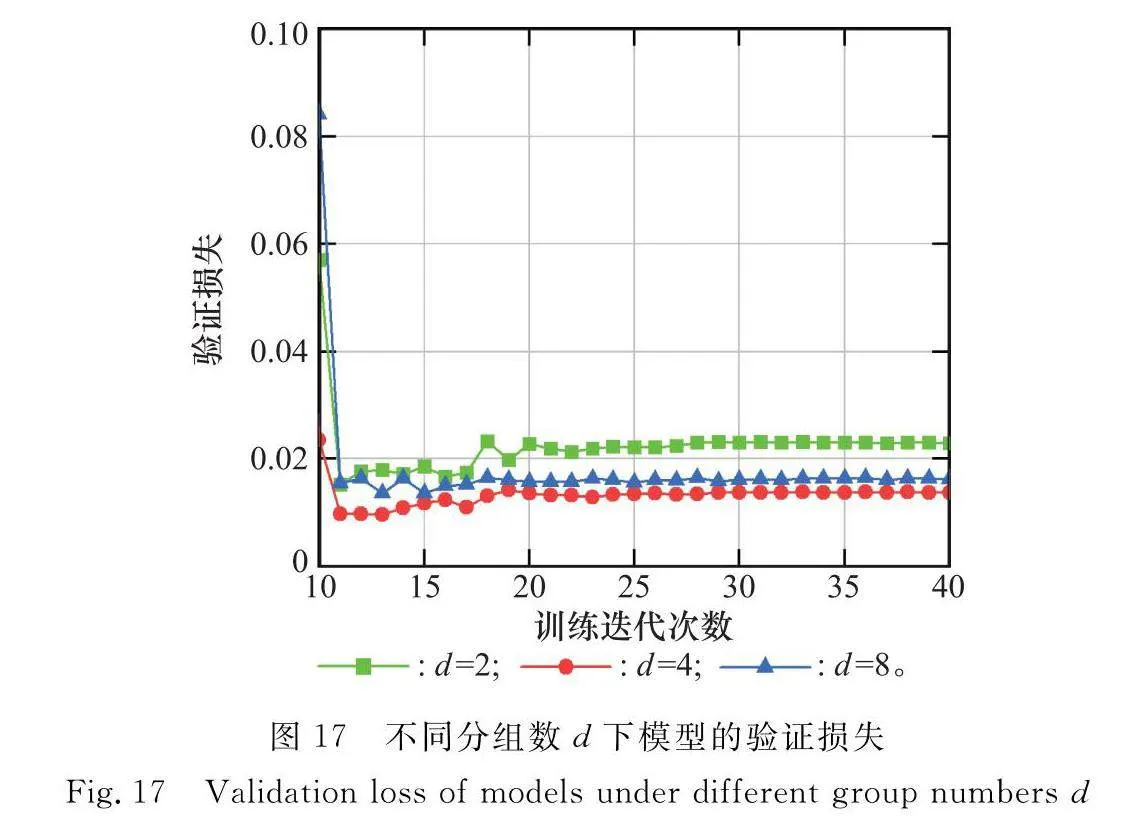
圖17是不同分組數d下模型在訓練過程中的驗證損失。可以看出，當d=4時，模型最終的驗證損失收斂值最低。驗證損失越低，代表模型的泛化能力越好。圖17中不同分組下驗證損失的收斂趨勢與表3中的識別準確率變化趨勢相同。因此，最終選擇d=4作為分組卷積中的分組數。

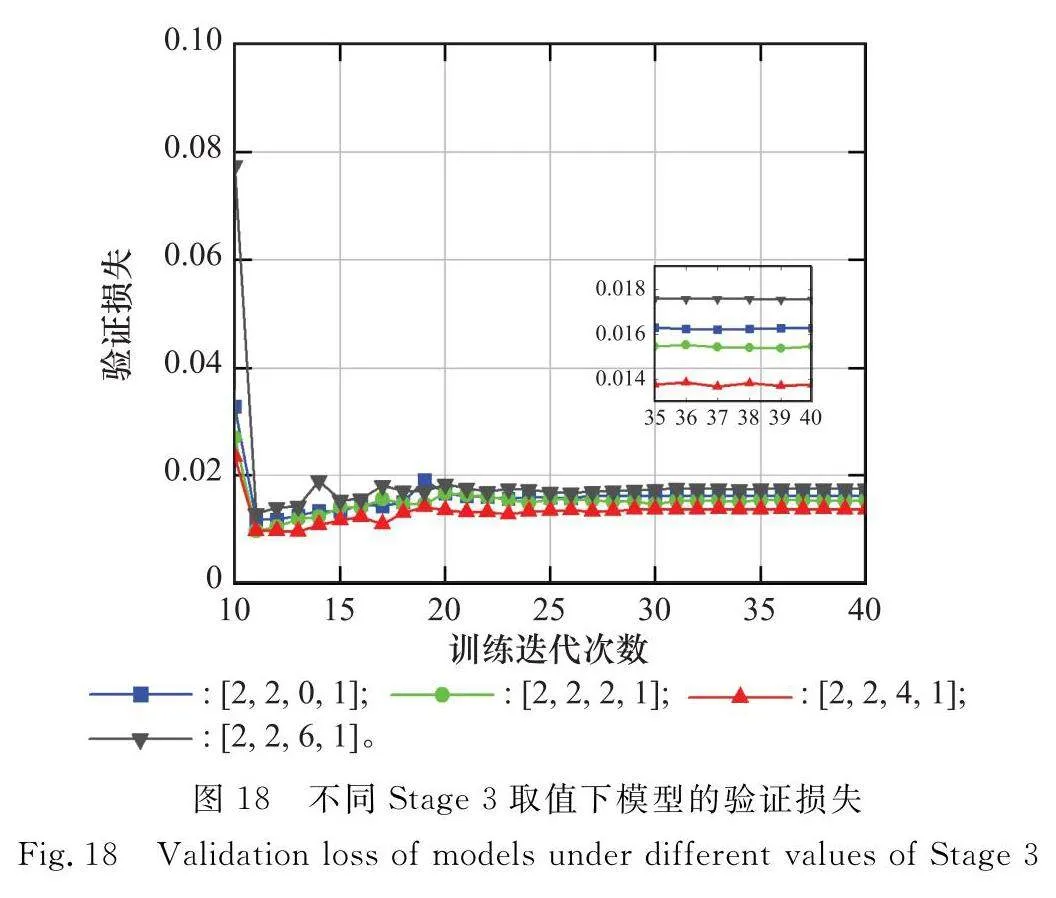
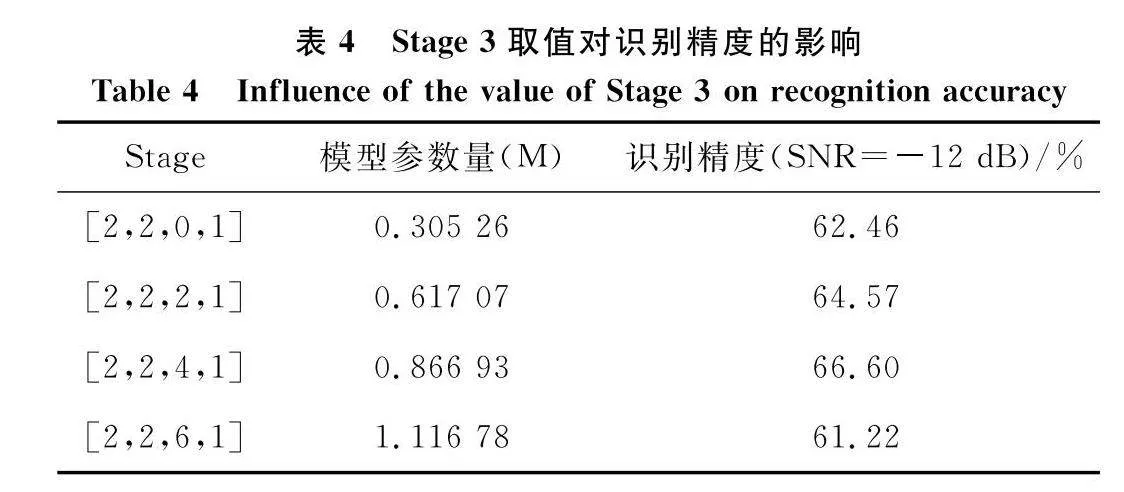
以分組卷積塊Stage 3為例，改變Stage 3的個數，網絡的識別精度如表4所示。當Stage 3的個數為0時，表示網絡中取消第3組分組卷積塊。當Stage 3的個數從0開始逐漸增加時，網絡參數量逐漸增多，SNR=-12 dB時的識別精度先上升后下降。這是因為當網絡參數逐漸增加時，網絡逐漸從欠擬合狀態變為過擬合狀態。當Stage 3為4時，識別精度最高。

圖18為不同Stage 3取值下網絡的驗證損失。可以看出，當Stage 3為4時，驗證損失收斂值最低;當Stage 3為6時，驗證損失收斂值最高。圖18的驗證損失收斂值與表4的識別精度相吻合，因此最終選擇Stage 3=4。

3 結 論

本文提出了一種基于SET分組CNN的調制識別方法，能有效解決低SNR下雷達信號調制識別準確率低的問題。利用SET時頻分布獲得13種雷達信號的時頻系數矩陣，結合Viterbi算法和中值濾波提取信號的瞬時頻率并保留其鄰域的時頻系數以實現去噪，最后使用分組CNN對去噪圖像進行分類識別。相比于常用的CWD和SPWVD時頻分布，SET時頻變換計算復雜度顯著降低，其計算耗時分別為CWD的27%、SPWVD的24%。所提出的Viterbi-SET時頻圖去噪算法有效提高了低SNR下時頻圖的圖像質量，當雷達信號的SNR=0 dB時，去噪后時頻圖的PSNR提高了9 dB。基于殘差連接的分組卷積網絡在保證識別精度的前提下減少了網絡參數，降低了網絡在邊緣設備的部署難度，分組數為4的卷積參數量僅為傳統卷積的25%。實驗結果表明，當SNR=-12 dB時，去噪后的時頻圖在4種不同的網絡結構中識別精度均有不同程度的提高，分別提高13.69%、11.25%、3.45%和3.18%。所提出的雷達信號調制識別方法在低SNR條件下對多種復雜調制類型的信號具有良好的識別性能。

參考文獻

［1］ ISMAIL G U L， ISLN E. Randomized low rank and sparse decomposition based receiver search strategy for electronic support receivers［J］. IEEE Trans.on Aerospace and Electronic Systems， 202 59（2）： 13921399.

［2］ XU X S， BI D P， PAN J F， et al. An end-to-end deep learning approach for state recognition of multifunction radars［J］. Sensors， 202 22（13）： 4980.

［3］ PARK B， AHN J M. Intra-pulse modulation recognition using pulse description words and complex waveforms［C］∥Proc.of the International Conference on Information and Communication Technology Convergence， 2017： 555560.

［4］ ZHU M T， LI Y J， WANG S F. Model-based time series clustering and interpulse modulation parameter estimation of multifunction radar pulse sequences［J］. IEEE Trans.on Aerospace and Electronic Systems， 202 57（6）： 36733690.

［5］ ZHANG X L， ZHANG J Z， LUO T Z， et al. Radar signal intrapulse modulation recognition based on a denoising-guided disentangled network［J］. Remote Sensing， 202 14（5）： 1252.

［6］ XU J L， SU W， ZHOU M C. Likelihood-ratio approaches to automatic modulation classification［J］. IEEE Trans.on Systems， Man， and Cybernetics， Part C （Applications and Reviews）， 2010， 41（4）： 455469.

［7］ HAMEED F， DOBRE O A， POPESCU D C. On the likelihood-based approach to modulation classification［J］. IEEE Trans.on Wireless Communications， 2009， 8（12）： 58845892.

［8］ RAMEZANI-KEBRYA A， KIM I M， KIM D I， et al. Likelihood-based modulation classification for multiple-antenna receiver［J］. IEEE Trans.on Communications， 2013， 61（9）： 38163829.

［9］ ZHANG J W， CABRIC D， WANG F G， et al. Cooperative modulation classification for multipath fading channels via expectation-maximization［J］. IEEE Trans.on Wireless Communications， 2017， 16（10）： 66986711.

［10］ 李正權， 林媛， 李夢雅， 等. 基于判別式受限玻爾茲曼機的數字調制識別［J］. 通信學報， 202 42（2）： 8191.

LI Z Q， LIN Y， LI M Y， et al. Digital modulation recognition based on discriminative restricted Boltzmann machine［J］. Journal on Communications， 202 42（2）： 8191.

［11］ RU X H， LIU Z， JIANG W L， et al. Recognition performance analysis of instaneous phase and its transformed features for radar emitter identification［J］. IET Radar， Sonar amp; Navigation， 2016， 10（5）： 945952.

［12］ CHENG Y Q， GUO M R， GUO L M. Radar signal recognition exploiting information geometry and support vector machine［J］. IET Signal Processing， 2023， 17（1）： e12167.

［13］ ASLAM M W， ZHU Z C， NANDI A K. Automatic modulation classification using combination of genetic programming and KNN［J］. IEEE Trans.on Wireless Communications， 201 11（8）： 27422750.

［14］ CHEN K Y， ZHU L Z， CHEN S， et al. Deep residual learning in modulation recognition of radar signals using higher-order spectral distribution［J］. Measurement， 202 185： 109945.

［15］ WEI S J， QU Q Z， SU H， et al. Intra-pulse modulation radar signal recognition based on CLDN network［J］. IET Radar， Sonar amp; Navigation， 2020， 14（6）： 803810.

［16］ ZHU Z G， JI H B， ZHANG W B， et al. Complex convolutional neural network for signal representation and its application to radar emitter recognition［J］. IEEE Communications Letters， 2023， 27（3）： 856860.

［17］ YUAN S B， WU B， LI P. Intra-pulse modulation classification of radar emitter signals based on a 1-D selective kernel convolutional neural network［J］. Remote Sensing， 202 13（14）： 2799.

［18］ LI D J， YANG R J， LI X B， et al. Radar signal modulation recognition based on deep joint learning［J］. IEEE Access， 2020， 8： 4851548528.

［19］ LIAO Y P， JIANG F， WANG J L. Intra-pulse modulation recognition of radar signals based on multi-feature random matching fusion network［J］. The Journal of Supercomputing， 2023， 79（6）： 64226451.

［20］ ZHANG Z F， WANG C， GAN C Q， et al. Automatic modulation classification using convolutional neural network with features fusion of SPWVD and BJD［J］. IEEE Trans.on Signal and Information Processing over Networks， 2019， 5（3）： 469478.

［21］ 郭立民， 寇韻涵， 陳濤， 等. 基于棧式稀疏自編碼器的低信噪比下低截獲概率雷達信號調制類型識別［J］. 電子與信息學報， 2018， 40（4）： 875881.

GUO L M， KOU Y H， CHEN T， et al. Low probability of intercept radar signal recognition based on stacked sparse auto-encoder［J］. Journal of Electronics amp; Information Technology， 2018， 40（4）： 875881.

［22］ 邵凱， 朱苗苗， 王光宇. 基于生成對抗與卷積神經網絡的調制識別方法［J］. 系統工程與電子技術， 202 44（3）： 10361043.

SHAO K， ZHU M M， WANG G Y. Modulation recognition method based on generative adversarial and convolutional neural network［J］. Systems Engineering and Electronics， 202 44（3）： 10361043.

［23］ OBERLIN T， MEIGNEN S， PERRIER V. The Fourier-based synchrosqueezing transform［C］∥Proc.of the IEEE International Conference on Acoustics， Speech and Signal Processing， 2014： 315319.

［24］ YU G， YU M J， XU C Y. Synchroextracting transform［J］. IEEE Trans.on Industrial Electronics， 2017， 64（10）： 80428054.

［25］ MAO W T， CHEN J X， LIANG X H， et al. A new online detection approach for rolling bearing incipient fault via self-adaptive deep feature matching［J］. IEEE Trans.on Instrumentation and Measurement， 2019， 69（2）： 443456.

［26］ SI W J， WAN C X， DENG Z A. Intra-pulse modulation recognition of dual-component radar signals based on deep convolutional neural network［J］. IEEE Communications Letters， 202 25（10）： 33053309.

［27］ YU H H， YAN X P， LIU S K， et al. Radar emitter multi-label recognition based on residual network［J］. Defence Technology， 202 18（3）： 410417.

［28］ HOU C B， FU D Y， HUA L J， et al. The recognition of multi-components signals based on semantic segmentation［J］. Wireless Networks， 2023， 29（1）： 147160.

［29］ 秦鑫， 黃潔， 查雄， 等. 基于擴張殘差網絡的雷達輻射源信號識別［J］. 電子學報， 2020， 48（3）： 456462.

QIN X， HUANG J， ZHA X， et al. Radar emitter signal recognition based on dilated residual network［J］. Acta Electronica Sinica， 2020， 48（3）： 456462.

［30］ QU Z Y， MAO X J， DENG Z A. Radar signal intra-pulse modulation recognition based on convolutional neural network［J］. IEEE Access， 2018， 6： 4387443884.

［31］ QU Z Y， WANG W Y， HOU C B， et al. Radar signal intra-pulse modulation recognition based on convolutional denoising autoencoder and deep convolutional neural network［J］. IEEE Access， 2019， 7： 112339112347.

作者簡介

鄧志安（1985—），男，教授，博士，主要研究方向為人工智能、寬帶信號處理。

王治國（1999—），男，碩士研究生，主要研究方向為雷達信號調制識別。

王盛鰲（1983—），男，高級工程師，碩士，主要研究方向為信號處理與目標識別。

司偉建（1971—），男，研究員，博士，主要研究方向為寬帶信號處理、電子偵察。