帶殘余頻偏的軟擴頻信號偽碼序列盲估計



摘 要:針對帶殘余頻偏的軟擴頻信號偽碼序列盲估計難的問題,提出一種奇異值分解(singular value decomposition, SVD)結合全數字鎖相環(digital phase locked loop, DPLL)的方法。所提方法首先對待處理信號通過不重疊分段生成數據矩陣,每段信號長度為一倍偽碼周期;然后利用其自相關矩陣的右上角元素估計失步點進行同步,并且在重新計算自相關矩陣后根據較大特征值個數估計進制數;最后通過多次快速SVD算法結合DPLL最終實現偽碼序列的盲估計。仿真結果顯示,所提方法在低信噪比條件下可以有效估計出帶殘余頻偏的軟擴頻信號的偽碼序列,并且性能優于其他對比方法。
關鍵詞: 軟擴頻信號; 盲估計; 殘余頻偏; 奇異值分解; 全數字鎖相環
中圖分類號: TN 911.7 文獻標志碼: A""" DOI:10.12305/j.issn.1001-506X.2024.10.35
Blind estimation of pseudo-code sequence of soft spread spectrum
signal with residual frequency offset
ZHANG Tianqi, ZHANG Huizhi LUO Qingyu, FANG Rong
(School of Communication and Information Engineering, Chongqing University of Posts and
Telecommunications, Chongqing 400065, China)
Abstract: Aiming at the difficulty of blind estimation of pseudo-code sequence of soft spread spectrum signals with residual frequency offset, a singular value decomposition (SVD) combined with digital phase locked loop (DPLL) method is proposed. The data matrix is generated through non-overlapping segments of the signal to be processed, and the length of each segment is a single pseudo-code period. Then, the element in the upper right corner of the autocorrelation matrix is used to estimate the out-of-step point for synchronization, and the autocorrelation matrix is recalculated to estimate the base number according to the number of large eigenvalues. Finally, the blind estimation of pseudo-code sequence is finally realized by combining multiple fast SVD algorithms with DPLL. The simulation results show that the proposed method can effectively estimate the pseudo-code sequence of the soft spread spectrum signal with residual frequency offset under low signal-to-noise ratio (SNR), and the performance of the proposed method is better than that of other comparative methods.
Keywords: soft spread spectrum signal; blind estimation; residual frequency offset; singular value decomposition (SVD); digital phase locked loop (DPLL)
0 引 言
軟擴頻信號是直接序列擴頻(direct-sequence spread spectrum, DSSS)技術和編碼技術相結合所形成的一種直擴通信信號[1]。在保留了DSSS信號抗干擾能力強、截獲率低、保密性強等優點[23]的基礎上,軟擴頻技術提高了傳輸效率、占用的帶寬小,比DSSS技術更難被截獲[48]。現如今,軟擴頻技術已被廣泛應用于通信領域,如挪威新一代戰地通信網提出采用(256,8)和(32,7)的正交矩陣編碼,寬帶碼分多址(wideband code division multiple access, WCDMA)使用(64,6)的Walsh碼軟擴頻技術等[9]。因此,研究軟擴頻信號的偽碼序列盲估計具有重要意義。
關于擴頻信號的偽碼序列盲估計問題,當前的研究已經較為成熟,如矩陣分解法[1011]、最大似然法[1213]、神經網絡法[1415]、三階相關函數[16](triple correlation function, TCF)等。但是,由于軟擴頻信號結合了編碼技術,上述算法對于軟擴頻信號大多不適用。同時,在非合作通信中,要想估計出軟擴頻信號的偽碼序列還需要估計進制數。現有針對軟擴頻信號偽碼序列盲估計的文獻還較少。文獻[17]利用傳統K-means聚類估計軟擴頻信號的偽碼序列。文獻[4]在此基礎上利用相似度最小準則選取初始聚類中心,在性能上有所提升。但是,該方法需要通過遍歷確定進制數,計算量較大。文獻[18]將改進的近鄰傳播算法引入到軟擴頻信號的偽碼序列估計中,該方法可以自動確定進制數,但是估計效果不太理想。文獻[9]提出自適應確定截斷距離的方法,結合密度峰聚類對軟擴頻信號偽碼序列進行估計,不再需要人為確定截斷距離。
在實際通信中,接收端在對信號下變頻解調時,由于載波估計會存在誤差并且下變頻后的有用信號需要避開低頻噪聲的影響,下變頻后的擴頻信號會帶有殘余頻偏[19]。而針對帶殘余頻偏的擴頻信號的研究主要集中于DSSS[2021]、周期長碼DSSS[22]、長短碼DSSS[23]等。文獻[20]基于子空間理論實現帶殘余頻偏的正交相移鍵控(quadrature phase shift keying, QPSK)-DSSS信號的偽碼序列估計,但是沒有考慮失步等情況。文獻[21]在此基礎上提出矩陣譜范數和矩陣特征值分解結合全數字鎖相環(digital phase locked loop, DPLL)的方法,不僅考慮失步的情況,還提高了算法的性能。文獻[22]利用特征分解和模糊酉矩陣估計帶殘余頻偏的周期長碼直擴信號的偽碼序列,并且使用DPLL消除殘余頻偏。文獻[23]提出一種特征值分解、DPLL和梅西算法相結合的方法解決文獻[22]不能直接估計帶殘余頻偏的周期長短碼信號的長碼和短碼的問題。目前,還沒有針對帶殘余頻偏的軟擴頻信號偽碼序列盲估計的研究。
針對上述問題,本文提出一種快速奇異值分解(singular value decomposition, SVD)結合DPLL的方法盲估計帶殘余頻偏的軟擴頻信號偽碼序列。該方法將待處理的信號進行采樣后不重疊分段,得到數據矩陣,每段長度為一倍偽碼周期,利用其自相關矩陣的右上角元素完成失步點估計。然后,利用估計到的失步點進行同步以后,重新分段組成數據矩陣,再根據自相關矩陣的較大特征值個數估計進制數。最后,利用多次快速SVD估計偽碼序列,利用DPLL消除殘余頻偏,完成帶殘余頻偏的軟擴頻信號的偽碼序列盲估計。
1 系統模型
軟擴頻信號的傳輸模型如圖1所示。
信息序列d(t)通過串/并轉換分成以k比特為一組,根據權值j=∑k-1l=0dl2l從M=2k條偽碼序列中選擇對應的偽碼序列進行擴頻[4]。其中,dl表示每組信息碼的第l個信息碼元,k為進制數,則基帶軟擴頻信號可以表示為
b(t)=∑+∞i=-∞cj(t-iT)(1)
式中:cj(t)=∑N-1n=0cj,ngc(t-nTc)為偽碼序列波形,N為偽碼序列碼元個數,cj,n=±1為第j條偽碼序列的第n個偽碼碼元,j=0,1,…,M-1,gc(t)為矩形脈沖函數;Tc、Tb、T=kTb=NTc分別表示偽碼碼元周期、信息碼元周期、偽碼周期。
信號b(t)經過上變頻以后送入信道,載波頻率為fc。信號在接收端經過正交下變頻后可以表示為
y(t)=
b(t-Tx)exp[j(2πfΔt-2πfΔTx+)]+n(t)(2)
式中:Tx(0≤Txlt;T)表示接收信號的隨機起始時間;殘余頻偏fΔ=f0-fc,f0為本振頻率,一般有f0≠fc,且f0fΔ;表示隨機初始相位;n(t)=nr(t)+jni(t)是方差為σ2n的復高斯白噪聲。
假設T和Tc已經通過估計得到,以Tc為采樣周期,對y(t)進行采樣,并按一倍偽碼周期T進行分段,得到數據矩陣X(τ)=[xτ1,xτ2,…,xτNd],Nd表示樣本數目,τ表示延時時間,τ∈[0,N-1]。其中,第i段數據表示為
xτi=Zτibτi+nτi(3)
式中:
bτi=[ci1,τ+1,ci1,τ+2,…,ci1,NN-τ位,ci2,1,ci2,2,…,ci2,ττ位]T
Zτi=diag[zτ(1),zτ(2),…,zτ(N)]
式中:ci1,m,ci2,m=±1,m=1,2,…,N分別表示選用的第i1條和i2條偽碼序列的第m位碼元;zτ(m)=exp{j[2πf1(iN-N+m-τ)+]},f1=fΔ·Tc表示歸一化殘余頻偏。
2 失步點和進制數估計
2.1 失步點估計
軟擴頻信號采用多條偽碼序列進行擴頻,不能用常規方法(如最大化Frobenius范數)估計失步點。因此,本文利用自相關矩陣元素進行失步點估計。
首先,對X(τ)計算自相關矩陣:
R(τ)=E[X(τ)X(τ)H](4)
在實際中,R(τ)可根據下式進行估計。當Nd→∞時,R^(τ)→R(τ)。IN為N×N階的單位矩陣。
R^(τ)=1NdX(τ)X(τ)H=1Nd∑Ndm=1xτm(xτm)H=
1Nd∑Ndm=1Zτmbτm(bτm)H(Zτm)H+σ2nIN(5)
其次,對R(τ)中每個元素取模得到矩陣R′(τ),減少殘余頻偏帶來的相位影響。將R′(τ)中的右上角元素(不包括對角線元素)取出并進行降序排序。將前〈N(2N-1)/6〉個元素的平方和記為r1(τ),〈·〉表示取最近整數,將剩余元素的平方和記為r2(τ)。
由文獻[17]可知,在漸進意義上,當接收信號不同步時,任意一列與其他列不一定相等且不一定正交,這會導致r1(τ)變小以及r2(τ)變大。因此,根據r1(τ)-r2(τ)取得最大值時的位置可以估計失步點:
τ^=N-argmaxτ∈[0,N-1][r1(τ)-r2(τ)](6)
2.2 進制數估計
按第2.1節估計的失步點對采樣信號以T為采樣周期重新分段:X=[x1,x2,…,xNd]。第i段數據表示為
xi=Zibi+ni(7)
Zi=diag[z(1),z(2),…,z(N)](8)
式中:z(m)=exp{j[2πf1(iN-N+m)+]};Z=[Z1,Z2,…,ZNd];bi表示第i組信息碼對應的偽碼序列。
假設M條偽碼序列相互正交,則
BBH=[b1,b2,…,bNd][b1,b2,…,bNd]H=
∑Ndm=1bmbHm=∑Mi=1licicHi(9)
式中:B表示基帶軟擴頻信號矩陣,B=[b1,b2,…,bNd];li表示Nd組信息碼元中第i條偽碼序列被選用了li次。
對BBH進行特征分解可得BBH=VDVH,其中V為酉矩陣,D為對角矩陣。而X的自相關矩陣為
RX=1NdXXH=(Z1V)D(Z1V)H+σ2nIN(10)
由式(9)可知,BBH的主分量特征向量為偽碼序列集合,且存在M個較大特征值。由式(10)可知,RX雖然會受到殘余頻偏的影響,但是依然存在M個較大特征值。因此,可以根據這一性質估計進制數。
首先將RX的特征值降序排序,記為d1=[λ1,λ2,…,λN],(λ1≥λ2≥…≥λN)。其次,令d2=[λ′1,λ′2,…,λ′N-1],其中λ′i=λi-λi+1,i=1,2,…,N-1。一般Mlt;N/2,則可以估計出進制數M^:
M^=maxid2(i)gt;1.5〈N/2〉∑〈N/2〉m=1d2(m),
i=1,2,…,N-1(11)
3 偽碼序列估計
3.1 多次SVD估計偽碼序列
從理論上講,根據式(9)和式(10)可求得帶殘余頻偏的偽碼序列集合。但在實際過程中,由于偽碼序列的不完全正交、噪聲等因素的影響,當k≥2時,將直接提取主分量特征向量再消除殘余頻偏后的序列作為偽碼序列估計值的誤差會很大。
在此基礎上,本文首先進行奇異值逆過程降噪[24],然后通過多次SVD逐一細分數據,盡可能保證每個集合對應一種偽碼序列,再提取主分量特征向量,加入待處理的偽碼序列集合,達到提高正確率的效果。
令X′=XT,則
X′X′H=(XHX)T=
xT1x*1…xT1x*j…xT1x*Nd
xTjx*1…xTjx*j…xTjx*Nd
xTNdx*1…xTNdx*j…xTNdx*Nd(12)
式中:(·)*表示共軛,且
xTix*j=bTiZTiZ*jb*j+nTin*j=
exp[j2πf1N(i-j)]bTib*j+nTin*j(13)
當i=j時,xTix*j2=c2+ni2;當i≠j時,若bi=bj,xTix*j2=c2,否則xTix*j2=0。因此,X′X′H可作為相似性矩陣。
對X′X′H每個元素取模以后進行SVD:R1=U1D1VH1。U1前M列列向量表征與M條偽碼序列的相關性,該值越大,相關性越大[25]。
根據U1的前M列的取值將Nd組樣本對象劃分為M個集合,每個樣本對象歸到U1中對應列中元素模最大的集合中。將這M個集合記為X1~XM,其中每一行代表一個樣本對象。此時,每個集合包含的樣本對象大部分同屬于一條偽碼序列。
對X1進行SVD:X1=U2D2VH2。U2的列向量為X1XH1的特征向量,V2的列向量為XH1X1的特征向量。
根據U2前兩列的取值將X1中的樣本對象劃分為2個集合,取V2第一列向量構成新的向量c-1,作為第一條偽碼序列的估計值。
對其他M-1個集合重復上述操作,依次獲得M條偽碼序列的粗估計值,記為C-=[c-1,c-2,…,c-M]。這樣進行兩次SVD,即可以進一步減少其他偽碼序列帶來的影響。
為了進一步逼近真實偽碼序列取值,本文通過相似度準則重新對所有樣本對象進行劃分,將樣本對象劃分到具有最大相似度的集合中。其中,第i個樣本對象和第j條偽碼序列估計值的相似度為
S(i,j)=xTic-Hj(14)
然后,將每個集合表示成矩陣形式,在進行SVD以后獲得右奇異矩陣,取第一列向量作為偽碼序列估計值c′i(i=1,2,…,M),其中每一行表示一個樣本對象。最終得到M條偽碼序列的精確估計值,記為C′=[c′1,c′2,…,c′M]。
3.2 快速SVD算法
由于多次SVD會消耗過多的計算時間,即使是精確截斷的SVD,因此本文使用塊克雷洛夫近似SVD算法代替SVD算法,在保證精度損失較少的前提下加快計算速度[26]。為盡可能加快速度,選擇超采樣參數s=0,冪迭代參數P=1,算法簡化后的具體步驟如下。
對于秩為k的矩陣Am×n,首先生成一個標準正態分布的隨機矩陣Ωn×k,利用正交三角分解求在ΑΩ張成空間的一組正交向量H1:
[H1,~]=qr(AΩ,0)(15)
參數0表示只求解前k個列向量。
其次,對H1再求QR分解:
[Q,~]=qr(H1,0)(16)
令B=QHA,對其進行SVD,得到:
B=UbDbVHb(17)
令Ub=QUb,然后分別取Ub、Db、Vb的前k列:Ub=Ub(:,1:k),Db=Db(:,1:k),Vb=Vb(:,1:k)。
此時,可以得到矩陣A的近似SVD:A≈UbDbVHb。
3.3 DPLL消除殘余頻偏
令最終要得到的偽碼序列集合估計值為C~=[c~1,c~2,…,c~M],而第3.1節得到的偽碼序列還帶有殘余頻偏:C′=Z1C~=[c′1,c′2,…,c′M],其中c′i的第l(l=1,2,…,N)個元素為
c′i(l)=c~i(l)exp[j(2πf1l+)](18)
因此,接下來需要利用DPLL消除殘余頻偏。DPLL由鑒相器(phase detector, PD)、環路濾波器(loop filter, LF)和壓控振蕩器(voltage controlled oscillator, VCO)三部分組成[22],結構如圖2所示。
其中,PD采用反正切PD,用于計算相位差Δ;Δ經過LF后用于控制VCO的瞬時輸出相位′(l),LF的兩個參數KP和KI通過搜索最佳的幅頻和相頻特性選擇[27]。
取c′i(l)的實部和虛部:
c′i,I(l)=c~i(l)cos(2πf1l+)
c′i,Q(l)=c~i(l)sin(2πf1l+)(19)
對式(19)進行相位旋轉:
c~i,I(l)=c′i,I(l)cos[′(l)]+c′i,Q(l)sin[′(l)]
c~i,Q(l)=c′i,Q(l)cos[′(l)]-c′i,I(l)sin[′(l)](20)
將式(19)代入式(20),有
c~i,I(l)=c~i(l)cos(Δ)
c~i,Q(l)=c~i(l)sin(Δ)(21)
式中:Δ=(2πf1l+)-′(l)。當DPLL穩定工作時,DPLL的跟蹤相位′(l)→2πf1l+,即Δ→0,由式(21)可得
c~i,I(l)=c~i(l)
c~i,Q(l)=0(22)
由此可得到消除殘余頻偏的偽碼序列估計值。
總結以上內容,本文所提方法的具體步驟如下:
步驟 1 對待處理信號y(t)進行采樣后按一倍偽碼周期分段,得到數據矩陣X(τ),再根據式(6)估計失步點,得到同步后的數據矩陣X。
步驟 2 根據式(11)估計進制數M^。
步驟 3 對X進行SVD,保留前M^個奇異值,將剩余置零,然后利用奇異值逆過程降噪:X~=(USM^VT+X)/2。
步驟 4 初始化循環次數t=0,令X′=X~T。
步驟 5 對X′X′H的每個元素取模以后進行快速SVD,根據左奇異矩陣的前M^列的取值將Nd組樣本對象劃分為M^個集合,記為X1~XM。
步驟 6 對X1~XM分別進行快速SVD,再根據左奇異矩陣前兩列的取值將集合中的樣本對象劃分為2個集合,取右奇異矩陣第一列向量構成新的向量c-t+1,將其作為第t+1條偽碼序列粗估計值,并更新矩陣C-=[C-,c-t+1]。
步驟 7 利用式(14)重新將樣本對象劃分為M^個集合,對每個集合寫成矩陣形式后進行SVD,取右奇異矩陣的第一列向量作為偽碼序列估計值,記為C′=[c′1,c′2,…,c′M]。
步驟 8 利用DPLL消除C′的殘余頻偏,得到最終的偽碼序列估計值C~=[c~1,c~2,…,c~M]。
3.4 算法復雜度分析
本文步驟1估計失步點的算法計算復雜度為O(N2c);步驟2估計M需要進行一次特征值分解,算法計算復雜度為O(N3d);步驟3進行一次SVD,算法計算復雜度為O(N3d);本文在使用快速SVD算法時取P=1、k=M,算法計算復雜度為O(M+M2Nd),偽碼序列估計需要M+2次快速SVD,其中M次快速SVD中k=2,則算法計算復雜度為O(M+MNd+M2Nd)。
因此,本文估計偽碼序列時總的算法計算復雜度為O(N2c+N3d+M+MNd+M2Nd)。而傳統特征值分解法、SVD的算法計算復雜度分別為O(N3c+NdN2c)、O(N2c+N2dNc+N3d)。由此可知,本文參數估計的時間復雜度與M無關,主要耗時部分在于偽碼序列的估計。當M較小時,本文算法計算復雜度與這兩種算法相差不大;當M較大時,本文算法計算復雜度會更大。
4 仿真實驗及分析
本節進行仿真實驗,在每個信噪比(signal to noise ratio,SNR)下,分別進行300次蒙特卡羅仿真實驗。
實驗 1 驗證本文方法失步點估計的有效性
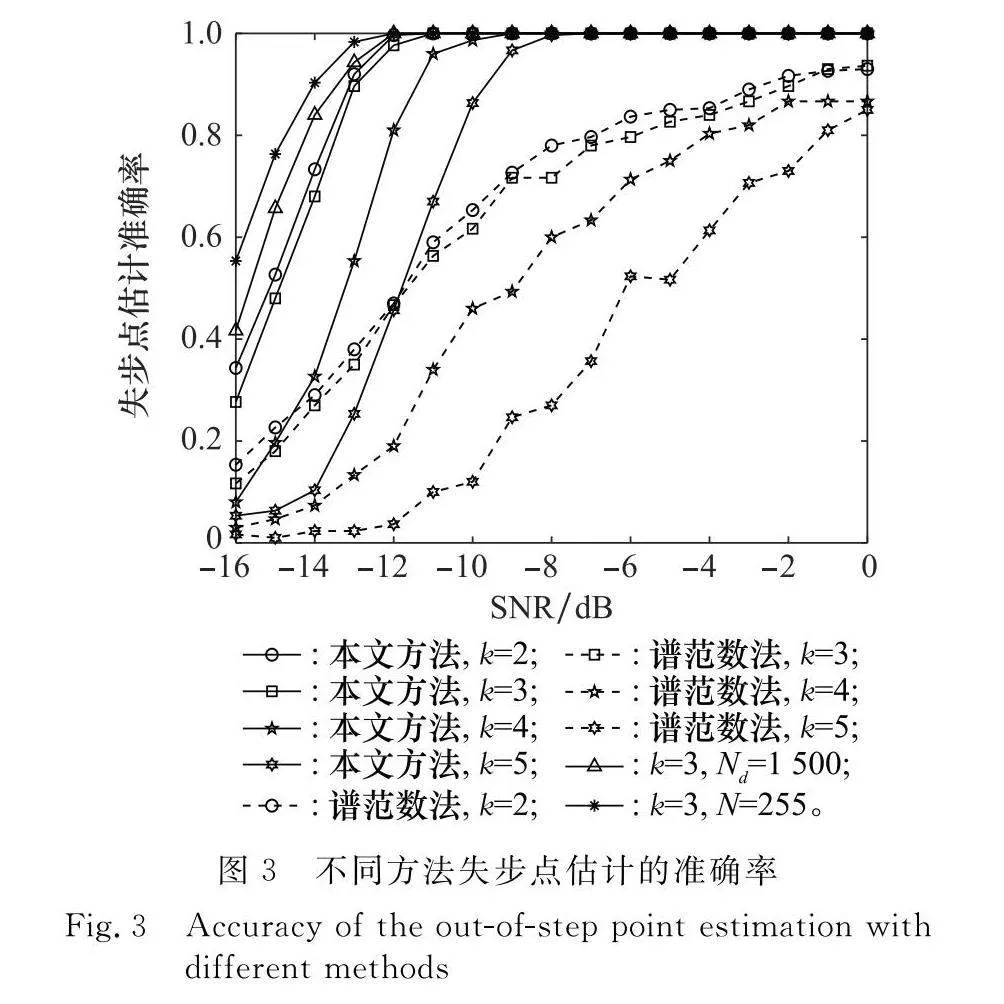
設信號采樣周期為Ts=Tc,歸一化殘余頻偏為f1=0.02,隨機起始點為Tx=23Tc,SNR取-16~0 dB。偽碼序列為gold序列,N分別取127 bit、255 bit,k分別取2、3、4、5,樣本數目Nd分別取1 000、1 500。將本文方法與譜范數法作對比實驗,結果如圖3所示。
由圖3可知,本文方法比譜范數法失步點估計效果好,可以保證在SNR≥-8 dB、k≤5時實現準確率為1的估計。其次,k越大,失步點估計的準確率越低,這是由于相同偽碼長度的情況下,k越大,即進制數越大,不同偽碼序列之間的相似度會越高,導致起始點移動以后的差異不明顯,估計準確率隨之增大。另外,偽碼長度的增加和樣本數目的增加都可以減小噪聲方差的影響,所以估計準確率會相應提高。
實驗 2 驗證本文方法進制數估計的有效性
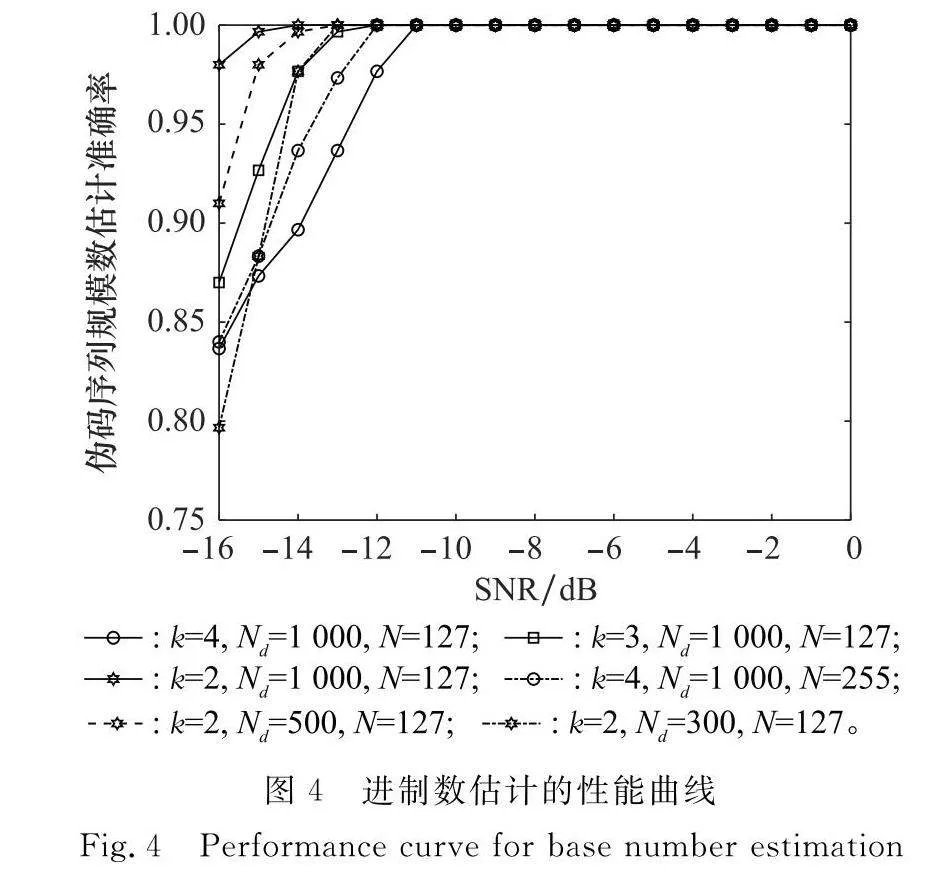
設信號采樣周期Ts=Tc,歸一化殘余頻偏為f1=0.02,SNR取-16~0 dB。偽碼序列為gold序列,N分別取127 bit、255 bit,k分別取2、3、4,Nd分別取1 000、500、300。仿真實驗結果如圖4所示。
由圖4可知,本文方法可以保證在SNR≥-10 dB、k≤4時估計準確率為1。另外,k越大,估計的準確率越低,這是因為總的樣本數目不變但是隨著k增大,會造成同一集合的樣本數目相對減少,因此估計的準確率會下降。而偽碼長度的增加和樣本數目的增加都可以提高估計的準確率。
實驗 3 驗證本文方法偽碼序列估計的有效性
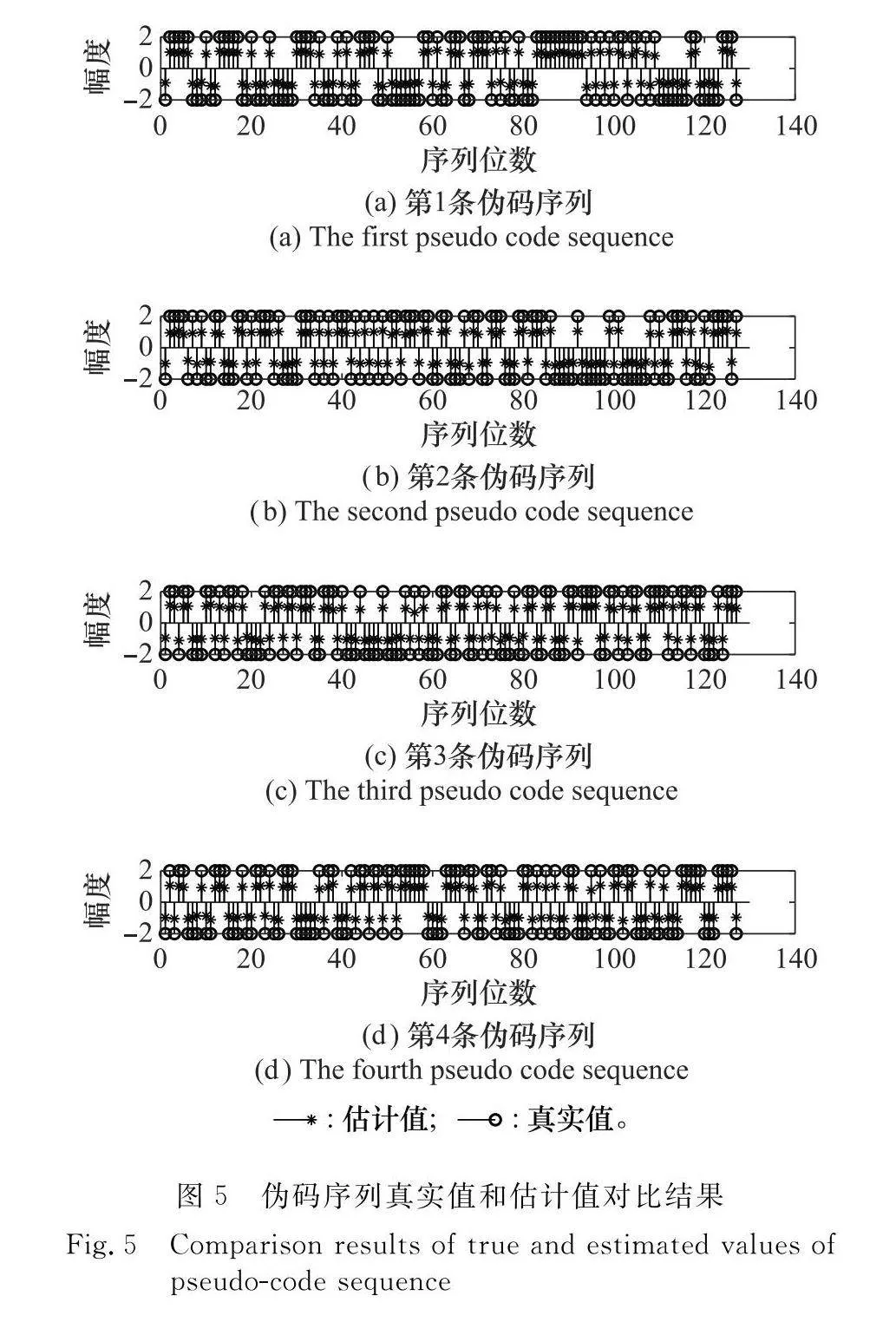
設信號采樣周期為Ts=Tc,歸一化殘余頻偏為f1=0.02,隨機起始點為Tx=23Tc,SNR取-5 dB。偽碼序列為gold序列,取N=127 bit,k=2,樣本數目Nd=1 000,進行仿真實驗,結果如圖5所示,為使對比效果更明顯,這里將真實值放大到2倍。
由圖5可知,本文方法可以成功估計出偽碼序列,證實了本文方法的有效性。
實驗 4 比較不同情況下本文方法估計帶殘余頻偏的軟擴頻信號的偽碼序列的性能
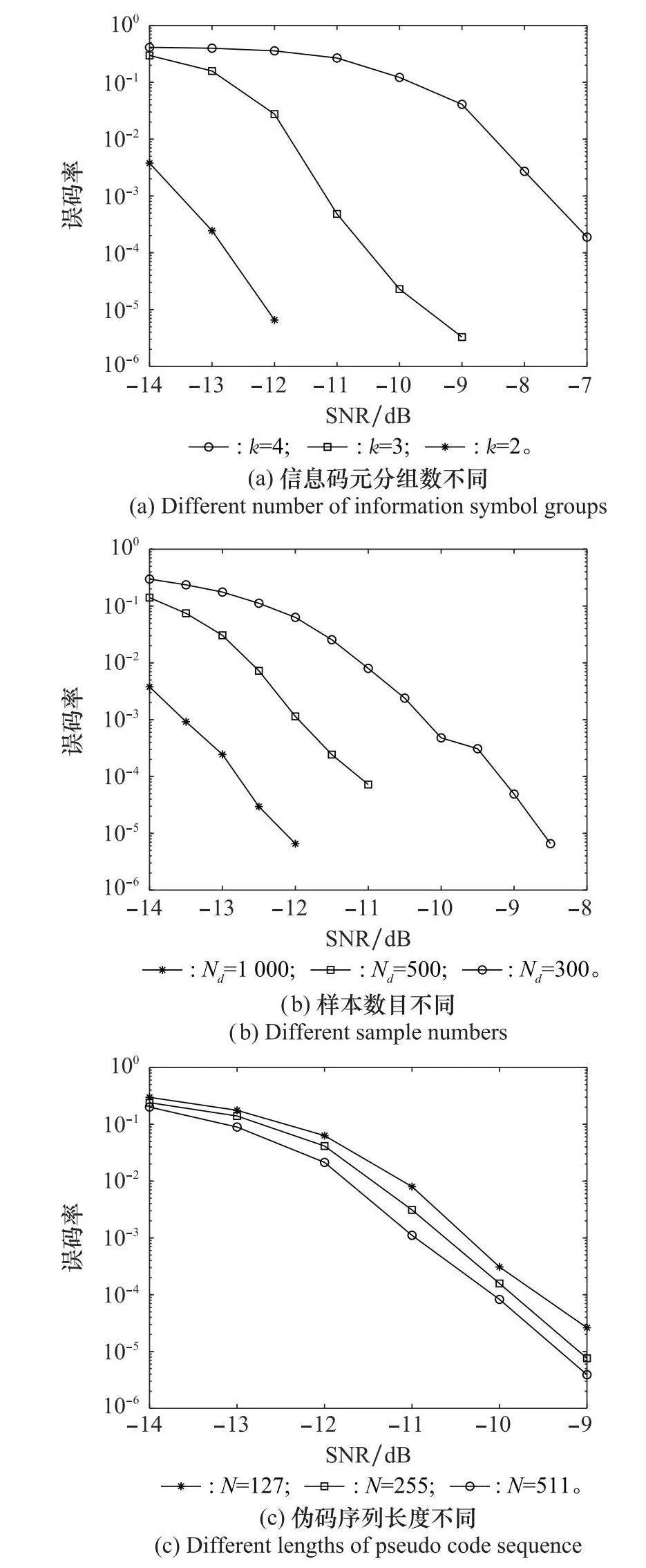
設信號采樣周期Ts=Tc,歸一化殘余頻偏f1=0.02,SNR取-14~0 dB。選取不同情況進行對比實驗,結果如圖6所示,其中具體參數如下。
圖6(a):碼型為gold序列;N=127 bit;Nd=1 000;k分別取2、3、4。
圖6(b):碼型為gold序列;N=127 bit;Nd分別取1 000、500、300;k=2。
圖6(c):碼型為gold序列;N分別取127 bit、255 bit、511 bit;Nd=300;k=2。
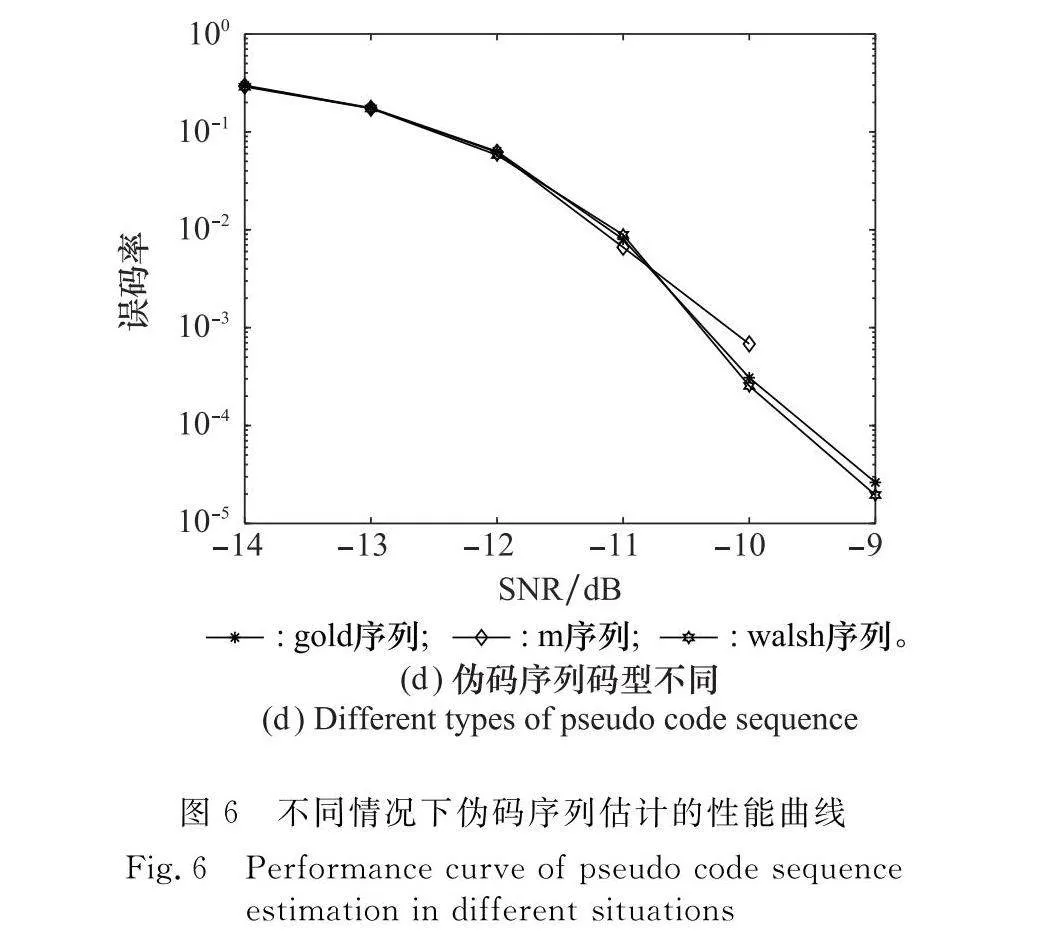
圖6(d):碼型分別為m序列、gold序列、walsh碼序列;N=127 bit;Nd=300;k=2。
由圖6可知,在其他條件不變時,增加SNR可以有效提高估計的準確性。其次,不同碼型下偽碼序列估計的誤碼率幾乎相同,因此本文方法對偽碼序列碼型不敏感。另外,k的增大、偽碼長度的減小和樣本數目的減小都會增大誤碼率。這是因為這3種情況都會增大不同偽碼序列之間的相互干擾以及放大噪聲帶來的影響,導致誤碼率隨之增大。
實驗 5 分析殘余頻偏對偽碼序列估計的影響
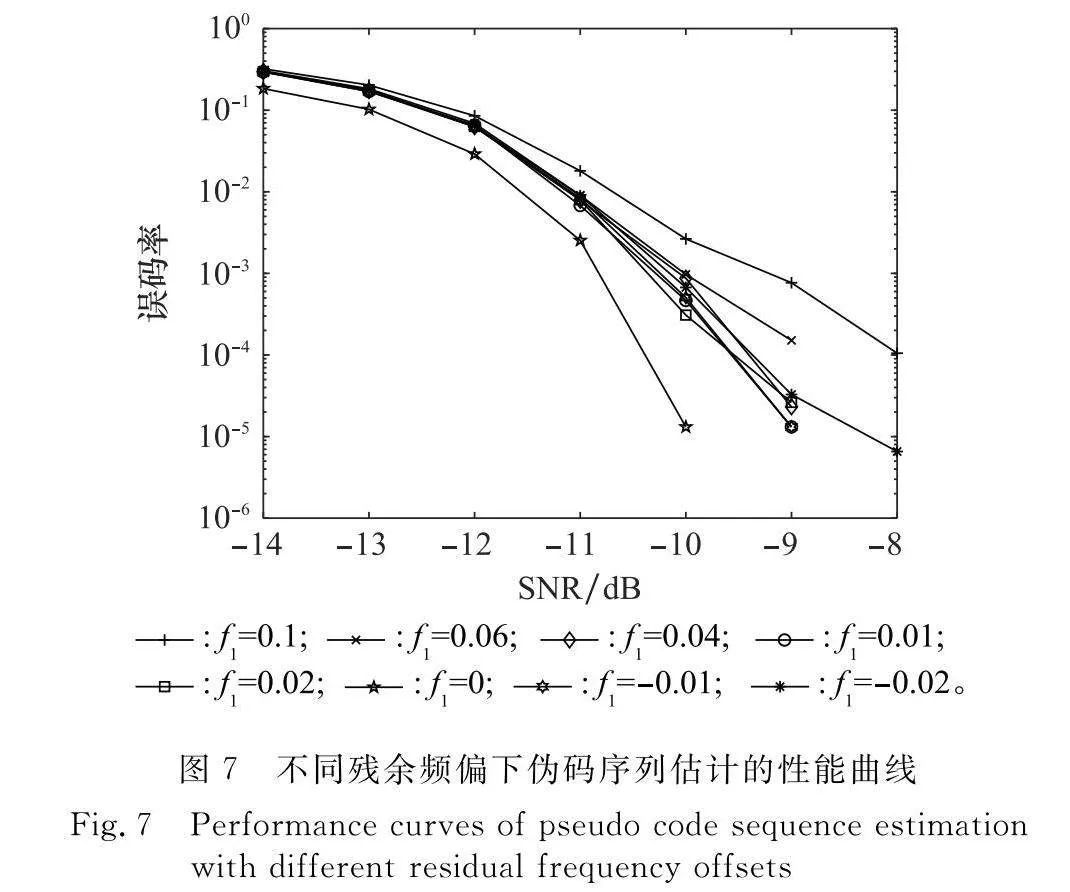
設信號采樣周期Ts=Tc,SNR取-14~0 dB,偽碼序列為gold序列,長度N=127 bit,信息碼元按k=2分為一組,樣本數目Nd=300。歸一化殘余頻偏f1分別取0.1、0.06、0.04、0.02、0.01、0、-0.01、f1=-0.02進行仿真實驗,結果如圖7所示。
由圖7可知,在不同情況下,誤碼率均隨著SNR的提高而減小。在相同SNR下,有殘余頻偏比無殘余頻偏的估計誤碼率大,并且隨著殘余頻偏的增大,估計性能有所下降,但是下降幅度較小。因此,本文用DPLL消除殘余頻偏具有一定穩定性。
實驗 6 對比實驗
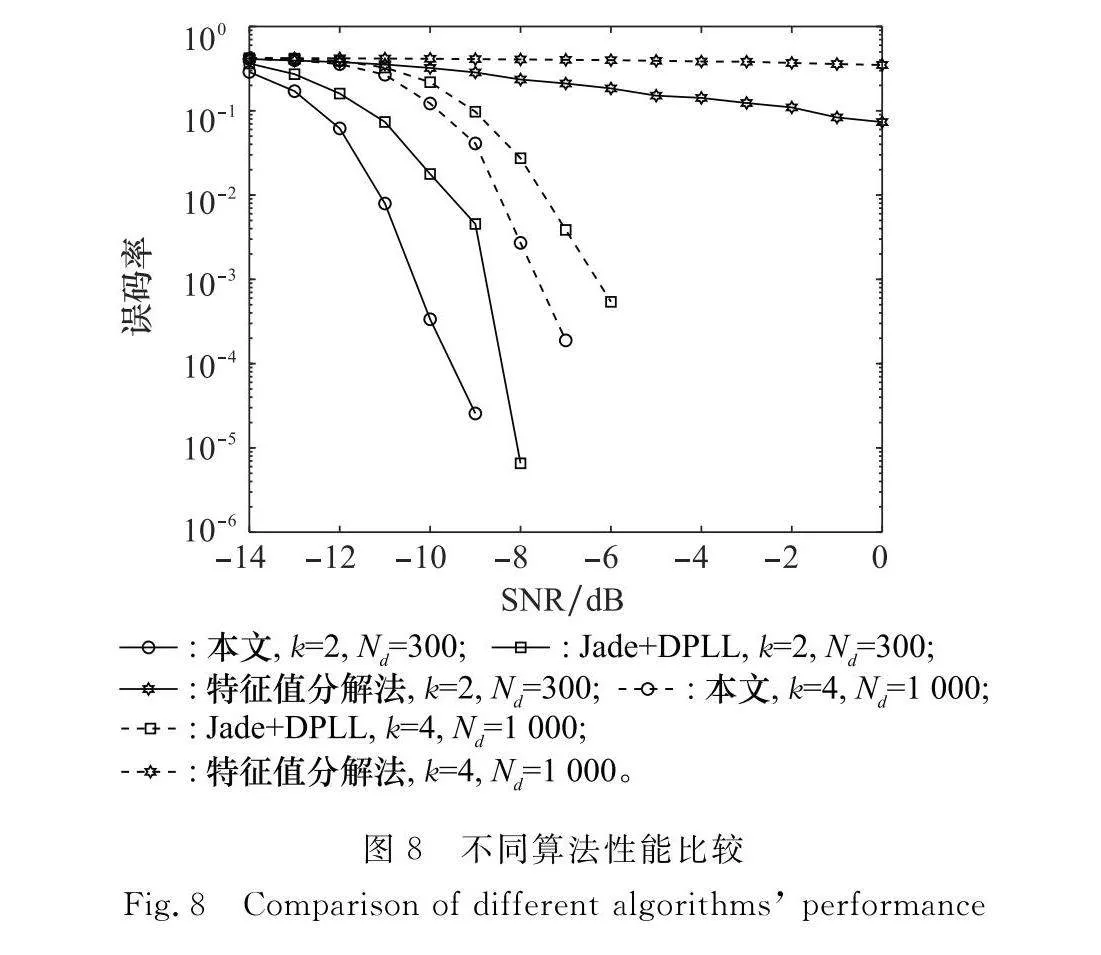
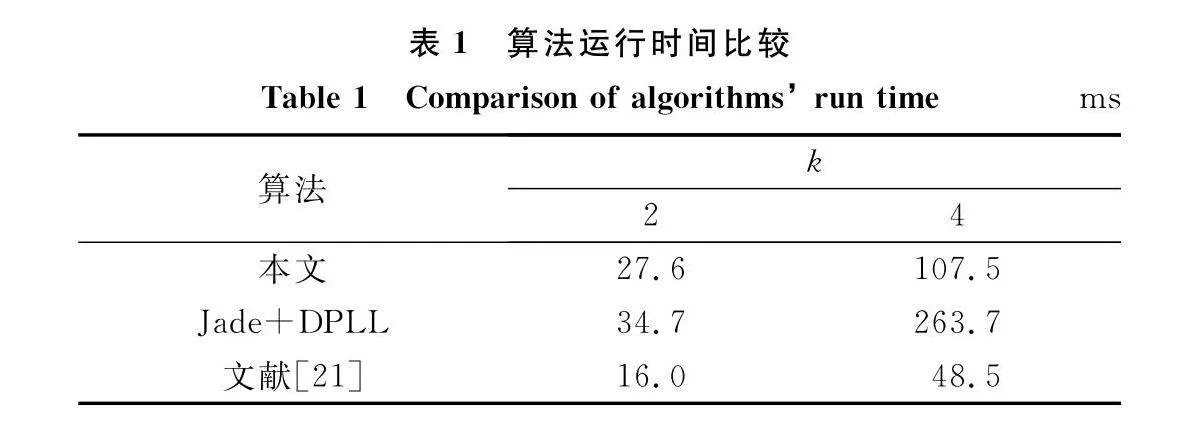
設信號采樣周期為Ts=Tc,SNR取-14~0 dB,偽碼序列為gold序列,取N=127 bit,k分別取2、4,歸一化殘余頻偏取f1=0.02,樣本數目Nd分別取300、1 000。分別用本文方法、Jade加DPLL算法、特征分解方法[21]進行
仿真實驗,誤碼率如圖8所示,SNR為-14~0 dB的平均運行時間如表1所示。
由圖8和表1可知,文獻[21]所提算法雖然運行時間最短,但是誤碼率最高,而本文算法雖然需要更多的運行時間,但是性能明顯優于其他算法。因此,本文算法是犧牲了一定時間換取準確度的提升。
5 結 論
針對帶殘余頻偏的軟擴頻信號偽碼序列盲估計問題,本文提出一種快速SVD結合DPLL的方法。首先,對待處理信號分段生成數據矩陣,然后,根據其自相關矩陣的右上角元素完成失步點的估計;其次,在同步基礎上,根據信號自相關矩陣特征值較大個數估計進制數;最后,使用多次快速SVD對偽碼序列進行估計,以DPLL消除殘余頻偏,恢復出原始偽碼序列。仿真結果證明了本文方法的有效性,在SNR=-11 dB、樣本數目為300、k=2的條件下,偽碼序列估計的誤碼率可以達到0.1以下。與其他方法相比,本文方法性能明顯優于其他算法。
參考文獻
[1] PURSLEY M B, ROYSTER T C. High-rate direct-sequence spread spectrum with error control coding[J]. IEEE Trans.on Communications, 2006, 54(9): 16931702.
[2] XU L, LIU X X, ZHANG Y J. Blind estimation of spreading code sequence of QPSK-DSSS signal based on fast-ICA[J]. Information, 2023, 14(2): 112.
[3] REN J F, XU K, LIU Y, et al. DSSS signal jamming method based on DCGAN[C]∥Proc.of the 6th International Conference on Information Communication and Signal Processing, 2023: 285289.
[4] 張天騏, 楊強, 宋玉龍, 等. 一種K-means改進算法的軟擴頻信號偽碼序列盲估計[J]. 電子與信息學報, 2018, 40(1): 226234.
ZHANG T Q, YANG Q, SONG Y L, et al. Blind estimation PN sequence in soft spread spectrum signal of improved K-means algorithm[J]. Journal of Electronics amp; Information Technology, 2018, 40(1): 226234.
[5] YANG G, ZHOU F, LOU Y, et al. Double-differential coded M-ary direct sequence spread spectrum for mobile underwater acoustic communication system[J]. Applied Acoustics, 202 183: 108303.
[6] RA H, YOUN C, KIM K. High-reliability underwater acoustic communication using an M-ary cyclic spread spectrum[J]. Electronics, 2022: 11(11): 1698.
[7] ANJANEYA M V D B, CHINTHALA S, BASIRI M M A. Flexible circuit designs of M-ary digital modulations and demodulations[C]∥Proc.of the 3rd International Conference on Electrical, Computer, Communications and Mechatronics Engineering, 2023.
[8] LIU R P, WANG P Y, WANG X D. Application of soft-decision decoding algorithm for convolution coding of M-ary spread spectrum signals[C]∥Proc.of the 5th International Conference on Intelligent Control, Measurement and Signal Processing, 2023: 10031010.
[9] 張丹娜, 楊曉靜, 馮輝, 等. 改進Walsh碼軟擴頻盲解擴算法[J]. 系統工程與電子技術, 2019, 41(10): 23782384.
ZHANG D N, YANG X J, FENG H, et al. Improved Walsh code soft spread spectrum blind despreading algorithm[J]. Systems Engineering and Electronics, 2019, 41(10): 23782384.
[10] QIANG X Z, ZHANG T Q. Estimation of spreading code in non-periodic long-code DSSS signal[C]∥Proc.of the 6th International Conference on Wireless Communications, Signal Processing and Networking, 2021: 162165.
[11] WU L P, LI Z, LI J D, et al. A PN sequence estimation algorithm for DS signal based on average cross-correlation and eigenanalysis in lower SNR conditions[J]. Science China Information Sciences, 2010, 53(8): 16661675.
[12] CHOI Y, KIM D, JANG M, et al. Spreading sequence blind estimation in DSSS system using gradient ascent method[C]∥Proc.of the 33rd International Telecommunication Networks and Applications Conference, 2023: 7679.
[13] CHOI H, MOON M. Blind estimation of spreading sequence and data bits in direct-sequence spread spectrum communication systems[J]. IEEE Access, 2020, 8: 148066148074.
[14] WEI Y J, FANG S L, WANG X Y, et al. Blind estimation of the PN sequence of a DSSS signal using a modified online unsupervised learning machine[J]. Sensors, 2019, 19(2): 354.
[15] CHENG H, LUO Z H, SUN G. Non-supervised rule for direct sequence spread spectrum signal sequence acquisition[C]∥Proc.of the 9th International Conference on Broadband amp; Wireless Computing, 2015: 151154.
[16] GU X W, ZHAO Z J, SHEN L. Blind estimation of pseudo-random codes in periodic long code direct sequence spread spectrum signals[J]. IET Communications, 2016, 10(11): 12731281.
[17] LI J W, ZHANG T Q, YANG C S, et al. Clustering based blind estimation of PN sequences in M-ary spread spectrum system[C]∥Proc.of the International Conference on Mechatronic Sciences, Electric Engineering and Computer, 2014: 866869.
[18] 李丞, 張玉. 基于改進近鄰傳播算法的Walsh軟擴頻盲解擴方法[J]. 火力與指揮控制, 2019, 44(3): 7781.
LI C, ZHANG Y. Blind despread method of Walsh soft spread spectrum based on improved affinity propagation algorithm[J]. Fire Control amp; Command Control, 2019, 44(3): 7781.
[19] YANG R, ZHANG T Q, WU W J, et al. Blind estimation for the period of pseudo noise code and the combination code in binary offset carrier signal[C]∥Proc.of the 7th International Congress on Image and Signal Processing, 2014: 10001005.
[20] QIU Z Y, PENG H, LI T Y. A blind despreading and demodulation method for QPSK-DSSS signal with unknown carrier offset based on matrix subspace analysis[J]. IEEE Access, 2019, 7: 125700125710.
[21] 陳顯露, 張天騏, 孟瑩, 等. 帶殘余頻偏的QPSK-DSSS信號偽碼序列盲估計[J]. 北京郵電大學學報, 202 45(3): 9095.
CHEN X L, ZHANG T Q, MENG Y, et al. Blind estimation of pseudo-code sequence of QPSK-DSSS signal with residual carrier[J]. Journal of Beijing University of Posts and Telecommunications, 202 45(3): 9095.
[22] 喻盛琪, 張天騏, 范聰聰, 等. 帶殘余載波的周期長碼直擴信號PN碼盲估計[J]. 信號處理, 2019, 35(10): 16611670.
YU S Q, ZHANG T Q, FAN C C, et al. Blind estimation of PN codes for periodic long-code DSSS signals with residual carrier[J]. Journal of Signal Processing, 2019, 35(10): 16611670.
[23] 潘微宇, 趙知勁, 王李軍. 帶殘余載波的LSC-DSSS信號偽隨機碼盲估計[J]. 火力與指揮控制, 202 47(7): 9710 107.
PAN W Y, ZHAO Z J, WANG L J. Pseudo random code blind estimation of LSC-DSSS signal with residual carrier[J]. Fire Control amp; Command Control, 202 47(7): 9710 107.
[24] 王麗敏, 姬強, 韓旭明, 等. 基于奇異值分解的自適應近鄰傳播聚類算法[J]. 吉林大學學報(理學版), 2014, 52(4): 753757.
WANG L M, JI Q, HAN X M, et al. Self-adaptive affinity propagation clustering algorithm based on singular value decomposition[J]. Journal of Jilin University(Science Edition), 2014, 52(4): 753757.
[25] 戴月明, 王明慧, 張明, 等. SVD優化初始簇中心的K-means中文文本聚類算法[J]. 系統仿真學報, 2018, 30(10): 38353842.
DAI Y M, WANG M H, ZHANG M, et al. Optimizing initial cluster centroids by SVD in K-means algorithm for Chinese text clustering[J]. Journal of System Simulation, 2018, 30(10): 38353842.
[26] HALKO N, MARTINSSON P G, SHKOLNISKY Y, et al. An algorithm for the principal component analysis of large data sets[J]. SIAM Journal on Scientific Computing, 201 33(5): 25802594.
[27] ZHANG T Q, DAI S S, MA G N, et al. Blind estimation of the PN sequence in lower SNR DS-SS signals with residual carrier[J]. Digital Signal Processing, 201 22(1): 106113.
作者簡介
張天騏(1971—),男,教授,博士,主要研究方向為通信信號的調制解調與盲處理、語音信號處理、神經網絡實現、現場可編程門陣列、超大規模集成電路實現。
張慧芝(2000—),女,碩士研究生,主要研究方向為擴頻信號盲處理。
羅慶予(1999—),女,碩士研究生,主要研究方向為語音信號處理、語音增強。
方 蓉(1999—),女,碩士研究生,主要研究方向為衛星擴頻信號捕獲。

