機載高分辨CSSAR地面加速運動目標成像方法

摘 要：機載圓軌跡條帶合成孔徑雷達（circular stripmap synthetic aperture radar， CSSAR）的圓軌跡運動導致目標信號特性復雜、目標距離方程高階分量顯著等問題，給運動目標成像帶來很多困難。考慮到高分辨是未來的發展趨勢，針對機載高分辨CSSAR，提出一種地面加速運動目標成像方法。首先，針對目標距離方程高階分量顯著的問題，建立了四階Taylor近似距離模型，以保證成像質量。接著，推導了目標二維頻域信號模型，提出通過二維頻域相位相乘來高效地實現目標聚焦，并利用差分進化算法高效地實現對距離模型各參數的精確搜索。最后，通過實驗驗證了所提方法的有效性。

關鍵詞： 機載圓軌跡條帶合成孔徑雷達; 地面運動目標成像; 距離方程

中圖分類號： TN 951 文獻標志碼： A""" DOI：10.12305/j.issn.1001-506X.2024.10.12

Ground accelerating moving target imaging method for airborne

high-resolution CSSAR

LI Yongkang ZHU Jirong， YANG Chenxi

（School of Electronics and Information， Northwestern Polytechnical University， Xi’an 71007 China）

Abstract： The airborne circular stripmap synthetic aperture radar （CSSAR） has complex target signal characteristics and significant high-order components of the target range equation due to its circular motion， which brings many difficulties to the imaging of moving targets. Considering that high-resolution is the future development trend， a ground accelerated moving target imaging method is proposed for airborne high-resolution CSSAR. Firstly， to address the issue of significant high-order components in the target range equation， a fourth-order Taylor approximate range model is established to ensure the imaging quality. Next， a two-dimensional frequency-domain signal model of the target is derived， and it is proposed to efficiently achieve target focusing through two-dimensional frequency-domain phase multiplication. The differential evolution algorithm is also used to efficiently achieve accurate search of various parameters of the range model. Finally， the experimental results validate the effectiveness of the proposed method.

Keywords： airborne circular stripmap synthetic aperture radar （CSSAR）; ground moving target imaging; range equation

0 引 言

合成孔徑雷達（synthetic aperture radar， SAR）是一種強大的微波成像雷達，已在自然災害監測、海洋環境觀測、軍事偵察等領域發揮重要作用^［16］。SAR地面運動目標指示（ground moving target indication， GMTI）是SAR的一個重要應用。SAR-GMTI系統在獲取地面場景高分辨圖像的同時，能對其中的運動目標進行檢測、成像等，已在軍事情報收集、交通流量監測等領域得到應用^［713］。

近年來，在航空偵查與監視迫切需求的推動下，機載SAR發展迅速。其中，機載圓軌跡條帶SAR（circular stripmap SAR， CSSAR）就是在這種背景下發展起來的一種較新型的機載SAR^［1415］。其軌跡是一個圓，能多次觀測同一區域，且通過調整平臺速度以及運動半徑，可將重訪周期降低至數十秒。此外，由于雷達照射區域位于平臺軌跡的外側，機載CSSAR能夠獲得很大的觀測范圍。這兩個優點使得機載CSSAR適合執行GMTI任務，比如油庫、兵營、碼頭等重要區域的警戒^［16］。

在SAR-GMTI的一些應用場合，如航空偵察與監視，能夠對地面運動目標進行高質量的成像是非常有價值的，SAR地面運動目標成像因而成為近年來的一個研究熱點。對于機載CSSAR，人們已對地面靜止場景成像和地面勻速運動目標成像進行了較深入的研究^［1721］，但對于存在加速度的運動目標成像的研究還很不足。對于常規的直線軌跡SAR，國內外學者已經提出了較多的運動目標成像方法，且已能實現對加速目標的高質量成像^［2228］。但這些方法大多需要搜索或估計多個參數，因此存在計算量大的問題。例如，文獻［23］的方法利用Hough變換和相位相乘實現距離徙動校正，利用多項式傅里葉變換來實現方位壓縮。該方法需要兩次二維搜索，計算量較大。文獻［25］的方法則利用Hough變換和二階Keystone變換來分別校正目標的一次和二次距離徙動，利用三次相位函數隨機變換來估計目標相位歷程的二次項和三次項系數。該方法能實現對目標的高質量成像，但需要進行一次插值運算和兩次二維搜索，計算量較大。文獻［27］提出一種基于稀疏貝葉斯學習的成像方法，該方法成像質量很高，但由于要對6個參數進行搜索，計算量也較大。

與常規直線軌跡SAR不同，機載CSSAR的圓形運動軌跡導致目標距離方程的高階分量較顯著，從而增加了高效、高質量成像的難度。同時，高分辨是SAR的一個重要發展方向，高分辨也有利于獲得目標更詳細的信息，但高分辨系統的合成孔徑時間較長，此種情況下目標的加速度無法忽略，目標高效、高質量成像因此會面臨更多困難。

本文研究了機載高分辨CSSAR下加速運動目標的高效、高質量成像，并提出一種基于差分進化算法的成像方法。考慮到加速目標距離方程高階分量顯著，本文建立了四階Taylor近似距離模型，并推導了目標二維頻域信號模型。接著，通過二維頻域相位相乘高效地實現目標聚焦，并將目標成像建模成一個優化問題。最后，提出利用差分進化算法來高效求解上述優化問題。

1 信號建模

1.1 距離方程建模

圖1為機載CSSAR與地面運動目標之間的幾何關系。雷達平臺的運動軌跡為一個半徑為r_a的圓，雷達天線正側視且指向圓形軌跡的外側。假設目標做勻加速運動，且在方位慢時間t_a=0時，沿x軸、y軸的速度分別為v_x、v_y，加速度分別為a_x、a_y。假設在t_a=0時刻，雷達位于（r_a，0，h），目標位于（r₀，0，0），其中r₀為目標到坐標原點的初始距離，h為雷達高度。

根據圖1，目標的距離方程，即目標到雷達的瞬時距離，可表示為

R（t_a）=

（r₀+v_xt_a－r_acos（ωt_a））²+（v_yt_a－r_asin（ωt_a））²+h²（1）

式中：ω為雷達的角速度。

對式（1）在雷達波束中心穿越目標的時刻，即t_a=0時刻，進行4階Taylor展開，可得

R₄（t_a）≈R₀+l₁t_a+l₂t²_a+l₃t³_a+l₄t⁴_a（2）

式中：

R₀=（r₀－r_a）²+h²（3）

l₁=r₀－r_aR₀v_x=v_tr（4）

l₂=v²_x+（v_y－r_aω）²+（r₀－r_a）（a_x+ω²r_a）－v²_tr2R₀（5）

l₃=3（v_xa_x+v_xr_aω²+v_ya_y－r_aa_yω）6R₀－

3v_tr［v²_x+（v_y－r_aω）²+（r₀－r_a）（a_x+r_aω²）－v²_tr］6R²₀（6）

l₄=3（a²_x+a²_y）+6a_xr_aω²－ω⁴r_ar₀+4ω³r_av_y24R₀－

v_tr［v_x（a_x+ω²r_a）+a_y（v_y－ωr_a）］2R²₀－5v⁴_tr8R³₀－

［v²_x+（v_y－ωr_a）²+（r₀－r_a）（a_x+ω²r_a）］²8R³₀+

3v²_tr［v²_x+（r₀－r_a）（a_x+ω²r_a）+（v_y－ωr_a）²］4R³₀（7）

式中：R₀為t_a=0時刻目標與雷達之間的距離;v_tr為t_a=0時刻目標速度在雷達到目標徑向方向上的投影。

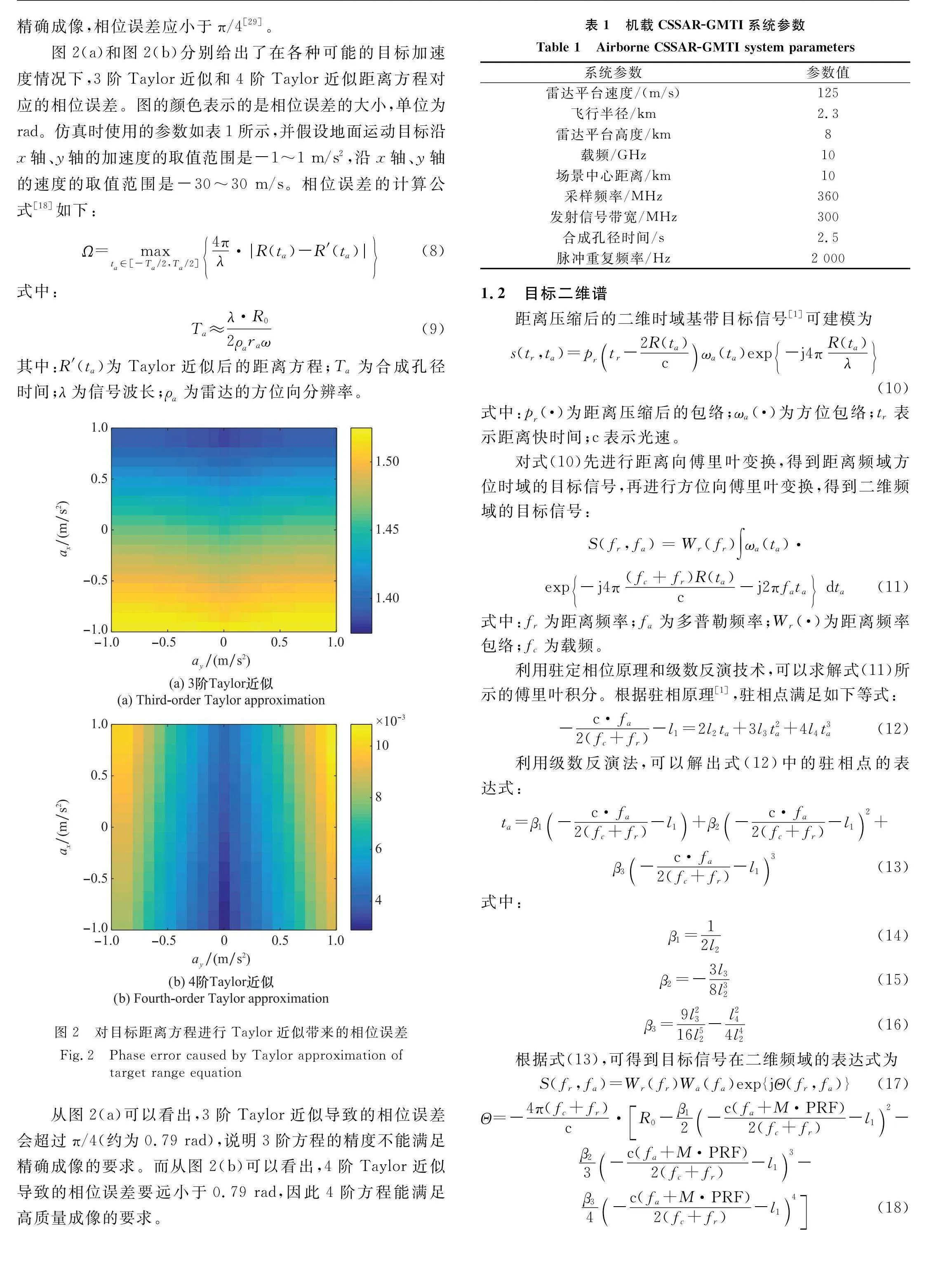
在對目標距離方程進行Taylor近似時，當系統分辨率較高或者目標存在加速度時，通常保留到3階項精度就足夠了。但對于機載CSSAR，雷達的圓跡運動導致目標距離歷程中的4階項也較顯著，因此本文保留到4次項。下面利用數值仿真，通過分析由Taylor近似導致的相位誤差，來論證保留到4階項的必要性。注意，為了實現對目標的精確成像，相位誤差應小于π/4^［29］。

圖2（a）和圖2（b）分別給出了在各種可能的目標加速度情況下，3階Taylor近似和4階Taylor近似距離方程對應的相位誤差。圖的顏色表示的是相位誤差的大小，單位為rad。仿真時使用的參數如表1所示，并假設地面運動目標沿x軸、y軸的加速度的取值范圍是-1～1 m/s²，沿x軸、y軸的速度的取值范圍是-30～30 m/s。相位誤差的計算公式^［18］如下：

Ω=maxta∈［－Ta/2，Ta/2］4πλ·|R（t_a）－R′（t_a）|（8）

式中：

T_a≈λ·R₀2ρ_ar_aω（9）

其中：R′（t_a）為Taylor近似后的距離方程;T_a為合成孔徑時間;λ為信號波長;ρ_a為雷達的方位向分辨率。

從圖2（a）可以看出，3階Taylor近似導致的相位誤差會超過π/4（約為0.79 rad），說明3階方程的精度不能滿足精確成像的要求。而從圖2（b）可以看出，4階Taylor近似導致的相位誤差要遠小于0.79 rad，因此4階方程能滿足高質量成像的要求。

1.2 目標二維譜

距離壓縮后的二維時域基帶目標信號^［1］可建模為

s（t_r，t_a）=p_rt_r－2R（t_a）cω_a（t_a）exp－j4πR（t_a）λ（10）

式中：p_r（·）為距離壓縮后的包絡;ω_a（·）為方位包絡;t_r表示距離快時間;c表示光速。

對式（10）先進行距離向傅里葉變換，得到距離頻域方位時域的目標信號，再進行方位向傅里葉變換，得到二維頻域的目標信號：

S（f_r，f_a）=W_r（f_r）∫ω_a（t_a）·

exp－j4π（f_c+f_r）R（t_a）c－j2πf_at_a dt_a（11）

式中：f_r為距離頻率;f_a為多普勒頻率;W_r（·）為距離頻率包絡;f_c為載頻。

利用駐定相位原理和級數反演技術，可以求解式（11）所示的傅里葉積分。根據駐相原理^［1］，駐相點滿足如下等式：

－c·f_a2（f_c+f_r）－l₁=2l₂t_a+3l₃t²_a+4l₄t³_a（12）

利用級數反演法，可以解出式（12）中的駐相點的表達式：

t_a=β₁－c·f_a2（f_c+f_r）－l₁+β₂－c·f_a2（f_c+f_r）－l₁2+

β₃－c·f_a2（f_c+f_r）－l₁3（13）

式中：

β₁=12l₂（14）

β₂=－3l₃8l³₂（15）

β₃=9l²₃16l⁵₂－l²₄4l⁴₂（16）

根據式（13），可得到目標信號在二維頻域的表達式為

S（f_r，f_a）=W_r（f_r）W_a（f_a）exp{jΘ（f_r，f_a）}（17）

Θ=－4π（f_c+f_r）c·

［R₀－β₁2－c（f_a+M·PRF）2（f_c+f_r）－l₁2－

β₂3－c（f_a+M·PRF）2（f_c+f_r）－l₁3－

β₃4－c（f_a+M·PRF）2（f_c+f_r）－l₁4］（18）

式中：W_a（·）為方位頻率包絡;M為目標的多普勒模糊數;PRF為脈沖重復頻率。注意，式（18）考慮了目標可能存在多普勒模糊，且f_a表示的是基帶多普勒頻率。

2 算法描述

本節將基于所推導的目標二維譜設計成像算法。首先，將成像過程建模為一個優化問題。接著，提出利用差分進化算法來高效地求解該優化問題。最后，將給出本文成像算法的處理流程。

2.1 將優化過程建模為優化問題

根據成像原理，只要補償二維頻域目標信號相位中的多普勒頻率和距離頻率的調制項（即二次及更高次項），就能實現對目標的聚焦。因此，構造如下濾波器：

H（f_r，f_a）=exp－j2π（f_c+f_r）β₁c·

［l²₁+c²（f2_a+M2·PRF²）4（f_c+f_r）²+c·M·PRF·l₁f_c+f_r］·

expj43π（f_c+f_r）β₂cc³（f3_a+3f2_aM·PRF+M3·PRF³）8（f_c+f_r）³+

3l₁c²（f2_a+M2·PRF²）4（f_c+f_r）²+l³₁+3l²₁c·M·PRF2（f_c+f_r）·

exp－jπ（f_c+f_r）β₃c·

c⁴（f⁴_a+4f3_aM·PRF+6f2_aM2·PRF²+M⁴·PRF⁴）16（f_c+f_r）⁴+

l₁c³（f3_a+3f2_aM·PRF+M3·PRF³）2（f_c+f_r）³+

3l²₁c²（f2_a+M2·PRF²）2（f_c+f_r）²+2l³₁cM·PRF（f_c+f_r）+l⁴₁（19）

將式（17）和式（19）相乘，再進行二維傅里葉逆變換，即可得到聚焦后的目標信號。需要注意的是，構造式（19）所示的濾波器，需要用到目標距離方程各次項系數l₁、l₂、l₃、l₄和多普勒模糊數M。但在實際中，這些參數都是未知的，因此在成像過程中需要進行參數搜索。當搜索到的值與其真實值一致時，目標會被準確聚焦，此時目標圖像的對比度會達到最大值。因此，成像過程可建模為以下優化問題：

（l^₁，l^₂，l^₃，l^₄）=

argmaxl1∈［l_1，min，l_1，max］，l2∈［l_2，min，l_2，max］

l3∈［l_3，min，l_3，max］，l4∈［l_4，min，l_4，max］{Contrast［s（t_r，t_a;l₁，l₂，l₃，l₄）］}（20）

式中：

Contrast［s（t_r，t_a;l₁，l₂，l₃，l₄）］=

E{［|s（t_r，t_a;l₁，l₂，l₃，l₄）|2－E（|s（t_r，t_a;l₁，l₂，l₃，l₄）|2）］²}E{|s（t_r，t_a;l₁，l₂，l₃，l₄）|2}（21）

s（t_r，t_a;l₁，l₂，l₃，l₄）=IDFT₂{S（f_r，f_a）·H（f_r，f_a）}（22）

式中：IDFT₂（·）表示二維傅里葉逆變換;E（·）表示空間平均操作;Contrast（·）為圖像對比度;l^₁、l^₂、l^₃、l^₄為參數的估計值；l_i，max和l_i，min分別為對應參數的最大值和最小值。目標的多普勒模糊數M可以根據l^₁求解出，其關系如下：

M^=round［2l^₁/（λ·PRF）］

其中：round［·］表示四舍五入運算。

從上面的分析可以看出，優化問題的解是4個參數的最優估計值。因此，聚焦SAR圖像如下：

I（t_r，t_a）=IDFT₂{S（f_r，f_a）·H（f_r，f_a;l^₁，l^₂，l^₃，l^₄）}（23）

如果使用文獻［22］的思路，采取遍歷搜索的方法解決上述優化問題，計算量會很大。為了提高效率，本文將利用差分進化算法求解該優化問題。

2.2 利用差分進化算法解決成像優化問題

差分進化算法是最強大的進化算法之一，包括4個基本步驟：初始化種群、變異、交叉或重組和選擇^［30］。首先將個體隨機地分布在種群中，然后對種群中的個體進行擾動和組合，通過應用變異和交叉算子產生新的候選種群。新的種群是通過在當前種群和新的候選種群中選擇更好的個體而產生的。整個過程重復進行，直到滿足終止準則為止。本節采用差分進化算法來解決式（20）中的優化問題。

差分進化算法和待解決的優化問題之間的關系模型可表示如下：

A_i，G=（l_1，i，G，l_2，i，G，l_3，i，G，l_4，i，G）

l_j，min=l_1，min， l_j，max=l_1，max， j=1

l_j，min=l_2，min， l_j，max=l_2，max， j=2

l_j，min=l_3，min， l_j，max=l_3，max， j=3

l_j，min=l_4，min， l_j，max=l_4，max， j=4

D=4（24）

式中：A_i，G是第G代種群的第i（i=1，2，…，N）個個體，由l_1，i，G、l_2，i，G、l_3，i，G、l_4，i，G 4個分量組成；N為種群大小;D表示搜索空間維數;下標j（j=1，2，3，4）表示個體的第j個分量;l_j，max和l_j，min分別表示參數l_j的最大值和最小值。

差分進化算法的具體步驟如下。

步驟 1 種群初始化。初始化種群需要在規定的最小值和最大值范圍內隨機產生N個個體，每個個體中各分量的計算公式如下：

l_j，i，0=l_j，min+rand_i，j［0，1］·（l_j，max－l_j，min）， j=1，2，3，4（25）

參數l_j的最大值和最小值可根據目標運動參數的取值范圍以及式（4）～式（7）確定。本文假設地面運動目標沿x軸、y軸的速度的取值范圍是-30～30 m/s，沿x軸、y軸的加速度的取值范圍是-1～1 m/s²。

步驟 2 變異。從種群中隨機選取3個不同的個體A_ri1，G、A_ri2，G、A_ri3，G，并產生變異個體：

V_i，G=A_ri1，G+F·（A_ri2，G－A_ri3，G）（26）

式中：F是變異因子。

步驟 3 交叉。交叉所得個體U_i，G的第j個分量u_j，i，G產生如下：

u_j，i，G=v_j，i，G， rand_i，j［0，1］≤Cr或j=j_rand

l_j，i，G， 其他（27）

式中：v_j，i，G為變異個體的第j個分量;Cr為交叉因子;j_rand為1到4之間的一個隨機整數，以保證交叉后的個體至少有一個分量來自變異個體。

步驟 4 計算適應度函數。由于優化問題是基于目標圖像對比度的最大化，因此選擇某一個體對應的參數所聚焦圖像的對比度作為該個體的適應度值。通過式（22）得到圖像，通過式（21）計算對比度。

步驟 5 選擇。差分進化算法使用貪婪算法，根據適應度函數的值，從種群中選擇更優的個體作為下一代的初始種群，具體選擇方式為

A_i，G+1=U_i，G， Contrast（U_i，G）≥Contrast（A_i，G）

A_i，G， Contrast（U_i，G）lt;Contrast（A_i，G）（28）

步驟 6 重復執行步驟2～步驟5，直到滿足終止條件或達到最大迭代次數，最大對比度值所對應的參數即為優化問題的解。

利用差分進化算法求解式（20）所示優化問題的流程圖如圖3所示。

2.3 成像流程

本文所提出的成像算法流程圖如圖4所示。首先，將目標信號變換到二維頻域。接著，利用差分進化算法求解式（20）所示的優化問題，估計出構建濾波器所需的參數。最后，利用得到的最優解，通過式（23）對目標進行聚焦。本文方法假設目標信號已被提取出。

3 實驗結果

3.1 參數搜索結果

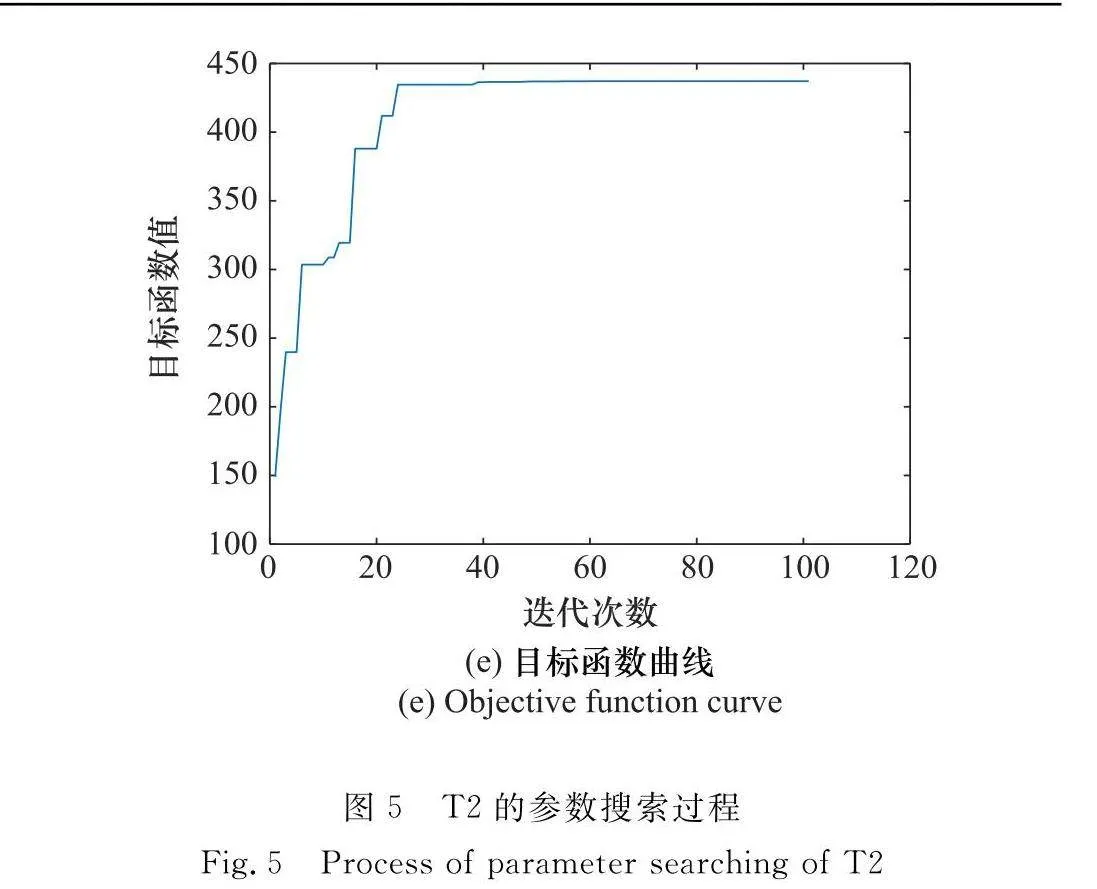
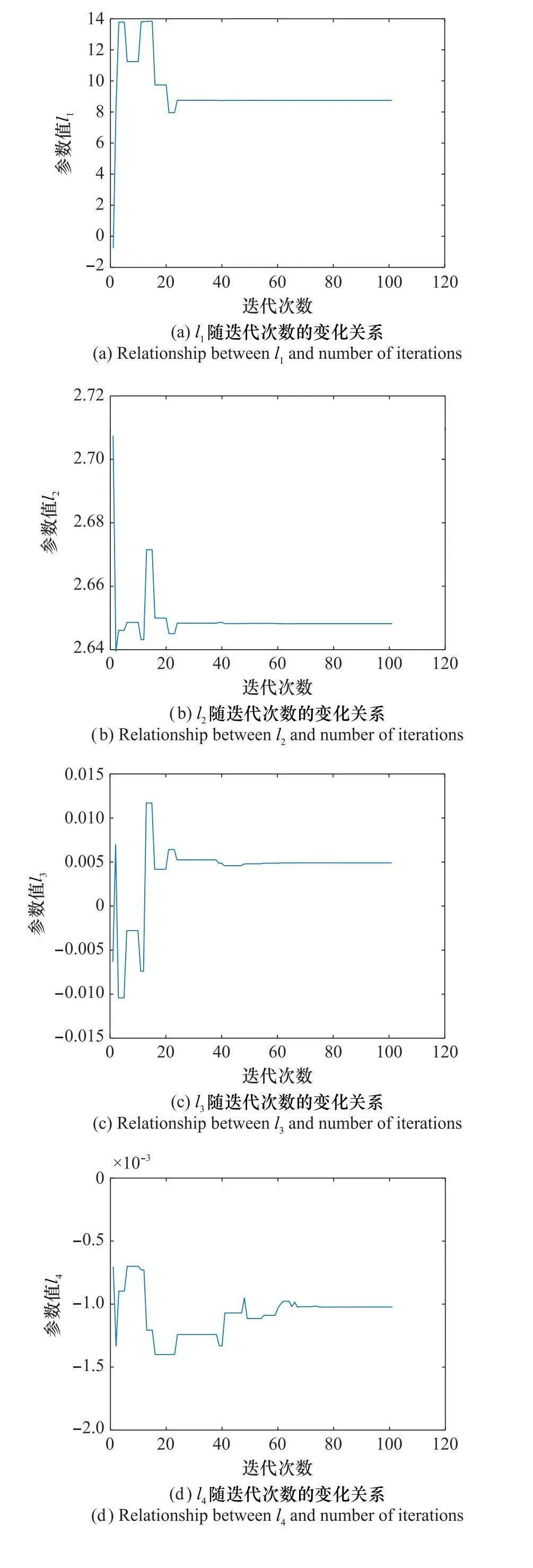
本節驗證基于差分進化算法的參數搜索的有效性。表1為CSSAR系統參數，表2為目標參數。差分進化算法的種群大小N=50，迭代次數G=100，變異因子F=0.5，交叉因子Cr=0.9。表3～表5給出了每個目標參數搜索的結果。可以看到，每個目標距離方程的4個參數都被準確估計出來了。以目標T2為例，圖5給出了差分進化的參數搜索過程，包括適應度函數曲線和4個參數隨迭代次數的變化關系圖。從圖5可以看出，迭代過程收斂較快。

3.2 目標成像結果

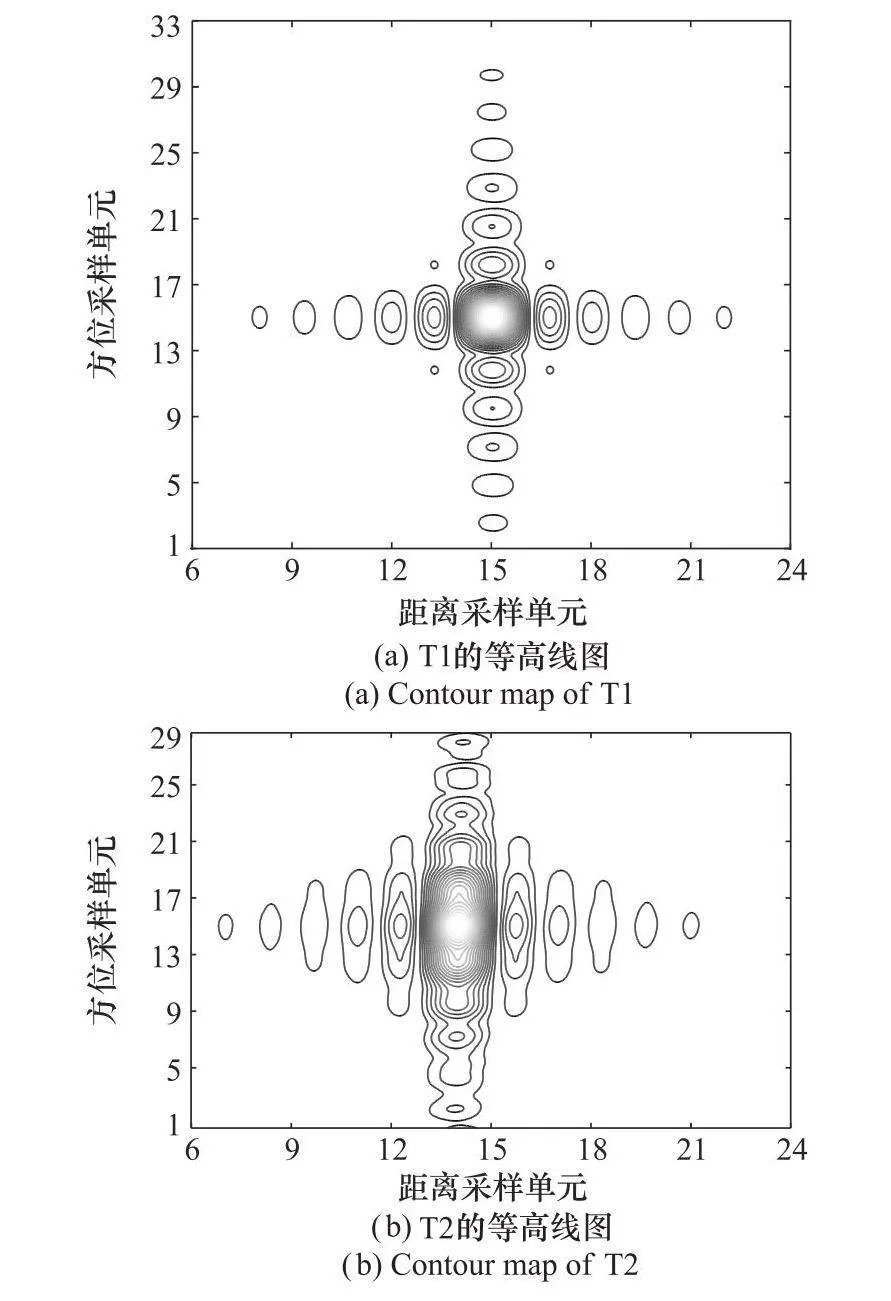
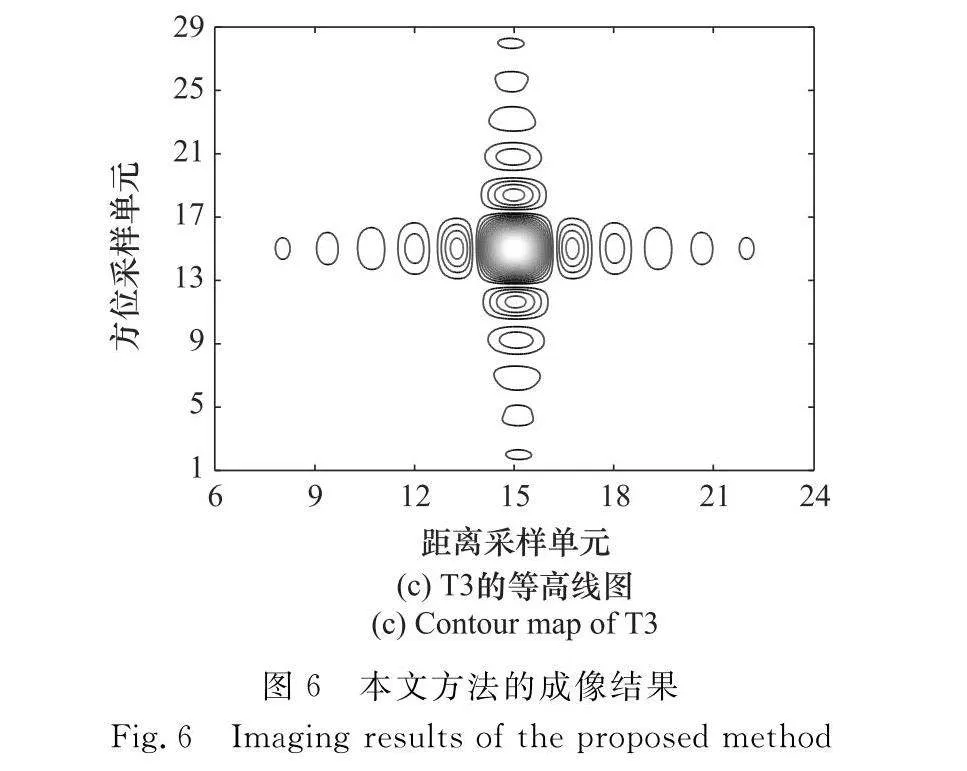
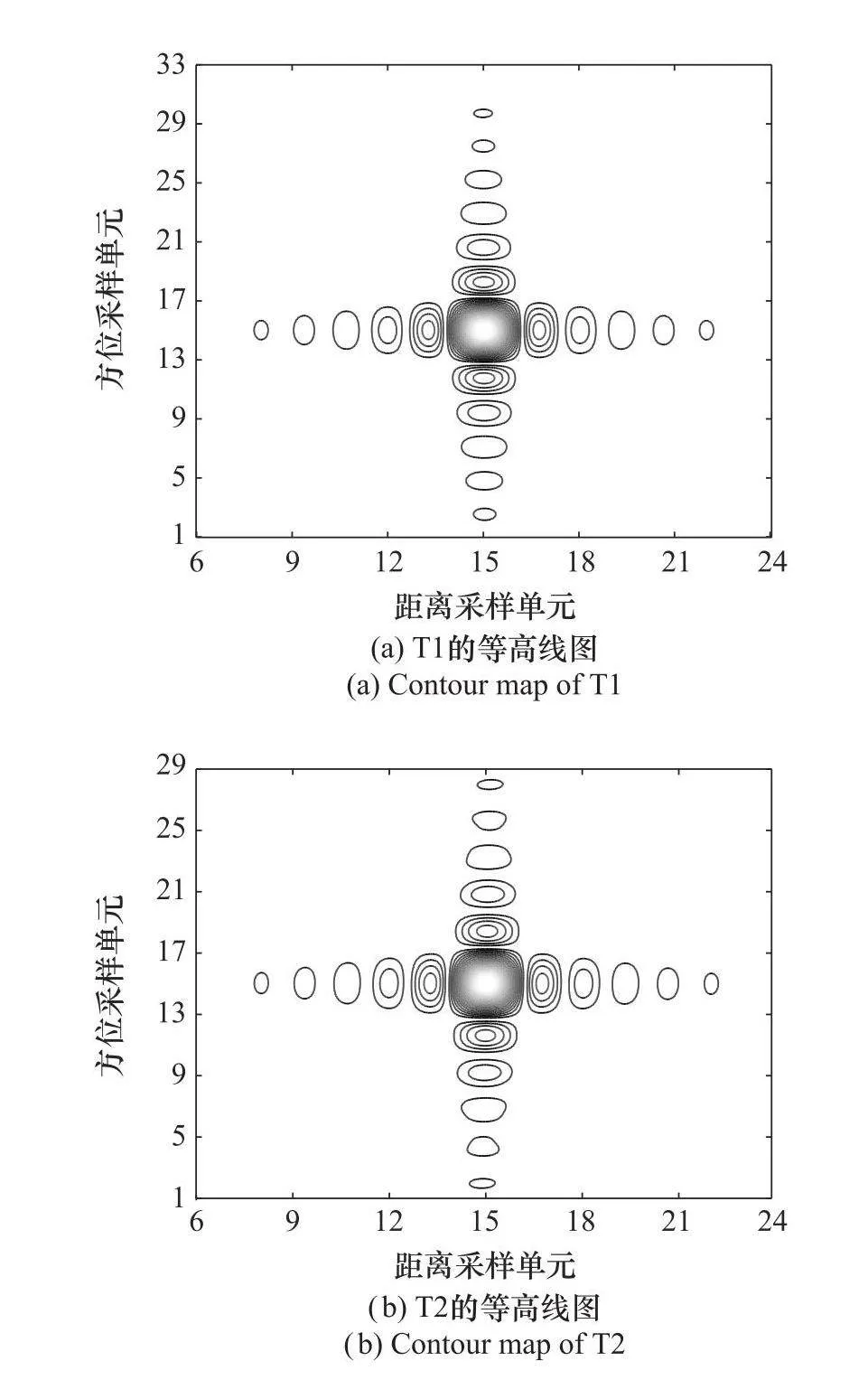
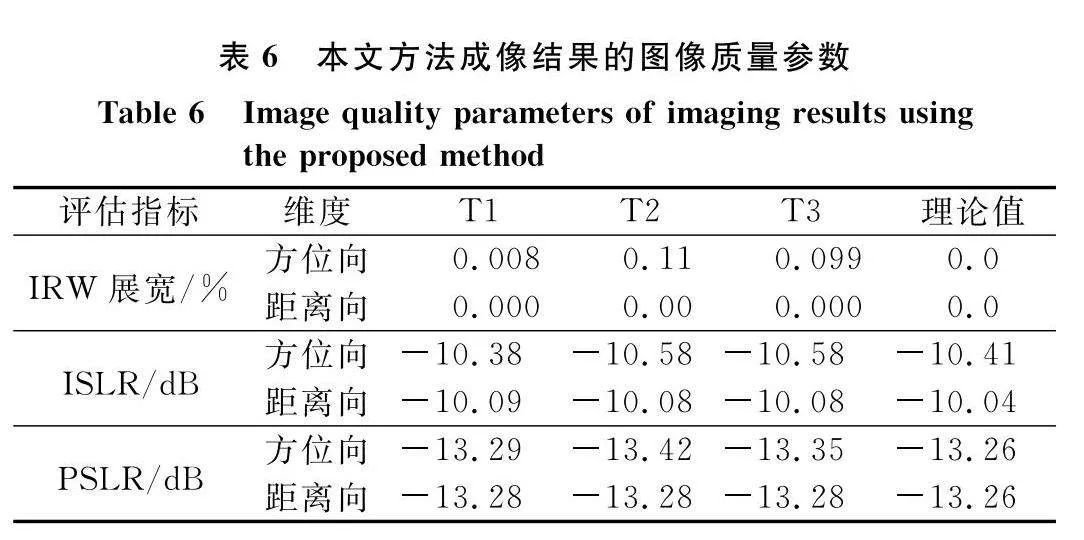
首先對第3.1節的3個運動目標，利用差分進化算法搜索出的參數基于式（23）進行成像，并測量了圖像質量參數。圖6為目標成像結果，表6為每個圖像的質量參數。根據上述實驗結果可以看出，3個目標都得到了很好的聚焦，而且每個目標的圖像質量參數都與理論值非常接近，說明成像質量很好。

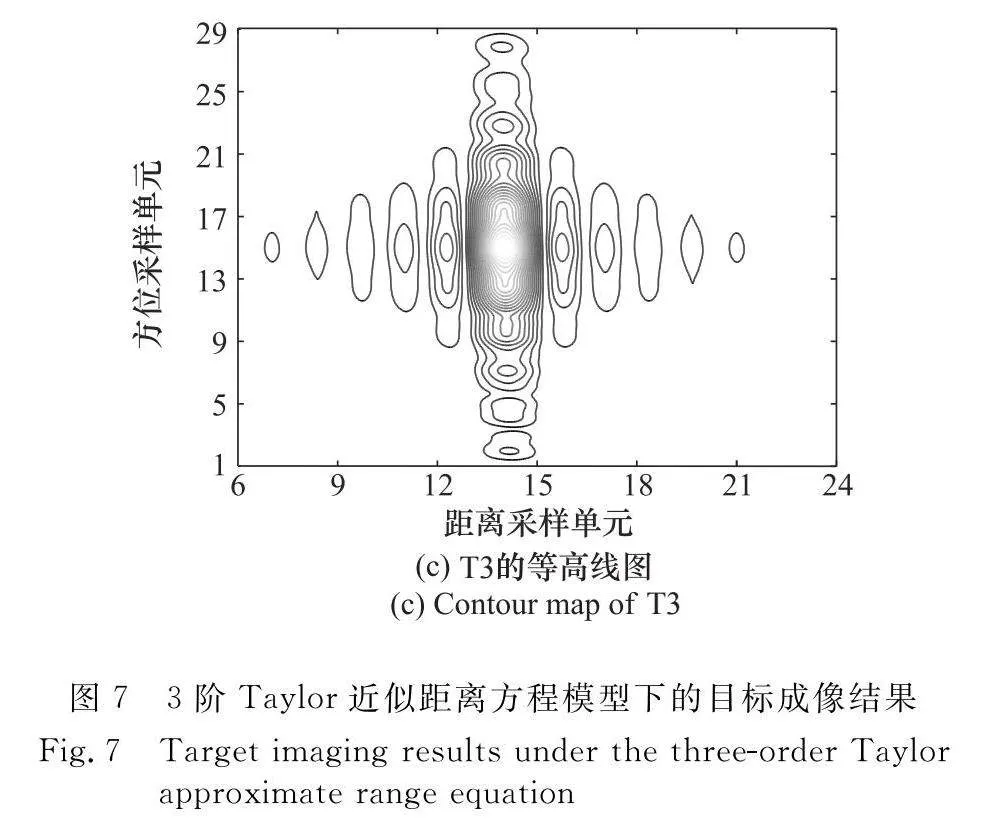
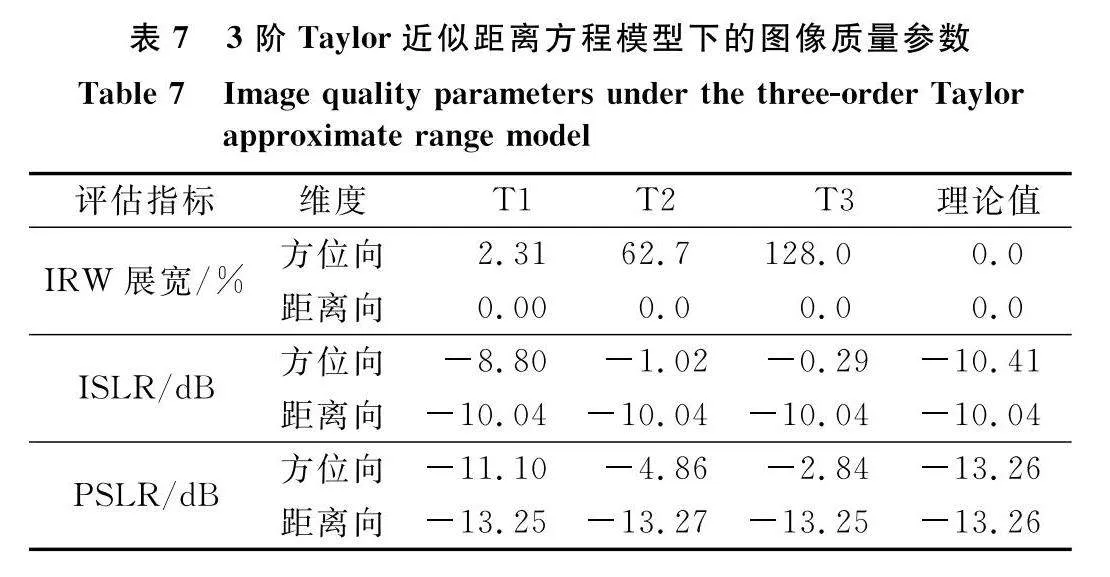
為了更好地說明本文方法的成像效果，針對同樣的3個目標，利用3階Taylor近似距離方程進行成像（假設目標參數精確已知），圖7給出了這些目標的成像效果。同時，也測量了圖像質量參數，如表7所示。從圖7和表7可以看出，目標出現了明顯的散焦，成像質量不好。這是由3階Taylor近似距離方程過大的相位誤差所致。

為了說明本文方法參數搜索的高效性，本文還對比了本文方法與文獻［23］所提方法的運行時間。實驗結果表明，本文方法運行時間為6.85 min，文獻［23］的方法運行時間為20.03 min。可以看出，本文方法的效率更高，這是因為差分進化算法能高效地實現對各參數的搜索。

4 結 論

本文為機載高分辨CSSAR-GMTI系統，提出一種地面加速運動目標成像方法。針對圓軌跡和高分辨導致目標距離方程高階分量顯著的問題，本文建立了4階Taylor近似距離模型。為了提高計算效率，本文提出在二維頻域通過相位相乘來實現聚焦，并利用差分進化算法來提升成像過程中參數搜索的效率。最終，通過實驗驗證了所提方法能夠滿足高分辨系統對地面加速運動目標精確成像的要求。

參考文獻

［1］ 洪文， 胡東輝， 韓冰， 等. 合成孔徑雷達成像—算法與實現［M］. 北京： 電子工業出版社， 2007.

HONG W， HU D H， HAN B， et al. Digital processing of synthetic aperture radar data algorithms and implementation［M］. Beijing： Publishing House of Electronics Industry， 2007.

［2］ MOREIRA A， PRATS I P， YOUNIS M， et al. A tutorial on synthetic aperture radar［J］. IEEE Geoscience and Remote Sensing Magazine， 2013， 1（1）： 643.

［3］ 李鉑宇， 陳濺來， 孫光才， 等. 結合通道均衡的SAR距離DBF方法［J］. 系統工程與電子技術， 2019， 41（3）： 523528.

LI B Y， CHEN J L， SUN G C， et al. SAR range DBF method combined with channel equalization［J］. Systems Engineering and Electronics， 2019， 41（3）： 523528.

［4］ CHEN H M， LI Y C， GAO W Q， et al. Bayesian forward-looking superresolution imaging using Doppler deconvolution in expanded beam space for high-speed platform［J］. IEEE Trans.on Geoscience and Remote Sensing， 202 60： 5105113.

［5］ XU G， ZHANG B J， YU H W， et al. Sparse synthetic aperture radar imaging from compressed sensing and machine learning： theories， applications and trends［J］. IEEE Geoscience and Remote Sensing Magazine， 202 10（4）： 3269.

［6］ 王寧， 賀鵬超， 盧景月， 等. 基于DOA估計的前視多通道SAR成像方法［J］. 系統工程與電子技術， 2023， 45（8）： 24712478.

WANG N， HE P C， LU J Y， et al. DOA estimation based imaging method for multi-channel forward-looking SAR［J］. Systems Engineering and Electronics， 2023， 45（8）： 24712478.

［7］ ENDER J H G， GIERULL C H， CERUTTI-MAORI D. Improved space-based moving target indication via alternate transmission and receiver switching［J］. IEEE Trans.on Geoscience and Remote Sensing， 2008， 46（12）： 39603974.

［8］ GAO G， HUANG K H， GAO S， et al. Ship detection based on oceanic displaced phase center antenna technique in along-track interferometric SAR［J］. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing， 2019， 12（3）： 788802.

［9］ 李相海， 楊志偉， 賀順， 等. 基于路網信息輔助的多星編隊系統SAR-GMTI動目標徑向速度估計與重定位方法［J］. 系統工程與電子技術， 2023， 45（3）： 629637.

LI X H， YANG Z W， HE S， et al. Method for SAR-GMTI moving target radial velocity estimation and relocation based on road network information assistance in multi-satellite formation system［J］. Systems Engineering and Electronics， 2023， 45（3）： 629637.

［10］ GUO Y F， LIAO G S， LU J， et al. A novel moving target detection method based on RPCA for SAR systems［J］. IEEE Trans.on Geoscience and Remote Sensing， 2020， 58（9）： 66776690.

［11］ HAN C L， YANG Z W， LIAO G S， et al. A SAR-GMTI approach aided by online knowledge with an airborne multichannel Quad-Pol radar system［J］. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing， 202 15： 86688681.

［12］ SJOGREN T K， VU V T， PETTERSSON M I， et al. Change detection for monostatic pursuit SAR GMTI-theories and experimental results［J］. IEEE Trans.on Geoscience and Remote Sensing， 202 60： 5235514.

［13］ 熊世超， 倪嘉成， 張群， 等. 基于頻譜旋轉ωk算法的大斜視SAR地面動目標成像［J］. 系統工程與電子技術， 202 44（10）： 31043114.

XIONG S C， NI J C， ZHANG Q， et al. High-squint mode SAR GMTI-based on ωk algorithm with spectrum rotation［J］. Systems Engineering and Electronics， 202 44（10）： 31043114.

［14］ CHEN Z Y， TANG S Y， REN Y， et al. Curvilinear flight synthetic aperture radar （CF-SAR）： principles， methods， applications， challenges and trends［J］. Remote Sensing， 202 14（13）： 2983.

［15］ ZHANG Y， ZHU D Y， MAO X H， et al. Multirotor UAV-borne repeat-pass CSM-videoSAR［J］. IEEE Trans.on Aerospace and Electronic Systems， 202 58（3）： 26012605.

［16］ BAUMGARTNER S V. Circular and polarimetric ISAR imaging of ships using airborne SAR sensors［C］∥Proc.of the 12th European Conference on Synthetic Aperture Radar， 2018.

［17］ LIAO Y， WANG W Q， LIU Q H. Two-dimensional spectrum for circular trace scanning SAR based on an implicit function［J］. IEEE Geoscience and Remote Sensing Letters， 2016， 13（7）： 887891.

［18］ 李永康. 機載條帶SAR動目標成像與機載CSSAR動目標檢測方法研究［D］. 西安： 西安電子科技大學， 2016.

LI Y K. Study on airborne stripmap SAR ground moving target imaging and airborne CSSAR GMTI［D］. Xi’an： Xidian University， 2016.

［19］ LI Y K， WANG Y L， LIU B C， et al. A new motion parameter estimation and relocation scheme for airborne three-channel CSSAR-GMTI systems［J］. IEEE Trans.on Geoscience and Remote Sensing， 2019， 57（6）： 41074120.

［20］ ZHANG Y， ZHU D Y， MAO X H， et al. Multirotors video synthetic aperture radar： system development and signal processing［M］. IEEE Aerospace and Electronic Systems Magazine， 2020， 35（12）： 3243.

［21］ SONG C， WANG B N， XIANG M S， et al. A novel imaging-based target detection and parameter estimation scheme for airborne multichannel circular stripmap SAR［J］. IEEE Trans.on Geoscience and Remote Sensing， 2023， 61： 5203515.

［22］ JAO J K， YEGULALP A. Multichannel synthetic aperture radar signatures and imaging of a moving target［J］. Inverse Problem， 2013， 29（5）： 054009.

［23］ YANG J， LIU C， WANG Y F. Imaging and parameter estimation of fast-moving targets with single-antenna SAR［J］. IEEE Geoscience and Remote Sensing Letters， 2014， 11（2）： 529533.

［24］ LI D， ZHAN M Y， SU J， et al. Performances analysis of coherently integrated CPF for LFM signal under low SNR and its application to ground moving target imaging［J］. IEEE Trans.on Geoscience and Remote Sensing， 2017， 55（11）： 64026419.

［25］ ZENG C， LI D， LUO X， et al. Ground maneuvering targets imaging for synthetic aperture radar based on second-order keystone transform and high-order motion parameter estimation［J］. IEEE Journal of Selected Topics in Signal Processing， 2019， 12（11）： 44864501.

［26］ HUANG P H， LIAO G S， YANG Z W， et al. Ground maneuvering target imaging and high-order motion parameter estimation based on second-order keystone and generalized Hough-HAF transform［J］. IEEE Trans.on Geoscience and Remote Sensing， 2017， 55（1）： 320335.

［27］ YANG L， ZHAO L F， BI G A， et al. SAR ground moving target imaging algorithm based on parametric and dynamic sparse Bayesian learning［J］. IEEE Trans.on Geoscience and Remote Sensing， 2016， 54（4）： 22542267.

［28］ DU H G， SONG Y P， JIANG N， et al. A novel SAR ground maneuvering target imaging method based on adaptive phase tracking［J］. IEEE Trans.on Geoscience and Remote Sensing， 2023， 61： 5211916.

［29］ CARRARA W G， GOODMAN R S， MAJEWSKI R M. Spotlight synthetic aperture radar signal processing algorithms［M］. New York： Artech House， 1995.

［30］ DAS S， SUGANTHAN P N. Differential evolution： a survey of the state-of-the-art［J］. IEEE Trans.on Evolutionary Computation， 201 15（1）： 431.

作者簡介

李永康（1988—），男，副教授，博士，主要研究方向為合成孔徑雷達、運動目標指示、雷達成像。

朱濟榮（2001—），男，碩士研究生，主要研究方向為合成孔徑雷達。

楊晨茜（1998—），女，碩士，主要研究方向為合成孔徑雷達。