動態(tài)拓撲下四旋翼無人機集群蜂擁控制

摘 要：針對動態(tài)拓撲下無嚴(yán)格構(gòu)型約束的無人機集群協(xié)同控制問題，基于四旋翼無人機（quadrotor unmanned aerial vehicle， QUAV）內(nèi)外環(huán)串級控制思想，提出一種QUAV集群蜂擁控制策略。引入卡爾曼一致性濾波（Kalman-consensus filter， KCF）算法對帶有噪聲的通信數(shù)據(jù)進行融合，實現(xiàn)對變速度領(lǐng)導(dǎo)者狀態(tài)的精確估計;考慮無人機集群拓撲的動態(tài)變化及可擴展性需求，設(shè)計基于KCF的蜂擁控制算法以實現(xiàn)無人機集群位置控制，利用李雅普諾夫穩(wěn)定性定理證明算法的穩(wěn)定性;基于大腦情感學(xué)習(xí)（brain emotional learning， BEL）模型設(shè)計姿態(tài)控制器，實現(xiàn)了QUAV的姿態(tài)控制。通過仿真實驗驗證了控制算法的有效性。

關(guān)鍵詞： 無人機集群; 蜂擁控制; 動態(tài)拓撲; 卡爾曼一致性濾波; 大腦情感學(xué)習(xí)

中圖分類號： V 279 文獻標(biāo)志碼： A""" DOI：10.12305/j.issn.1001-506X.2024.10.24

Flocking control for quadrotor unmanned aerial vehicle swarm with dynamic topology

YIN Yaxuan， ZHANG An， BI Wenhao YANG Pan， HUANG Zhanjun

（School of Aeronautics， Northwestern Polytechnical University， Xi’an 71007 China）

Abstract： In view of the cooperative control problem of unmanned aerial vehicle （UAV） swarm without strict configuration constraints under dynamic topology， a flocking control strategy of quadrotor UAV （QUAV） swarm is proposed on the basis of cascade control idea of the inner-outer loop of QUAV. The Kalman-consensus filter （KCF） algorithm is utilized to fuse the communication data with noise， which realizes the accurate estimation of the state of leader with varying velocity. Considering the dynamic variation and scalability requirements of UAV swarm， a flocking control algorithm based on the KCF is designed to realize the position control for the UAV swarm. The stability of the proposed algorithm is proved by the Lyapunov stability theory. An attitude controller is designed for QUAV based on brain emotional learning （BEL） model， which enables the pose control for QUAV. Simulation results prove the validity of control algorithm.

Keywords： unmanned aerial vehicle （UAV） swarm; flocking control; dynamic topology; Kalman-consensus filter （KCF）; brain emotional learning （BEL）

0 引 言

隨著無人系統(tǒng)技術(shù)的飛速發(fā)展，分布式無人機集群協(xié)同作戰(zhàn)以其低成本、大規(guī)模的優(yōu)勢成為未來戰(zhàn)爭的重要作戰(zhàn)樣式之一^［12］。無人機集群可遂行區(qū)域偵察、火力打擊、電子對抗等多類任務(wù)，憑借其極高的效費比大量消耗對方作戰(zhàn)力量，為后續(xù)作戰(zhàn)行動創(chuàng)造更多戰(zhàn)機。

無人機集群協(xié)同控制是無人機集群作戰(zhàn)的重要一環(huán)。文獻［3］面向飽和攻擊問題設(shè)計改進一致性算法，降低任務(wù)損耗，并提高任務(wù)效率;文獻［4］針對無人機集群打擊海面運動目標(biāo)任務(wù)提出一種固定時間協(xié)同控制方法，實現(xiàn)了期望編隊構(gòu)型的形成與保持;文獻［5］提出一種基于分層控制框架的多無人機分組編隊跟蹤控制策略，實現(xiàn)無人機集群多目標(biāo)偵察任務(wù)。無人機集群協(xié)同控制過程一般涉及兩種拓撲，一種為通信拓撲，指無人機間的通信連接關(guān)系;另一種為任務(wù)構(gòu)型拓撲，即無人機集群根據(jù)任務(wù)需求形成特定的功能拓撲結(jié)構(gòu)。上述文獻大多面向固定的任務(wù)構(gòu)型展開，且通信拓撲相對固定，不具有良好的可擴展性。在集群實際作戰(zhàn)過程中，部分任務(wù)對集群的任務(wù)構(gòu)型沒有嚴(yán)格約束，但需考慮運動過程中數(shù)據(jù)丟包、節(jié)點失效等情況引起的通信拓撲動態(tài)變化。此外，上述控制協(xié)議的設(shè)計多假設(shè)無人機可直接獲得所需的實際運動狀態(tài)信息，并未考慮實際通信過程中存在的噪聲和不確定性數(shù)據(jù)的影響。

在通信和計算資源有限的情況下，蜂擁控制僅依靠簡單的個體行為準(zhǔn)則和有限的信息交互，就能在無全局控制、無構(gòu)型約束的情況下，展現(xiàn)出強大的同步效應(yīng)。文獻［6］首先提出3條運動規(guī)則，即：群體聚合、碰撞避免及速度匹配，并以此定義一種群體蜂擁模型。在此基礎(chǔ)上，研究人員建立一系列數(shù)學(xué)模型，對蜂擁過程的本質(zhì)加以描述，如Vicsek模型^［7］、Cucker-Smale模型^［8］、Olfati-Saber算法^［9］等。針對動態(tài)拓撲下的多智能體蜂擁控制問題，文獻［10］提出一種動態(tài)牽制控制算法，以實現(xiàn)動態(tài)拓撲下不考慮初始時刻網(wǎng)絡(luò)連通性的蜂擁控制;文獻［11］設(shè)計一種局部自適應(yīng)牽制控制算法，實現(xiàn)具有變速度虛擬領(lǐng)導(dǎo)者的蜂擁控制;文獻［12］考慮輸入延遲情況，實現(xiàn)動態(tài)拓撲下混合事件觸發(fā)脈沖控制的強非線性多智能體蜂擁控制。進一步考慮噪聲的影響，文獻［13］提出一種補償期望速度的自適應(yīng)協(xié)議，實現(xiàn)噪聲環(huán)境中對領(lǐng)導(dǎo)者速度的準(zhǔn)確跟蹤;文獻［1415］引入分布式卡爾曼一致性濾波器進行數(shù)據(jù)融合，以獲取更精確的領(lǐng)導(dǎo)者運動狀態(tài)信息;文獻［16］在此基礎(chǔ)上進一步研究連續(xù)時間下的信息加權(quán)卡爾曼一致性濾波器，并將其與蜂擁控制算法耦合，進一步提高控制的精確性;文獻［17］則研究具有變速度的領(lǐng)導(dǎo)者的狀態(tài)估計與跟蹤問題。在無人機集群蜂擁控制方面，文獻［18］研究無人機集群的分層加權(quán)Vicsek模型，引入分層調(diào)節(jié)機制與分層加權(quán)機制，以實現(xiàn)高性能避障控制，并提高算法收斂速度;文獻［19］提出基于改進鴿群優(yōu)化算法的無人機集群蜂擁控制，將避障問題轉(zhuǎn)化為多目標(biāo)優(yōu)化問題，實現(xiàn)復(fù)雜環(huán)境下的集群避障控制;文獻［20］提出基于并行觸發(fā)機制的無人機集群蜂擁控制，以進一步節(jié)省通信資源。目前有關(guān)四旋翼無人機（quadrotor unmanned aerial vehicle， QUAV）集群蜂擁控制的研究多將無人機個體視為質(zhì)點，針對其位置回路進行蜂擁控制算法設(shè)計，很少引入QUAV動力學(xué)模型，實現(xiàn)考慮姿態(tài)控制的六自由度無人機集群蜂擁控制。

QUAV具有強耦合、非線性、欠驅(qū)動等特性^［21］，在姿態(tài)控制方面，目前已有比例積分微分（proportion-integration-differentiation， PID）控制^［22］、反步法^［23］、自抗擾控制^［24］、滑模控制^［25］等多種實現(xiàn)方法。特別地，文獻［26］中提出一種基于大腦情感學(xué)習(xí)智能控制器（brain emotional learning based intelligent controller， BELBIC）的控制系統(tǒng)，有效實現(xiàn)了變推力軸線無人機的姿態(tài)控制。基于大腦情感學(xué)習(xí)（brain emotional learning， BEL）模型的QUAV姿態(tài)控制有控制參數(shù)自學(xué)習(xí)、自整定的能力，能較好地處理系統(tǒng)的非線性問題，具有計算簡單、對實時系統(tǒng)計算資源要求低的特點。

綜上所述，本文旨在設(shè)計一種QUAV集群蜂擁控制策略，以實現(xiàn)動態(tài)拓撲下的無人機集群協(xié)同控制。針對通信過程中的噪聲和不確定性數(shù)據(jù)對無人機獲取領(lǐng)導(dǎo)者準(zhǔn)確運動狀態(tài)信息的影響，通過卡爾曼一致性濾波算法進行信息融合以實現(xiàn)噪聲抑制;針對實際任務(wù)過程中的可擴展性需求，設(shè)計動態(tài)拓撲下具有變速度領(lǐng)導(dǎo)者的無人機集群蜂擁控制算法;同時基于BELBIC姿態(tài)控制器實現(xiàn)QUAV個體的姿態(tài)控制，最終實現(xiàn)六自由度的QUAV集群蜂擁控制。

本文結(jié)構(gòu)如下：第1節(jié)建立QUAV動力學(xué)模型及集群通信模型;第2節(jié)設(shè)計QUAV集群蜂擁控制策略;第3節(jié)設(shè)計基于卡爾曼一致性濾波的無人機集群蜂擁控制算法;第4節(jié)設(shè)計基于BELBIC的QUAV姿態(tài)控制器;第5節(jié)進行數(shù)值仿真驗證;第6節(jié)得出結(jié)論。

1 模型建立與問題描述

1.1 QUAV動力學(xué)模型

QUAV是一個強耦合、欠驅(qū)動的非線性系統(tǒng)。針對QUAV的實際運動特性，在無風(fēng)或小風(fēng)速環(huán)境中，忽略空氣阻力引起的影響，得到簡化的QUAV動力學(xué)模型^［27］如下：

q¨_x=U₁（sin θcos φcos +sin φsin ）

m

q¨_y=U₁（sin θcos φsin －sin φcos ）m

q¨_z=U₁（cos φcos θ）m－g

φ¨=1I_x［U₂+（I_y－I_z）φ··］

θ¨=1I_y［U₃+（I_z－I_x）·θ·］

¨=1I_z［U₄+（I_x－I_y）φ·θ·］（1）

式中：q¨_x，q¨_y，q¨_z分別為無人機在地面坐標(biāo)系x軸、y軸、z軸上的加速度;為無人機的偏航角;θ為俯仰角;φ為滾轉(zhuǎn)角;m為無人機的質(zhì)量;I_x，I_y，I_z分別表示QUAV對應(yīng)軸上的轉(zhuǎn)動慣量;φ·，θ·，·可分別近似為對應(yīng)軸的機體角速率;U₁，U₂，U₃，U₄分別為高度、俯仰、滾轉(zhuǎn)、偏航4個通道控制量，其定義為

U₁=∑4i=1T_i

U₂=（－T₂+T₄）l

U₃=（－T₁+T₃）l

U₄=－Q_q1+Q_q2－Q_q3+Q_q4（2）

式中：T_i為螺旋槳產(chǎn)生的升力;Q_qi為螺旋槳產(chǎn)生的反扭矩;l為無人機質(zhì)心到旋翼旋轉(zhuǎn)軸之間的距離。

1.2 系統(tǒng)數(shù)學(xué)描述

考慮由n架無人機構(gòu)成無人機集群，記無人機i的運動方程為

q·_i（t）=p_i（t）

p·i（t）=u_i（t）（3）

式中：q_i，p_i，u_i∈R^d（i=1，2，…，n）分別為無人機i的位置向量、速度向量及控制輸入。

記領(lǐng)導(dǎo)者的運動方程為

q·_γ（t）=p_γ（t）

p·γ（t）=u_γ（t）（4）

式中：q_γ，p_γ，u_γ∈R^d分別為領(lǐng)導(dǎo)者的位置向量、速度向量及控制輸入。

集群中無人機基于卡爾曼一致性濾波算法對領(lǐng)導(dǎo)者的運動狀態(tài)進行估計。記領(lǐng)導(dǎo)者的狀態(tài)方程為

x·（t）=Ax（t）+Bω（t）（5）

無人機i的觀測方程為

z_i（t）=H_ix（t）+v_i（t）（6）

式中：x=［q_γ;p_γ;u_γ］∈R^m為待估計的領(lǐng)導(dǎo)者運動狀態(tài);A，B∈R^m×m分別為領(lǐng)導(dǎo)者的狀態(tài)轉(zhuǎn)移矩陣和噪聲輸入矩陣;z_i∈R^p為無人機i對領(lǐng)導(dǎo)者運動狀態(tài)的觀測值;H_i∈R^p×m為無人機i的觀測矩陣;ω和v_i分別為過程噪聲和測量噪聲，均為零均值高斯白噪聲，且協(xié)方差分別為

Cov（ω（k）ω（l）T）=Qδ_kl（7）

Cov（v_i（k）v_j（l）T）=R_iδ_klδ_ij（8）

式中：Q∈R^m×m，R_i∈R^p×p均為主對角線元素大于0的對角矩陣。當(dāng)k=l時，δ_kl=1;否則，δ_kl=0。

1.3 無人機集群網(wǎng)絡(luò)模型

QUAV集群系統(tǒng)可由節(jié)點數(shù)為n的無向圖G（t）=（V，E（t））表示。定義無向圖的有限節(jié)點集為V={1，2，…，n}，連接節(jié)點的邊的集合為E（t）={e（t）_ij=（i，j），i，j∈V}。

考慮無人機通信距離和傳感器檢測距離有限的情況，無人機i僅能與其鄰域內(nèi)無人機進行信息交流，而無法獲取鄰域外無人機的狀態(tài)信息。假設(shè)集群中各無人機間的極限交互距離相同且均為d_max，則無人機i的鄰居集定義為

N_i（t）={j|q_i－q_jlt;d_max， j≠i，j=1，2，…，n}（9）

式中：·表示向量的歐氏距離。

若無人機i與無人機j互為鄰居，則其對應(yīng)節(jié)點之間存在邊;反之，則不存在。鄰接矩陣A_d（G）=（a_ij（t））_n×n表示集群中各無人機的連接情況：若j∈N_i，則a_ij（t）=1;反之，a_ij（t）=0。

1.4 問題描述

以無人機集群遂行壓制防空（suppression of enemy air defense， SEAD）任務(wù)為背景^［2829］構(gòu)建研究問題。考慮由n架同構(gòu)QUAV與一個領(lǐng)導(dǎo)者組成系統(tǒng)，執(zhí)行對區(qū)域目標(biāo)的搜索、識別和確認任務(wù)，同時實現(xiàn)對對方區(qū)域的實時監(jiān)控。無人機集群飛行過程中無固定編隊構(gòu)型要求，需考慮通信拓撲結(jié)構(gòu)的動態(tài)變化及在噪聲環(huán)境中對領(lǐng)導(dǎo)者運動狀態(tài)進行跟蹤。

集群中各無人機初始時刻的位置與速度均處于隨機無序狀態(tài);領(lǐng)導(dǎo)者的影響范圍固定，且僅在與其距離不超過R_max的區(qū)域中的無人機能夠獲取領(lǐng)導(dǎo)者的運動狀態(tài)信息。基于無人機集群蜂擁控制算法實現(xiàn)動態(tài)拓撲下無嚴(yán)格構(gòu)型約束的可擴展無人機集群協(xié)同控制，系統(tǒng)最終狀態(tài)滿足下列條件：

（1） 無人機集群中各無人機速度趨于一致

limt→∞p_i－p_j=0（10）

（2） 無人機集群中無人機間距離有界

sup0≤tlt;∞q_i－q_jlt;∞（11）

（3） 在運動過程中，所有無人機間無碰撞

q_i（t）－q_j（t）gt;0（12）

1.5 相關(guān)引理

引理 1^［30］ 矩陣L為連通無向圖的對稱拉普拉斯矩陣，設(shè)矩陣H_d=diag（h₁，h₂，…，h_n）為對角矩陣，其元素滿足h_i≥0（i=1，2，…，n），若對角矩陣H_d中至少存在一個正元素，那么矩陣L+H_d的所有特征值都是正的。

引理 2^［31］ 考慮自治系統(tǒng)：

x·=f（x）（13）

式中：x∈R^m;f：D→R^m為從定義域DR^m到R^m的局部李普希茨映射。設(shè)ΩD為式（13）的一個正不變緊集。設(shè)V：D→R是連續(xù)可微函數(shù)，在Ω內(nèi)滿足V·≤0。設(shè)E_Ω是Ω內(nèi)所有點的集合，滿足V·=0，M為E_Ω內(nèi)的最大不變集。則t趨于無窮時，起始于Ω內(nèi)的每個解都趨于M。

2 QUAV集群蜂擁控制策略

針對六自由度QUAV集群蜂擁控制問題提出雙環(huán)控制方案，其結(jié)構(gòu)如圖1所示。基于QUAV內(nèi)外環(huán)串級控制的理念，對QUAV的位置控制回路和姿態(tài)控制回路進行解耦，進而將六自由度QUAV集群蜂擁控制問題轉(zhuǎn)化為位置控制回路的蜂擁控制問題和姿態(tài)控制回路的指令跟蹤問題。同時，為降低無人機間信息傳輸過程中噪聲和不確定性數(shù)據(jù)的影響，引入卡爾曼一致性濾波算法對領(lǐng)導(dǎo)者的運動狀態(tài)信息進行融合，以實現(xiàn)噪聲抑制。

QUAV通過調(diào)整姿態(tài)角改變位置回路加速度，進而實現(xiàn)位置控制。依據(jù)式（1）中位置回路動態(tài)方程，引入無人機i的虛擬控制量：

u_ix=1m（sin θ_icos φ_icos _i+sin φ_isin _i）U_1i

u_iy=1m（sin θ_icos φ_isin _i－sin φ_icos _i）U_1i

u_iz=1m（cos φ_icos θ_i）U_1i－g（14）

進而可由虛擬控制量u_ix、u_iy、u_iz反推出所需的期望姿態(tài)角φ_di、θ_di和期望升力U_1i：

U_1i=mu²_ix+u²_iy+（u_iz+g）²

φ_di=arcsinmU_1i（u_ixsin _di-u_iycos _di）

θ_di=arccos（u_iz+g）mU_1icos φ_di（15）

由此實現(xiàn)QUAV內(nèi)外環(huán)的解耦。

位置控制回路主要通過基于卡爾曼一致性濾波的無人機集群蜂擁控制算法實現(xiàn)，無人機估計的領(lǐng)導(dǎo)者狀態(tài)將直接應(yīng)用于蜂擁控制協(xié)議中。其控制輸入主要由3部分組成：考慮信息交互距離的無人機集群的速度一致控制;基于無人機間相互作用力的無人機集群群聚與避碰控制;引入卡爾曼一致性濾波估計結(jié)果的領(lǐng)導(dǎo)者軌跡跟蹤控制。依據(jù)蜂擁控制算法可得到式（14）所示的QUAV i的虛擬控制量。

內(nèi)環(huán)姿態(tài)控制回路通過BELBIC控制器實現(xiàn)。通過式（15）進行姿態(tài)解算，得到內(nèi)環(huán)控制所需期望姿態(tài)角。建立BELBIC姿態(tài)控制器實現(xiàn)QUAV對期望姿態(tài)角的跟蹤。

綜合內(nèi)外環(huán)控制回路的輸出，得到當(dāng)前時刻各無人機的運動狀態(tài)信息，并將其反饋至輸入位置控制回路的無人機集群蜂擁控制算法，形成完整的閉環(huán)反饋控制回路，實現(xiàn)QUAV集群蜂擁控制。

3 基于卡爾曼一致性濾波的蜂擁控制算法

3.1 卡爾曼一致性濾波算法

無人機對領(lǐng)導(dǎo)者的運動狀態(tài)進行估計，并將狀態(tài)估計信息與其鄰居節(jié)點共享，引入一致性濾波器對傳感器測量值以及協(xié)方差值進行融合，從而提高整個無人機集群對領(lǐng)導(dǎo)者運動狀態(tài)的估計精度，實現(xiàn)噪聲抑制。

定理 1 考慮具有連續(xù)線性觀測模型的傳感器網(wǎng)絡(luò)如式（6）所示，每個節(jié)點應(yīng)用如下形式的卡爾曼一致性濾波器的分布式估計算法：

x^·_i=Ax^_i+K_i（z_i－H_ix^_i）+μP_i∑j∈Ni（x^_j－x^_i）

K_i=P_iHT_iR^－1_i， μgt;0

P·_i=AP_i+P_iAT+BQBT－K_iR_iKT_i（16）

式中：v^_i為傳感器i對系統(tǒng)狀態(tài)x的估計值;P_i為傳感器i先驗估計誤差的協(xié)方差;系統(tǒng)初始狀態(tài)為x^_i（0）=x（0），P_i（0）=P₀。則傳感器i的估計誤差η_i=x－v^_i是全局漸近穩(wěn)定的。

證明 設(shè)李雅普諾夫函數(shù)為

V（η）=∑ni=1ηT_iP_i^－1η_i（17）

對其求導(dǎo)，有

V·（η）≤－2μ［ηT（LI_m）η］≤0（18）

且所有傳感器節(jié)點的估計值漸近達到一致，即x^₁=x^₂=…=x^_n=x。證畢

3.2 蜂擁控制算法設(shè)計

基于無人機運動方程式（式（3））與領(lǐng)導(dǎo)者的狀態(tài)方程式（式（5）），定義蜂擁控制算法的控制輸入組成如下所示：

u_i=u_αi+u_βi+u_γi， i=1，2，…，n（19）

式中：u_αi為速度一致項;u_βi為避碰控制項;u_γi為領(lǐng)導(dǎo)者反饋項。

3.2.1 速度一致項

結(jié)合無人機集群的通信模型，考慮集群中QUAV間信息交互距離的限制。定義無人機集群速度一致項的控制輸入為

u_αi=K₁∑nj=1φ（r_ij）（p_j－p_i）（20）

式中：K₁為正常數(shù);φ（r_ij）為影響強度函數(shù)，表達式為

φ（r_ij）=1α1（1+r²_ij）^β－1（1+d²_max）^β， r_ij≤d_max

0， r_ijgt;d_max（21）

式中：r_ij=q_j－q_i為無人機i與無人機j之間的距離;α=1－1（1+d²_max）^β;βgt;0。

3.2.2 避碰控制項

考慮QUAV個體實際體積帶來的避碰需求，設(shè)置無人機間的期望間距。定義避碰控制項的控制輸入為

u_βi=K₂∑nj=1a_ijσ₁2r²_ij〈p_j－p_i，q_j－q_i〉×

（q_j－q_i）+∑nj=1a_ijσ₂2r_ij（r_ij－R₀）（q_j－q_i）（22）

式中：σ₁，σ₂為正常數(shù)比例因子;R₀為兩架無人機間的期望距離。

引理 3^［32］ 定義無人機間的相互作用力為

μ_ij=－σ₁2r_ij〈p_i－p_j，q_i－q_j〉+σ₂2（R₀－r_ij）（23）

式中：〈q，p〉=∑^d_i=1q_ip_i。將由該相互作用力作用產(chǎn)生的加速度輸入在適宜的正常數(shù)σ₁、σ₂下，將指數(shù)收斂至零。

3.2.3 領(lǐng)導(dǎo)者反饋項

設(shè)置變速度領(lǐng)導(dǎo)者對無人機集群運動軌跡加以引導(dǎo)控制，使無人機集群運動滿足任務(wù)要求。定義領(lǐng)導(dǎo)者反饋項的控制輸入為

u_γi=γ_i［u^_γ－K₃（q_i－q·_γ）－K₄（p_i－p^_γ）］（24）

式中：q·_γ，p^_γ，u^_γ分別為無人機i對領(lǐng)導(dǎo)者位置、速度和加速度的估計值;K₃、K₄均為正常數(shù);K₃為路徑跟隨比例因子;K₄為速度跟隨比例因子;γ_i表示當(dāng)前時刻無人機i能否觀測到領(lǐng)導(dǎo)者的運動狀態(tài)，即：

γ_i= q_γ－q_i≤R_max

0， q_γ－q_igt;R_max（25）

綜合式（19）、式（20）、式（22）、式（24），無人機集群蜂擁控制算法控制輸入設(shè)計為

u_i=K₁∑nj=1φ（r_ij）（p_j－p_i）+

K₂∑nj=1a_ijσ₁2r²_ij〈p_j－p_i，q_j－q_i〉（q_j－q_i）+

∑nj=1a_ijσ₂2r_ij（r_ij－R₀）（q_j－q_i）］+

γ_i［u^_i，γ－K₃（q_i－q·_γ）－K₄（p_i－p^_γ）（26）

3.3 穩(wěn)定性分析

構(gòu)造能量函數(shù)，并利用李雅普諾夫穩(wěn)定性定理對算法進行穩(wěn)定性分析。

根據(jù)勢函數(shù)與勢場力的關(guān)系，記由無人機間相互作用力產(chǎn)生的勢場為_α（r），則有

_α（r）=∫^r_ij0μ_ijdr（27）

記無人機集群通信拓撲變化的時刻為t₁，t₂，t₃，…，且其拓撲結(jié)構(gòu)在每個非空有界不重疊的時間間隔［t_l，t_l+1）（l=0，1，2，…）內(nèi)是不變的。定義系統(tǒng)的總能量Q為個體之間的總勢能及個體與領(lǐng)導(dǎo)者之間的相對勢能和動能之和，具體如下：

Q=12∑ni=1（K₂U（q_i）+γ_iK₃（q_i－q_γ）T×

（q_i－q_γ）+（p_i－p_γ）T（p_i－p_γ））（28）

U（q_i）=∑nj=1，j≠i_α（q_j－q_i）（29）

考慮卡爾曼一致性濾波算法引入的估計誤差，設(shè)置李雅普諾夫函數(shù)為

Vf=Q+k2μ（ηTP^－1η）（30）

式中：估計誤差項為η=col（η₁，η₂，…，η_n）。

假設(shè) 1 存在時間T₁gt;0，使網(wǎng)絡(luò)在t≥T₁時保持連通。

記蜂擁控制算法中的連續(xù)鄰接矩陣為Af（q）=［af_ij（q）］，其中，af_ij（q）=φ（r_ij）;其拉普拉斯矩陣和網(wǎng)絡(luò)連通度分別記為Lf與λf2=λ₂（Lf）;卡爾曼一致性濾波算法中的0-1鄰接矩陣為A_e（q），其拉普拉斯矩陣和網(wǎng)絡(luò)連通度分別記為L_e與λ^e₂=λ₂（L_e）。

假設(shè) 2 存在時間T₂gt;T₁和固定閾值ε₁，ε₂∈（0，1），使tgt;T₂時，λf2（t）≥ε₁，λe₂（t）≥ε₂。取參數(shù)0lt;K₃≤K₄lt;1，K₄gt;1－ε₁，kgt;1/ε₂。

假設(shè) 3 在狀態(tài)估計模型中，對于過程噪聲ω和v_i，取：

ω_ei=Bω+P_iHT_iR^－1_iv_i（31）

Λ=diag（HT_iR^－1_iH_i+P^－1_iBQBTP^－1_i）（32）

滿足-ηTΛη+2∑ⁱ_nωT_eiP^-1_iη_i≤0。

定理 2

考慮由n個節(jié)點組成的系統(tǒng)，每個節(jié)點的運動方程如式（3）所示，領(lǐng)導(dǎo)者的狀態(tài)方程如式（5）所示，節(jié)點上的傳感器觀測方程如式（6）所示。使用卡爾曼一致性濾波算法估計領(lǐng)導(dǎo)者的運動狀態(tài)，并將估計結(jié)果直接應(yīng)用于蜂擁控制算法（如式（26）所示）。假設(shè)初始網(wǎng)絡(luò)G（0）連通且初始時刻V_f0為有限值，則可得到以下結(jié)論：

（1） 任意QUAV和領(lǐng)導(dǎo)者之間的距離不超過2V_f0/K₃;所有無人機的速度均會漸近收斂至領(lǐng)導(dǎo)者的速度p_γ;

（2） 無人機集群中所有個體對領(lǐng)導(dǎo)者的狀態(tài)估計值會一致趨于其真實狀態(tài)，即limt→∞x^_i－x=0;

（3） 若系統(tǒng)的初始時刻V_f0lt;（k-+1）_α（0），k-∈Z₊，則至多有k-對無人機會相撞;當(dāng)k-=0時，所有無人機均不會相撞。

證明 結(jié)合式（26）和式（29），無人機的運動方程可表示為

q·_i=p_i

p·_i=－K₂Δ_qiU（q）+K₁∑j∈Niaf_ij（q）（p_j－p_i）+

γ_i［u^_i，γ－K₃（q_i－q^_i，γ）－K₄（p_i－p^_i，γ）］（33）

進而可寫為

q·_i=p_i

p·_i=－K₂Δ_qiU（q）+K₁∑j∈Niaf_ij（q）（p_j－p_i）+

γ_i［u_γ－K₃（q_i－q_γ）－K₄（p_i－p_γ）－

（u_γ－u^_i，γ）－K₃（q_γ－q^_i，γ）－K₄（p_γ－p^_i，γ）］（34）

定義矩陣C=［K₃I_m，K₄I_m，I_m］，則式（34）可寫為

q·_i=p_i

p·_i=－K₂Δ_qiU（q）+K₁∑j∈Niaf_ij（q）（p_j－p_i）+

γ_i［f^γ_i－Cη_i］（35）

式中：f^γ_i=u_γ－K₃（q_i－q_γ）－K₄（p_i－p_γ）。

記無人機個體與領(lǐng)導(dǎo)者的相對位置為q～_i=q_i－q_γ，相對速度為p～_i=p_i－p_γ，則式（35）可進一步表示為

q～·_i=p～_i

p～·_i=K₁∑j∈Niaf_ij（q～）（p～_j－p～_i）－K₂Δ_q～iU（q～_i）－

γ_i［K₃q～_i+K₄p～_i+Cη_i］（36）

能量函數(shù)Q可表示為

Q=12∑ni=1（K₂U（q～_i）+γ_iK₃q～T_iq～_i+p～T_ip～_i）（37）

對能量方程式（28）和式（29）求導(dǎo)，有

Q·=12∑ni=1［2K₂p～T_iΔ_q～iU（q～_i）+2γ_iK₃p～T_iq～_i+2p～T_ip～·_i］=

K₂p～TΔU（q～）+K₃H^fp～Tq～+p～Tp～·=

-p～T（K₄H^f+K₁L^f（q～））p～-∑i=1，2，…，nγ_ip～T_iCη_i（38）

式中：Hf=diag（γ₁，γ₂，…，γ_n）;H^f=HfI_m;L^f（q～）=Lf（q～）I_m。令c=max（K₂，K₃，1），有

|p～T_iCη_i| ≤ 12（p～_i2+c²η_i2）（39）

∑ip～T_iCη_i≤12（‖p～‖2+c²‖η‖2）（40）

結(jié)合式（28）和式（40），有

Q·≤－p～T（K₄H^f+K₁L^f（q～））p～+12（p～2+c²η2）（41）

基于式（16）所示卡爾曼一致性濾波算法，有

η·_i=（A－K_iH_i）η_i+μP_i∑j∈Ni（η_j－η_i）（42）

Δη（ηTP^－1η）=－ηTΛη－2μηTL^eη≤－2μηTL^eη（43）

依據(jù)假設(shè)1和假設(shè)2，有c=1，1－K₄－λf2lt;0，同時取kgt;1/λe₂。依據(jù)引理1，K₄H^f+K₁L^f（q～）為正定矩陣。故對李雅普諾夫函數(shù)Vf求導(dǎo)可得

V·f=Q·+k2μΔη（ηTP^－1η）≤－p～T（K₄H^f+K₁L^f（q～））p～+

12（p～2+c²η2）－2μηTL^eη≤

12－K₃－λf2p～2+c²2－kλe₂η2≤0（44）

即在任意時間間隔［t_l，t_l+1）內(nèi)，V_f0為非增函數(shù)，且對于任意無人機i有K₃q～T_iq～_i≤2V_f0，即任意無人機與領(lǐng)導(dǎo)者之間的距離不超過2V_f0/K₃。

依據(jù)引理2，集合

Ω={（q～，p～，η）|Vf（q～，p～，η）≤V_f0}（45）

是一個正不變緊集。根據(jù)LaSalle不變集原理，始于Ω內(nèi)的解均趨于最大不變集

Ω-={（q～，p～，η）|V·f（q～，p～，η）=0}（46）

由此可得p～₁=p～₂=…=p～_n=0，即p₁=p₂=…=p_n=p_γ。所有無人機的速度都可以漸近地收斂到領(lǐng)導(dǎo)者的速度。由此定理2中結(jié)論（1）得證。

此外，依據(jù)式（46），系統(tǒng)穩(wěn)定時，η2=0，因此所有無人機對領(lǐng)導(dǎo)者的狀態(tài)估計值會一致趨近于其真實狀態(tài)。由此定理2中結(jié)論（2）得證。

假設(shè)在t′gt;0時刻至少有k-+1對無人機發(fā)生碰撞，即無人機i與無人機j（i，j=1，2，…，k-+1）發(fā)生碰撞，則有

V_α（q）=12∑k，l∈Ni（t）_α（q_kl）=

∑k-+1i=1_α（q_i－q_j）+12∑k∈Ni（t）k，l≠i，j_α（q_kl）gt;

（k-+1）_α（0）（47）

又由V·f≤0，故在t′時刻有：

V_f0≥Vf（t′）gt;V_α（q）gt;（k-+1）_α（0）（48）

與假設(shè)矛盾。故最多有k-對無人機會相撞;k-=0時，所有無人機間無碰撞。由此定理2中結(jié)論（3）得證。證畢

4 基于BELBIC的QUAV姿態(tài)控制

4.1 BEL模型

BEL模型基于哺乳動物邊緣系統(tǒng)情感學(xué)習(xí)架構(gòu)建立，主要針對大腦情感機制中杏仁核和前額皮層兩部分的行為進行模擬。大腦情感的學(xué)習(xí)行為主要發(fā)生在杏仁核中，前額皮層的主要作用為抑止從杏仁核傳來的不恰當(dāng)?shù)姆磻?yīng)并對整體的情感學(xué)習(xí)進行調(diào)節(jié)，其結(jié)構(gòu)如圖2所示。

BEL模型受到的外部刺激信號主要為感官輸入信號SI及獎勵信號REW。丘腦接收感官輸入信號SI并分離出其中的最大值A(chǔ)_bth傳輸至杏仁核，即

A_bth=max（SI_i）（49）

同時，感官輸入信號SI經(jīng)由丘腦及感覺皮層傳遞至杏仁核及前額皮層中。對于每一個感官輸入信號SI_i，杏仁核中均有一節(jié)點與之對應(yīng)，節(jié)點輸出值記為A_bi;前額皮層中亦存在類似對應(yīng)關(guān)系，對應(yīng)節(jié)點輸出值記為O_i：

A_bi=SI_iV_bi（50）

A_bm+1=A_bthV_bm+1（51）

O_i=W_biSI_i（52）

式中：i=1，2，…，m，其中m為SI的維度;V_bi、W_bi分別為杏仁核與前額皮層對應(yīng)節(jié)點的權(quán)值。

BEL模型的情感學(xué)習(xí)是通過對權(quán)值Vb和Wb的動態(tài)調(diào)節(jié)實現(xiàn)的。ΔV_bi與SI_i的符號始終保持一致，即杏仁核的學(xué)習(xí)是不可逆的;ΔW_bi則無上述限制，以調(diào)整杏仁核的不恰當(dāng)反應(yīng)，其權(quán)值更新如下：

ΔV_bi=k_v［SI_imax（0，REW－∑m+1i=1A_bi）］（53）

ΔV_bm+1=k_v［A_bthmax（0，REW－∑m+1i=1A_bi）］（54）

ΔW_bi=k_w［SI_imax（0，E′b－REW）］（55）

式中：k_v，k_w為杏仁核及前額皮層權(quán)值的學(xué)習(xí)率;E′b為杏仁核不受丘腦刺激信號影響時模型的輸出：

E′b=∑m+1i=1A_bi－∑mi=1O_i－A_bthV_bm+1（56）

BEL模型的最終輸出為杏仁核各節(jié)點輸出與前額皮層核各節(jié)點輸出之差，即

Eb=∑m+1i=1A_bi－∑mi=1O_i（57）

4.2 穩(wěn)定性分析

BELBIC的內(nèi)部穩(wěn)定性取決于杏仁核網(wǎng)絡(luò)Ab和前額皮層網(wǎng)絡(luò)O的輸出^［33］。

杏仁核權(quán)值的狀態(tài)向量可表示為

Vb（k）=［V_b1（k），V_b2（k），…，V_bm（k），V_b（m+1）（k）］（58）

由式（53）可得，其狀態(tài)方程為

Vb（k+1）=Vb（k）+

k_vmax（0，REW（k）－SIT（k）Vb（k））（59）

若SI_i=0，此時杏仁核沒有學(xué)習(xí)信號輸入，權(quán)值穩(wěn)定。故需考慮SI_i中存在非零信號的情形。

定理 3 當(dāng)存在SI_i≠0時，假設(shè)系統(tǒng)滿足：

REW（k+1）－（k_vΔSIT（k）SI（k）+1）REW（k）≤

ΔSIT（k）（I－k_vSI（k）SIT（k））Vb（k）（60）

式中：ΔSI（k）=SI（k+1）－SI（k）;k_vgt;0。則式（59）具有李雅普諾夫意義下的穩(wěn)定性。

證明 若REW－∑^m+1_i=1A_bi≤0，則式（53）可表示為Vb（k+1）=Vb（k），此時系統(tǒng)是穩(wěn)定的。

若REW－∑^m+1_i=1A_bigt;0，則式（53）可表示為

Vb（k+1）=Vb（k）+k_vSI（k）（REW（k）－SIT（k）Vb（k））（61）

令李雅普諾夫函數(shù)為

L（k）=REW（k）－SIT（k）Vb（k）（62）

則有

ΔL（k+1）=L（k+1）－L（k）=REW（k+1）－REW（k）－

k_vSIT（k）SI（k）（REW（k）－SIT（k）Vb（k））－

k_vΔSIT（k）Vb（k+1）=REW（k+1）－

（k_vΔSIT（k）SI（k）+1）REW（k）－

ΔSIT（k）（I－k_vSI（k）SIT（k））Vb（k）－

k_vSIT（k）SI（k）（REW（k）－SIT（k）Vb（k））（63）

依據(jù)式（60），有

ΔL（k+1）≤－k_vSIT（k）SI（k）（REW（k）－SIT（k）Vb（k））≤0（64）

綜上，式（59）系統(tǒng)是穩(wěn)定的。證畢

前額皮層權(quán)值的狀態(tài)向量可表示為

Wb（k）=［W_b1（k），W_b2（k），…，W_bm（k）］（65）

由式（55）可得，其狀態(tài)方程可表示為

Wb（k+1）=Wb（k）+k_wSIT（k）［Ab（k）-O（k）-REW（k）］=

Gb（k）Wb（k）+Hb（k）（REW（k）-∑mi=1SI_i（k）W_bi（k））（66）

其中：

Gb（k）=1－k_wSIT₁SI₁－k_wSIT₁SI₂…－k_wSIT₁SI_m

－k_wSIT₁SI₂1－k_wSIT₁SI₂…－k_wSIT₂SI_m

－k_wSIT₁SI_m－k_wSIT₂SI_m…1－k_wSIT_mSI_m（67）

Hb（k）=－k_w［SI₁，SI₂，…，SI_m］T（68）

引理 4^［26］ 若存在至少一個感官輸入信號不為零，則Gb（k）存在如下兩個特征值：λ₁=1，λ₂=1－k_w∑^m_i=1SI²_i，其中λ₁=1為m－1重特征值。

定理 4 假設(shè)前額皮層學(xué)習(xí)權(quán)值的學(xué)習(xí)率k_w滿足：

0≤k_w≤1∑mi=1max（SIT_i（k）SI_i（k））（69）

limk→SymboleB@∑k－1i=0Φ（k，i+1）Hb（i）REW（i）－∑mi=1SI_i（i）W_bi（i）（70）

有界，其中Φ（k，m）=∏^k－m_i=1Gb（k－i），則式（66）系統(tǒng)具有李雅普諾夫意義下的穩(wěn)定性。

證明 狀態(tài)方程（66）可分解為零輸入響應(yīng)W_b0u和零狀態(tài)響應(yīng)W_b0x，分別表示為

W_b0u（k）=Φ（k，0）Wb（0）（71）

W_b0x（k）=∑k-1i=0Φ（k，i+1）Hb（i）（REW（i）-∑mi=1SI_i（i）W_bi（i））（72）

依據(jù)引理4，存在正交矩陣Ub（k），使得

Gb（k）=UTb（k）Λb（k）Ub（k）（73）

式中：

Λb（k）=diag1，1，…，1，1－k_w∑^m_i=1（SIT_i（k）SI_i（k））令李雅普諾夫函數(shù)為

L（k）=Wb（k）TWb（k）（74）

依據(jù)式（66），令REW=0，有

ΔL（k）=L（k+1）-L（k）=

（Wb（k+1）-Wb（k））T（Wb（k+1）+Wb（k））=

WTb（k）（G²b（k）-I）Wb（k）=

（Ub（k）Wb（k））T（Λ²b（k）-I）Ub（k）Wb（k）≤0（75）

因此，式（71）零輸入響應(yīng)函數(shù)有界。

又因為式（70）所示極限是有界的，故零狀態(tài)響應(yīng)式（72）有界。因此，式（66）系統(tǒng)具有李雅普諾夫意義下的穩(wěn)定性。證畢

4.3 基于BELBIC的QUAV姿態(tài)控制器

QUAV的姿態(tài)控制通過BELBIC控制器實現(xiàn)。其結(jié)構(gòu)如圖3所示。

QUAV姿態(tài)控制的輸入為式（15）解算所得的期望姿態(tài)角，輸出則為QUAV的實際姿態(tài)角。取姿態(tài)角跟蹤誤差eΘ及BELBIC控制器的輸出uΘ構(gòu)造感官輸入信號SI及獎勵信號REW，如下所示：

SI=k₁eΘ，k₂∫eΘdt（76）

REW=k₃eΘ+k₄∫eΘdt+k₅uΘ（77）

式中：k₁，k₂，k₃，k₄，k₅為權(quán)重調(diào)節(jié)參數(shù)。

將感官輸入信號SI及獎勵信號REW輸入BELBIC控制器，經(jīng)計算得到BEL模型輸出E_b，即為BELBIC控制器的輸出uΘ。將控制輸出uΘ作為姿態(tài)控制信號輸入QUAV模型，經(jīng)計算即可獲得QUAV的實際姿態(tài)角輸出。

以QUAV的俯仰角控制為例，基于BELBIC的姿態(tài)控制與基于PID控制器的姿態(tài)控制的控制結(jié)果對比如圖4所示，圖中藍色曲線為BELBIC控制器響應(yīng)，紅色曲線為PID控制器響應(yīng)。從圖中可以看出，BELBIC響應(yīng)速度較快、超調(diào)量較小、進入穩(wěn)定狀態(tài)時間較短，控制效果要明顯優(yōu)于PID控制。

5 仿真實驗

以“無人機集群遂行SEAD任務(wù)”為例，無人機集群由載機發(fā)射后，自主集結(jié)并沿設(shè)定搜索路徑巡航飛行，完成目標(biāo)任務(wù)。針對其中無人機集群協(xié)同運動過程構(gòu)建仿真實驗想定，對所提QUAV集群蜂擁控制策略進行仿真驗證。QUAV的模型參數(shù)依據(jù)文獻［34］設(shè)置。

執(zhí)行任務(wù)的子系統(tǒng)由50架同構(gòu)QUAV組成。在地面坐標(biāo)系內(nèi)，初始時刻每架QUAV隨機分布于［10，90］×［3，83］×［100，180］空間內(nèi)，速度矢量隨機分布于［－5，5］×［－5，5］×［0，5］內(nèi)。在機體坐標(biāo)系內(nèi)，初始時刻每架無人機的滾轉(zhuǎn)角及俯仰角均隨機分布于［－π/6，π/6］，偏航角隨機分布于［－π/4，π/4］，滾轉(zhuǎn)角角速率及俯仰角角速率隨機分布于［－π/6，π/6］，初始偏航角角速率隨機分布于［－π/4，π/4］。

根據(jù)初始時刻無人機集群位置分布，領(lǐng)導(dǎo)者的初始位置為（50，43，128），結(jié)合無人機集群電子對抗任務(wù)需求、基于Dubins路徑設(shè)置領(lǐng)導(dǎo)者的運動軌跡。依據(jù)文獻［27，35］所規(guī)劃的任務(wù)路徑，設(shè)置領(lǐng)導(dǎo)者的運動方程為

q_γx=60sinπ120（t－90）+135

q_γy=60cosπ120（t－90）+128

q_γz=0.5t+128（78）

領(lǐng)導(dǎo)者的狀態(tài)方程如式（5）所示，狀態(tài)向量為x=［q_γx，q_γy，q_γz，p_γx，p_γy，p_γz，u_γx，u_γy，u_γz］T。狀態(tài)轉(zhuǎn)移矩陣A為

A=I₃t_sI₃t²_sI₃/2

0I₃t_sI₃

00I₃（79）

矩陣B=［t⁴_sI₃/4，t²_sI₃/2，I₃］T，過程噪聲協(xié)方差矩陣Q=I₃，觀測矩陣H=［I₃，0，0］，觀測噪聲協(xié)方差矩陣R_i=0.5I₃，初始估計誤差協(xié)方差矩陣P₀=20I₉。

常數(shù)參數(shù)分別設(shè)置如下：K₁=7.5，K₂=5，K₃=0.75，K₄=0.75，σ₁=1.5，σ₂=0.8，β=0.3，ε=1.0，d_max=60，R_max=60，R₀=15。

由于BELBIC控制器在相同參數(shù)下的控制效果因姿態(tài)角跟蹤誤差e_Θi（i=1，2，3）的初始值不同而有較大差異，故依據(jù)姿態(tài)角跟蹤誤差e_Θi的大小，選取如下兩組控制參數(shù)進行姿態(tài)控制：當(dāng)|e_Θi|lt;0.2時，取k₁=156.25，k₂=15.75，k₃=17.5，k₄=0.75，k₅=0.25;當(dāng)|e_Θi|≥0.2時，取k₁=33.15，k₂=1.75，k₃=3.85，k₄=0.75，k₅=0.25。杏仁核及前額皮層權(quán)值的學(xué)習(xí)率分別取k_v=0.002 5，k_w=0.015。

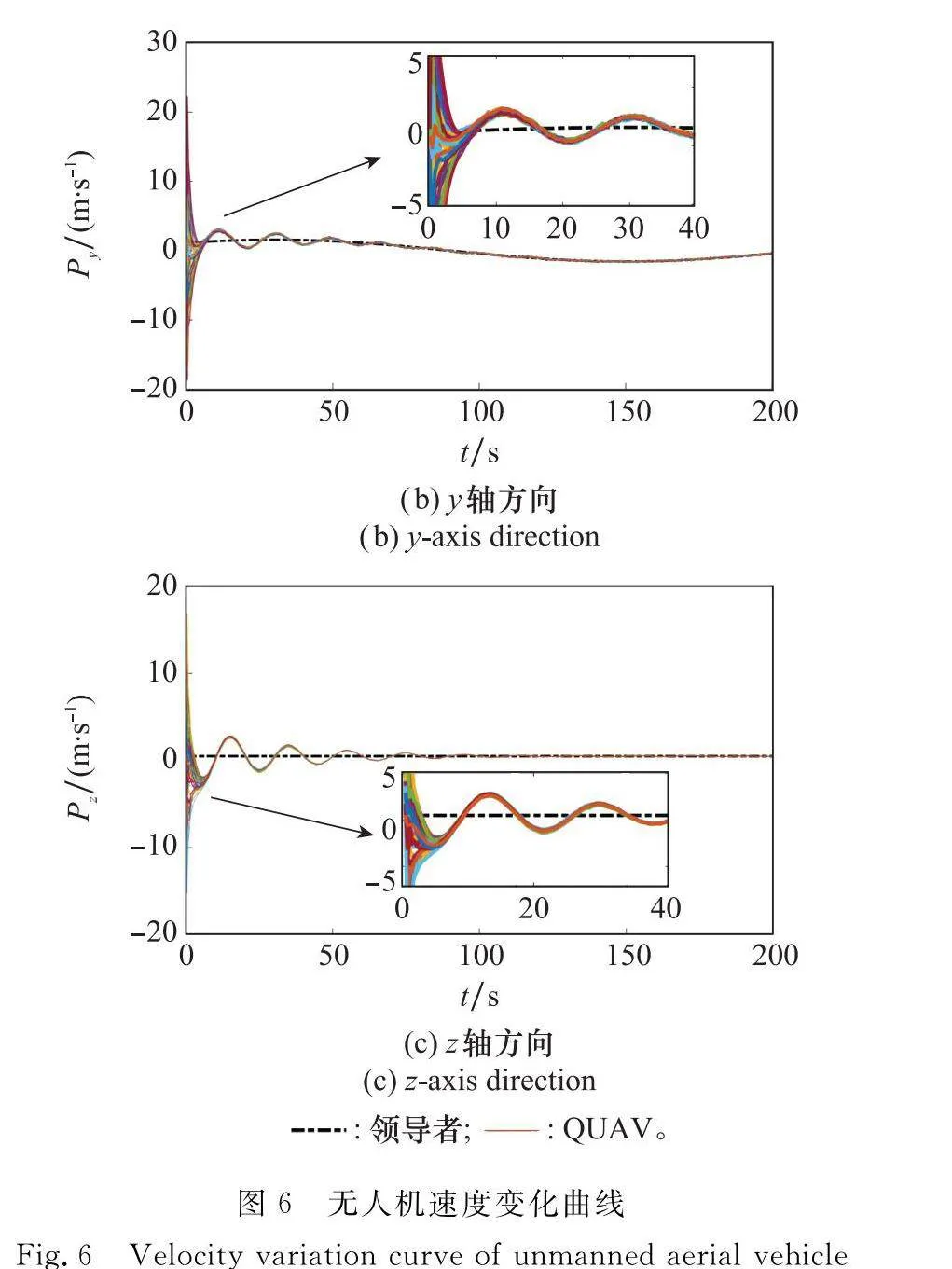
設(shè)置仿真時長t=200 s，QUAV集群在所提蜂擁控制策略下的三維運動軌跡如圖5所示，集群中各無人機的速度變化曲線如圖6所示。

由仿真結(jié)果可知，本文所建立的QUAV集群蜂擁控制策略能夠使無人機集群中初始時刻分散的無人機逐漸聚集，實現(xiàn)動態(tài)拓撲下無嚴(yán)格構(gòu)型約束的可擴展無人機集群協(xié)同運動，運動過程中無人機之間無碰撞。各無人機在各坐標(biāo)軸方向上的速度迅速收斂，并在約t=10 s時達到并保持速度矢量一致狀態(tài)，很好地契合了蜂擁模型的3條基本運動規(guī)則，控制系統(tǒng)快速收斂。

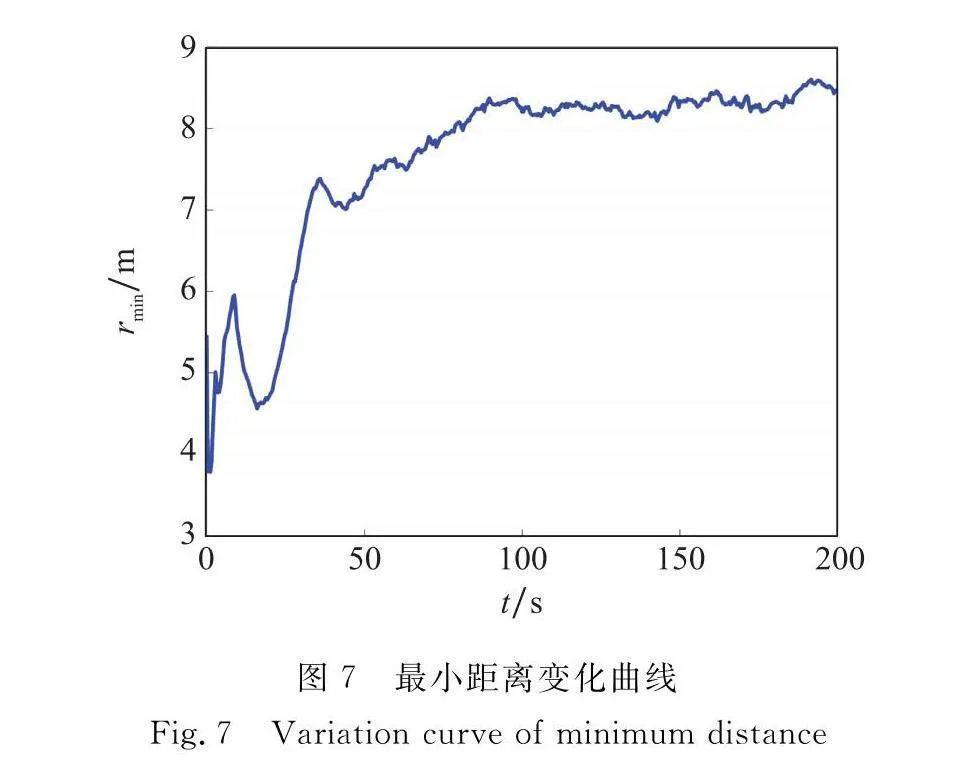
集群中無人機之間最小距離的變化曲線如圖7所示。無人機間最小距離始終大于0，無人機之間無碰撞。

當(dāng)無人機集群中僅存在兩架無人機相互作用時，無人機之間相互作用的斥力及引力會使無人機間的距離收斂至期望距離R₀=15 m，但當(dāng)集群中無人機多于兩架時則不會收斂。多架無人機之間復(fù)雜的相互作用導(dǎo)致了最終的平衡狀態(tài)，在這種平衡態(tài)中，無人機之間的最小距離略小于期望距離。

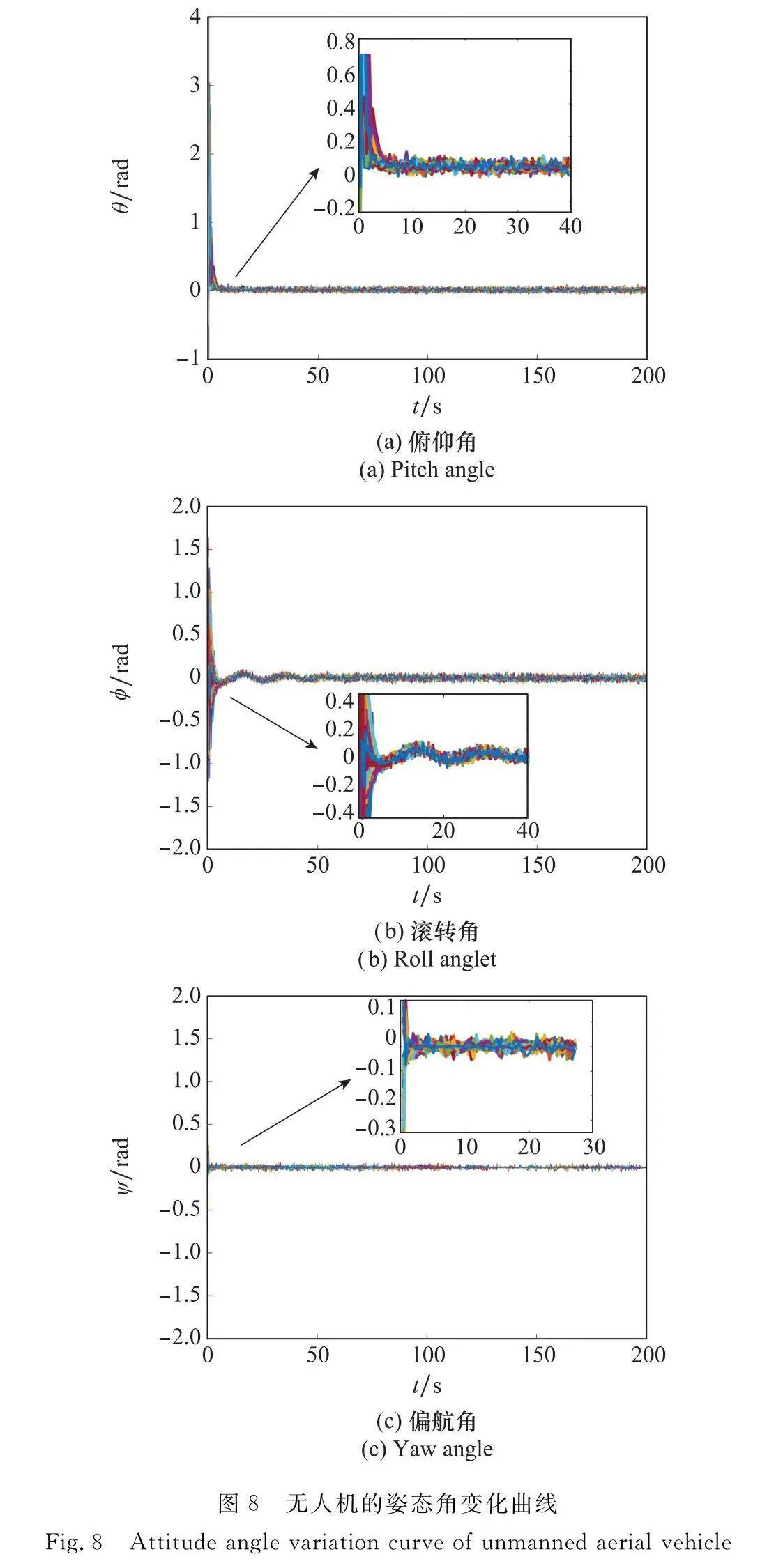
集群中各無人機的姿態(tài)角變化曲線如圖8所示。在無人機集群蜂擁控制下，QUAV的姿態(tài)角逐漸收斂并趨于同步。

綜上所述，本文所提動態(tài)拓撲下QUAV集群蜂擁控制策略能夠?qū)崿F(xiàn)無嚴(yán)格構(gòu)型約束的可擴展QUAV集群協(xié)同運動。

6 結(jié) 論

本文針對無嚴(yán)格構(gòu)型約束的無人機集群協(xié)同控制問題，面向無人機集群遂行SEAD任務(wù)，研究QUAV集群蜂擁控制問題。首先，基于QUAV的雙環(huán)控制結(jié)構(gòu)設(shè)計無人機集群蜂擁控制策略。隨后，設(shè)計基于卡爾曼一致性濾波的無人機集群蜂擁控制算法。利用卡爾曼一致性濾波算法實現(xiàn)對噪聲環(huán)境中變速度領(lǐng)導(dǎo)者狀態(tài)的估計，同時將估計結(jié)果應(yīng)用于蜂擁控制算法，實現(xiàn)位置控制回路無嚴(yán)格構(gòu)型約束的可擴展無人機集群協(xié)同控制。最后，通過BELBIC控制器實現(xiàn)QUAV姿態(tài)控制。數(shù)值仿真實驗結(jié)果表明，本文提出的無人機集群蜂擁控制策略能夠較好地實現(xiàn)無嚴(yán)格構(gòu)型約束的無人機集群協(xié)同控制，且算法具有良好的可擴展性。未來，為實現(xiàn)面向任務(wù)的無人機多模集群構(gòu)型敏捷自適應(yīng)重構(gòu)，需進一步研究考慮層級交互機制的無人機集群分群蜂擁控制問題。

參考文獻

［1］ LI R， MA H Z. Research on UAV swarm cooperative reconnaissance and combat technology［C］∥Proc.of the IEEE 3rd International Conference on Unmanned Systems， 2020： 996999.

［2］ 齊小剛， 周雨桐， 劉立芳. 無人機集群對地作戰(zhàn)任務(wù)可靠性評估［J］. 系統(tǒng)工程與電子技術(shù)， 2023， 45（9）： 29712978.

Ql X G， ZHOU Y T， LIU L F. Evaluation of the reliability of UAV swarm for ground combat missions［J］. Systems Engineering and Electronics， 2023， 45（9）： 29712978.

［3］ 陸曉安， 浦黃忠， 甄子洋， 等. 基于改進一致性算法的無人機集群飽和攻擊［J］. 電光與控制， 202 28（8）： 3135.

LU X A， PU H Z， ZHEN Z Y， et al. Saturation attack of UAV swarm based on improved consensus algorithm［J］. Electronics Optics amp; Control， 202 28（8）： 3135.

［4］ 馮政， 吳傲， 王謙喆. 無人機集群打擊海面目標(biāo)指定時間協(xié)同控制方法［J］. 電光與控制， 202 29（9）： 4347.

FENG Z， WU A， WANG Q Z. Cooperative control method of designated time for UAV swarm attacking sea target［J］. Electronics Optics amp; Control， 202 29（9）： 4347.

［5］ 張毅， 于浩， 楊秀霞， 等. 無人機集群分組編隊控制跟蹤一體化設(shè)計［J］. 系統(tǒng)工程與電子技術(shù)， 2023， 45（3）： 848858.

ZHANG Y， YU H， YANG X X， et al. Integrated design of group formation control and tracking of UAV swarm［J］. Systems Engineering and Electronics， 2023， 45（3）： 848858.

［6］ REYNOLDS C W. Flocks， herds， and schools： a distributed behavioral model［J］. Computer Graphics， 1987， 21（4）： 2534.

［7］ VICSEK T， CZIROK A， BEN-JACOB E， et al. Novel type of phase transition in a system of self-driven particles［J］. Physical Review Letters， 1995， 75（6）： 12261229.

［8］ CUCKER F， SMALE S. Emergent behavior in flocks［J］. IEEE Trans.on Automatic Control， 2007， 52（5）： 852862.

［9］ OLFATI-SABER R. Flocking for multi-agent dynamic systems： algorithms and theory［J］. IEEE Trans.on Automatic Control， 2006， 51（3）： 401420.

［10］ GAO J Y， XU X， DING N， et al. Flocking motion of multi-agent system by dynamic pinning control［J］. IET Control Theory amp; Applications， 2017， 11（5）： 714722.

［11］ YAN T， XU X， LI Z， et al. Flocking of multi-agent system with dynamic topology by pinning control［J］. IET Control Theory amp; Applications， 2020， 14（20）： 33743381.

［12］ LIANG Z L， LIU X Z. Hybrid event-triggered impulsive flock-ing control for multi-agent systems via pinning mechanism［J］. Applied Mathematical Modelling， 2023， 114： 2343.

［13］ IZADIPOUR A， GHAISARI J， ASKARI J. Distributed robust adaptive flocking for uncertain nonlinear multi-agent systems with time-varying communication delay［J］. International Journal of Systems Science， 2020， 51（1）： 7286.

［14］ OLFATI-SABER R， JALALKAMALI P. Coupled distributed estimation and control for mobile sensor networks［J］. IEEE Trans.on Automatic Control， 201 57（10）： 26092614.

［15］ SU H， CHEN X， CHEN M Z Q， et al. Distributed estimation and control for mobile sensor networks with coupling delays［J］. ISA Transactions， 2016， 64： 141150.

［16］ LUO X Y， LI X L， LI S B， et al. Flocking for multi-agent systems with optimally rigid topology based on information weighted Kalman consensus filter［J］. International Journal of Control， Automation and Systems， 2017， 15（1）： 138148.

［17］ ZHANG L L， DONG X X， YAO L X， et al. Velocity-varying target tracking of mobile sensor network based on flocking control［J］. Journal of Shanghai Jiaotong University （Science）， 202 26（4）： 446453.

［18］ LIU X Y， XIANG X J， CHANG Y， et al. Hierarchical weighting Vicsek model for flocking navigation of drones［J］. Drones， 202 5（3）： 74.

［19］ QIU H X， DUAN H B. A multi-objective pigeon-inspired optimization approach to UAV distributed flocking among obstacles［J］. Information Sciences， 2020， 509： 515529.

［20］ HUANG F J， WU P L， LI X X. Distributed flocking control of quadrotor UAVs with obstacle avoidance under the parallel-triggered scheme［J］. International Journal of Control， Automation and Systems， 202 19（3）： 13751383.

［21］ YAN D H， ZHANG W G， CHEN H， et al. Robust control strategy for multi-UAVs system using MPC combined with Kalman-consensus filter and disturbance observer［J］. ISA Transactions， 2023， 135： 3551.

［22］ ARRIETA O， CAMPOS D， RICO-AZAGRA J， et al. Model-based optimization approach for PID control of pitch-roll UAV orientation［J］. Mathematics， 2023， 11（15）： 3390.

［23］ LIU N， SHAO X L， LI J， et al. Attitude restricted back-stepping anti-disturbance control for vision based quadrotors with visibility constraint［J］. ISA Transactions， 2020， 100： 109125.

［24］ MARTINEZ-VASQUEZ A H， CASTRO-LINARES R， RODRGUEZ-MATA A E， et al. Spherical inverted pendulum on a quadrotor UAV： a flatness and discontinuous extended state observer approach［J］. Machines， 2023， 11（6）： 578.

［25］ HU M Y， LEE K， AHN H， et al. Stabilization and tracking of a quadrotor using modified sigmoid sliding mode control［J］. Sensors， 202 22（10）： 3618.

［26］ 黃國勇. 變推力軸線無人機飛行控制技術(shù)研究［D］. 南京： 南京航空航天大學(xué)， 2009.

HUANG G Y. Research on flight control technology of variable thrust axis UAV［D］. Nanjing： Nanjing University of Aeronautics and Astronautics， 2009.

［27］ WANG H， SHAN J J. Fully distributed event-triggered formation control for multiple quadrotors［J］. IEEE Trans.on Industrial Electronics， 2023， 70（12）： 1256612575.

［28］ 鄒立巖， 張明智， 柏俊汝. OODA-L模式下的智能無人集群作戰(zhàn)仿真建模框架［J］. 國防科技大學(xué)學(xué)報， 202 43（4）： 163170.

ZOU L Y， ZHANG M Z， BAI J R. Modeling framework for intelligent unmanned swarm operation simulation under OODA-L pattern［J］. Journal of National University of Defense Technology， 202 43（4）： 163170.

［29］ YE F， CHEN J， TIAN Y， et al. Cooperative task assignment of a heterogeneous multi-UAV system using an adaptive genetic algorithm［J］. Electronics， 2020， 9（4）： 687.

［30］ HONG Y G， HU H P， GAO L X. Tracking control for multi-agent consensus with an active leader and variable topology［J］. Automatica， 2006， 42（7）： 11771182.

［31］ KHALIL H K. Nonlinear systems［M］. New Jersey： Prentice Hall， 2002： 126129.

［32］ AHN S M， CHOI H， HA S Y， et al. On collision-avoiding initial configurations to Cucker-Smale type flocking models［J］. Communications in Mathematical Sciences， 201 10（2）： 625643.

［33］ YEGANEH M S O， OSHNOEI A， MIJA-TOVIC N， et al. Intelligent secondary control of islanded AC microgrids： a brain emotional learning-based approach［J］. IEEE Trans.on Industrial Electronics， 2023， 70（7）： 67116723.

［34］ HEO J， CHWA D. Robust tracking control using integral sliding mode observer for quadrotors considering motor and propeller dynamics and disturbances［J］. Journal of Electrical Engineering amp; Technology， 202 16（6）： 32473260.

［35］ VNˇA P， FAIGL J. Optimal solution of the generalized Dubins interval problem： finding the shortest curvature-constrained path through a set of regions［J］. Autonomous Robots， 2020， 44（7）： 13591376.

作者簡介

殷雅萱（1999—），女，碩士研究生，主要研究方向為無人機集群協(xié)同控制。

張 安（1962—），男，教授，博士，主要研究方向為航空武器火力控制技術(shù)。

畢文豪（1986—），男，副研究員，博士，主要研究方向為火力指揮與控制。

楊 盼（1996—），女，博士研究生，主要研究方向為多智能體協(xié)同控制。

黃湛鈞（1989—），男，副教授，博士，主要研究方向為機電系統(tǒng)、航電系統(tǒng)。