天基ISAR對空間軌道目標高分辨率成像問題分析

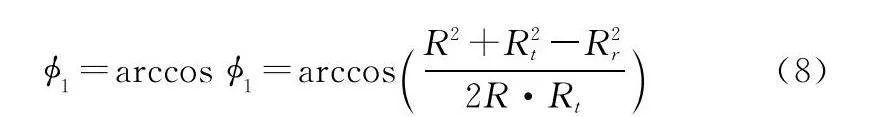
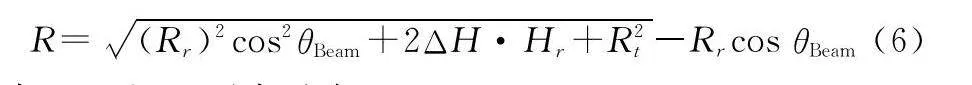
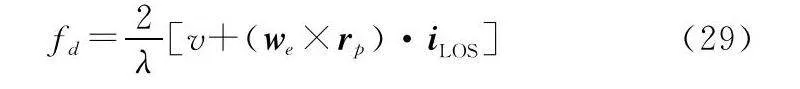
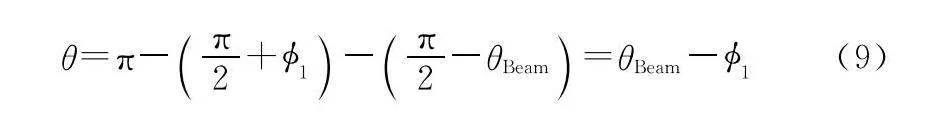
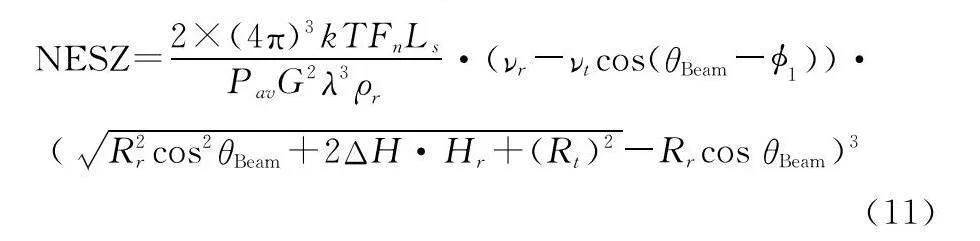
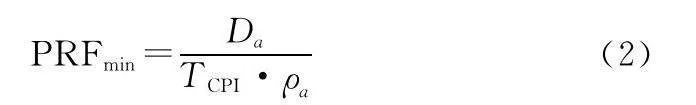
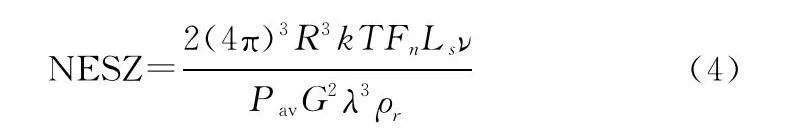
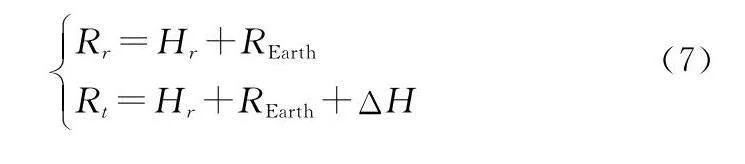
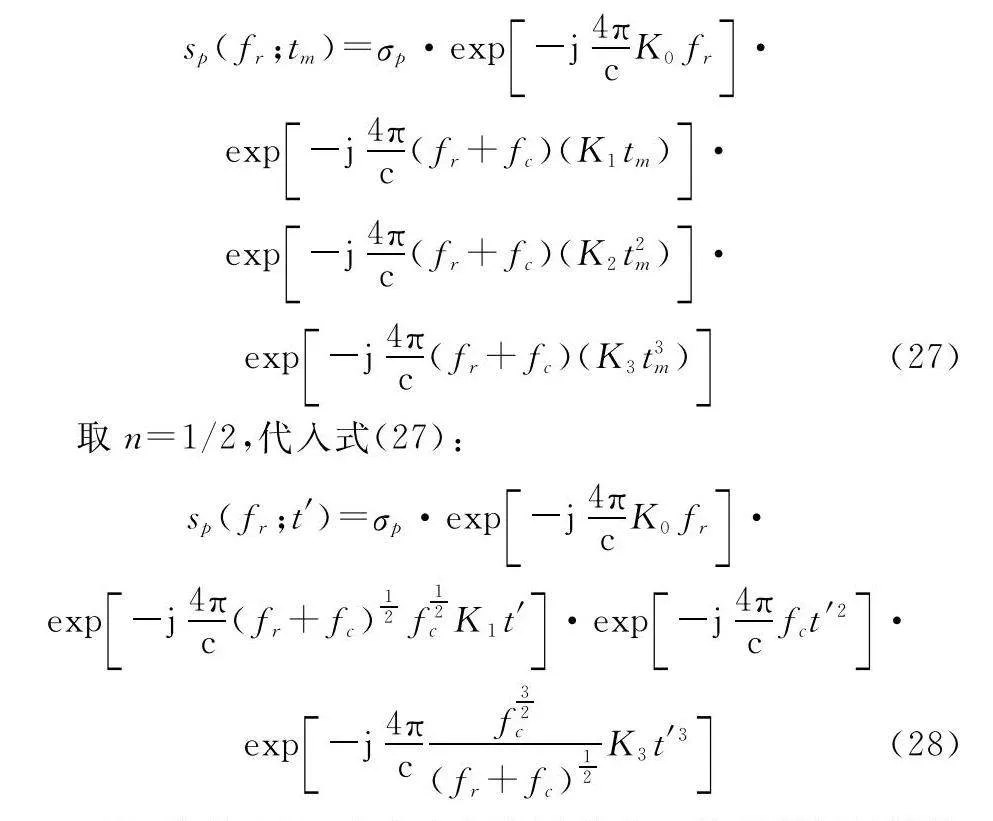
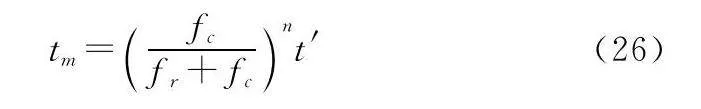
摘要： 對空間軌道目標高分辨率成像是空間態勢感知計劃的重要組成部分。本文討論天基逆合成孔徑雷達（inverse synthetic aperture radar， ISAR）對空間目標進行高分辨率成像的概念。基于雷達和空間軌道目標相對運動場景，研究減少天基ISAR回波數據量的方法;分析天基ISAR對空間目標可成像時間段的限制因素，推導天基ISAR與目標軌道高度差及天基ISAR波束掃描角度的噪聲等效后向散射系數（noise equivalent sigma zero， NESZ）公式，探討滿足方位分辨率的天基ISAR在軌可成像時間段，并利用NESZ衡量可成像時刻內回波信噪比（signal to noise ratio， SNR），為天基ISAR系統設計提供依據。此外，還推導天基ISAR對空間軌道目標回波表達式，并研究二維圖像散焦原因，提出ISAR圖像二維相位誤差具體補償模型，通過仿真結果驗證了分析的正確性。

關鍵詞： 天基逆合成孔徑雷達; 空間軌道目標; 高分辨率成像

中圖分類號： TN 958

文獻標志碼： A

DOI：10.12305/j.issn.1001-506X.2024.11.09

Analysis of high resolution imaging for space orbit targets by space-borne ISAR

LIU Yifei^1，2， YU Weidong^1，*， YANG Shenghui^1，2， LI Shiqiang¹

（1. Aerospace Information Research Institute， Chinese Academy of Sciences， Beijing 100190， China; 2. School of Electronic， Electrical and Communication Engineering， University of Chinese Academy of Sciences， Beijing 100039， China）

Abstract： Achieving high-resolution imaging of space orbit targets， which constitutes a crucial component of space situational awareness programs. The concept of space-borne inverse synthetic aperture radar （ISAR） for achieving high-resolution imaging of space targets is discussed in this paper. Methods to reduce the amount of space-borne ISAR echo data are studied based on the relative motion between radar and space orbit targets. The limiting factors affecting the imaging time period of space-borne ISAR on space targets are analyed， and formulas for noise equivalent sigma zero （NESZ） are derived considering the height difference between the target’s orbit and the scanning angle of space-borne ISAR beams. The study explores the achievable imaging time window for azimuth resolution by using NESZ to measure the signal to noise ratio （SNR） of the echoes within the imaging time window， thereby providing guidance for the design of space-borne ISAR systems. Furthermore， this paper derives the expression of the echoes from space orbit targets for space-borne ISAR and investigates the causes of two-dimensional image defocusing. A specific compensation model for the two-dimensional phase error in ISAR images is proposed， and the correctness of the analysis is verified through simulation results.

Keywords： space-borne inverse synthetic aperture radar （ISAR）; space orbit target; high resolution imaging

0 引 言

隨著航天技術的飛速發展，各國對太空資源探索活動日益頻繁，太空已成為國家級競爭和戰略對抗的關鍵領域。空間態勢感知（space situation awareness， SSA）對在軌衛星的安全至關重要。SSA對空間中的人造物體進行監視和跟蹤，如現役和非現役衛星、圍繞軌道的空間碎片等，以此來保護衛星，防止衛星受碎片擴散造成的無意威脅和敵對衛星、導彈等物體產生的蓄意威脅^［1］。此外，還需要監測航天器在軌運行狀態及外形變化以免產生嚴重故障。因此，需要對空間在軌目標高精度成像，各航天大國都在研發可用于空間探測的高精度光學、雷達設備^［2］。

當前，空間在軌目標的雷達成像觀測主要依賴地基逆合成孔徑雷達（inverse synthetic aperture radar， ISAR） 的跟蹤監測，地基ISAR對空間目標成像已有大量研究^［3-6］。然而，地基ISAR受軌道可視弧段限制，一天內僅有固定時刻可對目標進行高精度成像;且地基ISAR成像過程中地球大氣層對雷達發射和接收信號產生嚴重衰減，并且隨著作用距離增大，回波信噪比（signal to noise ratio， SNR）急劇下降^［7］。天基ISAR以航天器為載體，通過設計航天器軌道使得ISAR對空間在軌目標近距離成像。因此，使用天基ISAR對空間軌道目標進行成像觀測可有效避免回波SNR問題，相關研究已有學者開展^［8-10］，但相關研究資料較少。文獻［11］針對空間目標的星載干涉ISAR三維成像提出一種基于星載平臺的L形正交觀測規則，利用子帶雙頻共軛處理手段解決干涉相位纏繞問題，進行空間目標三維成像。文獻［12-13］提出基于“清潔”算法的線性調頻信號估計方法，利用“高分三號”衛星所提供數據，得到天宮一號的ISAR成像結果^［14］。文獻［8］提出基于拋物線檢測和最小熵的參數化最小熵平動補償方法，實現對空間站的二維成像。

天基ISAR工作模式決定了成像場景，為避免地球表面陸地及海洋的雜波干擾，ISAR軌道應低于目標軌道，雷達波束指向軌道上方。天基ISAR在軌運行時存在兩種基礎成像模式：巡視模式和跟蹤模式。本文研究天基ISAR在跟蹤模式下對空間軌道目標高分辨率成像問題。首先基于天基ISAR的任務需求，分析天基ISAR的系統參數，對天基ISAR的成像場景進行初步假設;推導跟蹤模式下天基ISAR在與目標不同軌道高度差及波束掃描范圍下的噪聲等效后向散射系數（noise equivalent sigma zero， NESZ）^［15］一般形式，依據天基ISAR與空間目標軌道幾何關系，研究滿足方位分辨率要求的ISAR在軌可成像時刻，利用推導出的NESZ方程衡量可成像時刻下ISAR回波SNR。此外，依據可成像時刻，以衛星點散射模型給出跟蹤模式下天基ISAR對不同軌道高度目標的距離多普勒（range-Doppler， RD）高分辨率成像結果，結合目標與天基ISAR在軌道的相對運動，給出距離向和方位向待補償相位誤差具體模型。

本文組織結構如下：第1節結合天基ISAR的成像需求，對天基ISAR的系統參數進行分析討論，假定天基ISAR對在軌目標成像前提，并對高分辨率成像條件下減少天基ISAR回波數據的方式進行了討論，給出了解決方案;第2節推導不同軌道高度差、波束掃描范圍及跟蹤模式下天基ISAR NESZ表達式，依據天基ISAR與空間軌道目標相對運動確定滿足分辨率的可成像時間并使用NESZ方程衡量其SNR;第3節推導天基ISAR回波模型并依據第2節可成像時間給出對目標成像結果，驗證了可成像時間選取正確性;第4節研究圖像二維散焦原因，并對在軌目標相對于天基ISAR的合作/非合作性質進行了分析;第5節對本文進行總結。

1 天基ISAR系統參數選取

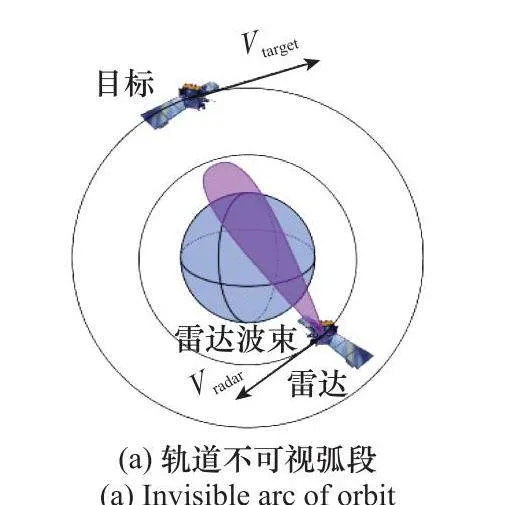
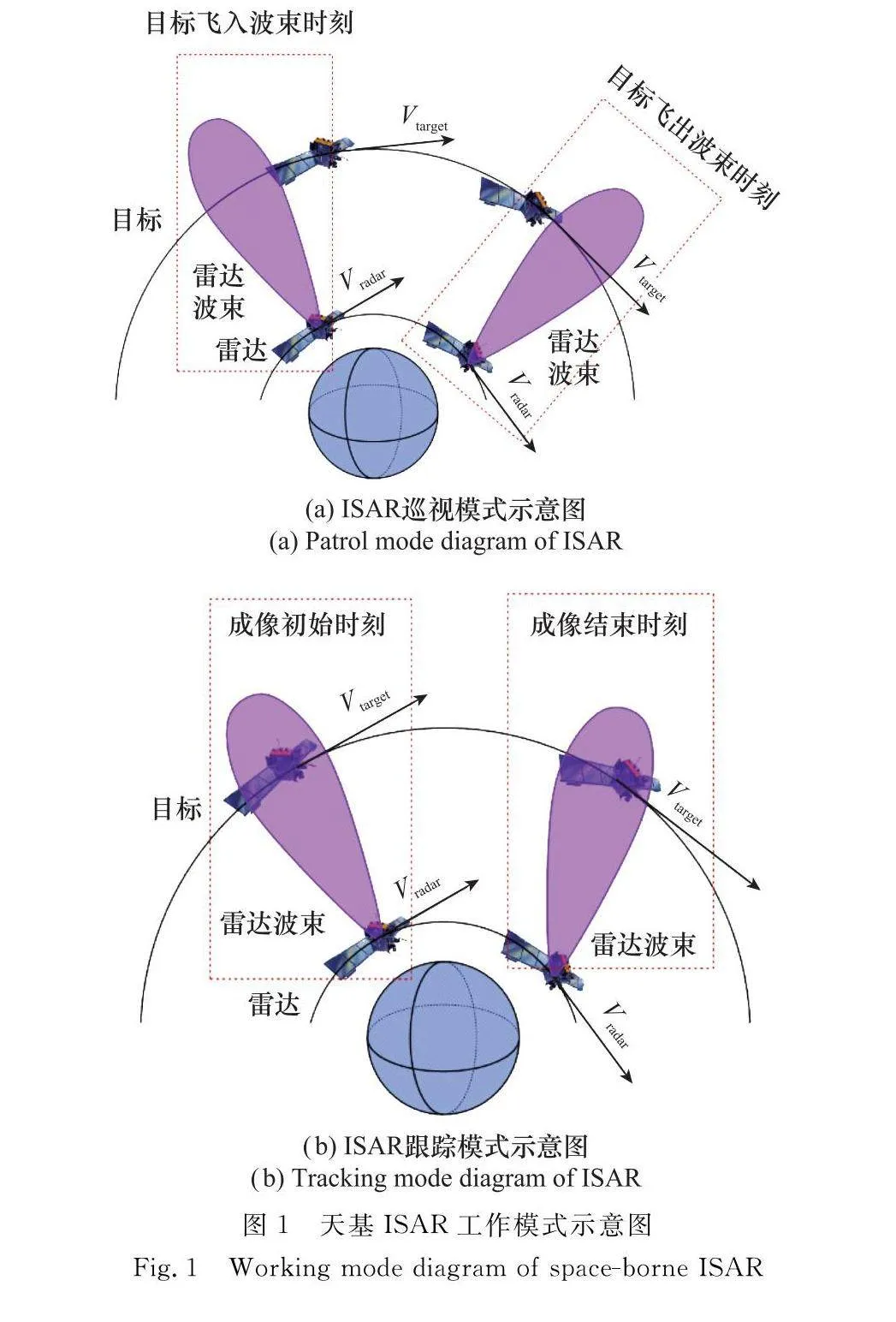
在巡視模式下，ISAR波束以固定角度照射軌道上空，如圖1（a）所示，主要任務為觀測軌道上空是否存在目標。該模式下，ISAR對在軌目標的可用觀測時間起始于目標進入ISAR波束時刻，終止于目標飛出雷達波束時刻。此時，ISAR對目標最大的成像有效旋轉角度對應于天線的波束寬度。ISAR工作在巡視模式發現目標后，將工作模式切換為跟蹤模式，如圖1（b）所示，控制波束持續指向目標進行實時跟蹤，利用目標在ISAR波束內的有效旋轉角度來獲取方位向的高分辨率。該模式下，ISAR對目標的成像有效旋轉角度對應于目標速度與ISAR視線（line of sight， LOS）夾角的變化量。對在軌目標的高分辨率成像主要在跟蹤模式下實現。

假定跟蹤模式下，天基ISAR可以在波束掃描范圍內持續跟蹤目標。ISAR方位分辨率可表示為

ρ_a=λ2Δθ（1）

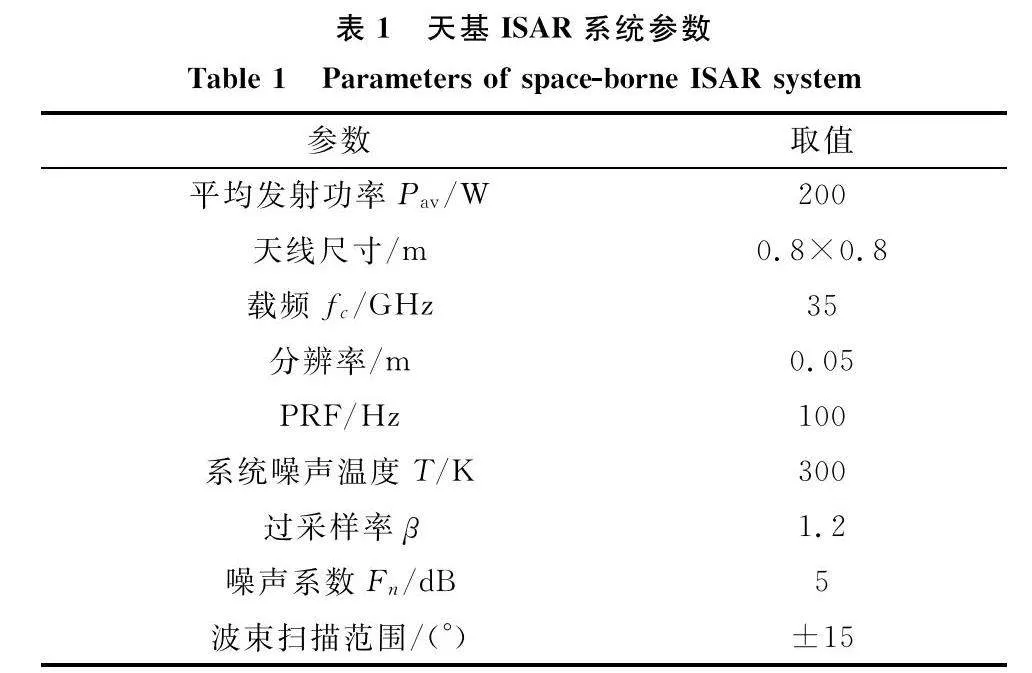
式中：λ和Δθ分別為發射信號波長及在相干處理間隔（coherent processing intervals， CPI）內目標相對天基ISAR的有效旋轉角度，等效為目標速度與ISAR LOS夾角的變化量。空間軌道目標主要為衛星、航天器等，以歐空局典型航天器Sentinel-3為例，其尺寸大小為3 710 mm×2 202 mm×2 207 mm。為獲取該類目標的重要特征，將天基ISAR二維分辨率設置為5 cm，發射信號帶寬為3 GHz。當ISAR工作在跟蹤模式時，在現有L波段、C波段和X波段天基雷達系統參數下，難以發射上述帶寬的信號。此外，依據式（1），天基ISAR發射信號波長越小，高分辨率成像所需的Δθ越小，因此選取Ka波段，中心頻率為35 GHz作為天基ISAR的載頻，此時Δθ為6°。在Ka波段下，天線尺寸更小，波束寬度更窄，有助于保證波束覆蓋范圍內只有單一目標，天基ISAR系統參數如表1所示。

近圓軌道衛星軌道高度為300～1 500 km^［16］，且多數衛星集中于780 km左右的高度^［1］。地球同步軌道衛星主要集中于36 000 km高度。天基ISAR對在軌目標成像時，首先位于巡視模式，搜索固定區域。待檢測到目標后，漂移至目標附近，對其近距離成像。近距離成像這一特點可以降低天基ISAR的系統功率，為天基ISAR的小型化提供了保障。天基ISAR對在軌目標成像時，二者的運行軌道不可避免地會出現軌道相對傾角差，較大的軌道相對傾角差會使得在軌目標相對天基ISAR的斜距變化劇烈，增大天基ISAR的脈沖重復頻率（pulse repetition frequency， PRF）需求，使得回波數據量增大。對于低功率ISAR系統來說，在軌目標可能會在短時間內駛出雷達最大作用距離。此外，雷達頻段越高，天線的波束掃描范圍越小，軌道相對傾角差較大時，在軌目標也可能會短時間駛出天基ISAR的觀測范圍。特別對地球同步軌道目標來說，由于軌道高度較高，即便是較小的軌道相對傾角差，也會導致上述問題。因此，天基ISAR對在軌目標成像時，二者的軌道相對傾角差應盡可能小。此外，天基ISAR發現目標后，由于Ka波段天線波束寬度較窄，漂移至目標附近時也可保證自身與在軌目標軌道相對傾角差較小，因此假定天基ISAR與在軌目標軌道相對傾角差小于2°，當對地球同步軌道目標成像時，應盡可能小于1°。此外，天基ISAR和在軌目標沿軌道運動時，在CPI內假定天基ISAR平臺和在軌目標運動軌跡為圓弧。

由于受到軌道動力學的約束，天基ISAR與在軌目標相對運動緩慢，即便在Ka波段下也會產生大量觀測數據。距離向數據量主要取決于天基ISAR發射信號帶寬和成像幅寬。方位向回波數據主要取決于CPI和天基ISAR的PRF。在高分辨率前提下，回波距離向的數據量遠遠大于方位向數據量。由于在軌目標主要為衛星、空間站等目標，其實際尺寸遠小于天基ISAR成像幅寬。為減小天基ISAR回波數據量，采用變采樣起始方法接收回波：將CPI分解為多個子孔徑，每個子孔徑的成像幅寬遠小于總成像幅寬，并在對回波進行距離壓縮后，設置合理能量門限ε，將每個距離單元內的信號與能量門限值ε進行比較，僅保留大于該門限距離單元內的信號，可以有效減少距離向的回波數據量。

在對天基ISAR系統的PRF進行設計時，其下限滿足^［17］：

式中：T_CPI為整個相干累計間隔；D_a為場景寬度，表示采用變采樣起始技術時，D_a每個方位子孔徑對應的成像幅寬。由于每個方位向子孔徑所對應的幅寬遠小于總成像幅寬，而CPI較大，因此實際天基ISAR系統的PRF較低，可以同時有效降低天基ISAR對在軌目標成像時回波的二維數據量。

在實際成像場景中，采用變采樣起始技術需要估計在軌目標的運動參數來預測成像總幅寬，從而確定方位子孔徑長度和每個子孔徑內的成像幅寬。天基ISAR與在軌目標的斜距可以粗略測量如下：

式中：τ和c分別為回波時延及光速。此外，可以通過卡爾曼濾波^［18］實現對在軌目標的距離跟蹤，獲取在軌目標相對天基ISAR運動參數的估計值，輔助天基ISAR回波獲取過程中的方位向子孔徑大小設置。

2 可成像時刻及其NESZ

2.1 可成像時間段分析

巡視模式下，天基ISAR最大方位分辨率取決于天線波束寬度，空間目標駛入及駛出天線波束時刻計算方法可參考文獻［1］。因此，本節重點關注跟蹤模式下滿足方位分辨率要求的天基ISAR在軌可成像時間段及其SNR。然而，受軌道不可視弧段、雷達波束掃描范圍限制，在天基ISAR與空間軌道目標相對周期性運動過程中，并非所有時刻均可成像。

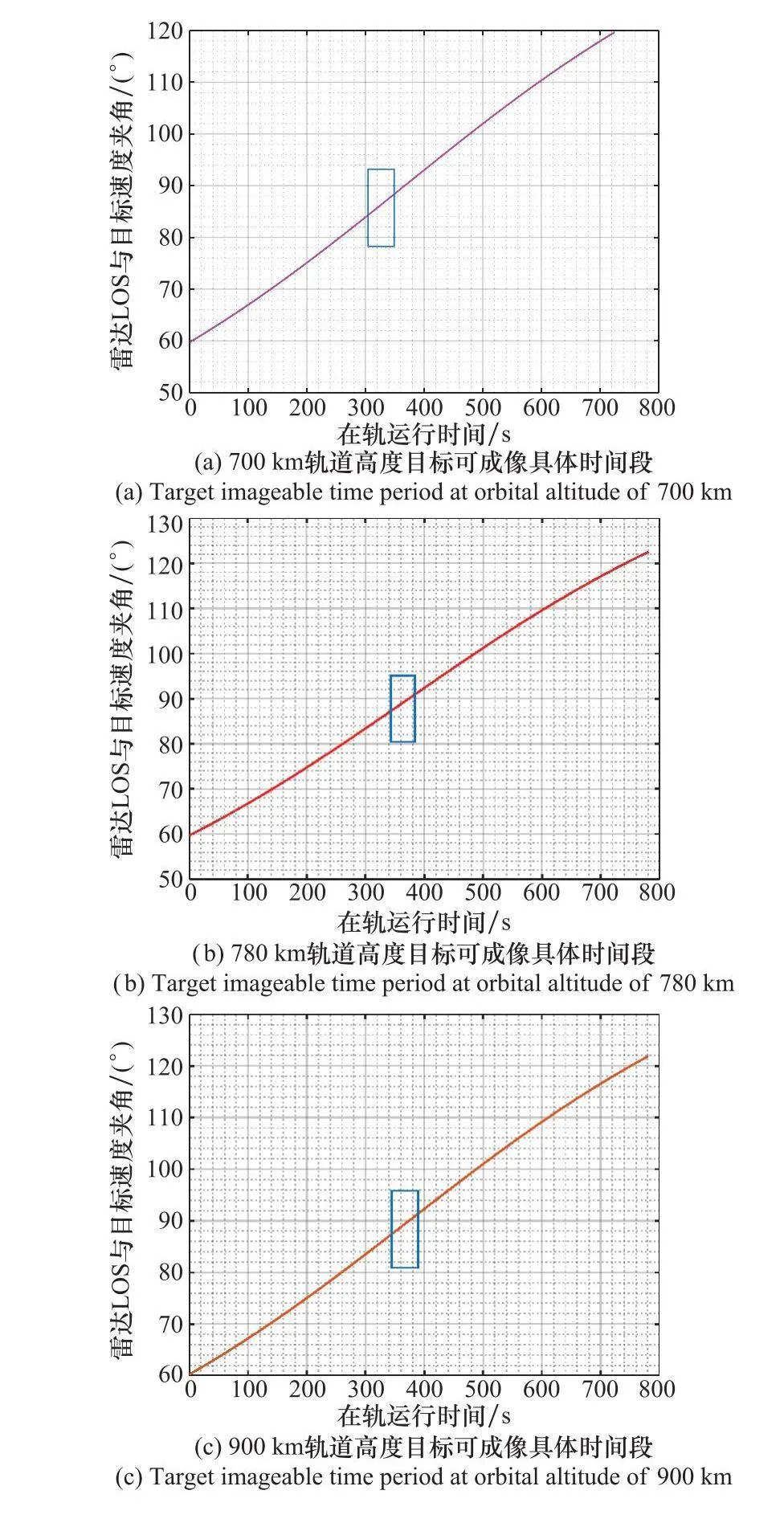
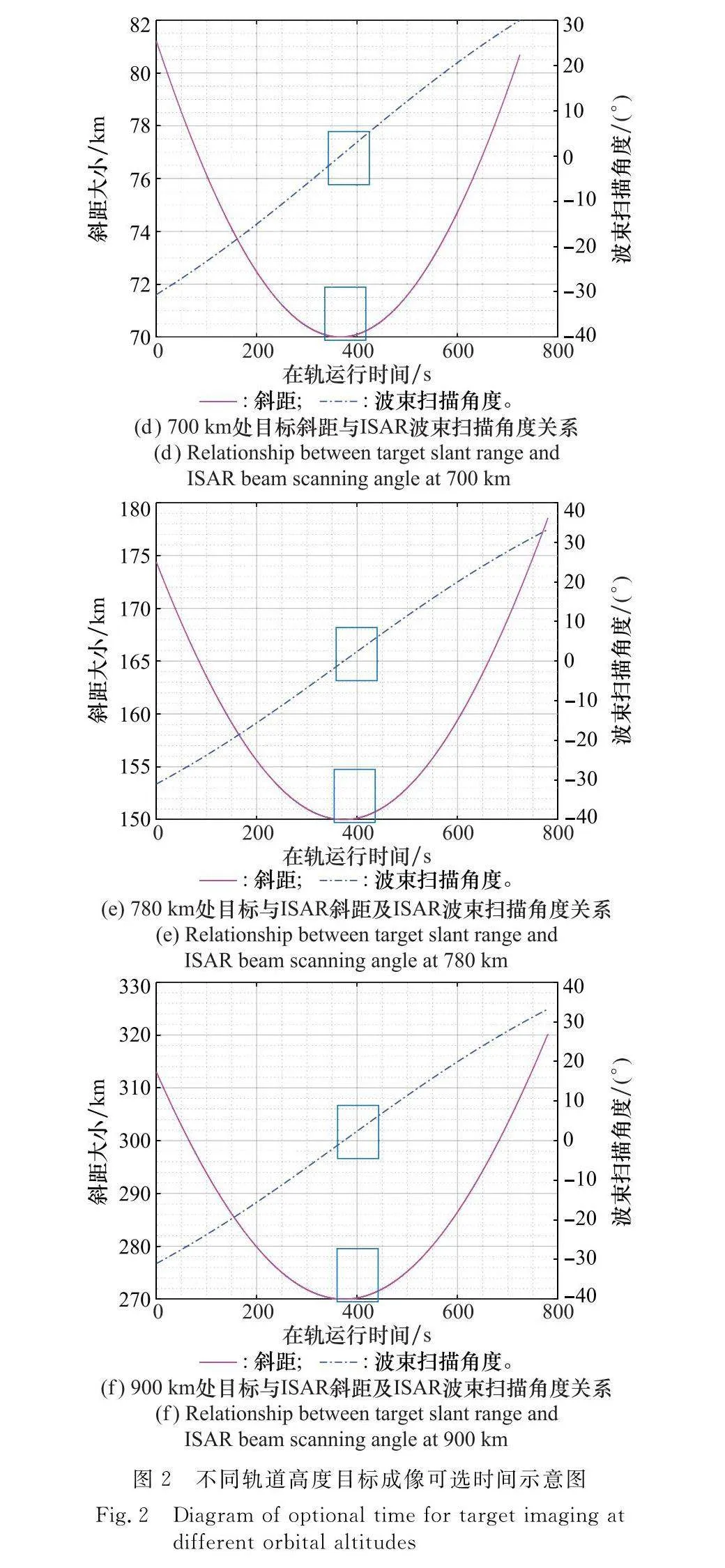
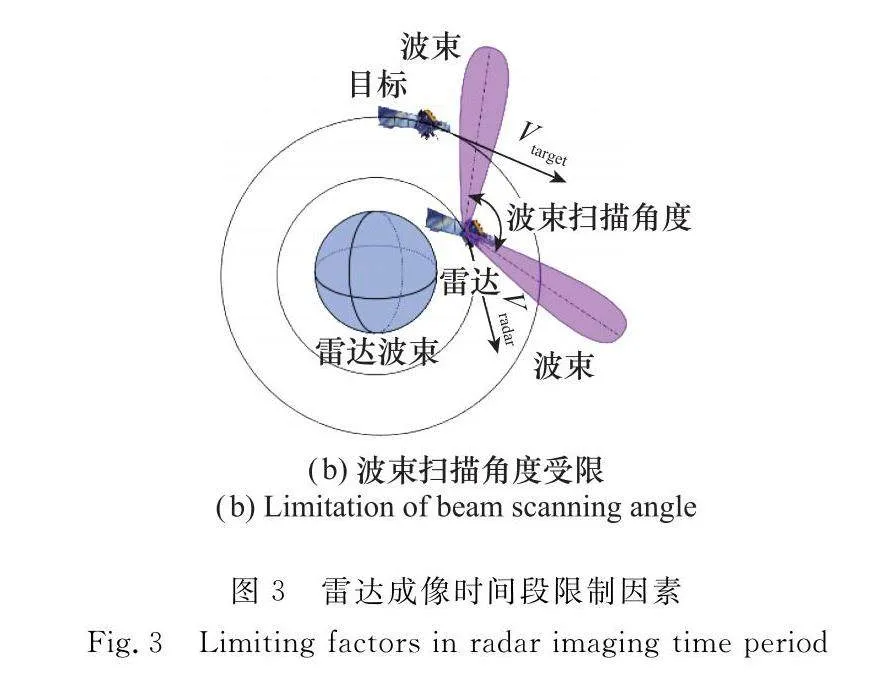
軌道可視弧段下，假定天基ISAR軌道高度為630 km，對軌道高度分別為700 km、780 km及900 km的目標進行跟蹤成像。依據表1，Ka波段天基ISAR波束掃描范圍為±15°，軌道可視弧段下，滿足雷達波束掃描范圍條件下的天基ISAR LOS與空間目標速度夾角的變化量如圖2（a）～圖2（c）所示，該時刻對應的波束掃描角度及斜距由圖2（d）～圖2（f）給出。Ka波段下，為滿足對空間目標高分辨率成像要求，方位分辨率要求達到0.05 m，對應有效旋轉角度為6°。依據圖2（a）～圖2（c），在雷達波束掃描范圍下，最大LOS夾角變化量可達60°，滿足方位分辨率要求的可選成像時刻較多。但由圖2（d）～圖2（f）可知，ISAR掃描角度在0°附近時，空間目標與天基ISAR作用距離最近，選取此時段作為成像時刻可使回波SNR最大，此時ISAR位于空間目標正下方附近，由于二者軌道相對傾角差較小，可近似認為天基ISAR與空間目標共面。軌道不可見弧度與ISAR波束掃描受限示意圖如圖3所示。

2.2 NESZ推導

以雷達系統NESZ來考量不同軌道高度目標在ISAR波束不同照射角度下，距離對可成像時間段的影響。NESZ是衡量雷達對弱目標成像能力的指標，其物理意義為當雷達圖像輸出SNR為0 dB時，對應的目標后向散射系數，表達式如下：

式中：R為雷達與目標距離，與二者軌道高度差相關;ν為雷達與目標的相對速度，與二者軌道高度差相關;Ka波段系統NESZlt;-18 dB；天線波束垂直指向正上方。

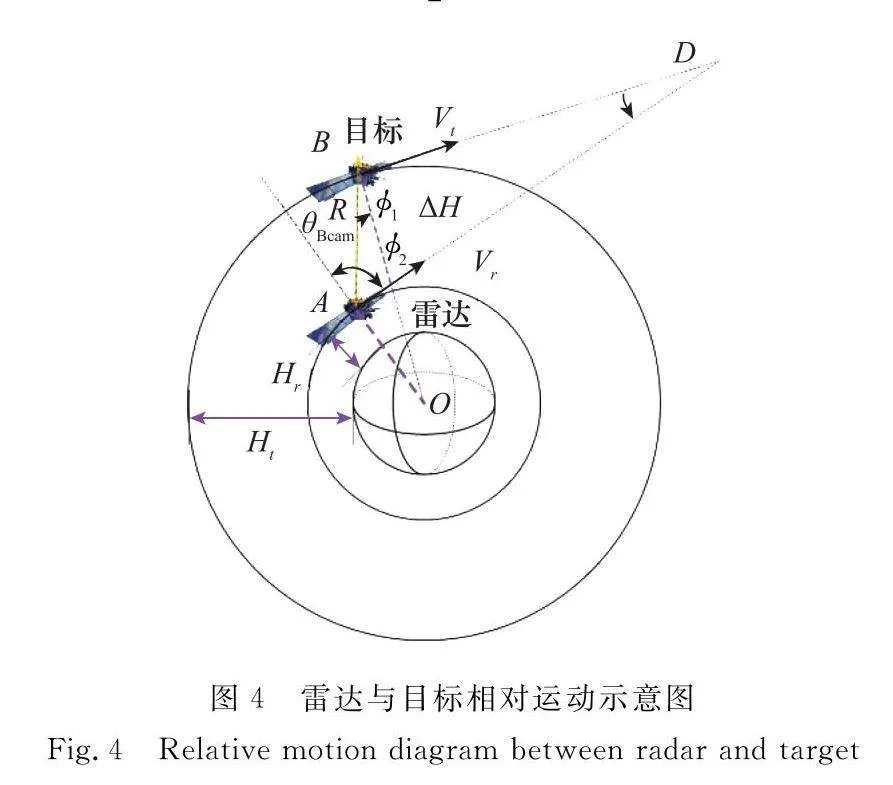
求解ISAR與目標速度夾角問題示意圖如圖4所示，θ_Beam，H_r，ΔH分別為波束掃描角度，ISAR軌道高度與目標軌道高度差；θ為雷達與目標速度相對夾角；?₂為LOS與ISAR速度夾角。

斜距R在ΔOAB中可用余弦定理表示為

式中：R_r及R_t可表示為

R_Earth為地球半徑，?₁在ΔOAB中同樣可用余弦定理求解：

在ΔABD中利用內角和性質可求得θ：

因此，ISAR與目標相對速度ν計算如下：

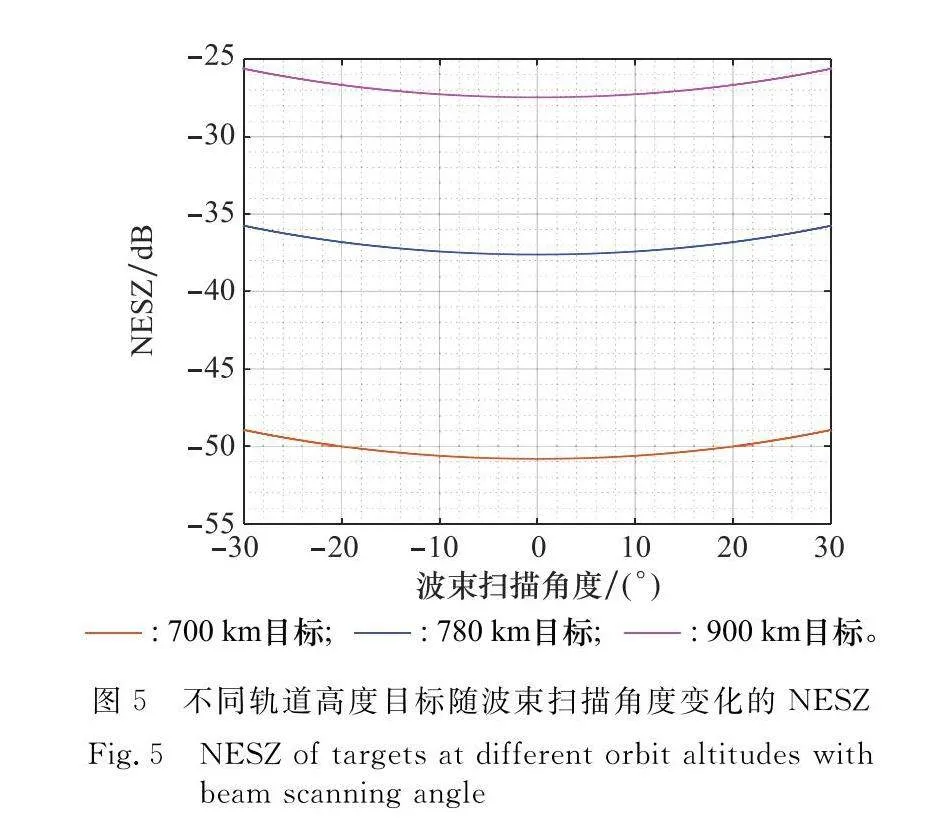
不同軌道高度差ΔH及波束掃描角下的NESZ：

圖5顯示了目標分別處于700 km、780 km及900 km軌道高度下NESZ隨ISAR波束掃描角度的變化關系。Ka波段天基ISAR波束掃描范圍為±15°，軌道高度為630 km情況下，對軌道高度為700 km、780 km及900 km目標在雷達波束掃面范圍內回波SNR均小于-18 dB。考慮到未來的技術發展，雷達波束掃描范圍會逐漸增大。天基ISAR在630 km軌道高度下，對空間目標成像時，隨著作用距離的增大，在大波束掃描范圍下，NESZ也會出現小于-20 dB的情況。

3 回波模型及平動補償

3.1 回波模型

圖6為ISAR對軌道目標成像幾何結構，目標位于笛卡爾坐標系（X，Y，Z）中，稱為目標本體坐標系，原點O為目標旋轉中心和參考成像中心。為忽略地球自轉對坐標系的影響，選取地心慣性坐標系（earth center inertial coordinates system， ECI）（X_S，Y_S，Z_S）為雷達參考坐標系，以地心O_s為原點，R_a表示ISAR與目標旋轉中心的距離，在成像初始時刻，雷達以俯仰角φ₀觀察目標。

ISAR成像中，發射信號常采用線性調頻信號^［19］，在軌目標任意一點P（x_p，y_p，z_p）在t_m時刻回波可表示為

式中：T_p，f_c，γ分別代表脈沖寬度、載頻及調頻率；rect（u）為矩形窗函數；t=t_m+t_r為全時間；t_r為快時間；t_m為慢時間；σ_p代表反射系數。經過脈沖壓縮以及距離向傅里葉變換后，回波可以寫為

ISAR成像過程中瞬時斜距R_p（t_m）可表示為

式中：R_a（t_m）為平動分量;R_rot（t_m）為轉動分量，可表示為

式中：rot（t_m）表示旋轉矩陣；P=［x_p，y_p，z_p］^T為P在目標本體坐標系的位置向量;I_LOS為沿LOS的單位向量，可表示為

式中：φ（t_m）為LOS在目標本體坐標系的俯仰角。

圖2（d）～圖2（f）中，不同軌道高度目標達到成像累積角度的時間較長，因此φ（t_m）隨t_m變化，導致I_LOS在CPI內時變，不能將I_LOS視為常量。為更好地描述在軌目標相對天基ISAR的非均勻轉動，選取二次多項式對φ（t_m）進行描述：

傳統ISAR成像目標大多數情況下會相對ISAR發生機動運動，包括橫滾、俯仰和偏航。然而，在軌目標受到軌道動力學的約束，大多數情況下不會發生劇烈機動。此外，通信衛星、遙感衛星等在軌工作時需要保持自身姿態穩定性。依據圖6，在軌目標沿軌道運動時，自身僅有俯仰軸發生變化，且其轉動速度為軌道角速度，因此旋轉矩陣rot（t_m）^［20］表示為

式中：y（t_m）為自成像開始時刻至t_m的俯仰角，可表示為

式中：ω_p為目標軌道角速度，sin θ與cos θ泰勒展開式如下：

結合式（20），將式（16）～式（19）代入式（15），保留至四階項，R_rot（t_m）可表達為

K₀，K₁等系數如下：

記：

因此，式（4）可重新表示為

其中，相位可以視為6個部分^［21］，式（24）等號右邊第1項對應方位多普勒;第2項對應距離壓縮;第3項為平動誤差，可通過常見運動補償手段補償；第4項為越距離單元走動項，可由楔形變換^［22］（keystone transform， KT）及廣義KT消除^［23］;第5項為方位相位誤差項;第6項為常數相位誤差，對成像無影響可以忽略。

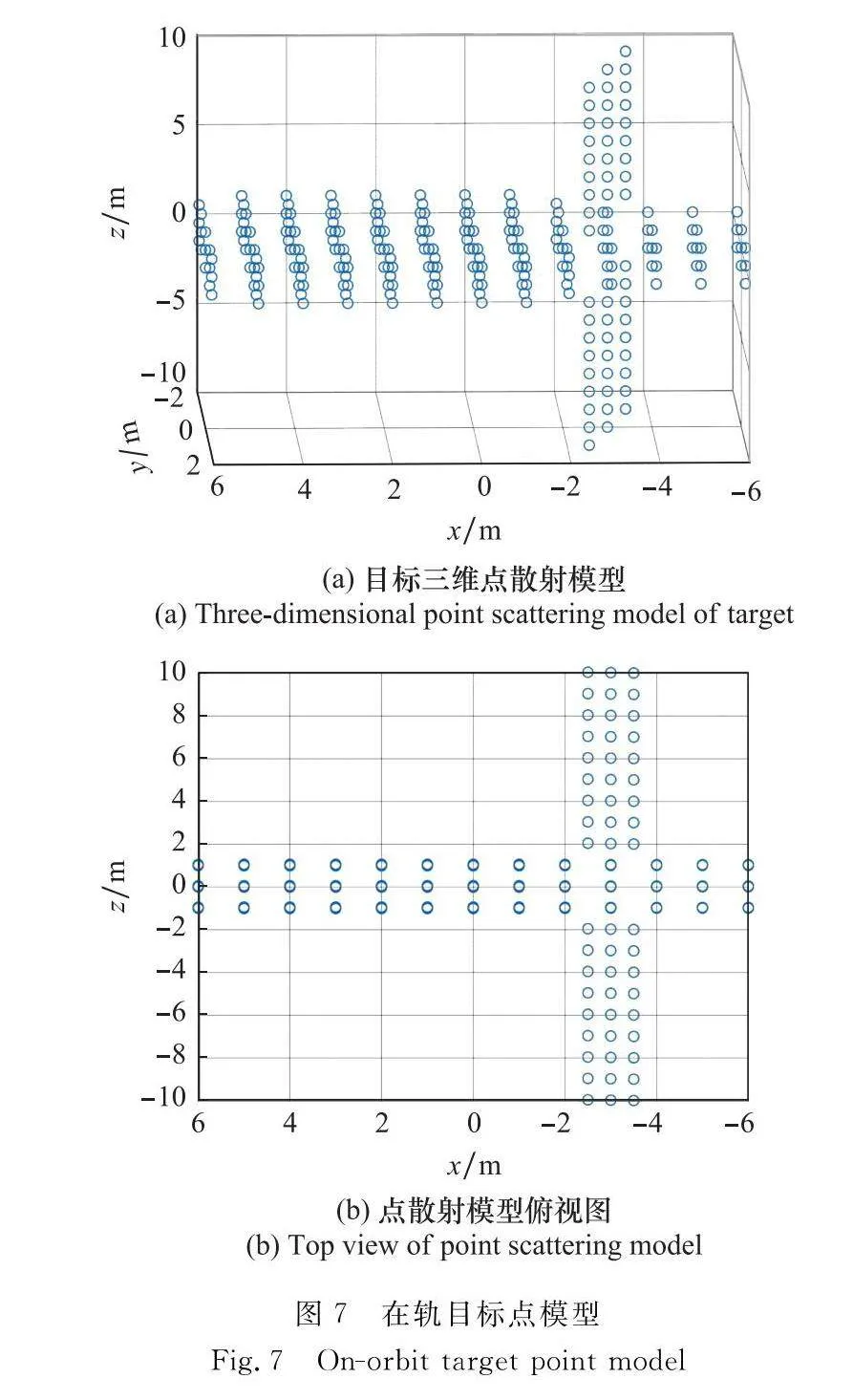
成像仿真中，方位向場景寬度D_a為200 m時可完整覆蓋成像場景，依據式（2），PRF下限為58 Hz，將PRF設置為100 Hz時可保證場景回波不混疊。在軌目標三維模型如圖7所示。

3.2 平動補償

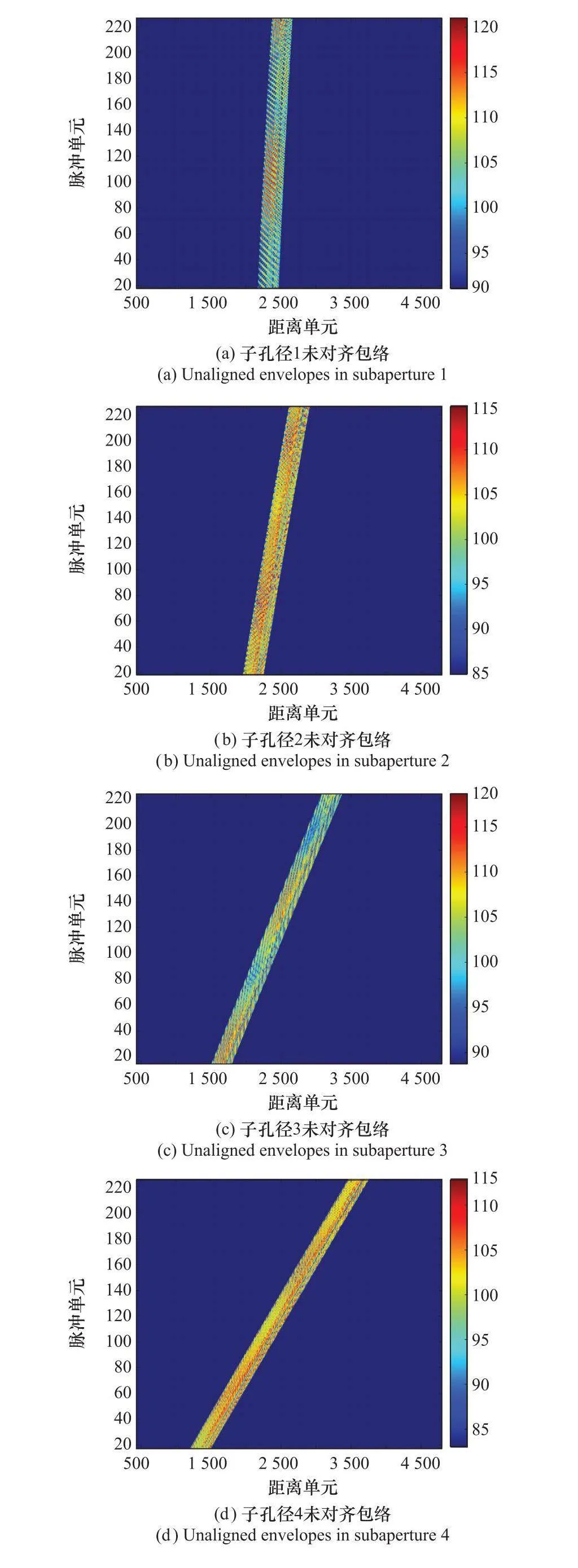
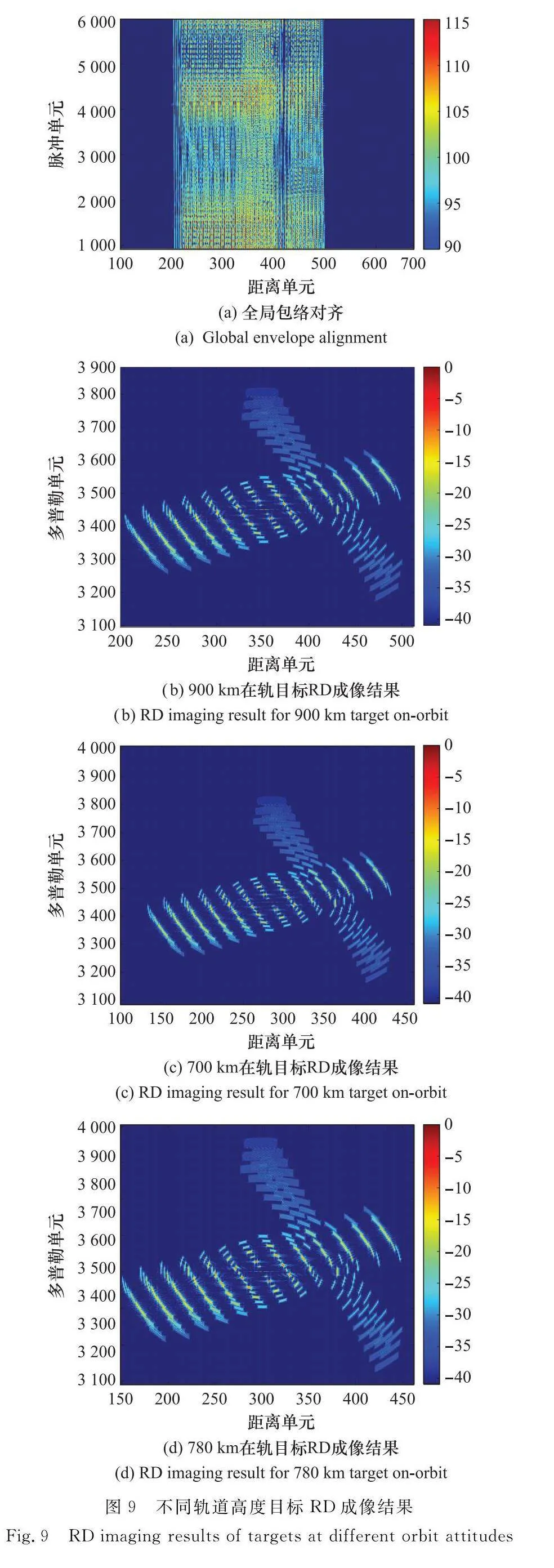
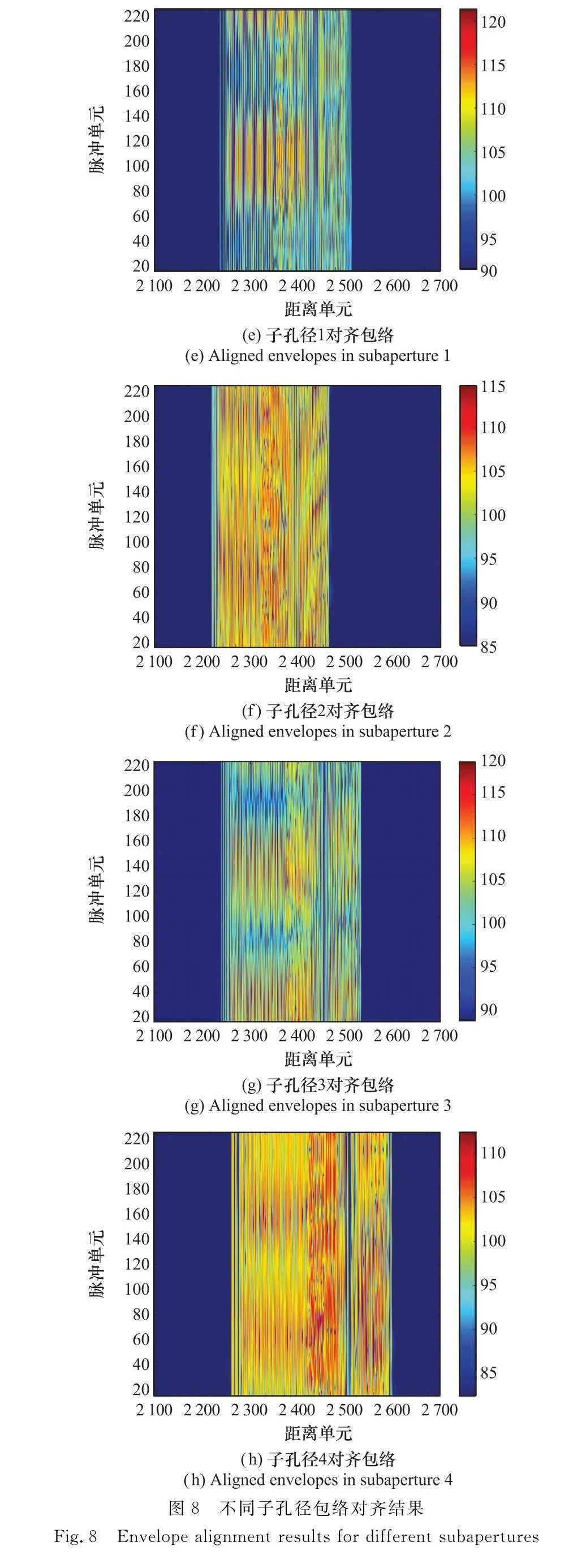
天基ISAR系統選取變采樣起始結合能量閾值門限的方法獲取在軌目標的回波。變采樣起始方法將回波方位向劃分為多個子孔徑，通過劃定每個子孔徑內的成像幅寬來減少回波距離向數據量。平動補償分為包絡對齊和相位校正兩部分，依據文獻［24］，在天基ISAR對在軌目標成像過程中，包絡對齊選取子孔徑對齊加全局對齊的方法，利用累計互相關法實現子孔徑間的包絡對齊后，提取不同子孔徑內的平均包絡，基于最小均方誤差準則實現全局包絡對齊。相位校正則選擇特顯點法，可以通過Radon變換或最小方差方法來提取特顯點。有關子孔徑及全局包絡對齊的方法的詳細信息可以參考文獻［24］。以900 km在軌目標為例，給出其包絡對齊結果，圖8（a）～圖8（d）分別顯示了不同子孔徑的未對齊包絡。可以看出，在軌目標相對于天基ISAR的運動越來越劇烈。圖8（e）～圖8（h）顯示了不同子孔徑的對齊包絡。圖9（a）給出了全局包絡對齊后的結果，依據圖9（b）～圖9（d）不同軌道高度的在軌目標RD成像結果，可以看到，700 km、780 km及900 km高度軌道目標的成像在方位向及距離向均嚴重散焦，故對二維散焦原因及現有處理手段進行研究。

4 二維散焦問題分析

4.1 距離向散焦問題分析

目標成像圖是目標三維點散射模型在二維成像平面XOY上的投影，該平面定義為與有效旋轉矢量垂直且內含i_LOS的平面。ISAR對軌道目標成像期間，回波經運動補償后，目標繞旋轉中心點O做非平穩轉動，且方位向高分辨率使得成像累積角度較大，相干積累間隔內散射點在距離向的走動量大于距離分辨單元，發生越距離單元走動（migration though resolution cell， MTRC）現象。此外，由于ISAR距離分辨率較高，MTRC更易發生，且在長合成孔徑時間影響下，目標在ISAR波束照射范圍內的非均勻有效轉動令MTRC中的高階項不可忽略。

常規MTRC補償方法為KT，通過將（f，t_m）空間的數據重映射到（f，t′）空間進行尺度變換去除MTRC，映射關系為

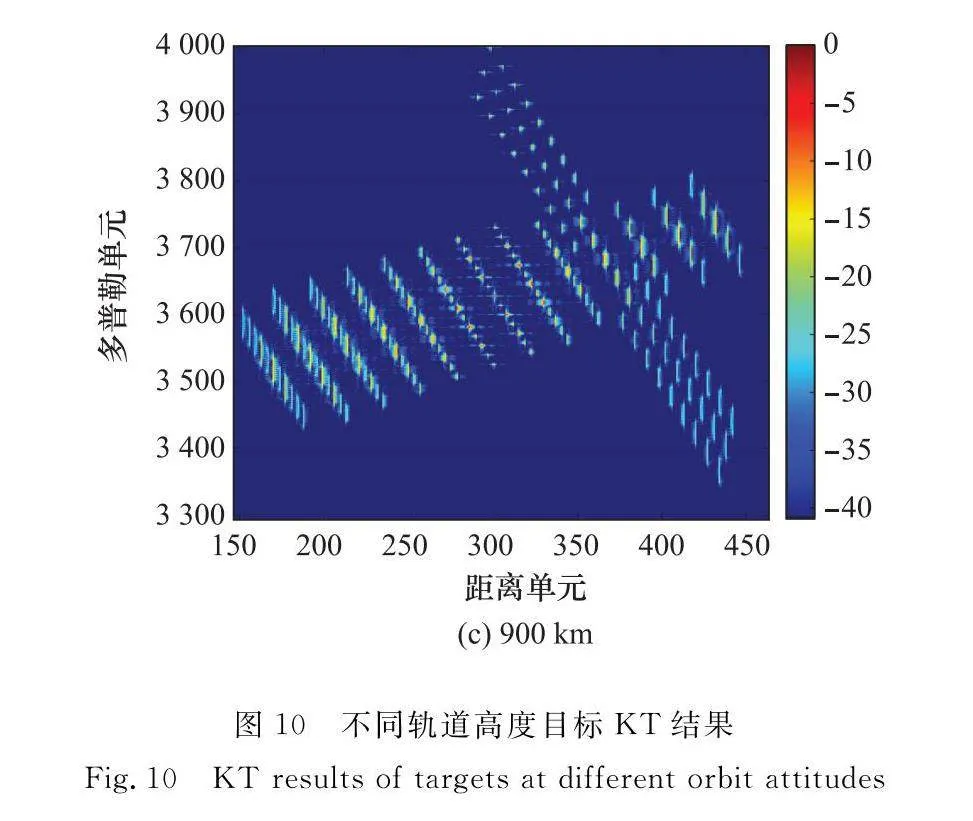
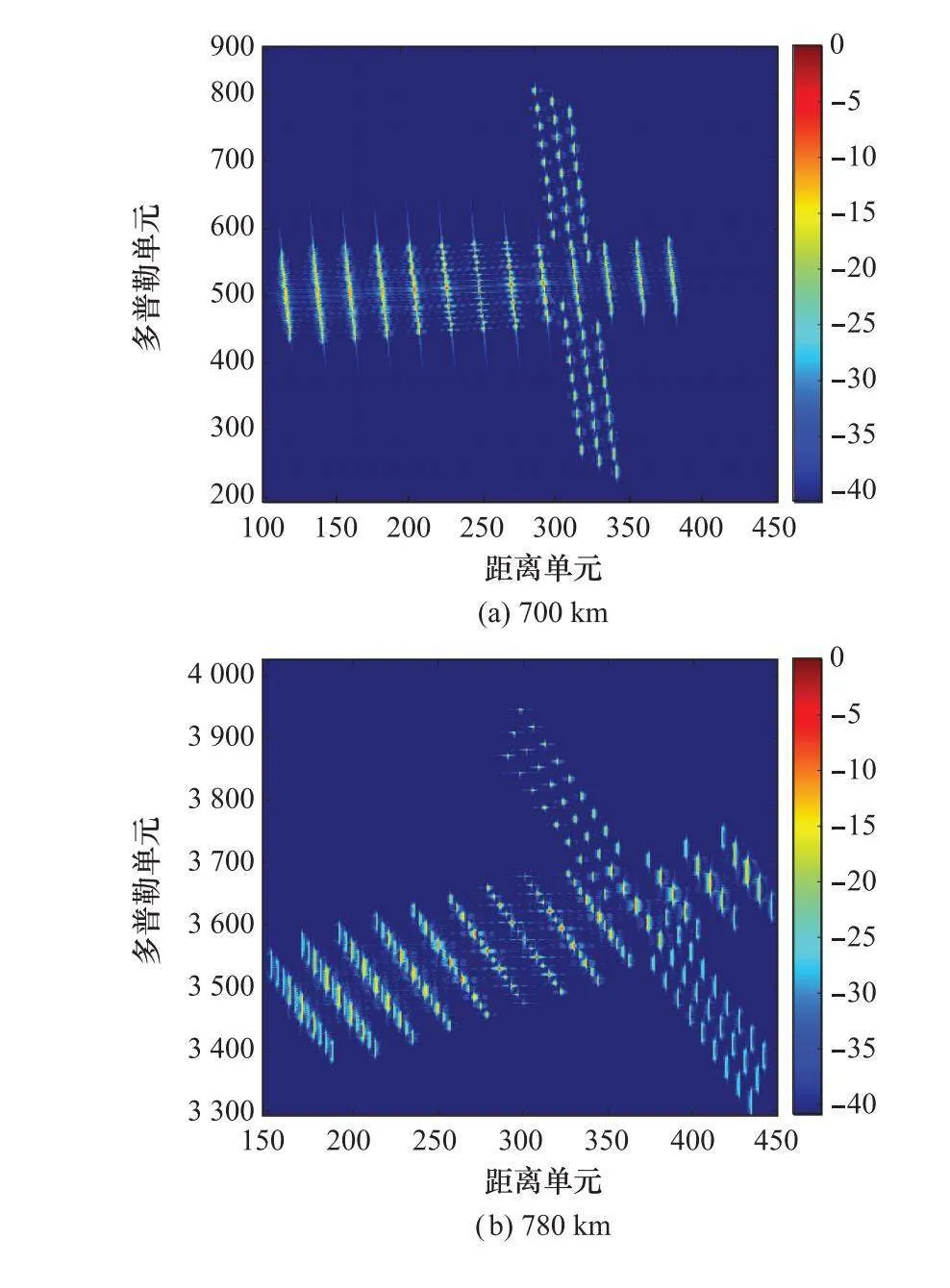
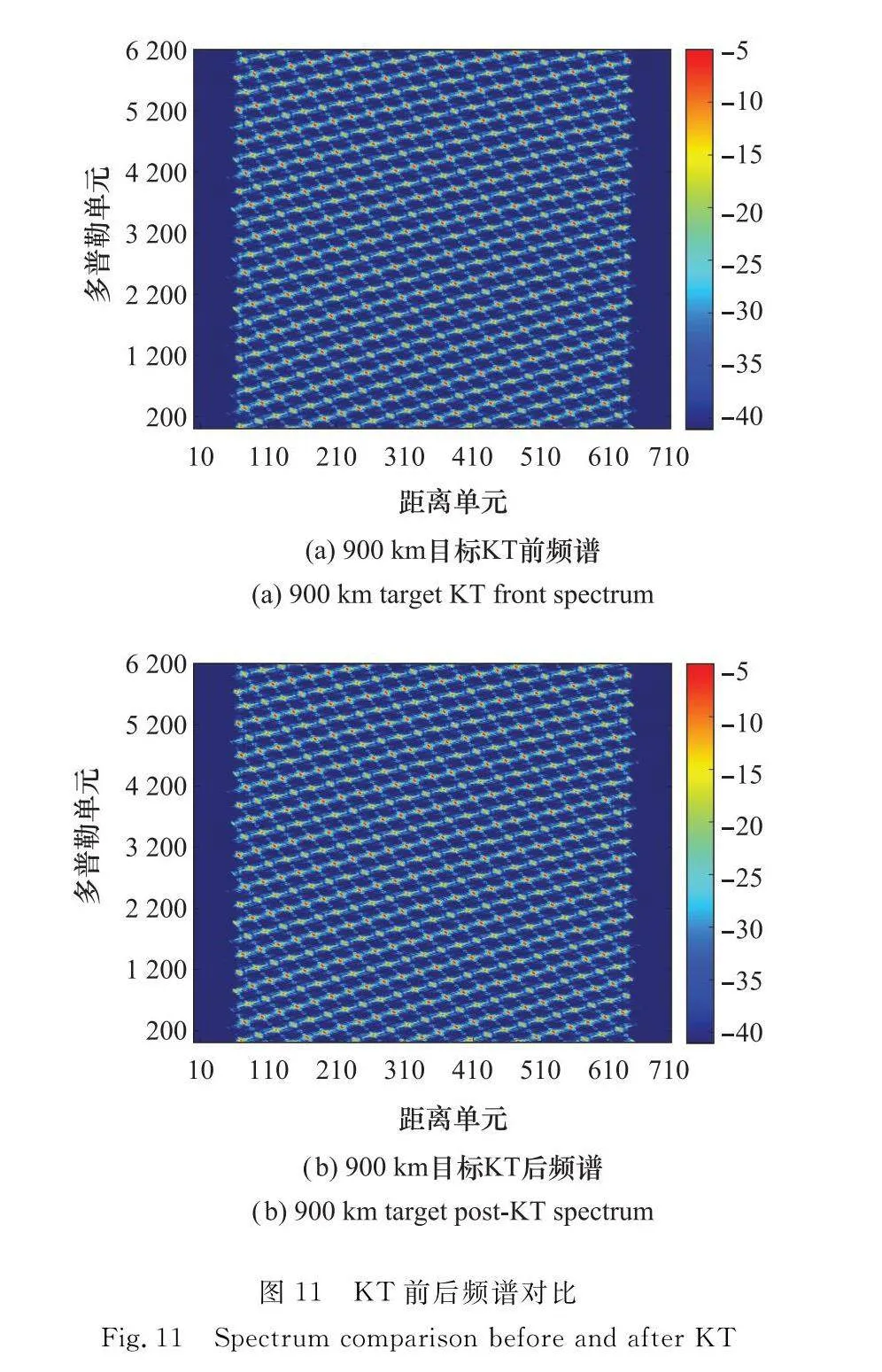
圖10為KT后不同軌道高度目標的成像結果，距離向散焦問題得到部分改善。圖11（a）和圖11（b）分別給出了KT前后的900 km目標頻譜。可以看到，KT變換后，在軌目標頻譜變換為梯形，結合圖10（c），經過傅里葉變換后，消除了距離向的一階MTRC，但仍舊存在散焦現象。

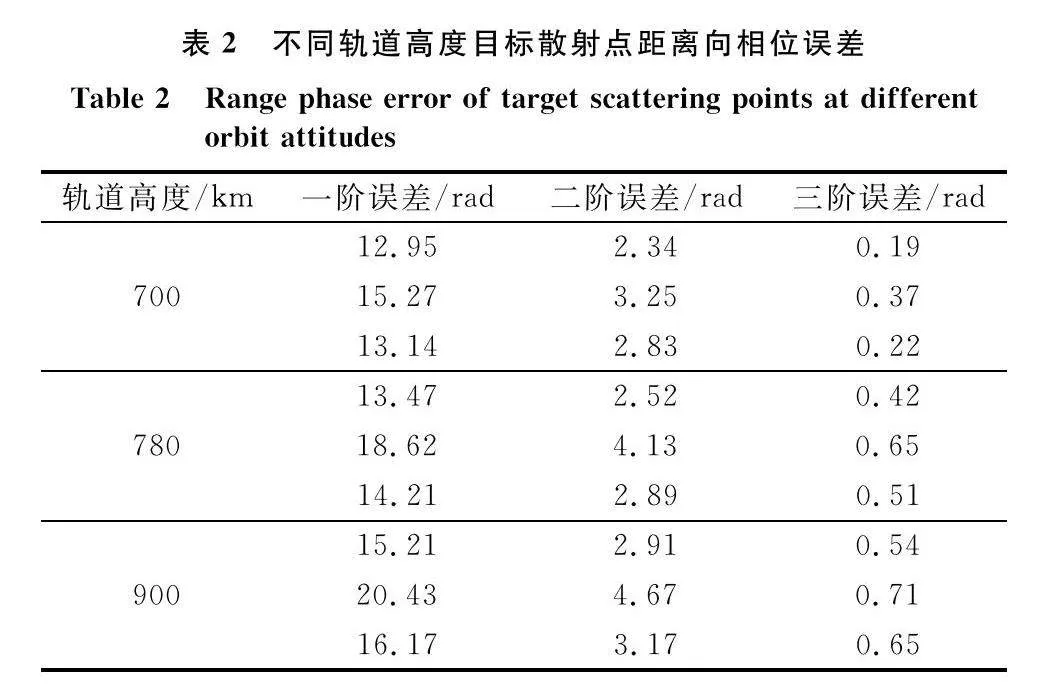
依據圖7空間目標點仿真模型對式（24）等號右邊第4項距離向相位誤差進行計算，結果在表2中給出。一般認為，相位誤差小于π/4即可忽略^［25］，在軌目標除旋轉中心外，距離向各散射點相位誤差須補償至t_m的二階項。由于KT對t_m進行線性變換，無法補償t_m的高階相位誤差，因此KT后圖像距離向仍舊散焦。

為獲取對軌道目標的精確成像結果，需要考慮其他MTRC校正方式。已有學者提出廣義KT （generalized KT， GKT）^［23］，其映射關系為

式中：n代表GKT階數。將天基ISAR回波中MTRC保留至三階，對式（24）進行平動補償并忽略掉常數相位差后：

取n=1/2，代入式（27）：

可以看到，GKT將空變相位誤差的二階項很好地消除了，但是仍舊存在殘余的一階及三階相位誤差，且距離向相位誤差與方位向相位誤差耦合在一起，增加了補償的難度。文獻［26-27］在使用了GKT后，采用了相關類函數逐個距離單元內對信號的剩余相位進行補償計算，使得補償相位誤差計算量顯著增加。為了能夠實現天基ISAR的在軌實時成像，仍舊需要研究計算復雜度較低的方法。

4.2 方位向散焦問題分析

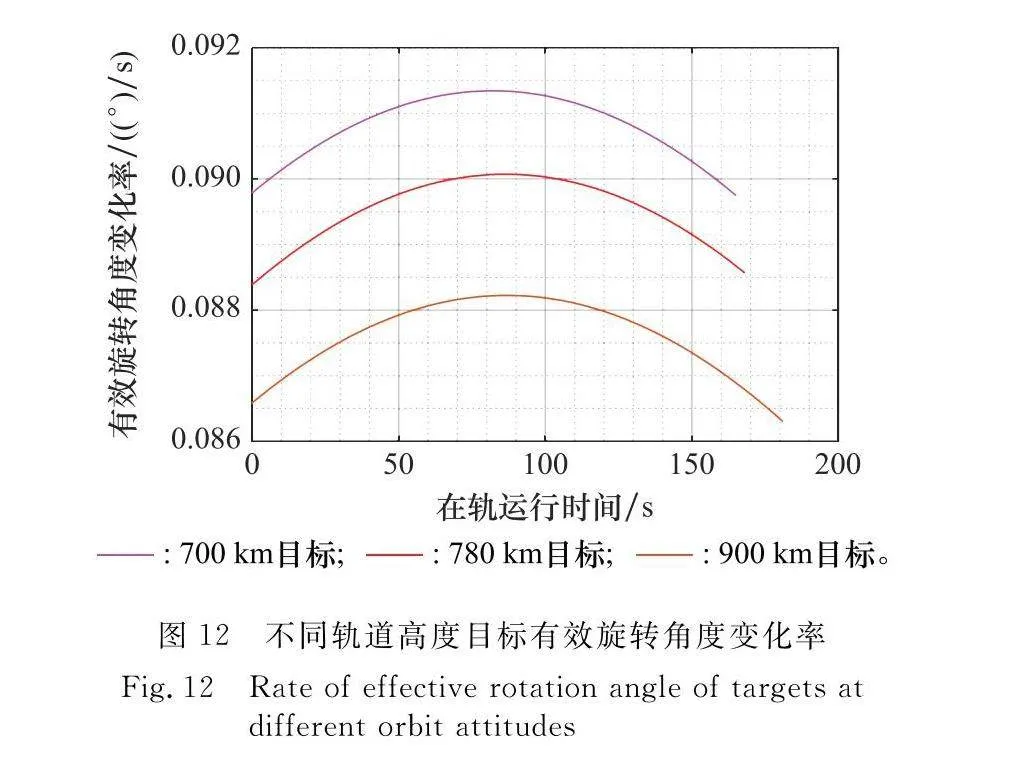
假設MTRC已經得到完全補償，但目標在ISAR LOS下做非均勻轉動，成像時間段內有效旋轉角度變化率時變，如圖12所示。P點多普勒頻率如下：

式中：w_e為有效轉動角速度；r_p為目標本體坐標系P點位置向量^［28］。

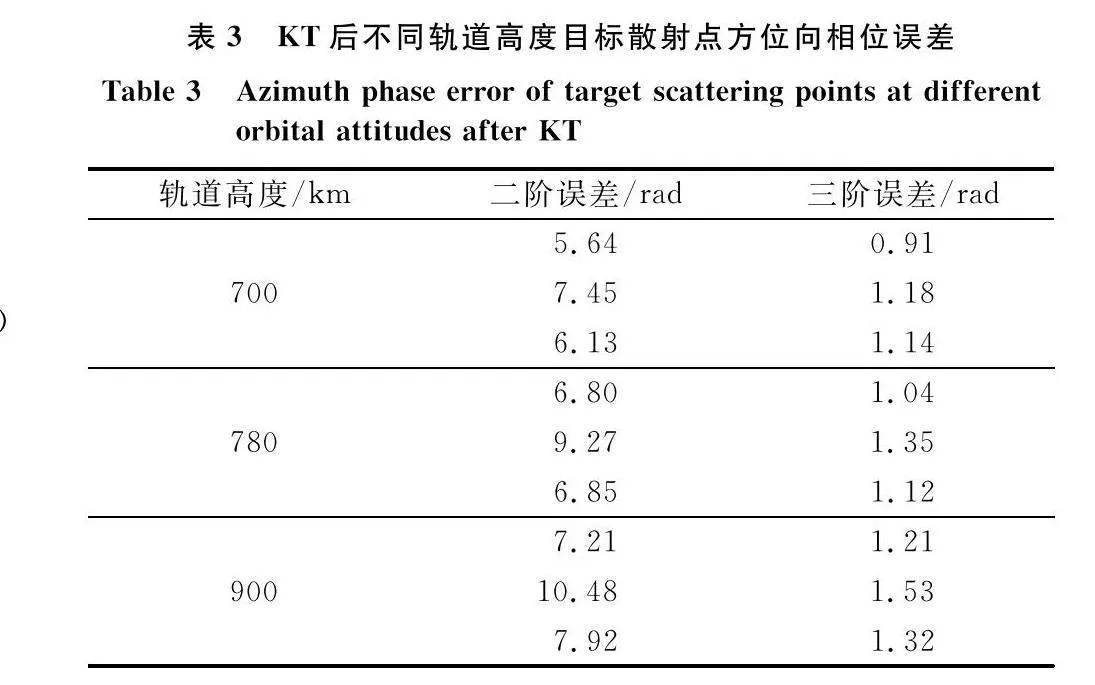
有效轉動角速度時變、散射點回波多普勒頻率時變，時變調頻率隨散射點位置變化， KT后圖像方位向仍舊散焦，依據圖7空間目標點仿真模型對式（24）等號右邊第4項方位向相位誤差計算結果在表3中給出。仍以π/4為標準來確定方位向相位誤差補償階數，KT后圖像方位向相位誤差存在高階項，需要補償至t_m的三階項。

天基ISAR對空間軌道目標成像時，方位向散焦主要由于高分辨率成像條件下，空間目標相對天基ISAR非均勻轉動所產生的高階相位誤差引起。為獲取聚焦良好的二維圖像，方位向應補償至空變相位誤差的三階項。

盡管超高分辨率ISAR成像及復雜運動機動目標ISAR成像已有大量研究開展^［29-32］，由此衍生出距離瞬時多普勒（range instantaneous Doppler， RID）算法^［33］、自聚焦算法^［19-21］等成像方法。RID算法通常分為兩類：參數化方法和非參數化方法。參數化方法如文獻［28-29］，將距離單元內的回波建模為線性調頻（linear frequency modulated， LFM）信號或三次相位信號，通過估計每個距離單元內的信號參數并補償相位誤差來實現復雜機動目標的ISAR成像。然而，參數方法將每個距離單元視為一個單獨的部分，忽略了目標旋轉運動的完整性，這降低了參數估計的精度，增加了計算復雜度。非參數化方法包括短時傅里葉變換（short-time Fourier transform， STFT）^［34］、連續小波變換（continuous wavelet transform， CWD）^［35］、Wigner-Ville分布（Wigner-Ville distribution， WVD）^［36］和分數傅里葉變換（fractional Fourier transform， FrFT）^［37］，均使用基于時頻分布（time-frequency distribution， TFD）的方法來實現ISAR成像。由于與天基ISAR相比，空間軌道目標的運動相對較慢，因此空變相位誤差參數較小，非參數方法在精確估計小的運動參數方面遇到了挑戰。文獻［19］中使用子陣平均最小熵，解決了ISAR對艦船成像過程中空變相位誤差的問題，但基于低階空變相位誤差系數對高階空變相位系數進行近似時，需要考慮先驗知識。此外，對空間軌道目標成像過程中，使用一階近似無法滿足高階空變相位誤差小于π/4條件，因此無法使用天基ISAR成像場景。文獻［21］中基于參數化最小熵方法，解決了傳統ISAR成像場景中機動目標的空變相位誤差問題。但是，文中成像CPI較短，ISAR成像過程中LOS不變這一情況不滿足天基ISAR成像情形，也沒有考慮高階空變相位誤差。綜上，仍舊需要研究天基ISAR成像過程中大轉角，長CPI的高分辨率成像算法。

4.3 在軌目標與天基ISAR運動特性分析

極坐標格式化算法^［38］可以有效解決大轉動角度下目標相對ISAR非均勻轉動的問題，但需對目標旋轉參數進行精確估計。因此，需要對在軌目標與天基ISAR的相對運動特性進行分析。

在巡視模式下，天基ISAR可以利用雷達跟蹤技術獲取目標的斜距及運動參數，從而輔助成像過程中的包絡對齊。還可以利用單脈沖技術測量在軌目標相對天基ISAR的俯仰角和方位角，結合天基ISAR測距信息及天基ISAR自身軌道參數，對在軌目標的軌道參數進行計算。

包絡對齊精度通常要求達到1/8個距離分辨單元。然而，由于天基ISAR成像的分辨率較高，5 cm分辨率下，基于目標運動參數估計所計算的在軌目標相對天基ISAR斜距精度需要達到毫米級，在雷達存在觀測噪聲的前提下，即便選取精度更高的Jerk模型^［39］和無跡卡爾曼對在軌目標進行跟蹤，也無法達到如此高的跟蹤精度。但可以基于卡爾曼濾波器得到的目標運動參數信息設置運動參數搜索區間，基于包絡最小熵或均方誤差準則，利用粒子群優化算法進行運動補償，因此在軌目標相對天基ISAR可視為半合作目標。

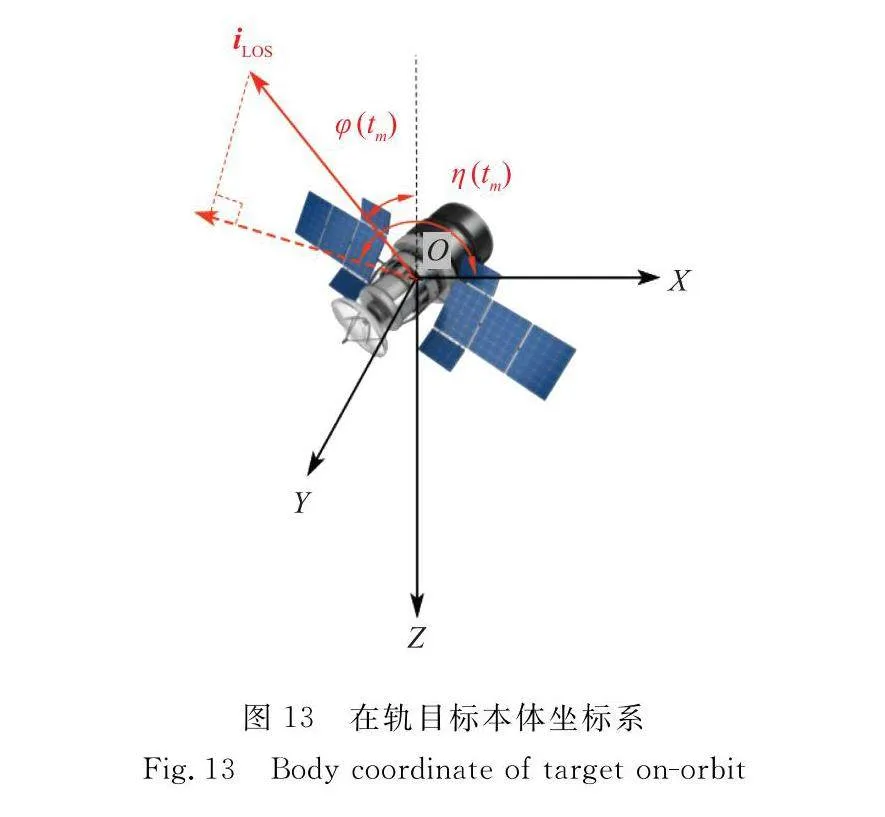
此外，天基ISAR在巡視模式下發現在軌目標后，需要轉為跟蹤模式，靠近目標對其近距離成像。這一過程中，在軌目標本體坐標系如圖13所示，φ（t_m）和η（t_m）為LOS在t_m時刻的俯仰角和方位角。天基ISAR可以通過單脈沖技術測量到目標的俯仰角和方位角，當天基ISAR位于在軌目標的正下方時，雷達波束指向正上方，利用回波時延τ計算的在軌目標斜距可近似為在軌目標與天基ISAR的軌道高度差。結合天基ISAR與目標的在軌幾何關系，利用正余弦定理，結合天基ISAR自身軌道參數，可以對在軌目標的軌道參數進行粗略估計。

在軌目標任意時刻下的運動參數均可以由軌道六根數唯一確定^［16］，因此可以基于估計出的在軌目標軌道六根數，輔助天基ISAR成像。為獲得高分辨率的天基ISAR圖像，需要對回波信號中的距離向和方位向的誤差相位進行補償。但基于以上策略，需要分析誤差補償精度是否小于π/4。天基ISAR對在軌目標進行軌道參數的估計時，由于觀測噪聲的影響，單脈沖測角、雷達跟蹤等手段存在一定的誤差，從而影響到對在軌目標的軌道參數估計。在Ka波段，5 cm分辨率的條件下，在軌目標的軌道參數能否滿足高階空變相位誤差的補償精度仍有待研究，因此也無法將在軌目標視為合作目標。綜上分析，應將在軌目標視為半合作目標，因此仍需要研究合適的參數估計方法，結合在軌目標相對天基ISAR的半合作關系為極坐標格式化方法進行參數的先驗估計。

5 結 論

本文基于天基ISAR對共面軌道目標高精度成像場景，研究了天基ISAR在軌運行的兩種工作模式及減少天基ISAR回波數據方案，并推導了基于天基ISAR波束掃描角度及天基ISAR與目標軌道高度差的NESZ表達式，依據天基ISAR與空間軌道目標相對運動關系，討論了天基ISAR對軌道高度分別為700 km、780 km、900 km的空間目標二維高分辨率可成像時間段。并對可成像時間段內目標ISAR圖像的二維散焦原因進行詳細分析，通過數值模擬確定了ISAR圖像二維散焦誤差相位的階數大小，為對空間目標成像的天基ISAR體制、成像時間段選取及信號處理設計提供了一定的理論依據。

參考文獻

［1］MARCHETTI E， STOVE A G， HOARE E G， et al. Space-based sub-THz ISAR for space situational awareness—concept and design［J］. IEEE Trans.on Aerospace and Electronic Systems， 2022， 58（3）： 1558-1573.

［2］周葉劍， 馬巖， 張磊， 等. 空間目標在軌狀態雷達成像估計技術綜述［J］. 雷達學報， 2021， 10（4）： 607-621.

ZHOU Y J， MA Y， ZHANG L， et al. Review of on-orbit state estimation of space targets with radar imagery［J］. Journal of Radars， 2021， 10（4）： 607-621.

［3］AVENTR K， SHELTON J D， BROWN P. The ALCOR C-band imaging radar［J］. IEEE Antennas and Propagation Magazine， 1996， 38（3）： 16-27.

［4］CAMP W W， MAYHAN J T， O’DONNELL R M. Wideband radar for ballistic missile defense and range-Doppler imaging of satellites［J］. Lincoln Laboratory Journal， 2000， 12（2）： 267-280.

［5］VIRGILI B B， LEMMENS S， KRAG H. Investigation on Envisat attitude motion［C］∥Proc.of the Deorbit Workshop， 2014.

［6］Fraunhofer FHR Lab. Space observation radar TIRA［EB/OL］. ［2023-10-20］. https：∥www.fhr.fraunhofer.de/en/theinstitute/technical-equipment/Space-observation-radar-TIRA.html.

［7］周葉劍， 張磊， 王虹現， 等. 空間軌道目標的逆合成孔徑雷達成像質量分析［J］. 雷達學報， 2017， 6（1）： 17-24.

ZHOU Y J， ZHANG L， WANG H X， et al. Performance analysis on ISAR imaging of space targets［J］. Journal of Radars， 2017， 6（1）： 17-24.

［8］DU Y H， JIANG Y C. Parametric translational motion compensation of spaceborne ISAR imagery for earth-orbit targets based on parabola detection and entropy minimization［J］. Remote Sensing Letters， 2021， 12（2）： 160-168.

［9］尹建鳳， 李志， 李懷鋒， 等. 天基連續毫米波空間碎片探測雷達方案設想［J］. 國際太空， 2015（1）： 70-75.

YIN J F， LI Z， LI H F， et al. Concept for space based continuous millimeter-wave radar for space debris detection［J］. Space International， 2015（1）： 70-75.

［10］YANG S H， LI S Q， JIA X， et al. An efficient translational motion compensation approach for ISAR imaging of rapidly spinning targets［J］. Remote Sensing， 2022， 14（9）： 2208.

［11］曹星慧. 對空間目標的星載干涉ISAR三維成像技術研究［D］. 哈爾濱： 哈爾濱工業大學， 2011.

CAO X H. Research on 3D imaging techniques of space target via spaceborne interferometric ISAR［D］Harbin： Harbin Institute of Technology， 2011.

［12］孫吉利， 禹衛東， 鄧云凱. 高分三號衛星SAR工作模式與載荷設計［J］. 航天器工程， 2017， 26（6）： 61-67.

SUN J L， YU W D， DENG Y K. Design of working modes and payload of SAR for GF-3 satellite［J］. Spacecraft Engineering， 2017， 26（6）： 61-67.

［13］劉杰， 張慶君. 高分三號衛星及應用概況［J］. 衛星應用， 2018（6）： 12-16.

LIU J， ZHANG Q J. Overview of GF-3 satellites and applications［J］. Satellite Application， 2018（6）： 12-16.

［14］張澤. 空間目標的SAR/ISAR成像方法研究［D］. 哈爾濱： 哈爾濱工業大學， 2019.

ZHANG Z. Research on SAR/ISAR imaging method for space target［D］. Harbin： Harbin Institute of Technology， 2019.

［15］SHI L， YANG L， ZHAO L L， et al. NESZ estimation and calibration for Gaofen-3 polarimetric products by the minimum noise envelope estimator［J］. IEEE Trans.on Geoscience and Remote Sensing， 2021， 59（9）： 7517-7534.

［16］OLIVER M， EBERHARD G. 衛星軌道： 模型、方法和應用［M］. 王家松， 祝開建， 胡小工， 譯. 北京： 國防工業出版社， 2012.

OLIVER M， EBERHARD G. Satellite orbits： models， methods and applications［M］. WANG J S， ZHU K J， HU X G， Trans.Beijing： National Defense Industry Press， 2012.

［17］禹衛東， 朱兆達， 張興敢. 彈載 SAR 信號處理及其硬件實現［J］. 南京航空航天大學學報， 1997， 29（2）： 162-168.

YU W D， ZHU Z D， ZHANG X G. Ballistic SAR signal processing and hardware implementation［J］. Journal of Nanjing University of Aeronautics and Astronautics， 1997， 29（2）： 162-168.

［18］ZUBACˇA J， STOLZ M， SEEBER R M， et al. Innovative interaction approach in IMM filtering for vehicle motion models with unequal states dimension［J］. IEEE Trans.on Vehicular Technology， 2022， 71（4）： 3579-3594.

［19］YANG Z J， LI D， TAN X H， et al. An efficient ISAR imaging approach for highly maneuvering targets based on subarray averaging and image entropy［J］. IEEE Trans.on Geoscience and Remote Sensing， 2021， 60： 5102113.

［20］DING J B， LI Y C， WANG J D， et al. Joint motion compensation and distortion correction for maneuvering target bistatic ISAR imaging based on parametric minimum entropy optimization［J］. IEEE Trans.on Geoscience and Remote Sensing， 2022， 60： 5118919.

［21］WANG J D， ZHANG L， DU L， et al. Noise-robust motion compensation for aerial maneuvering target ISAR imaging by parametric minimum entropy optimization［J］. IEEE Trans.on Geoscience and Remote Sensing， 2019， 57（7）： 4202-4217.

［22］PERRY R P， DIPIETRO R C， FANTE R L. SAR imaging of moving targets［J］. IEEE Trans.on Aerospace and Electronic Systems， 1999， 35（1）： 188-200.

［23］ZHANG L， HE X H. Approach for airborne radar ISAR imaging of ship target based on generalized keystone transform［C］∥Proc.of the IEEE 10th International Conference on Signal Processing Proceedings， 2010.

［24］YANG S H， LI S Q， FAN H T， et al. An effective translational motion compensation approach for high-resolution ISAR imaging with time-varying amplitude［J］. IEEE Geoscience and Remote Sensing Letters， 2023， 20： 4007805.

［25］LI Z， XING M D， XING W， et al， A modified equivalent range model and wavenumber-domain imaging approach for high-resolution-high-squint SAR with curved trajectory［J］. IEEE Trans.on Geoscience and Remote Sensing， 2017， 55（7）： 3721-3734.

［26］KONG L J， LI X L， CUI G L， et al. Coherent integration algorithm for a maneuvering target with high-order range migration［J］. IEEE Trans.on Signal Processing， 2015， 63（17）： 4474-4486.

［27］ZHENG J B， SU T， ZHANG L， et al. ISAR imaging of targets with complex motion based on the chirp rate-quadratic chirp rate distribution［J］. IEEE Trans.on Geoscience and Remote Sensing， 2014， 52（11）： 7276-7289.

［28］HUANG P H， XIA X G， ZHAN M， et al. ISAR imaging of a maneuvering target based on parameter estimation of multicomponent cubic phase signals［J］. IEEE Trans.on Geoscience and Remote Sensing， 2022， 60： 5103918.

［29］WANG Y， JIANG Y C. Inverse synthetic aperture radar imaging of maneuvering target based on the product generalized cubic phase function［J］. IEEE Geoscience and Remote Sensing Letters， 2011， 8（5）： 958-962.

［30］于晨. 大轉角ISAR高精度成像方法研究［D］. 成都： 電子科技大學， 2022.

YU C. Research on high precision ISAR imaging technology with wide-angle［D］. Chengdu： University of Electronic Science and Technology of China， 2022.

［31］符吉祥. 大轉角ISAR運動補償和成像方法研究［D］. 西安： 西安電子科技大學， 2021.

FU J X. Study on wide-angle ISAR motion compensation and imaging methods［D］. Xi’an： Xidian University， 2021.

［32］楊利超. 超高分辨ISAR成像技術研究［D］. 西安： 西安電子科技大學， 2021.

YANG L C. Study on ISAR ultrahigh-resolution imaging techniques［D］. Xi’an： Xidian University， 2021.

［33］WANG Y， LIN Y C. ISAR imaging of non-uniformly rotating target via range-instantaneous-Doppler-derivatives algorithm［J］. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing， 2014， 7（1）： 167-176.

［34］CHEN V C， MICELI W. Time-varying spectral analysis for radar imaging of manoeuvring targets［J］. IEE Proceedings-Radar， Sonar and Navigation， 1998， 145（5）： 262-268.

［35］KIM K T， CHOI I S， KIM H T. Efficient radar target classification using adaptive joint time-frequency processing［J］. IEEE Trans.on Antennas and Propagation， 2000， 48（12）： 1789-1801.

［36］WANG R， JIANG Y C. ISAR ship imaging based on reassigned smoothed pseudo Wigner-Ville distribution［C］∥Proc.of the International Conference on Multimedia Technology， 2010.

［37］LI Z， ZHANG X D， YANG Q， et al. Hybrid SAR-ISAR image formation via joint FrFT-WVD processing for BFSAR ship target high-resolution imaging［J］. IEEE Trans.on Geoscience and Remote Sensing， 2022， 60： 5215731.

［38］LIPPS R， KERR D. Polar reformatting for ISAR imaging［C］∥Proc.of the IEEE Radar Conference， 1998： 275-280.

［39］MEHROTRA K， MAHAPATRA P R. A jerk model for tracking highly maneuvering targets［J］. IEEE Trans.on Aerospace and Electronic Systems， 1997， 33（4）： 1094-1105.

作者簡介

劉一飛（1999—），男，博士研究生，主要研究方向為天基ISAR高分辨率成像算法、天基ISAR系統設計。

禹衛東（1969—），男，研究員，博士，主要研究方向為SAR系統設計和研制、高分辨率SAR新體制、SAR成像處理、數據壓縮。

楊升輝（1997—），男，博士研究生，主要研究方向為高分辨率ISAR成像算法。

李世強（1967—），男，研究員，博士，主要研究方向為星載成像雷達新體制、星載SAR系統設計與仿真。