組網雷達系統高精度協同跟蹤和功率分配方法


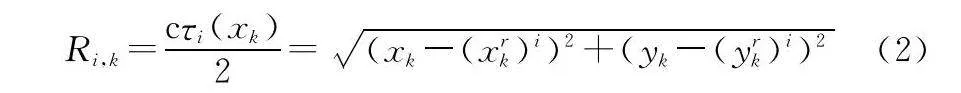
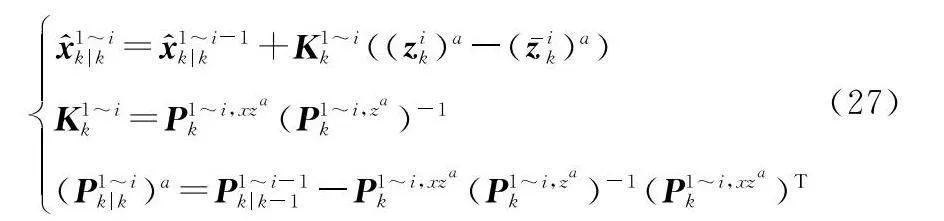
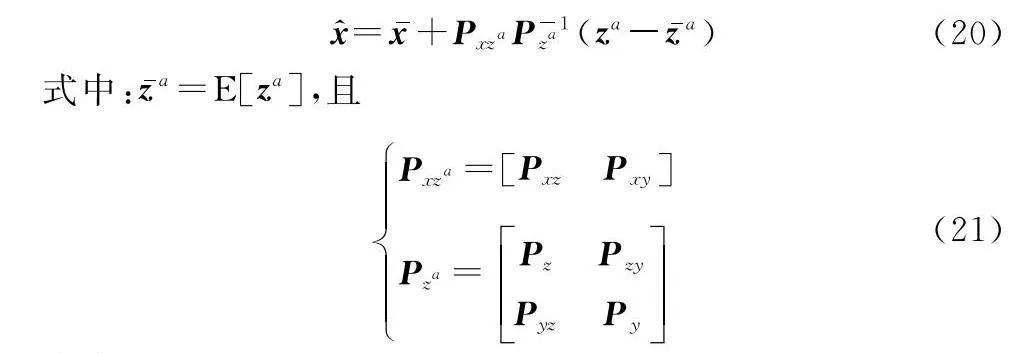
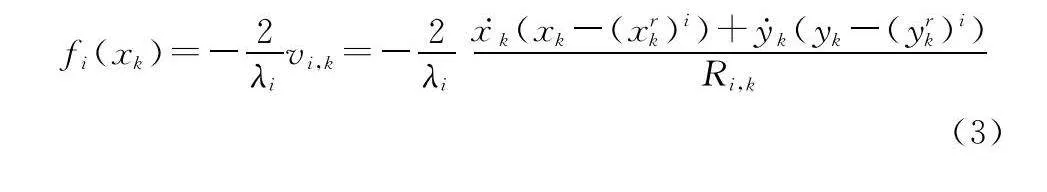



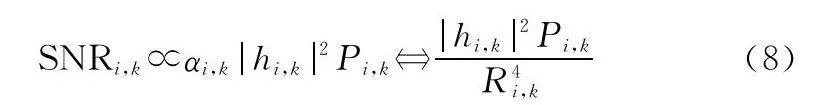
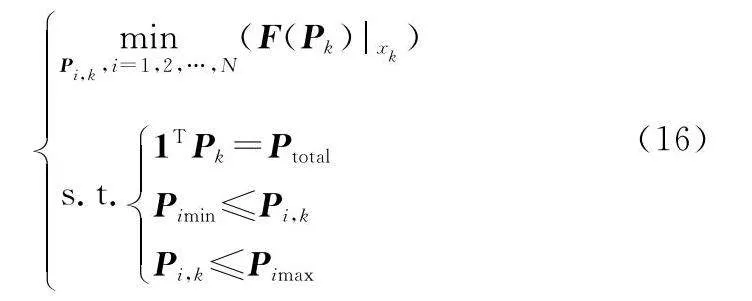

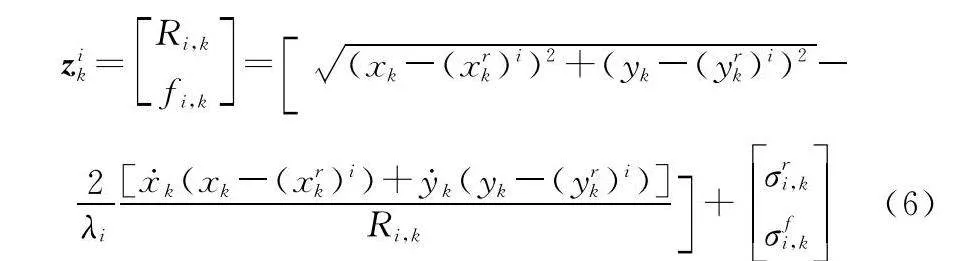
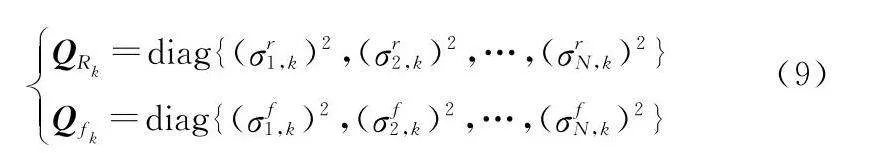


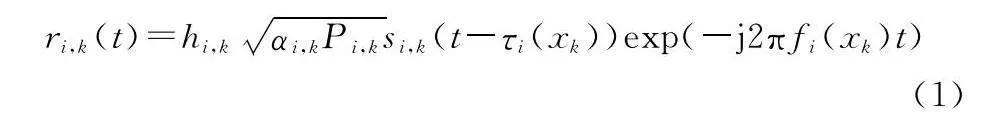
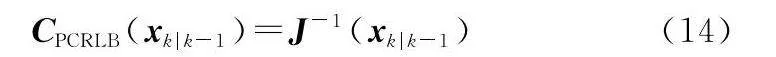
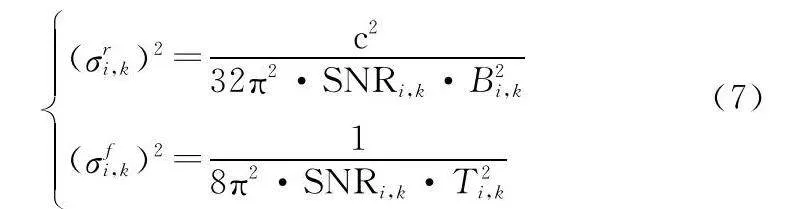


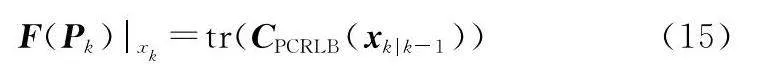

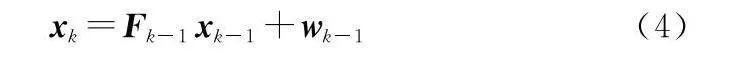

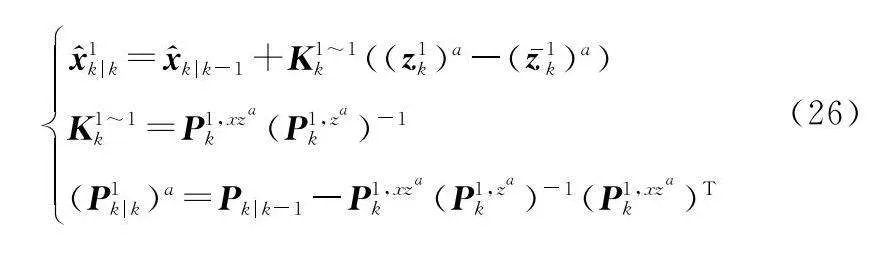
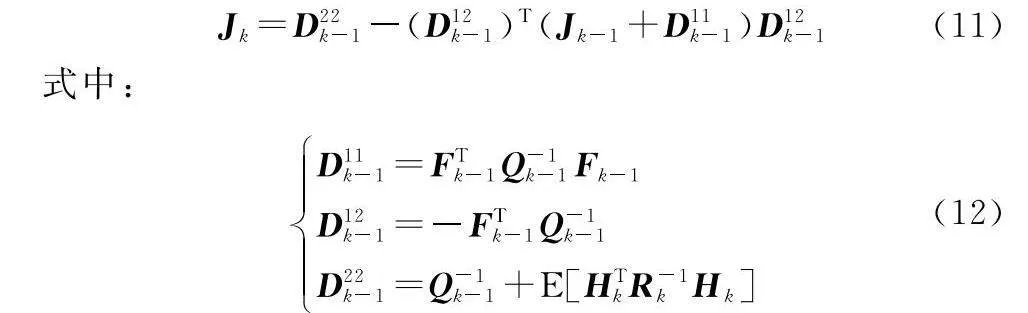
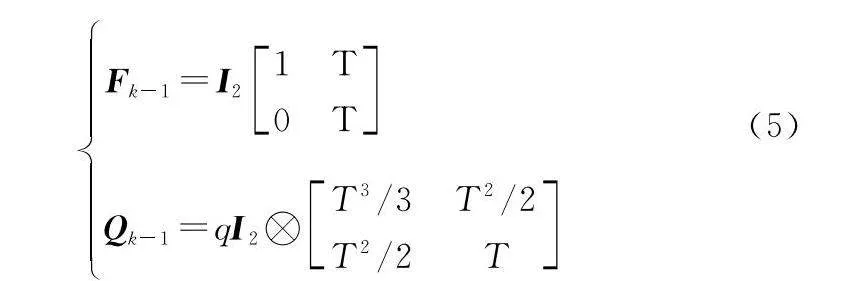
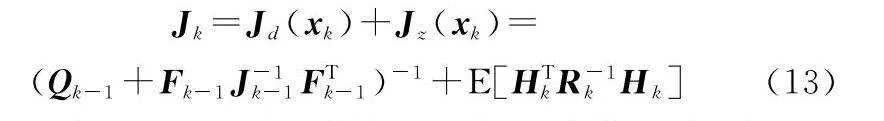
摘要: 分布式組網雷達系統可充分利用多雷達協同優勢提升動目標跟蹤性能。然而,在實際中,組網雷達系統的發射總功率受限且量測函數的高度非線性,都會導致目標跟蹤精度極大受限。針對上述問題,提出一種基于不相關轉換濾波(uncorrelated conversion based filter, UCF)的高精度目標協同跟蹤和資源管理方法,該濾波方法可充分提取有效量測信息,提升目標狀態估計性能,且該信息可作為整體框架的反饋信息進一步優化資源分配。首先推導了后驗克拉美羅下界作為優化準則,利用該準則給出當前時刻的最優資源分配;然后基于分配的功率資源,進行目標狀態估計;針對強非線性量測函數,提出一種UCF,利用不相關轉換提取更多原始量測中的信息,并將其用于線性最小均方誤差框架進行狀態估計,從而提高目標狀態估計性能。仿真結果驗證了所提方法的有效性。
關鍵詞: 組網雷達; 功率分配; 協同跟蹤; 不相關轉換; 非線性濾波
中圖分類號: TN 953
文獻標志碼: A
DOI:10.12305/j.issn.1001-506X.2024.11.14
High accuracy cooperative tracking and power allocation method in networked radar system
ZHANG Yingjie1, CHEN Hongmeng1,*, GAO Wenquan1, LAN Jian2, YE Chunmao1, CHEN Yan1
(1. Beijing Institute of Radio Measurement, Beijing 100854, China; 2. School of Automation Science and Engineering, Xi’an Jiaotong University, Xi’an 710049, China)
Abstract: Distributed networked radar system (NRS) can take full advantage of multi-radar synergistic features to improve the tracking performance of a moving target. However, in fact, the limited total transmitted power and the high nonlinearity of the measurement function of an NRS heavily restrict the target tracking performance. To solve these problems, a high accuracy cooperative tracking and resource allocation method is proposed, in which the uncorrelated conversion based filter (UCF) is utilized to improve the estimation performance by extracting effective measurement information. Moreover, this estimation can be considered as the feedback information for the framework to further optimize the performance of the resource allocation. Firstly, the posterior Cramer-Rao lower bound (PCRLB) is derived as the optimization criterion, which can be utilized to obtain the optimized resource allocation. And then according to the allocated power, the target state can be estimated. A UCF is proposed for strongly nonlinear measurement functions, which utilizes uncorrelated conversion to extract more information from the original measurements and applies it to a linear minimum mean square error framework for state estimation, thereby improving the performance of target state estimation. The simulation results verify the effectiveness of the proposed method.
Keywords: networked radar; power allocation; cooperative tracking; uncorrelated conversion; nonlinear filtering
0 引 言
隨著技術的發展和武器系統的更新迭代,現代戰爭中的傳統雷達系統面臨著愈發嚴峻的挑戰,先進的反輻射導彈技術、不斷進步的低空突防技術、高速發展的目標隱身技術以及日新月異的電子干擾技術構成了現代雷達的“四大威脅”[1-6]。在此背景下,傳統雷達系統不僅難以滿足作戰需求,甚至其生存能力也面臨嚴峻考驗[6]。在這種情況下,近年來組網雷達系統(networked radar system, NRS),例如多輸入多輸出(multiple-input multiple-output, MIMO)雷達等,受到了廣泛關注[3,5]。該系統由多個空間上分開的收發設備組成,采用多發射-多接收形式,各部分可獲取獨立的量測信息,并將接收到的信息傳輸給融合中心進行聯合處理,實現對目標的檢測、識別、定位、跟蹤等任務[5,7]。NRS利用多個雷達進行協同探測跟蹤等,具有遠優于傳統單雷達系統的性質,具體包括:① 采用收發分置,實現接收站無源工作,提高系統生存能力;② 多角度、大范圍區域覆蓋,獲取更多的目標信息,實現動目標高精度探測、跟蹤和識別;③ 多源信息融合有助于提升系統魯棒性,并增強系統探測跟蹤等能力。
雖然增加NRS中雷達數量,提高發射功率可有效提升對目標的探測、跟蹤、識別等性能。然而實際中,增大系統規模意味著融合處理中心劇增的數據處理壓力。同時,系統信息傳輸能力受限于通信傳輸帶寬,也制約了系統規模的增加,此外發射功率同樣會受到設備應用場景及硬件等因素的制約(如機載監視雷達、無人機載設備等),進一步限制了NRS中的雷達數量[6-9]。因此,亟需對雷達資源管理方法進行研究,通過合理分配雷達資源,充分發揮雷達協同性能,獲取盡可能高精度的測量信息,為復雜場景中的高精度動目標跟蹤提供有力支撐。
為了實現雷達資源有效利用,很多學者對雷達資源分配方法展開了研究,特別是針對功率分配和傳感器選擇等。現有比較流行的資源管理框架主要包括:① 資源一定情況下,最大化系統跟蹤精度;② 在給定跟蹤精度情況下,通過選擇最優的傳感器,實現最小化資源消耗。目前,常用的傳感器資源管理優化準則為后驗克拉美羅下界(posterior Cramer-Rao lower bound, PCRLB)準則[10],該準則是一種用于衡量無偏估計的一般方法。在目標跟蹤問題中,PCRLB定義為Fisher信息矩陣(Fisher information matrix, FIM)的逆,可給出最好均方誤差矩陣的一個下界[10],從而實現最優資源分配[6-7,9,11]。由于在實際中目標位置是估計量,因此需要NRS根據估計得到的目標狀態預測下一時刻目標狀態,從而對雷達資源進行提前分配。
現有研究文獻很大部分針對框架①下的NRS進行研究,通過優化功率、帶寬、信號有效時寬、采樣間隔及駐留時間等系統參數,實現目標跟蹤性能提升[4,11-15]。
文獻[14]針對多雷達系統目標定位問題進行研究,推導得到基于克拉美羅下界(Cramer-Rao lower bound, CRLB)準則的解析形式的功率分配算法,給出上述兩類優化框架下的功率分配問題優化解。文獻[4]針對分布式NRS中的多目標跟蹤問題進行研究,在功率分配的基礎上,聯合考慮節點選擇問題,并利用粒子濾波算法計算每個目標的狀態后驗分布,最優融合結果用于系統分配優化。文獻[15]中集中式MIMO雷達進行多目標跟蹤,構建了聯合功率分配及波形選擇優化函數,并利用容積卡爾曼濾波器(cubatare Kalman filter, CKF)獲取高精度狀態估計結果用于系統優化框架。文獻[5]針對組網雷達多目標跟蹤問題,重點考慮了功率分配和傳感器運動帶來的定位誤差等因素,推導了聯合功率分配和量測選擇算法,實現多目標精確跟蹤。
分析可知,目標跟蹤性能的提升依賴于系統優化機制,通過參數優化,改善系統對空間目標跟蹤能力,利用非線性濾波方法提升目標跟蹤精度,反饋高精度跟蹤結果從而提升系統優化效能。即系統的有效優化和目標的精確跟蹤相互耦合,特別是在復雜戰場環境中,整體系統的跟蹤性能會極大受限于跟蹤算法的性能優劣。上述研究文獻重點關注功率、帶寬等分配算法的優化及傳感器個數或位置等的選取,對于目標跟蹤中的反饋信息,即目標狀態及協方差等信息的精確化求解研究較少。
復雜戰場環境中目標跟蹤難題在于,實際雷達系統中的測量函數幾乎都是強非線性的,大噪聲強非線性等難題導致非線性估計面臨嚴峻挑戰,較差的估計精度會進一步影響系統優化性能,降低功率或帶寬等分配準確性,限制NRS整體探測跟蹤性能,一部分文獻對上述問題進行了初步探索研究。
在靜止目標定位精度和功率分配優化問題基礎上,文獻[6,9]重點研究了目標勻速直線運動場景下的功率分配方法,以貝葉斯CRLB(Bayesian CRLB, BCRLB)為優化函數,分別分析不同起伏雷達散射截面(radar cross section, RCS)模型、不同傳感器組合下的最優功率分配,并在此基礎上提升目標跟蹤精度。文獻[11,13]重點研究了復雜機動場景下,利用交互多模型濾波框架結合傳統非線性濾波方法進行目標狀態精確估計,有助于進一步優化功率分配結果。文獻[4,15]為了進一步提升系統優化性能,分別采用了粒子濾波方法和CKF方法進行目標狀態估計。
然而,上述文獻中所采用的方法,如擴展卡爾曼濾波器(extended Kalman filter, EKF)、無跡濾波器(unscented filter, UF)、CKF及求積卡爾曼濾波器(quadrature Kalman filter, QKF)等,基本上都可看作是基于線性最小均方誤差(linear minimum mean square error, LMMSE)的估計器[16-22]。而該類濾波器性能極大受限于其本身的線性結構,當量測具有較強的非線性時,量測與被估計狀態為明確的非線性關系,這與LMMSE估計器和量測的線性關系在本質上并不匹配,極大限制了LMMSE框架及相關濾波方法的估計性能,難以獲得高精度目標狀態估計[17,19,21]。
為應對上述難題,文獻[17,19]提出了一種基于量測不相關轉換的思想,通過對原始量測進行不相關轉換從而有效提取量測信息,突破了LMMSE框架限制,實現了真正意義上的非線性結構濾波,大幅提高了估計性能。因此,基于量測轉換的非線性濾波方法成為了應對強非線性問題的重點研究方向之一。
為了實現NRS中的功率合理分配,同時實現動目標高精度協同跟蹤,本文提出了一種高效功率分配下的基于不相關轉換的高精度目標跟蹤方法,主要思想如下:首先給出了目標跟蹤問題中的PCRLB框架,利用目標狀態預測的下一時刻PCRLB信息作為代價函數進行功率分配;而后利用分配的功率得到對應雷達的量測信息(噪聲統計量等),通過基于不相關轉換濾波(uncorrelated conversion based filter, UCF)方法,從原始量測中獲取更多的有效信息,實現高精度協同跟蹤,并將精確估計信息反饋到功率分配框架中,實現最優功率分配。仿真結果驗證了本方法的有效性。
本文主要工作包括如下兩方面:
(1) 針對強非線性跟蹤問題(大量測噪聲、機動目標跟蹤等),提出一種基于UCF的高效功率分配方法,通過更多量測信息提取,實現目標狀態的精確估計,可有效優化功率分配性能,進而提升機動目標跟蹤性能。
(2) 針對多傳感量測信息實時處理問題,提出基于不相關轉換組網雷達序貫濾波算法,克服濾波算法高維采點導致的計算復雜度過高難題,實現組網雷達多量測實時精確目標跟蹤。
1 問題描述
1.1 信號模型
本文考慮如下場景:在空間中,有一個目標做近似勻速直線運動(nearly constant velocity, NCV),N中包含N部二維雷達(量測信息為徑向距離和多普勒頻移),每部雷達僅接收自身回波數據,并將量測信息在融合中心進行融合處理。在總功率一定的情況下,優化每部雷達的發射功率,利用本文所提出的強非線性濾波方法實現對復雜場景中空間動目標的高精度協同跟蹤。本文給出如下假設:① 每部雷達僅接收自身回波信號;② 每部雷達不考慮位置誤差等。
假設在NRS中各部雷達同時發射信號,則第i部(1≤i≤N)雷達在k時刻的接收信號[1]表示如下:
式中:hi,k表示目標的RCS;αi,k為衰減因子,αi,k∝1/R4i,k,與目標到雷達的徑向距離Ri,k和天線增益等因素有關;Pi,k表示第i部雷達在k時刻的發射功率;si,k(t)為信號復包絡;τi表示回波時延。則可得到目標到雷達的徑向距離為
式中:c為光速。目標在k時刻的狀態可表示為xk=[xk,x·k,yk,y·k]T,且第i部雷達位置表示為(xrk)i=[(xrk)i,(yrk)i]T。fi(xk)表示在k時刻第i部雷達測量得到的多普勒頻移,可表示為
式中:λi和vi,k分別表示第i部雷達的波長及相對于目標的徑向速度。
1.2 運動模型
假設目標在空間中做NCV,則動態模型可表示為
式中:xk為目標狀態,xk=[xk,x·k,yk,y·k]T;Fk-1為狀態轉移矩陣;wk-1為過程噪聲,是均值為0方差為Qk-1的高斯白噪聲,可分別表示為
式中:U表示克羅內克積;I2表示2×2單位陣;q表示過程噪聲功率譜密度[16]。
1.3 量測模型
第i部雷達在k時刻的量測函數可表示為
式中:σri,k和σfi,k分別表示距離和多普勒頻移的量測噪聲,對應的噪聲協方差[23]分別為
式中:Bi,k和Ti,k分別表示第i部雷達在k時刻的有效帶寬和有效時間;SNRi,k表示第i部雷達在k時刻的回波信號的信噪比(signal-to-noise ratio, SNR),可表示為
由式(8)可知,雷達SNR取決于發射功率、徑向距離以及目標的RCS等因素,隨著功率的增加,雷達量測噪聲誤差減小。
則在k時刻2N個量測對應的量測噪聲協方差可表示為
本文中主要考慮在其他參數不變的情況下,功率與相對距離的函數關系,由式(9)可知,隨著功率增加,對應SNR增大,量測噪聲協方差降低;同理,隨著雷達與目標相對距離降低,SNR增大,量測對應噪聲協方差降低,測量精度增加。
2 基于PCRLB框架的組網雷達資源管理方法
NRS通過對多部雷達資源進行合理管理,包括在一定時間選擇最優雷達,或者對雷達進行優化布站等,實現組網雷達資源的最優管理。本文重點關注在雷達功率一定,或雷達能力受限情況下,通過優化選擇每個時刻的雷達資源,并結合本文所提出的高精度非線性點目標跟蹤算法,實現動目標狀態的精確跟蹤。
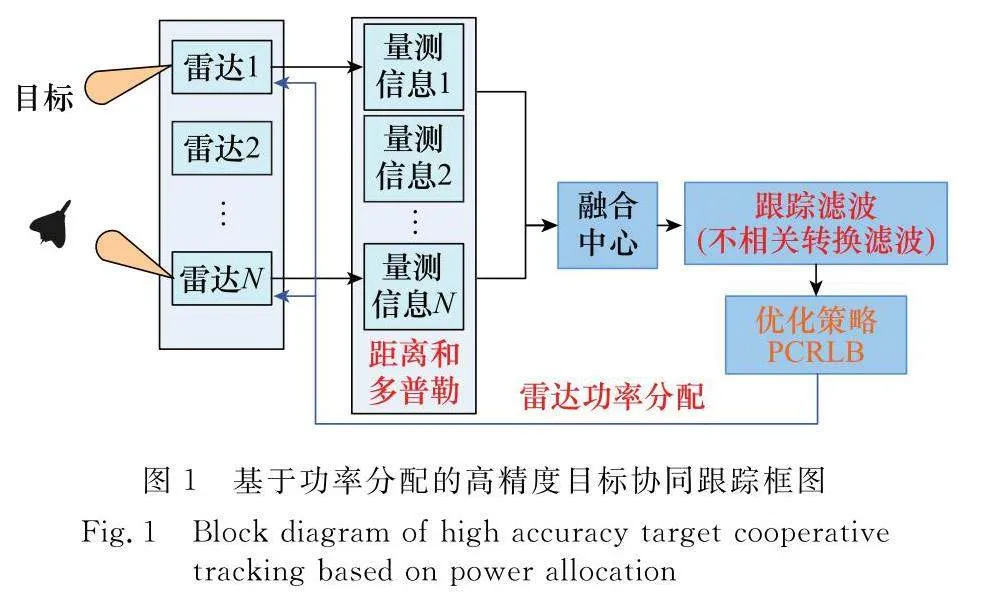
根據上述分析,本文考慮采用基于PCRLB的功率分配方法,利用PCRLB準則作為動目標跟蹤精度度量,在保證跟蹤精度最優的框架下,以跟蹤精度作為代價函數,實現組網雷達功率管理,得到最優的功率分配結果,并在此基礎上,利用本文所提出的非線性濾波方法,實現目標的精確跟蹤,具體框圖如圖1所示。
2.1 目標跟蹤中PCRLB框架
PCRLB可看作是對于非線性濾波問題的最好可實現的誤差性能度量,是無偏估計器最好均方誤差(mean square error, MSE)矩陣的一個下界[10,21],可表示如下:
式中:x^k為k時刻目標狀態估計量;Jk是k時刻的貝葉斯信息矩陣。在本文推導中,假設動態模型是線性的,量測模型為非線性,且噪聲都假設服從加性高斯。基于此,Jk的遞推計算[21]可簡化為
且Hk為量測函數的Jacobian矩陣(對雷達量測函數進行求導,并利用當前時刻的預測狀態進行求解),Rk=diag{QRk,Qfk}。則基于式(11),信息矩陣的遞推形式可進一步表示為
分析可知,Jd(xk)項只依賴于目標運動模型,與雷達具體信息無關;根據式(8)可知,Jz(xk)項與雷達發射功率、徑向距離和目標RCS等因素有關,特別是在其他因素不變的情況下,Jz(xk)項與雷達發射功率成正比。
對FIM求逆,即可得到下一時刻目標狀態的PCRLB,對應的MSE下界可表示為
該矩陣的對角線元素表征目標狀態各分量的預測方差下界,可精確衡量目標跟蹤精度,同時由于該矩陣是關于雷達發射功率的函數,因此可將式(14)進一步表示為下一時刻功率分配的代價函數:
式中:Pk=[P1,k,P2,k,…,PN,k]T表示k+1時刻中NRS中的全部雷達的發射功率集合;N為雷達個數。通過優化分配,令每部雷達發射合適的功率,實現跟蹤誤差的最小化,達到最佳跟蹤性能。
2.2 基于PCRLB的傳感器資源管理算法
由上述分析可知,目標的跟蹤精度與各部雷達位置、雷達發射功率及目標RCS等因素相關,本文主要討論雷達發射功率問題,在總功率一定的情況下,通過優化管理各部雷達發射功率,實現目標的精確跟蹤。因此,針對雷達功率分配的問題,可轉化為如下的優化問題:
式中:i=1,2,…,N,1T=[1,1,…,1]1×N;Pimin和Pimax分別表示第i部雷達發射功率的下限和上限。
根據文獻[6-7]可知,該優化問題可看作一個凸優化問題,利用凸優化函數進行求解,得到第i部雷達的功率分配Pi,k,利用該信息進行進一步狀態估計,并根據跟蹤結果計算下一時刻的PCRLB,從而修正下一時刻的功率分配,實現最優迭代。
具體求解步驟如下:式(16)的優化問題可看作一個半正定規劃(semi-definite programming, SDP)問題[24-25]。為了求解該SDP問題,引入一個輔助矩陣Mk,該矩陣需滿足如下約束:
因為FIM信息矩陣Jk為半正定矩陣,利用Schur補特性[4],式(17)形式可表示為
上述SDP優化問題可通過凸優化工具箱(convex optimization toolbox, CVX)等進行優化求解[4,24,26],得到每個時刻不同雷達的功率分配結果。
3 基于不相關轉換的非線性目標跟蹤方法
傳感器功率分配方法可根據具體的代價函數實現雷達布站、雷達發射功率及目標RCS等變量的最優分配,而在此基礎上要實現高精度動目標跟蹤,則面臨大噪聲、強非線性量測函數等難題。傳統的非線性濾波方法,即Kalman類濾波方法,包括EKF、UF、QKF等都屬于基于LMMSE框架下的線性結構濾波器,性能極大受限于其本身的線性結構,估計精度受到制約。
換言之,當量測為非線性,特別是強非線性時,量測與被估狀態為高度非線性關系,導致LMMSE估計器與量測的線性關系本質上失配,極大地限制了LMMSE框架及相關濾波器的估計性能,使其難以獲得高精度估計結果(LMMSE估計器只是線性估計器中的最優估計器),因此非線性估計精度有進一步提升的空間。
3.1 基于UCF的算法
為實現最佳的跟蹤精度,還需要考慮針對目標狀態估計的非線性濾波方法。鑒于此,本方案提出了一種基于UCF的算法,在得到功率分配結果后,利用發射功率提供的量測信息,通過該濾波方法進行目標狀態精確估計,實現機動目標的高精度跟蹤。
基于不相關轉換濾波器實質上是一種使用非線性轉換思想的擴維結構濾波器,通過利用非線性轉換對原始量測進行擴維,實現了性能的大幅提升。其中,轉換量測必須是原始量測的非線性函數,否則線性擴維將在LMMSE框架中失效(原因在于LMMSE估計器是最優的線性估計器)[16-17,21]。
當非線性轉換與原始量測不相關時,這類轉換稱為“不相關轉換”,得到的濾波器為基于UCF的濾波器,該濾波器是一種真正意義上的非線性濾波器,突破了現有LMMSE框架的線性結構,通過在更大空間尋優,從而提高非線性濾波精度。
采用原始量測的非線性轉換y=g(z)對原始量測進行擴維,可得到擴維后的量測形式:za=[zT,yT]T。則基于擴維量測,LMMSE框架[17]可重寫為如下形式:
狀態x^對應的MSE可表示為
由文獻[17]可知,式(22)等號右邊第二部分為正半定矩陣,因此使用擴維量測的LMMSE估計相比于原始的LMMSE估計,具有更小的MSE。
此外,為了得到一個通用的不相關轉換形式,文獻[17]進一步給出了如下一般性定理。
定理 1 如果z的分布p(z)關于均值z-對稱,且g(·)是一個偶函數(關于y軸對稱),則y=g(z-z-)滿足Pyz=0,則y是量測z的一個不相關轉換。(具體推導過程見文獻[17]推導過程)。
由上述推導,可利用問題特殊性構造出具體問題的不相關轉換形式,進而得到針對性的UCF算法,具體算法步驟如下。
步驟 1 狀態預測與量測預測
基于k-1時刻的x^k-1和Pk-1得到狀態預測x^k|k-1和對應的MSEPk|k-1。上述二階矩可利用無跡變換 (unscented transformation, UT) 或高斯厄米特求積(Gauss-Hermite quadrature, GHQ)準則等固定點采樣方法得到。同理,可獲得量測預測z^k|k-1和對應的MSE矩陣Pzk|k-1。基于前述信息,得到關于x^k|k-1和z^k|k-1的互協方差Pxzk。
步驟 2 構造擴維量測
基于z^k|k-1,Pzk|k-1和Pxzk等,構造不相關轉換量測yk=g(zk-z^k|k-1),本文中結合具體雷達量測(徑向距離和多普勒)函數,構建出具體的不相關轉換函數:
yk=g(zk-z^k|k-1)=(zk-z^k|k-1)T·(zk-z^k|k-1)(23)
其中,基于定理1可知,式(23)所構造的量測擴維項與原始量測不相關,即式(23)的不相關轉換形式可從原始量測中獲取更多的有效量測信息,從而在基于LMMSE濾波框架中,得到更精確的目標狀態前二階矩估計,提升目標跟蹤性能。
步驟 3 狀態更新
使用不相關轉換量測yk可得到擴維量測zak=[zTk,yTk]T,利用步驟1中的數值計算方法得到對應的擴維量測更新狀態z^ak=[z^Tk|k-1,y^Tk]T,互協方差Pxzak和協方差Pzak。而后基于LMMSE框架得到狀態估計x^k和對應的MSE矩陣Pk:
x^k=x^k|k-1+Pxzak(Pzak)-1(zak-z^ak)
Pk=Pk|k-1-Pxzak(Pzak)-1(Pxzak)T(24)
利用上述UCF算法,可實現強非線性濾波問題的精確求解,相比于原始LMMSE框架,量測中更多的有效信息可利用基于具體問題所構造的針對性不相關轉換獲取到,從而估計出更精確的前二階矩,具有更優的估計精度。
3.2 基于不相關轉換的組網雷達序貫濾波方法
組網雷達中的多傳感器同時獲取多組量測信息(徑向距離和多普勒信息),直接利用集中式融合中的并行濾波方法會導致非線性濾波方法中的組合量測維度過大,導致在利用固定點采樣方法,特別是采用GHQ采樣規則時出現維度爆炸(需mnx+nz個采樣點,其中nx和nz分別為目標狀態和組合量測維度,m為求積規則參數),對于UCF方法而言,擴維項的存在會進一步增加采點維度,導致計算復雜度增大,難以保證計算時效性。
為避免此類問題,本文提出基于不相關轉換的序貫濾波方法,采用多傳感器集中式序貫濾波方法進行多量測處理[20,27]。該算法核心思想如下:依次利用濾波方法處理多傳感系統中的每個傳感器量測數據。首先考慮對需要融合的多傳感數據進行時空配準,在此基礎上,使用UCF框架對第一個傳感器得到的量測信息進行濾波處理;將得到的目標狀態估計結果作為第二個傳感器的預測值,結合第二個傳感器的量測信息,在UCF框架中繼續估計出對應的狀態估計;以此類推,最后一個傳感器量測的序貫估計結果即為全部量測信息的融合目標狀態,濾波算法具體步驟如下(假設各傳感器在同一時刻之間量測噪聲互不相關)。
步驟 1 基于k-1時刻的目標前二階矩x^k-1和Pk-1得到狀態預測x^k|k-1和對應的MSE Pk|k-1。
步驟 2 使用傳感器1獲取的量測信息,利用上述所提出的UCF方法進行濾波。首先,通過z^k|k-1,Pzk|k-1和Pxzk等,構造具有與原始量測不相關特性的擴維項yk=g(zk-z^k|k-1),本文充分考慮雷達量測的特殊性,針對性提出一種擴維結構函數,基于提出的不相關轉換生成定理1,給出具體不相關轉換形式,即yk=g(zk-z^k|k-1)=(zk-z^k|k-1)T(·),該形式可保證盡可能多地提取原始量測中的有效信息;再將上述擴維量測信息通過UCF框架進行濾波,得到針對傳感器1的目標狀態估計x^1k|k和對應的MSE矩陣P1k|k。
步驟 3 將傳感器1處理得到的目標狀態前二階矩作為針對序貫處理傳感器2過程中的預測狀態及預測狀態協方差,即可分別表示為x^2k|k-1=x^1k|k,P2k|k-1=P1k|k。
步驟 4 利用不相關轉換擴維思想,得到傳感器2過程中的擴維量測,即(z2k)a=[(z2k)T,(y2k)T]T,基于UCF框架進行非線性濾波,得到對應的目標狀態前二階矩。以此類推,序貫處理全部傳感器之后,得到最終融合結果,即x^k|k=x^1~Nk|k,Pk|k=P1~Nk|k。
基于不相關轉換的組網雷達序貫濾波方法的具體算法流程如下。
步驟 1 融合中心對于目標狀態的一步預測:
x^k|k-1=Fk-1x^k-1
Pk|k-1=Fk-1Pk-1FTk-1+Gk-1Qk-1GTk-1(25)
步驟 2 針對傳感器1的狀態更新:
x^1k|k=x^k|k-1+K1~1k((z1k)a-(z-1k)a)
K1~1k=P1,xzak(P1,zak)-1
(P1k|k)a=Pk|k-1-P1,xzak(P1,zak)-1(P1,xzak)T(26)
步驟 3 針對傳感器1lt;i≤N的量測信息,序貫濾波狀態:
x^1~ik|k=x^1~i-1k|k+K1~ik((zik)a-(z-ik)a)
K1~ik=P1~i,xzak(P1~i,zak)-1
(P1~ik|k)a=P1~i-1k|k-1-P1~i,xzak(P1~i,zak)-1(P1~i,xzak)T(27)
步驟 4 序貫融合最終目標狀態估計結果:
x^k|k=x^1~Nk|k
Pk|k=P1~Nk|k(28)
該算法屬于集中式融合方法,可保證提供最優的融合性能,同時該思想已證明與并行濾波算法估計精度相同[20],可有效避免狀態維度過高導致的矩陣計算問題。此外,在具體的濾波算法中,針對量測函數的高度非線性,通過構造具體的不相關轉換形式,得到有效的擴維量測,并使用UCF框架可高效提取原始量測中的有效信息,從而實現目標狀態的高精度估計。
4 仿真驗證及分析
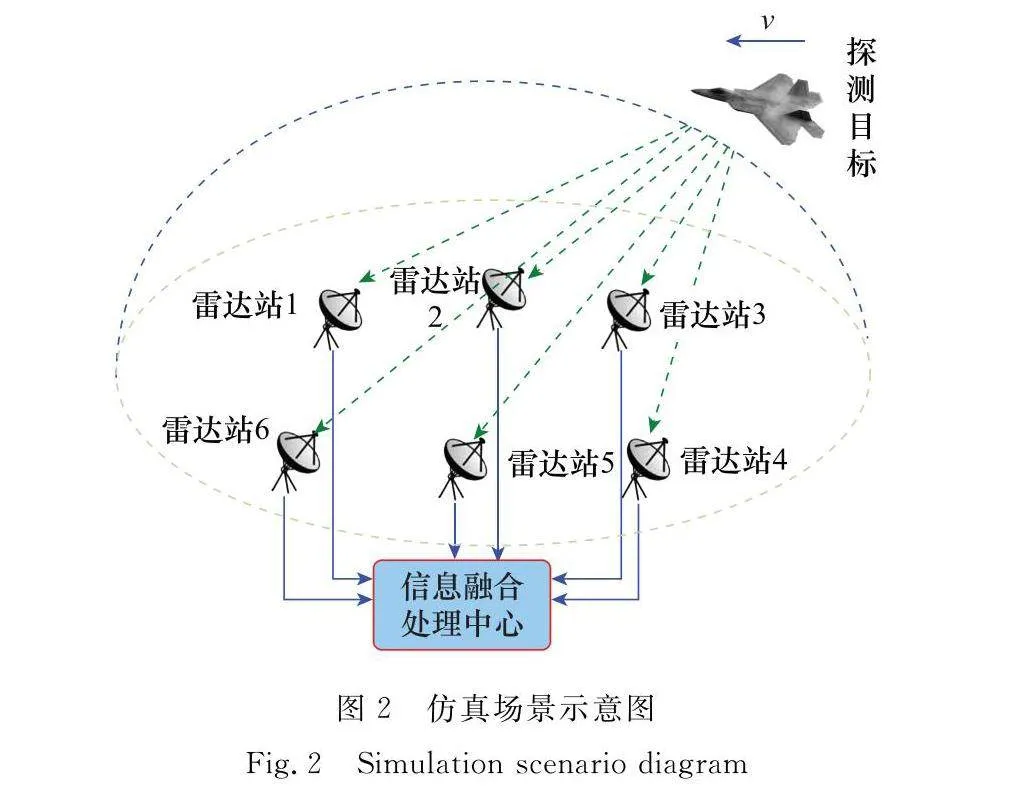
為驗證算法的有效性,本文考慮如下仿真場景:二維空間中一個目標作近似勻速直線或勻轉彎運動,初始位置為(10,0)km;其中,各部雷達發射信號參數相同,采樣間隔為5 s,采樣幀數為20。本次仿真比較了包括UF和UCF等濾波方法的均方根誤差(root mean square error, RMSE),蒙特卡羅次數為100,仿真場景示意圖如圖2所示。
采用兩種不同雷達布站方式如下。
(1) 使用4部雷達對動目標進行組網跟蹤,假設在20 km處,量測誤差方差分別為σ2r=200,σ2f=100。
(2) 使用6部雷達對目標進行組網跟蹤。假設在40 km處,量測誤差方差分別為σ2r=300,σ2f=100。各傳感器功率上下限分別為Pimax=0.6Ptotal,Pimin=Ptotal/100。
4.1 仿真驗證
(1) 場景1
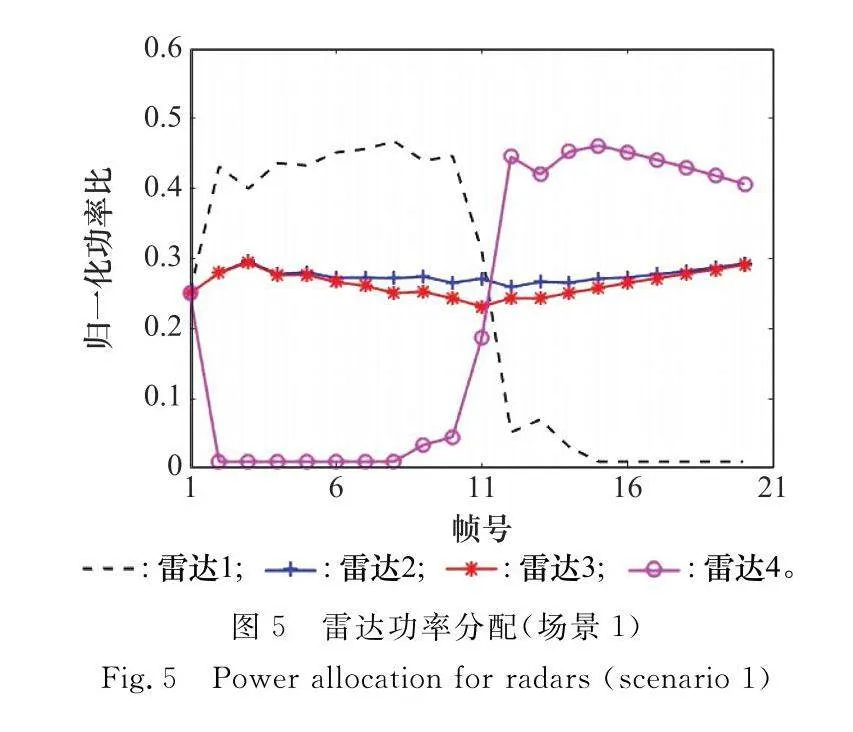
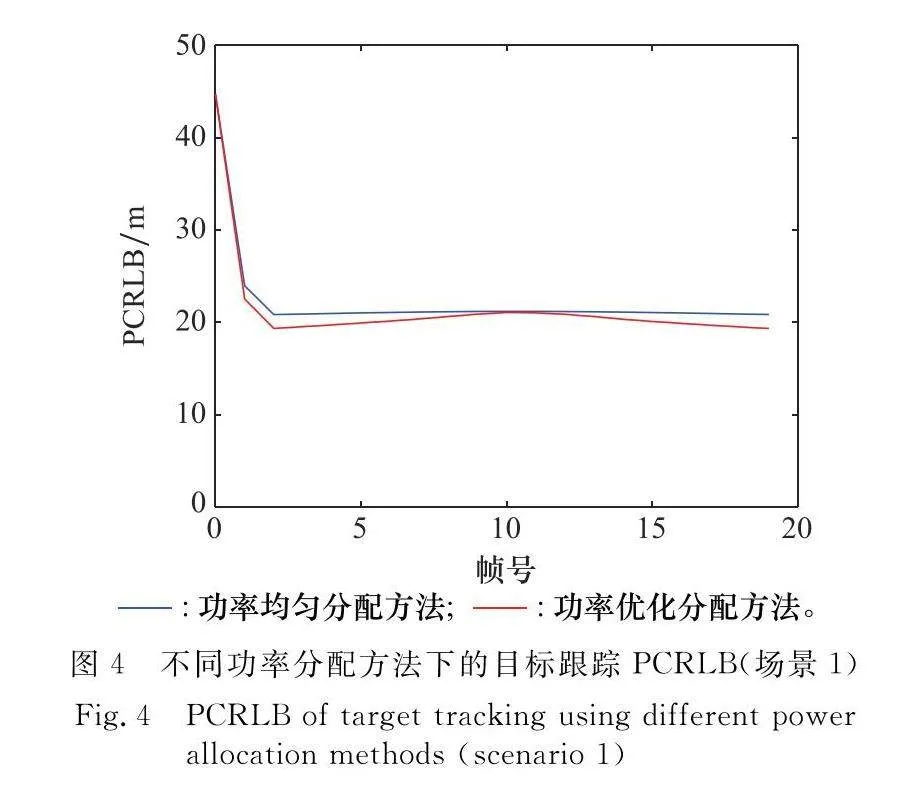
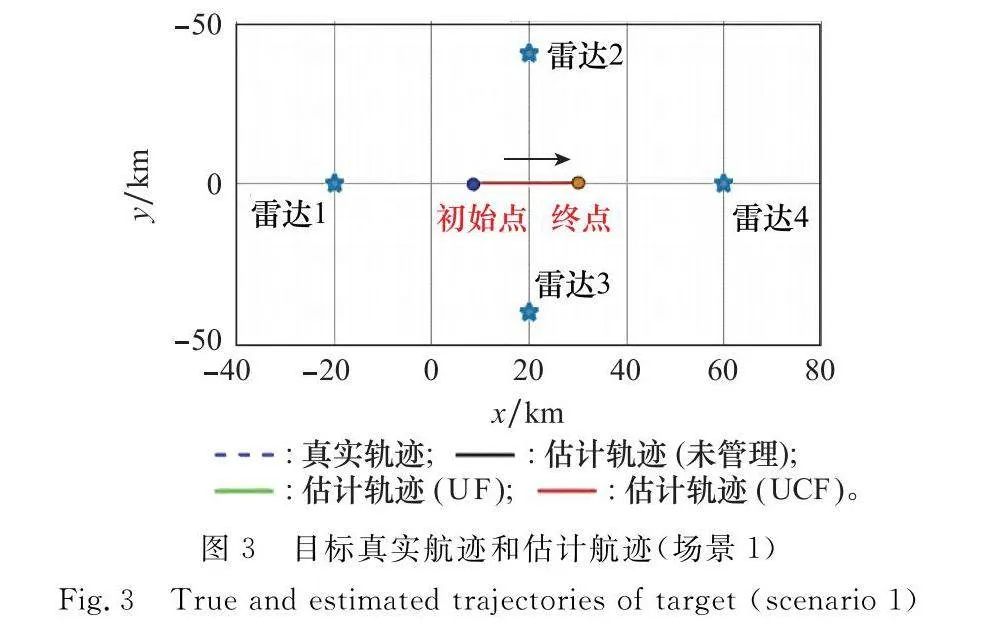
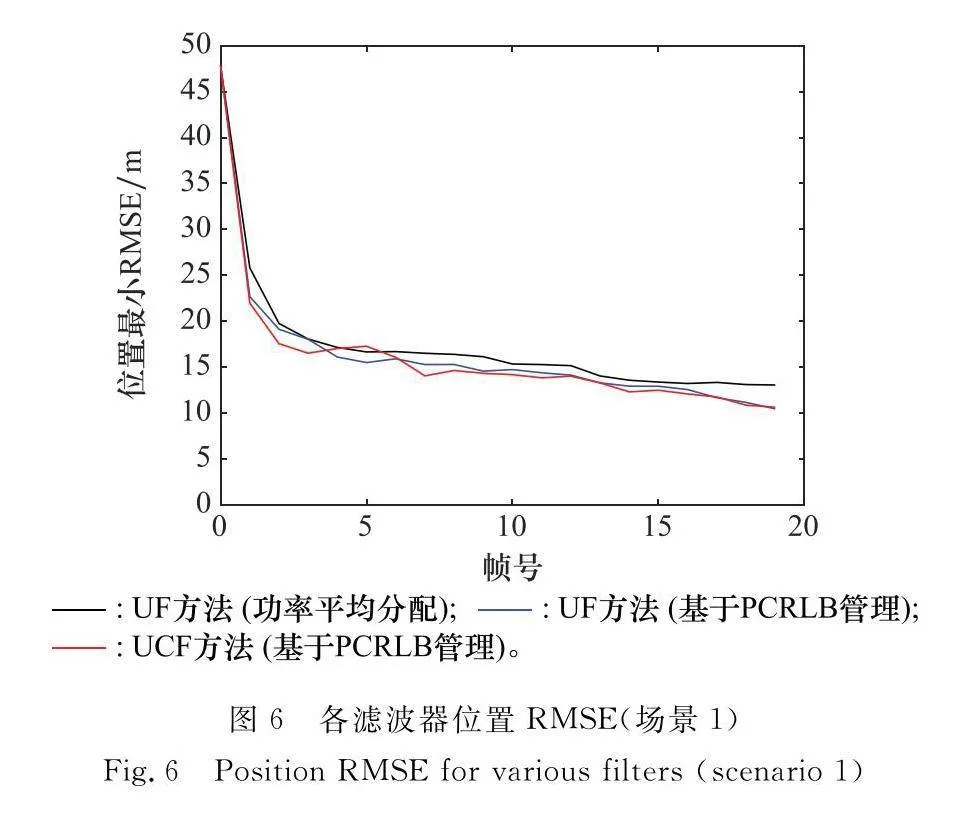
場景中目標運動速度為(200,0)m/s,布置4部雷達進行功率分配和目標跟蹤仿真驗證,各雷達布站參數如表1所示,目標真實航跡和各濾波方法得到的估計航跡如圖3所示,其仿真結果的進一步分析如圖4~圖6所示。
(2) 場景2
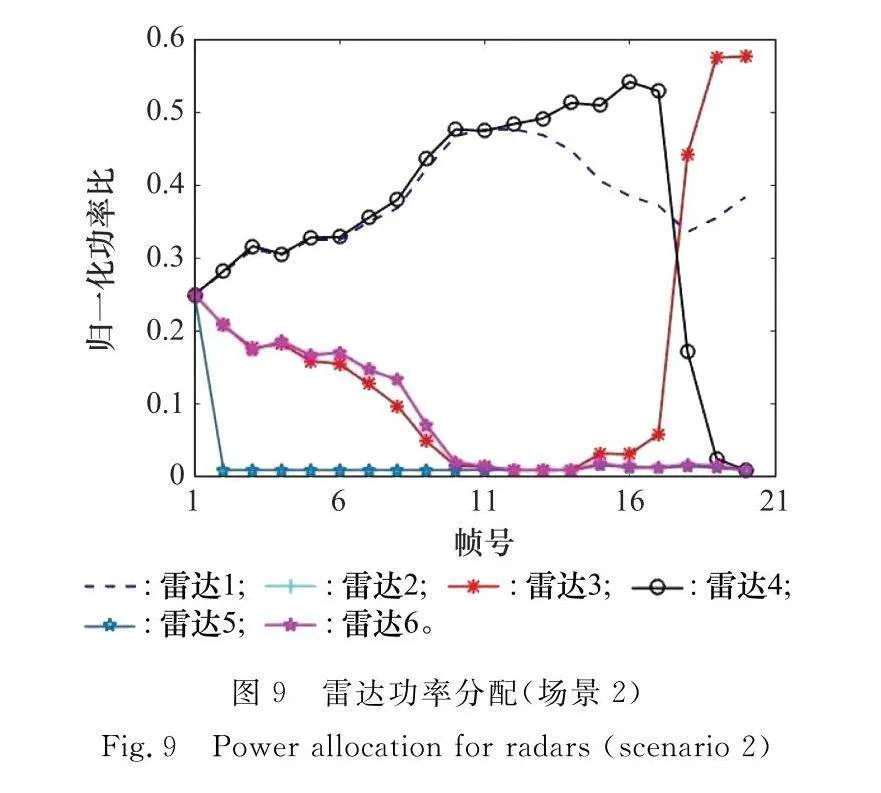
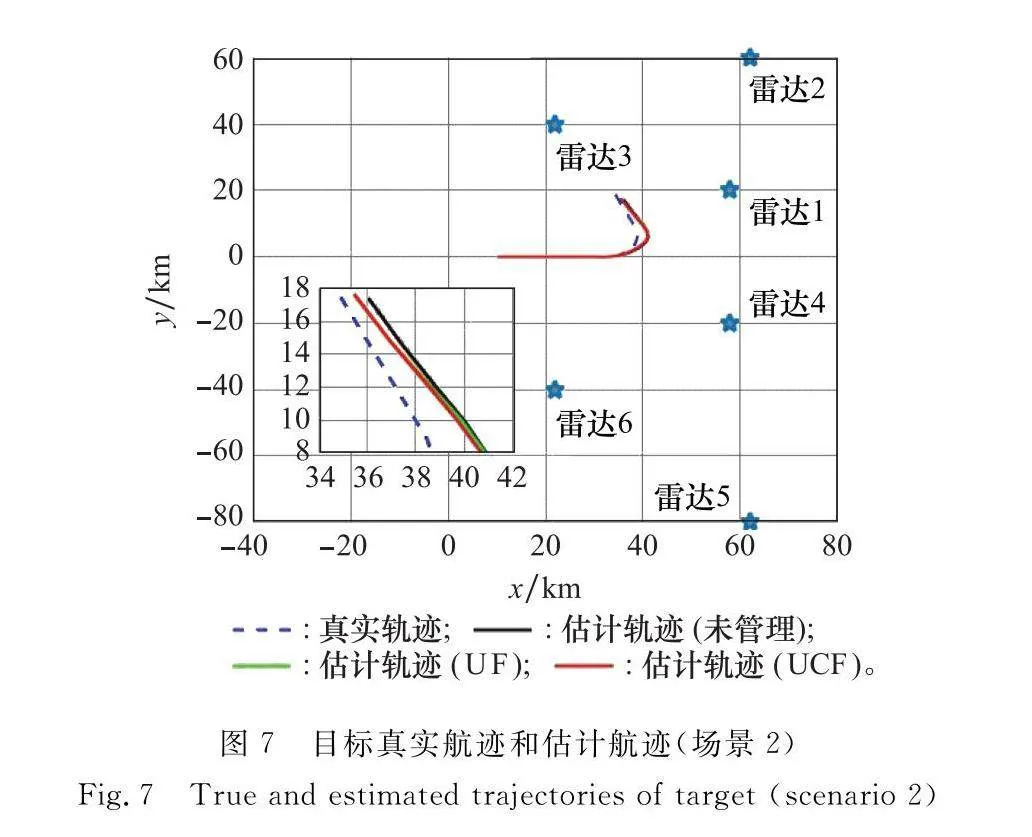
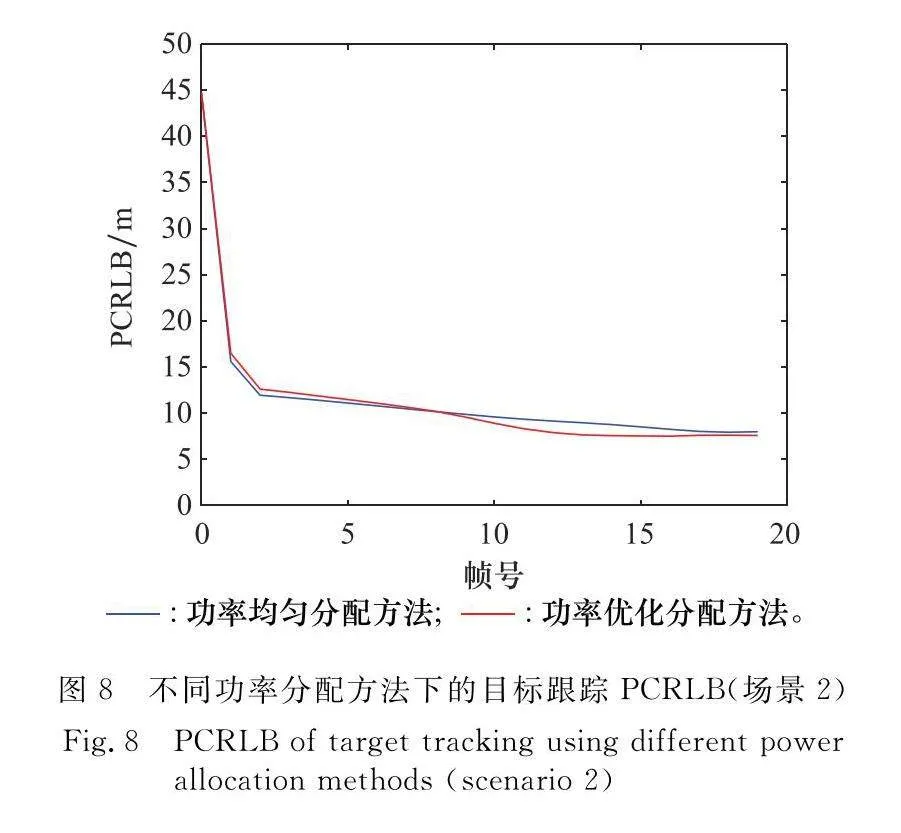
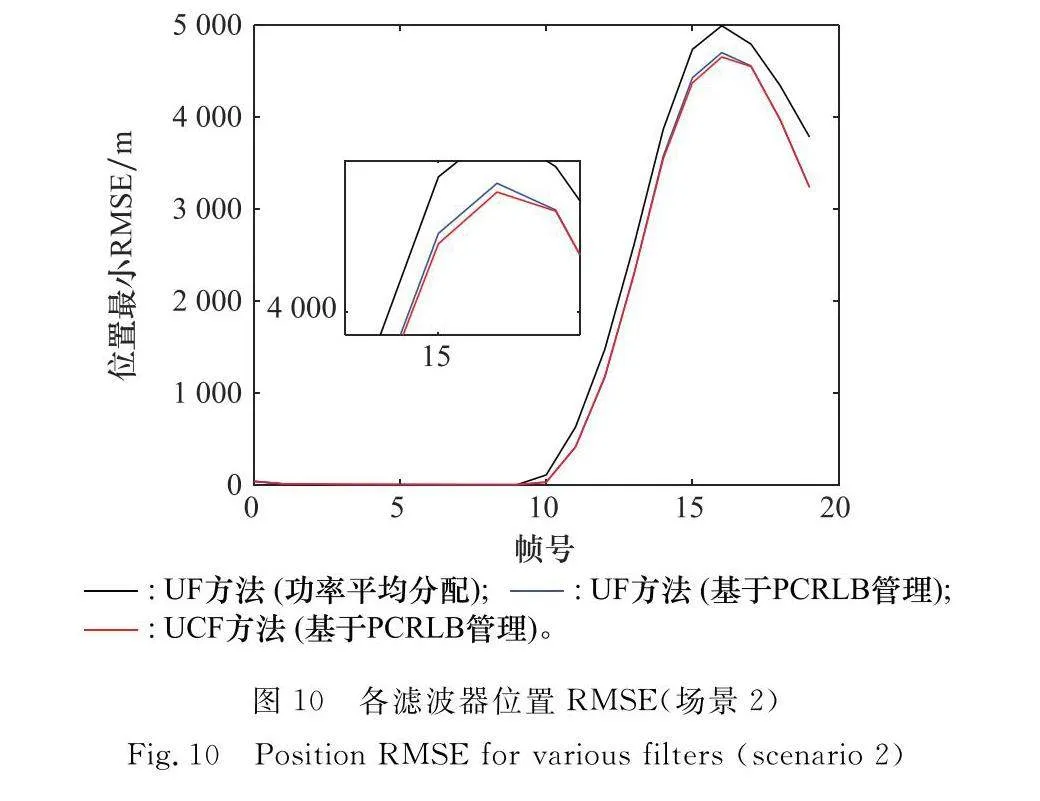
場景中目標運動速度為(500,0)m/s,先做勻速直線運動,而后進行勻轉彎運動,最后進行勻速直線運動。布置6部雷達進行功率分配和目標跟蹤仿真驗證,各雷達布站參數如表2所示,目標真實航跡和各濾波方法得到的估計航跡如圖7所示,其仿真結果的進一步分析如圖8~圖10所示。
4.2 仿真分析
(1) 由圖4和圖8分析可知,利用PCRLB度量準則的功率優化方法相比于功率均勻分配的方法而言,具有更好的跟蹤精度,具體原因:在總功率一定的情況下,以最小化PCRLB為優化函數,可得到當前時刻每部雷達的最優功率分配,從而獲取每部雷達的量測精度,保證了目標跟蹤的理論最優下界。此外,在場景1中,目標運動到10幀附近時,目標距離各雷達相對位置近似相等,此時功率均勻分配,兩種分配方案近乎相同,如圖4所示。
(2) 由圖5和圖9分析可知,在其他參數不變的情況下,基于PCRLB的功率分配方法與目標和雷達的相對距離有關,具體可參考式(8)。如圖5所示,雷達1在10幀之前,距離目標相對較近,分配較多功率,隨著目標運動,在與4部雷達距離近似相等時,功率分配基本一致,在10幀之后,目標距離雷達4較近,分配較多功率,上述趨勢與圖4中目標跟蹤PCRLB結論一致。如圖9所示,隨著目標進行轉彎運動,雷達3和雷達1相對位置更好,分配更多功率,而雷達4則由于遠離目標,功率分配顯著下降。
(3) 圖6和圖10分別表示不同場景中,不同功率分配方法下的目標跟蹤精度,以及在基于PCRLB方法下的不同非線性濾波方法跟蹤精度。重點分析UF方法和UCF方法可知,本文所提出的針對性擴維濾波UCF在大噪聲強非線性濾波問題中,具有更好的估計精度,主要原因在于:通過分析原始雷達量測函數(徑向距離和多普勒),利用問題特殊性,構建出具體的不相關轉換擴維量測,如式(23)所示,可有效提取原始量測中的更多信息,并將其應用于LMMSE濾波框架中,即UCF中,從而得到更高精度的目標狀態估計結果。由圖6和圖10結果可知,本文所提UCF方法可有效克服傳統濾波方法(如UF、QKF等)的性能缺陷,有效解決強非線性濾波問題。此外,該估計結果可反饋至功率分配方法中,實現更準確的功率分配,實現整體系統的優化求解。
5 結 論
針對組網雷達等體系化探測跟蹤系統,本文提出了一種基于UCF的目標協同跟蹤和功率分配方法,該濾波方法可通過所設計的針對性量測擴維項,有效提取原始量測中的更多信息,突破了傳統非線性濾波方法的本質缺陷,從而進一步在基于LMMSE的濾波框架中提高狀態估計性能。同時,高精度的狀態估計結果可用于基于PCRLB的功率分配方法中,高效準確分配當前時刻的各雷達功率,保證了NRS功率分配的優越性。
通過仿真可進一步驗證,利用非線性函數的特殊性,可構造出高效的不相關轉換擴維項,進而改善整體系統跟蹤和功率分配性能。本文所提不相關轉換具體構型只是眾多不相關轉換選擇中較好的一種,通過深入分析,可進一步構造出性能優異的不相關轉換擴維項。此外,分析UCF方法特性可知,對于大機動強非線性目標跟蹤問題,該方法相比于其他非線性處理方法優越性可能更加顯著。
參考文獻
[1]YAN J K, LIU H W, PU W Q, et al. Joint threshold adjustment and power allocation for cognitive target tracking in asynchr-onous radar network[J]. IEEE Trans.on Signal Processing, 2017, 65(12): 3094-3106.
[2]SUN H, LI M, ZUO L, et al. Joint threshold optimization and power allocation of cognitive radar network for target tracking in clutter[J]. Signal Processing, 2020, 172: 107566.
[3]時晨光, 丁琳濤, 汪飛, 等. 面向射頻隱身的組網雷達多目標跟蹤下射頻輻射資源優化分配算法[J]. 電子與信息學報, 2021, 43(3): 539-546.
SHI C G, DIND L T, WANG F, et al. Radio frequency stealth-based optimal radio frequency resource allocation algorithm for multiple-target tracking in radar network[J]. Journal of Electronics amp; Information Technology, 2021, 43(3): 539-546.
[4]XIE M C, YI W, KIRUBARAJAN T, et al. Joint node selection and power allocation strategy for multitarget tracking in decentralized radar networks[J]. IEEE Trans.on Signal Processing, 2018, 66(3): 729-743.
[5]SUN H, LI M, ZUO L, et al. Resource allocation for multitarget tracking and data reduction in radar network with sensor location uncertainty[J]. IEEE Trans.on Signal Processing, 2021, 69: 4843-4858.
[6]嚴俊坤. 認知雷達中的資源分配算法研究[D]. 西安: 西安電子科技大學, 2014.
YAN J K. Study on resource allocation scheme for cognitive radar[D]. Xi’an: Xidian University, 2014.
[7]嚴俊坤, 戴奉周, 秦童, 等. 一種針對目標三維跟蹤的多基地雷達系統功率分配算法[J]. 電子與信息學報, 2013, 35(4): 901-907.
YAN J K, DAI F Z, QIN T, et al. A power allocation approach for 3D target tracking in multistatic radar systems[J]. Journal of Electronics amp; Information Technology, 2013, 35(4): 901-907.
[8]俞曉波, 左燕, 郭寶峰, 等. 認知雷達網聯合傳感器選擇和功率分配[J]. 火力與指揮控制, 2018, 43(10): 57-62, 67.
YU X B, ZUO Y, GUO B F, et al. Joint sensor selection and power allocation in cognitive radar systems[J]. Fire Control amp; Command Control, 2018, 43(10): 57-62, 67.
[9]俞曉波. 多雷達系統協同跟蹤下資源分配[D]. 杭州: 杭州電子科技大學, 2018.
YU X B. Research on sensor resource management for multi-radar collaborative tracking system[D]. Hangzhou: Hangzhou Dianzi University, 2018.
[10]RISTIC B, ARULAMPALAM S, GORDON N. Beyond the Kalman filter: particle filters for tracking applications[M]. London: Artech House, 2003.
[11]李艷艷, 蘇濤. 機動目標跟蹤的分布式MIMO雷達資源分配算法[J]. 西安電子科技大學學報, 2016, 43(4): 10-16.
LI Y Y, SU T. Resource allocation approach for maneuvering target tracking in distributed MIMO radar systems[J]. Journal of Xidian University, 2016, 43(4): 10-16.
[12]時晨光, 王奕杰, 代向榮, 等. 面向目標跟蹤的機載組網雷達輻射參數與航跡規劃聯合優化算法[J]. 雷達學報, 2022, 11(5): 778-793.
SHI C G, WANG Y J, DAI X R, et al. Joint transmit resources and trajectory planning for target tracking in airborne radar networks[J]. Journal of Radars, 2022, 11(5): 778-793.
[13]孫揚, 鄭娜娥, 李玉翔, 等. 針對目標跟蹤的分布式MIMO雷達資源分配算法[J]. 系統工程與電子技術, 2017, 39(8): 1744-1750.
SUN Y, ZHENG N E, LI Y X, et al. Distributed MIMO radar resource allocation approach for target tracking[J]. Systems Engineering and Electronics, 2017, 39(8): 1744-1750.
[14]GODRICH H, PETROPULU A, POOR H V. Power allocation strategies for target localization in distributed multiple-radar architectures[J]. IEEE Trans.on Signal Processing, 2011, 59(7): 3226-3240.
[15]ZHANG H W, XIE J W, SHI J P, et al. Joint beam and waveform selection for the MIMO radar target tracking[J]. Signal Processing, 2019, 156(5): 31-40.
[16]LI X R, JILKOV V P. A survey of maneuvering target tracking: approximation techniques for nonlinear filtering[C]∥Proc.of the SPIE Conference on Signal and Data Processing of Small Targets, 2004: 537-550.
[17]LAN J, LI X R. Nonlinear estimation by LMMSE-based estimation with optimized uncorrelated augmentation[J]. IEEE Trans.on Signal Processing, 2015, 63(16): 4270-4283.
[18]LAN J, LI X R. Nonlinear estimation based on conversion-sample optimization[J]. Automatica, 2020, 121: 109160.
[19]LAN J, LI X R. Nonlinear estimation by linear estimation with augmentation of uncorrelated conversion[C]∥Proc.of the 17th International Conference on Information Fusion, 2014: 1-8.
[20]韓崇昭, 朱洪艷, 段戰勝. 多源信息融合[M]. 第2 版. 北京: 清華大學出版社, 2010.
HAN C Z, ZHU H Y, DUAN Z S. Multi-source information fusion[M]. 2nd ed. Beijing: Tsinghua University Press, 2010.
[21]ZHANG Y J, LAN J, MALLICK M, et al. Bearings-only filtering using uncorrelated conversion based filters[J]. IEEE Trans.on Aerospace and Electronic Systems, 2021, 57(2): 882-896.
[22]ZHANG Y J, LAN J. Gaussian sum filtering using uncorrelated conversion for nonlinear estimation[C]∥Proc.of the 20th International Conference on Information Fusion, 2017: 1297-1304.
[23]HAN Q H, PAN M H, LIANG Z H. Joint power and beam allocation of opportunistic array radar for multiple target tracking in clutter[J]. Digital Signal Processing, 2018, 78: 136-151.
[24]BOYD S, VANDENBERGHE L. Convex optimization[M]. New York: Cambridge University Press, 2004.
[25]LI X T, ZHANG T X, KONG L J, et al. Radar selection based on the measurement information and the measurement compensation for target tracking in radar network[J]. IEEE Sensors Journal, 2019, 19(18): 7923-7935.
[26]GRANT M, BOYD S. CVX: MATLAB software for disciplined convex programming, Version 1.21[EB/OL]. [2012-10-10]. http:∥cvxr.com/cvx.
[27]彭瀚, 程婷. 基于預測信息的量測轉換序貫濾波目標跟蹤[J]. 系統工程與電子技術, 2019, 41(3): 549-554.
PENG H, CHENG T. Sequential filtering for target tracking based on the prediction position conditioned measurement conversion[J]. Systems Engineering and Electronics, 2019, 41(3): 549-554.
作者簡介
張英杰(1991—),男,工程師,博士,主要研究方向為目標信息融合、組網雷達資源分配。
陳洪猛(1986—),男,高級工程師,博士,主要研究方向為雷達系統總體設計。
高文權(1981—),男,研究員,碩士,主要研究方向為雷達系統總體設計。
蘭 劍(1983—),男,教授,博士,主要研究方向為信息融合、目標跟蹤、性能評估。
葉春茂(1981—),男,研究員,博士,主要研究方向為雷達系統總體技術、雷達成像與識別。
陳 燕(1973—),女,研究員,博士,主要研究方向為雷達系統總體技術。

