基于彈性面域特性的虛擬管道優(yōu)化與設(shè)計

摘要： 針對集群路徑規(guī)劃中的運算量大、擁堵和碰撞等造成非彈性虛擬管道可行域受限的問題，提出一種基于彈性面域特性的虛擬管道模型。首先，提出彈性面域的概念，其彈性有界平面可作為虛擬管道的邊界，能夠有效利用脊曲線橫截面附近的空余空間來改變可行域范圍。其次，以管道內(nèi)部空間的脊曲線為基準(zhǔn)擴展安全區(qū)域，改進路徑規(guī)劃算法以適用于彈性面域虛擬管道。最后，通過對比仿真實驗，驗證該模型及所提算法在不同環(huán)境下的適用性及優(yōu)越性。該研究對虛擬管道概念在集群路徑規(guī)劃領(lǐng)域中的推廣應(yīng)用具有一定的實用價值。

關(guān)鍵詞： 虛擬管道; 彈性面域; A*算法; 貝塞爾曲線; 路徑規(guī)劃

中圖分類號： TP 301.6

文獻標(biāo)志碼： A

DOI：10.12305/j.issn.1001-506X.2024.11.28

Optimization and design of virtual tube based on elastic area characteristics

WU Yinfei， LI Xinkai^*， ZHANG Hongli， CHEN Yingying， GONG Fengjin

（School of Electrical Engineering， Xinjiang University， Urumqi 830017， China）

Abstract： In view of the problem that the feasible domain of inelastic virtual tube is limited due to the large amount of computation， congestion and collision in cluster path planning， a virtual tube model based on elastic area is proposed. Firstly， the concept of elastic area is proposed， the elastic bounded plane can be used as the boundary of the virtual tube， and can effectively use the free space near the cross section of the ridge curve to change the scope of the feasible region. Secondly， the safety zone is extended based on the ridge curve of the inner space of the tube， and a path planning algorithm is improved to apply to the elastic area virtual tube. Finally， through comparative simulation experiments， the applicability and superiority of the model and the proposed algorithm in different environments are verified. This study has certain practical value for the application of virtual tube concept in cluster path planning.

Keywords： virtual tube; elastic area; A* algorithm; Bezier curve; path planning

0 引 言

近年來，隨著人工智能和控制技術(shù)的迅速發(fā)展，單智能體受限于個體能力，面對復(fù)雜工況時無法高效、全面完成指定任務(wù)^［1］。因此，為了提高整體系統(tǒng)的性能和應(yīng)對未知環(huán)境的挑戰(zhàn)，將多個智能體進行有效協(xié)作和互動組成集群系統(tǒng)。由于集群系統(tǒng)的復(fù)雜性，多智能體如何快速穿越障礙物密集環(huán)境成了現(xiàn)代社會中一個重要且具有挑戰(zhàn)性的問題^［2］。而集群路徑規(guī)劃是集群系統(tǒng)中基礎(chǔ)且必需的部分，尤其對于無人機這類高自由度、高動態(tài)節(jié)點的智能體，其重要性不言而喻。

集群路徑規(guī)劃旨在有效地規(guī)劃和優(yōu)化多個智能體（如機器人、車輛或飛行器等）在給定環(huán)境下的路徑曲線，以實現(xiàn)任務(wù)目標(biāo)的同時避免碰撞、提高效率和保障安全性^［3-4］。目前，常用的集群路徑規(guī)劃方法歸類有集中式方法^［5-6］、分布式方法^［7-9］、基于機器學(xué)習(xí)的方法^［10-12］和混合式方法^［13-14］。集中式方法只適用于小規(guī)模集群，能夠?qū)崿F(xiàn)全局優(yōu)化，對于大規(guī)模集群會面臨計算復(fù)雜度和通信開銷的問題，且不夠靈活^［15］，如集中式優(yōu)化算法^［16］、相對安全走廊^［17］等;分布式方法具有較強的適應(yīng)性和魯棒性，能夠應(yīng)對部分信息缺失和多智能體之間的通信限制^［18］，然而不同智能體之間存在合作沖突，即各自追求個體利益而無法達成全局最優(yōu)解，如常用的算法包括勢場方法^［6］、群體智能^［19］、分布式搜索算法^［20］等。

現(xiàn)階段集群路徑規(guī)劃常用的仍然是單獨規(guī)劃所有智能體路徑，從而使多智能體成功抵達目的地的過程中避免撞到障礙物。這類方法耗時長、計算量大，需要大量通訊帶寬作為代價等缺陷。為解決復(fù)雜環(huán)境下的路徑規(guī)劃問題，有學(xué)者提出安全飛行走廊規(guī)劃方法^［21］，該類方法通過生成一條無障礙物的飛行區(qū)域來約束智能體的安全飛行，使得最優(yōu)控制問題的規(guī)模完全獨立于環(huán)境的復(fù)雜性，從而提高路徑規(guī)劃的速度。然而，該方法沒有考慮到三維空間中的大規(guī)模集群快速通行情況，飛行走廊通過凸規(guī)劃出的區(qū)域并不都適用于多智能體的通行，其擁有死角、尖點等阻塞多智能體通行的不規(guī)則區(qū)域。為此，近期有學(xué)者提出基于虛擬管道的集群飛行概念及規(guī)劃方法^［22-24］，該方法的概念與安全走廊類似，均可為智能體統(tǒng)一規(guī)劃出無障礙物的安全區(qū)域。其區(qū)別在于虛擬管道不僅為智能體提供安全可行路徑，且管道內(nèi)均是可行域。虛擬管道能夠同時為多智能體提供前進方向，且因其具有邊界光滑的特性更加適用于大規(guī)模集群快速通行。

正則虛擬管道^［22］方法能夠通過分布式集群路徑規(guī)劃的方法在規(guī)劃好的虛擬管道內(nèi)進行多智能體穿越。該方法相比于其他集群路徑規(guī)劃，離線規(guī)劃時虛擬管道的集群路徑規(guī)劃計算量更小，其他集群路徑規(guī)劃由多個循環(huán)執(zhí)行，而虛擬管道只執(zhí)行一次;且對于多智能體而言，只需要共享一個虛擬管道和相對位置即可安全通行，可以不用占據(jù)無線帶寬，這些優(yōu)點可顯著降低計算復(fù)雜度。然而，在高度復(fù)雜的環(huán)境中構(gòu)建虛擬管道時，容易出現(xiàn)空間利用率不足的問題。如面對非規(guī)則可行域時，虛擬管道的半徑僅按照可行域中最小可行半徑進行規(guī)劃，忽視了其他方位可利用空間，減少了多智能體通行數(shù)量，增加了多智能體集群抵達任務(wù)地點的時間。因此，本文針對這一問題提出一種改進的虛擬管道規(guī)劃方法，該方法規(guī)劃的虛擬管道稱為彈性面域虛擬管道，對非彈性面域虛擬管道規(guī)劃中空間利用率不足的情況進行優(yōu)化。

考慮彈性面域虛擬管道內(nèi)存在無數(shù)條可行路徑的情況，需要在規(guī)劃彈性面域虛擬管道主干脊曲線時，盡量避免與障礙物邊界或頂點重合，以確保脊曲線橫截面附近有足夠的規(guī)劃空間。A*算法^［25］作為路徑規(guī)劃算法中經(jīng)典的搜索方法，能夠在全局規(guī)劃中一次性找到全局最優(yōu)解，故本文以A*算法為例進行彈性面域虛擬管道脊曲線的規(guī)劃，以尋找最短路徑，并對其規(guī)劃路徑方法中容易與障礙物頂點相遇的不足進行改進，以滿足彈性面域虛擬管道的規(guī)劃需求。

本文的主要工作歸納如下：

（1） 本文提出的基于彈性面域特性的虛擬管道可以通過主副雙變軸共同規(guī)劃虛擬管道可行區(qū)域，提升虛擬管道的最大橫截面積與管道體積，有效降低多智能體在虛擬管道內(nèi)穿越總時長，提高可行區(qū)域;

（2） 本文在虛擬管道基礎(chǔ)上對彈性面域虛擬管道的定義進行補充，限制主軸在三維空間中的相對角度，并進行數(shù)學(xué)建模及系統(tǒng)分析;

（3） 為使彈性面域虛擬管道內(nèi)部空間能以脊曲線為基準(zhǔn)擴展安全區(qū)域，避免脊曲線與柵格障礙物頂點重合，對A*算法進行改進，以此適應(yīng)彈性面域虛擬管道的搭建，同時獲得起點和終點之間管道的最短管道路徑。

1 正則彈性面域虛擬管道的構(gòu)建

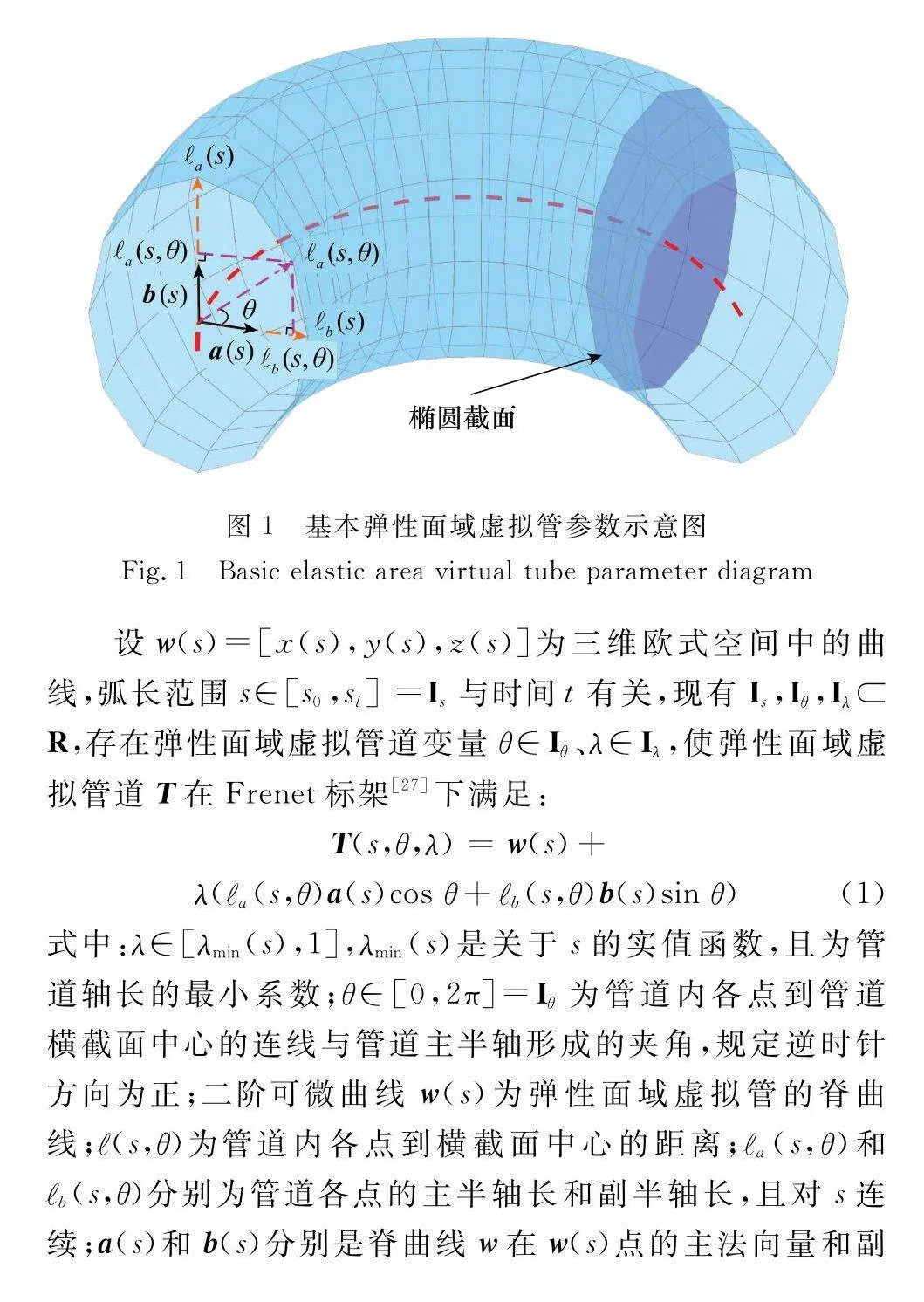
彈性面域虛擬管道由一條脊曲線和無數(shù)個垂直脊曲線的彈性有界平面組成。彈性有界平面可以根據(jù)環(huán)境狀況自適應(yīng)收放面積、扁窄度，從而改變可行域范圍，彈性有界平面的邊界作為彈性面域虛擬管道的邊界，約束管道內(nèi)智能體的通行范圍，將微分幾何^［26］融入該想法中，可得到一個基本彈性面域虛擬管道模型，如圖1所示。

設(shè)w（s）=［x（s），y（s），z（s）］為三維歐式空間中的曲線，弧長范圍s∈［s₀，s_l］=I_s與時間t有關(guān)，現(xiàn)有I_s，I_θ，I_λR，存在彈性面域虛擬管道變量θ∈I_θ、λ∈I_λ，使彈性面域虛擬管道T在Frenet標(biāo)架^［27］下滿足：

式中：λ∈［λ_min（s），1］，λ_min（s）是關(guān)于s的實值函數(shù)，且為管道軸長的最小系數(shù);θ∈［0，2π］=I_θ為管道內(nèi)各點到管道橫截面中心的連線與管道主半軸形成的夾角，規(guī)定逆時針方向為正;二階可微曲線w（s）為彈性面域虛擬管的脊曲線;?（s，θ）為管道內(nèi)各點到橫截面中心的距離;?_a（s，θ）和?_b（s，θ）分別為管道各點的主半軸長和副半軸長，且對s連續(xù);a（s）和b（s）分別是脊曲線w在w（s）點的主法向量和副法向量。

a（s）一般表達如下：

a（s）=w¨（s）w¨（s）（2）

由于三維曲線在某一點上的法向量并不唯一，且通過式（2）得到的主法向量a（s）繞w·（s）方向旋轉(zhuǎn)后仍為s點的主法向量。由于s是弧長，故w·（s）=［x·（s），y·（s），z·（s）］具有單位長度，引入其給定的切線指標(biāo)w：［0，l］→R³，較為方便理解a（s）的旋轉(zhuǎn)方式，如下所示：

a_r（s）=［x·（s），y·（s），0］·M_rx·（s）²+y·（s）²（3）

其中，旋轉(zhuǎn)矩陣M_r=［0，－1，0;1，0，0;0，0，1］，若a_r（s）=［0，0，0］，則a_r（s_i）=a_r（s_i－1）。

本文對旋轉(zhuǎn)后的a_r（s）進行約束限制，使其旋轉(zhuǎn)至滿足下列條件：

（1） 非弧長s起點處主法向量a_r（s）⊥［0，0，1］且a_r（s_i）·a_r（s_i－1）gt;0，i=1，2，…，l為弧長s采樣點標(biāo)號;

（2） 弧長s上起點s₀處主法向量a_r（s₀）需滿足a_r（s₀）⊥［0，0，1］且a_r（s₀）·［0，1，0］gt;0;

（3） 若弧長s上起點s₀處管道橫截面T（s₀，θ，λ）⊥［0，0，1］，即主法向量a_r（s₀）⊥［1，0，0］且a_r（s₀）⊥［0，1，0］，那么規(guī)定s₀處的主法向量a_r（s₀）=［0，1，0］。

b（s）如下所示：

b（s）=w·（s）w·（s）×a_r（s）（4）

為方便后文敘述，彈性面域虛擬管表面用T₁（s，θ）=T（s，θ，1）表示;彈性面域虛擬管T在點w（s₀）的橫截面用T_s0（θ，λ）=T（s₀，θ，λ）表示;彈性面域虛擬管T主半軸用?_a（s）=?（s，0°）表示，副半軸用?_b（s）=?（s，90°）表示。

定義 1 彈性面域虛擬管道的自交。如果彈性面域虛擬管橫截面T（s₁，θ₁，λ₁）內(nèi)存在另一組參數(shù)（s₂，θ₂，λ₂）對應(yīng)的管道面T（s₂，θ₂，λ₂），則彈性面域虛擬管道在w（s₁）點出現(xiàn)曲面自交區(qū)域，如下所示：

T_s1（θ₁，λ₁）=T_s2（θ₂，λ₂），s₁≠s₂（5）

自交有兩種不同的類型，一種是脊曲線上兩個距離較遠的點的橫截面相交造成的全局自交，另一種是脊曲線局部高曲率或主副軸長大于主副軸方向的曲率半徑造成的局部自交^［28］，如圖2所示。由于彈性面域虛擬管道曲面自交沒有具體明確的定義，因此本文對其進行自定義。

定義 2 彈性面域虛擬管道的局部自交。設(shè)彈性面域虛擬管道存在自交點為w（s₁），當(dāng)給定小數(shù)?εgt;0，有θ₁，θ₂∈I_θ，λ₁，λ₂∈I_λ，s₂∈R使下式成立：

|s₁－s₂|lt;εT_s1（θ₁，λ₁）=T_s2（θ₂，λ₂）（6）

那么在w（s₁）點處存在的自交為彈性面域虛擬管的局部自交;否則，自交集就是全局的自交集。

由于彈性面域虛擬管的主軸和副軸變化可能出現(xiàn)相互交換長度現(xiàn)象，故彈性面域虛擬管的橫截面收縮率定義為常規(guī)的體積或者橫截面積縮減率是不可行的。因此，本文在此定義彈性面域虛擬管的窄化率和扁化率，以此共同描述彈性面域虛擬管邊界的收縮率，避免主副軸長度交換但面積不變的情況。

定義 3 彈性面域虛擬管道的窄化率和扁化率。窄化率定義為彈性面域虛擬管主軸長度縮減速率;扁化率定義為彈性面域虛擬管副軸的長度縮短速率。

定義 4 彈性面域虛擬管道表面為正則曲面。若對彈性面域虛擬管道表面T₁（s，θ）所有點處都連續(xù)可微，且對于常數(shù)v₁，v₂使得

v₁?T₁?s+v₂?T₁?θ=0， s∈R;θ∈I_θ（7）

有唯一解為v₁=v₂=0，那么該彈性面域虛擬管表面是正則曲面。

定義 5 彈性面域虛擬管道的橫截面是單連通的。如果在T_s（θ，λ）中的每一個封閉環(huán)路都可以連續(xù)變換或收縮到T_s（θ，λ）內(nèi)的一點，則彈性面域虛擬管的橫截面T_s（θ，λ）是單連通的。

為了適應(yīng)多智能體的一般運動方式，本文提出的彈性面域虛擬管道同樣需要滿足類似文獻［22］中提出的4個構(gòu)建原則。

原則 1 彈性面域虛擬管道表面是正則的。

原則 2 彈性面域虛擬管道擁有比較低的窄化率和扁化率。

原則 3 彈性面域虛擬管道的橫截面是單連通的。

原則 4 彈性面域虛擬管道沒有自交。

在彈性面域虛擬管道的規(guī)劃階段，一個正則彈性面域虛擬管道應(yīng)該滿足上述4個原則。為此，本文對正則彈性面域虛擬管道的定義進一步完善。

定義 6 正則的彈性面域虛擬管道T（s，θ，λ）是具有最小收縮率η_min的彈性面域虛擬管道。若彈性面域虛擬管道窄化率和扁化率均滿足η_a，η_b≥η_min，管道表面光滑正則，其橫截面為單連通截面，且管內(nèi)無自交，則稱這類彈性面域虛擬管道為具有最小收縮率η_min的正則彈性面域虛擬管道。

2 正則彈性面域虛擬管道數(shù)學(xué)描述

2.1 正則曲面的彈性面域虛擬管道

若彈性面域虛擬管表面是正則曲面時，需要根據(jù)定義4，將式（1）代入式（7）得正則彈性面域虛擬管的約束條件^［22］，如下所示：

2.2 彈性面域虛擬管道的窄化率及扁化率

彈性面域虛擬管道中某一段的橫截面邊界驟然收縮會使多智能體穿越該段管道時出現(xiàn)阻塞現(xiàn)象，因此本文設(shè)定一個值來標(biāo)明彈性面域虛擬管的窄化強度和扁化強度，稱為彈性面域虛擬管的最小窄化率和最小扁化率。本文對彈性面域虛擬管的主副軸分別設(shè)置相同的窄化率及扁化率，使該管道是具有最小收縮率限定值的彈性面域虛擬管道，以此來表述定義4中的窄化率和扁化率及定義7中的收縮率。

根據(jù)兩點之間的距離公式，得到w（s₀）點的彈性面域虛擬管橫截面主軸和副軸的長度如下所示：

式中：L_a是主軸長度;L_b是副軸長度。因此，彈性面域虛擬管道的主軸窄化率及副軸扁化率為

窄化率和扁化率只存在于彈性面域虛擬管道主軸與副軸對應(yīng)兩端光滑可微時，否則彈性面域虛擬管道若為直管道時不存在窄化率和扁化率。

由式（12）和式（13）可知，|η_a|越大，管道表面變化越大，主軸的窄化率與?_a（s）和?_s有關(guān)，?_a（s）與|?_s|越大，η_a越大，當(dāng)η_agt;0時，彈性面域虛擬管變寬;同理，副軸的扁化率與?_b（s）和?_s有關(guān)，?_b（s）和|?_s|越大，η_b越大，當(dāng)η_bgt;0時，彈性面域虛擬管道被縱向拉伸。當(dāng)主軸與副軸均在拉伸時，彈性面域虛擬管道膨脹，多智能體不會被管道壁阻塞;當(dāng)η_alt;0或η_blt;0時，彈性面域虛擬管道左右兩側(cè)或上下兩側(cè)收縮，多智能體會因彈性面域虛擬管快速縮小出現(xiàn)阻塞，故限制η_a，η_b的最小值可以有效緩解管道內(nèi)阻塞現(xiàn)象。

2.3 單連通的彈性面域虛擬管道

為使彈性面域虛擬管是單連通管道，文獻［29］提出一種偏置曲線局部和全局自交剪裁算法，并拓展至可變偏置距離的情況，文獻［30］將其結(jié)果推廣到偏置曲面的局部自交和全局自交的一般情況。經(jīng)過大量學(xué)者實驗數(shù)據(jù)顯示和分析，虛擬管道單連通需要w·（s）的方向與?T₁（s，θ）/?s方向相同^［31］，如下所示：

彈性面域虛擬管表面T₁（s，θ）中?s和?θ均滿足式（14）中的約束，則其為彈性面域虛擬管中單連通的橫截面。若管道為單連通管道，則管道無局部自交^［22］，因此為方便計算，現(xiàn)將式（14）進一步簡化^［32］為

2.4 無自交現(xiàn)象的彈性面域虛擬管道

為了簡化約束條件和減少計算量，本文通過定義2中彈性面域虛擬管道自交的性質(zhì)，給出數(shù)學(xué)描述來簡化無自交管道規(guī)劃的過程。

對于規(guī)劃中出現(xiàn)全局自交的情況，可以在規(guī)劃彈性面域虛擬管道時，通過合理設(shè)置最大主副半軸長度和合理規(guī)劃環(huán)境中的脊曲線來解決。完成彈性面域虛擬管道規(guī)劃后，通過全局搜索來檢測是否存在全局自交。在實時彈性面域虛擬管道規(guī)劃中，由于多智能體只需要關(guān)注局部的彈性面域虛擬管模型，因此不需要考慮全局自交問題。

2.5 正則彈性面域虛擬管道的約束

本文規(guī)劃的彈性面域虛擬管道使用全局規(guī)劃生成脊曲線，因此主要考慮管道局部性質(zhì)，不考慮全局自交問題。若滿足上述4個原則，則可得到適合集群控制規(guī)劃的彈性面域虛擬管道，稱為正則彈性面域虛擬管道，如圖3（b）所示。從圖3（b）中可以看到，正則規(guī)劃后的彈性面域虛擬管道對圖3（a）中管道表面不規(guī)則、自交區(qū)域進行優(yōu)化，使其管道面無凸起、無阻塞點，這會更利于多智能體在管道內(nèi)的穿越。

對正則彈性面域虛擬管道的所有約束條件表達如下：

3 正則彈性面域虛擬管建模步驟

多智能體需要在彈性面域虛擬管道內(nèi)進行快速穿越，而管道壁則是多智能體可行區(qū)域約束邊界，故本節(jié)對彈性面域虛擬管道表面進行規(guī)劃即可。

規(guī)劃彈性面域虛擬管道表面總共分為兩個步驟，第1步先規(guī)劃彈性面域虛擬管道的脊曲線w（s），從而得出主法向量a（s）與副法向量b（s）;第2步根據(jù)第1步得到的脊曲線w（s）和兩個法向量a（s）、b（s）結(jié)合環(huán)境障礙物情況單獨規(guī)劃彈性面域虛擬管面主副雙變軸長?_a（s，θ）和?_b（s，θ）。

3.1 彈性面域虛擬管道脊曲線的規(guī)劃

脊曲線的規(guī)劃同樣分為兩個步驟。首先，利用尋徑算法生成從起點到終點的離散路徑點，其次對路徑點之間的軌跡進行連續(xù)平滑處理。

在設(shè)計彈性面域虛擬管道時，需要考慮管道內(nèi)存在無數(shù)條可行路徑，而不僅僅是單一可行路徑。因此，在規(guī)劃脊曲線時，需要避免與柵格障礙物頂點相交的問題，故本文對傳統(tǒng)的A*算法進行改進。相比于傳統(tǒng)A*算法追求最短路徑，該算法更加兼顧彈性面域虛擬管表面構(gòu)造要求。改進后的A*算法如下所示：

f*（n^）=g（n^）+h（n^）（17）

式中：f（n^）為節(jié)點n^的估價函數(shù)，表示從起點經(jīng)由節(jié)點n^到達終點的代價估計，其由起點到達節(jié)點n^的代價g（n^）和從節(jié)點n^到達終點的最短路徑的估計代價h（n^）組成。g（n^）采用歐氏距離法，其數(shù)學(xué)表達式如下所示：

g（n^）=P_start－P_n^（18）

式中：P_start表示脊曲線的起點位置;P_n^表示當(dāng)前節(jié)點位置。

A*算法中常用曼哈頓距離、切比雪夫距離和歐氏距離作為啟發(fā)函數(shù)進行計算。在三維柵格地圖中，彈性面域虛擬管需要最大限度地減少彎折頻率，減少多智能體脫離管道的情況。曼哈頓距離是通過計算兩點之間沿著網(wǎng)格線的距離來衡量的，在計算路徑時，只能朝上下前后左右6個方向計算;與之相對，歐氏距離可以在任意方向上移動;切比雪夫距離太過單一，通常適用于特定的用例。在考慮虛擬管道轉(zhuǎn)彎較少的情況下，曼哈頓距離更適合用于彈性面域虛擬管的脊曲線規(guī)劃。因此，本文采用曼哈頓距離來計算A*算法的啟發(fā)函數(shù)，以提高尋路效率，如下所示：

確定父節(jié)點n^后，子節(jié)點n^+1的三維空間選取序列如圖4所示。

從圖4中可以看到，本文對三維空間的柵格地圖進行分層規(guī)劃，共分為3層，從所在層開始遍歷，其次向上層遍歷，最后向下層遍歷。

非跨層子節(jié)點n^+1的選取及舍棄規(guī)則如圖5所示。圖5可視化展示子節(jié)點非跨層情況的選取情況，圖中黑色方塊為障礙物方塊，灰色方塊為封閉列表中的父節(jié)點n^－1，為已規(guī)劃后確認的路徑節(jié)點。若開放列表中的父節(jié)點n^與子節(jié)點n^+1之間的移動路徑與靜態(tài)障礙物邊界最短距離為0，則舍棄該子節(jié)點重新選取另一子節(jié)點。

三維空間中子節(jié)點的具體選取規(guī)則如表1所示。其選取方法參照二維平面上子節(jié)點的選取方法，若直線路徑過程中與障礙物邊界相交則該路徑不可取，并刪除該子節(jié)點。

對離散的路徑點進行平滑處理，本文采用貝塞爾曲線方法進行路徑平滑^［33］，如下所示：

b_j（t）=c⁰_jB⁰_n（t）+c¹_jB¹_n（t）+…+cⁿ_jBⁿ_n（t）=∑ni=0cⁱ_jBⁱ_n（t）（20）

式中：{c⁰_j，c¹_j，…，cⁿ_j}是第j段貝塞爾曲線的控制點集，記為c_j;n是貝塞爾曲線階次;Bⁱ_n（t）是伯恩斯坦多項式，如下所示：

式中：Q是該式的二次項系數(shù)矩陣;i=0，1，…，n。

根據(jù)式（20）和式（21）可得到分段三階貝塞爾函數(shù)平滑后的彈性面域虛擬管道脊曲線，如下所示：

式中：F（t）=［F_x（t），F(xiàn)_y（t），F(xiàn)_z（t）］^T表示規(guī)劃后曲線上的點在空間中的三維坐標(biāo);cⁱ_γj=［cⁱ_γj，x，cⁱ_γj，y，cⁱ_γj，z］^T表示貝塞爾分段曲線中的三維控制點。

對于每一段三階貝塞爾曲線，分段起點和分段終點分別與第1個控制點c⁰_j和第4個控制點c³_j重合，因此只要確定剩余2個控制點c¹_j、c²_j，就可得到每一段彈性面域虛擬管道的脊曲線。

為使分段貝塞爾曲線在連接處速度近似連續(xù)，故設(shè)置如下的連接點約束：

dc³_j（t）dt_t=tm=dc⁰_j+1（t）dt_t=tm，m=1，2，…，j－1（23）

本文為使平滑后的脊曲線更加適合彈性面域虛擬管道的建模，因此設(shè)置如下所示的目標(biāo)函數(shù)：

弧長s與時間t的關(guān)系為

s（t）=∫^t_t0|F·（t）|dt（25）

故由時間t規(guī)劃出一系列三維坐標(biāo)點F（t）可轉(zhuǎn)變?yōu)橐曰￠Ls為自變量的脊曲線w（s）。

3.2 彈性面域虛擬管道主副半軸的規(guī)劃

本節(jié)在第3.1節(jié)規(guī)劃出來的脊曲線基礎(chǔ)上，對彈性面域虛擬管道的主副半軸長進行規(guī)劃，主要目的是使彈性面域虛擬管道的橫截面積和最終生成的管道體積足夠大，從而方便多智能體集群的穿越。

為方便目標(biāo)函數(shù)的計算，在規(guī)劃彈性面域虛擬管道上各點的主副半軸長時，將其進行類似于式（22）分段式脊曲線的參數(shù)化。主半軸長和副半軸長參數(shù)分別如下所示：

式中：αⁱ_j（θ）=βⁱ_j（θ）=∑nk=0χⁱ_kθ^k表示第j段i階的主副半軸長系數(shù)，χⁱ_k表示第k段i階的系數(shù)。

由于所需彈性面域虛擬管道需要滿足多智能體穿越的4個原則，故規(guī)劃其可行域時需要主副半軸長最大化，且需要管道表面沒有較大起伏。為了全局規(guī)劃后的彈性面域虛擬管道不存在全局自交，因此需要對彈性面域虛擬管道的主副半軸長進行限制，設(shè)置最大主副半軸長分別為?_amax和?_{b max}。若最大半軸長內(nèi)沒有障礙物，則默認當(dāng)前規(guī)劃虛擬管道的半軸長為最大半軸長，如下所示：

式中：?_{a min，i}和?_{b min，i}分別為脊曲線的第i段與障礙物的最小主副半軸距離;i=1，2，…i_j。

結(jié)合式（28）中的障礙約束、式（16）中的正則彈性面域虛擬管道約束和式（23）中的連續(xù)約束優(yōu)化主副半軸長，將脊曲線w（s）與優(yōu)化后的主副半軸長?_a（s，θ）和?_b（s，θ）相結(jié)合，規(guī)劃出正則彈性面域虛擬管道。

設(shè)置主副軸代價函數(shù)為

規(guī)劃彈性面域虛擬管道的目標(biāo)函數(shù)為

約束條件為式（16）、式（23）和式（28）。

彈性面域虛擬管道完整的規(guī)劃過程如算法1所示。算法 1 正則彈性面域虛擬管道規(guī)劃步驟輸入：起點，終點，地圖，收縮率，管道最大半軸長輸出：w（s），?_a（s，θ），?_b（s，θ），n（s），b（s）1使用改進后的A*算法找到離散路徑點2

使用分段三階貝塞爾曲線優(yōu)化離散路徑點得出w（s），如式（22）、式（25）所示。3根據(jù)脊曲線w（s）得出n（s）和b（s）4for i≤j do5求w（s）到障礙物的最小距離?_{a min，i}和?_{b min，i}6if ?_{a min，i}gt;?_max then7 ?_{a min，i}=?_max8end9if ?_{b min，i}gt;?_max then10 ?_{b min，i}=?_max11end12end13優(yōu)化中加入障礙物約束、正則約束和連續(xù)約束14由式（26）和式（27）得主半軸?_a（s，θ）和副半軸?_b（s，θ）15T（s，θ）=w（s）+（?_a（s，θ）n（s）cos θ+?_b（s，θ）b（s）sin θ）

4 仿真結(jié)果

本節(jié)對所改進的彈性面域虛擬管道進行仿真，使用了配備Intel（R） Core i7-8750H處理器（主頻2.20 GHz）和16 GB內(nèi)存的電腦。本文使用二階智能體，采用文獻［34］中的控制器及參數(shù)模擬多智能體在彈性面域虛擬管內(nèi)進行穿越，選擇的仿真步長為0.01 s。

4.1 彈性面域虛擬管道規(guī)劃及可行域?qū)Ρ确抡?/p>

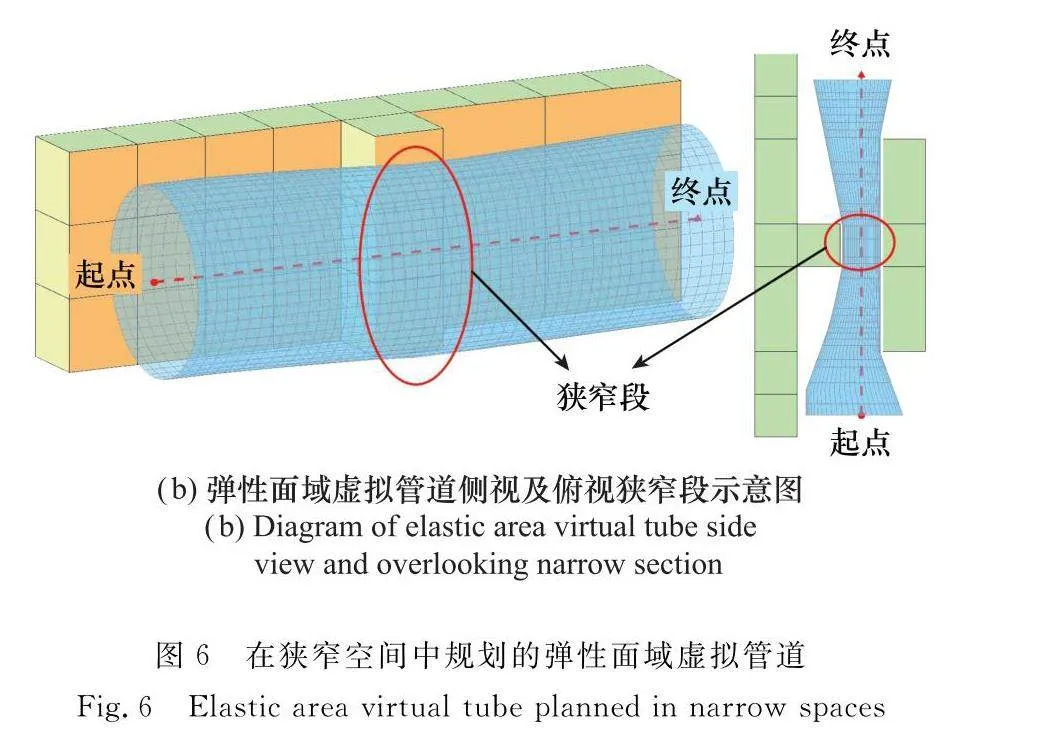
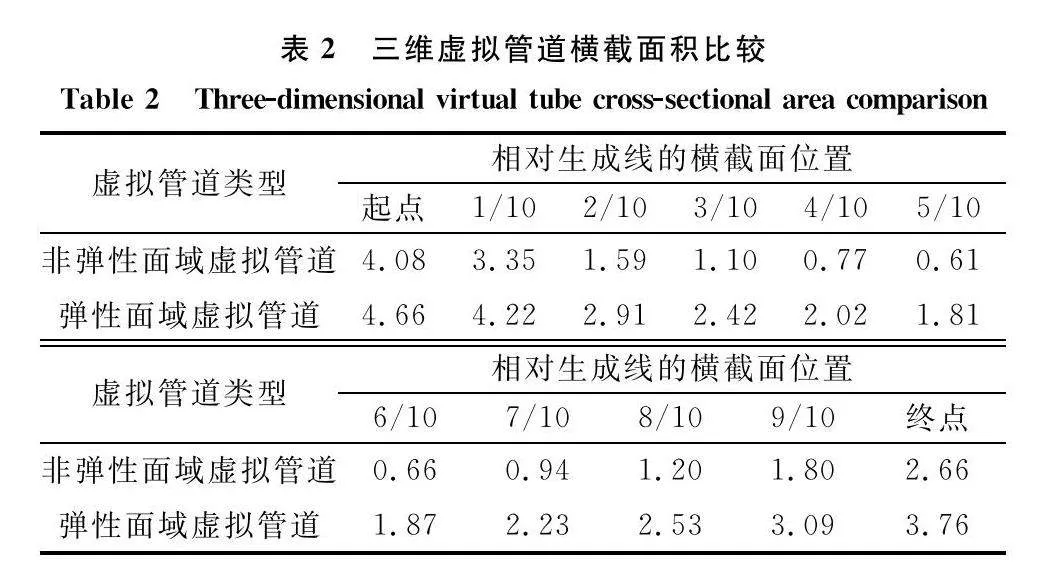
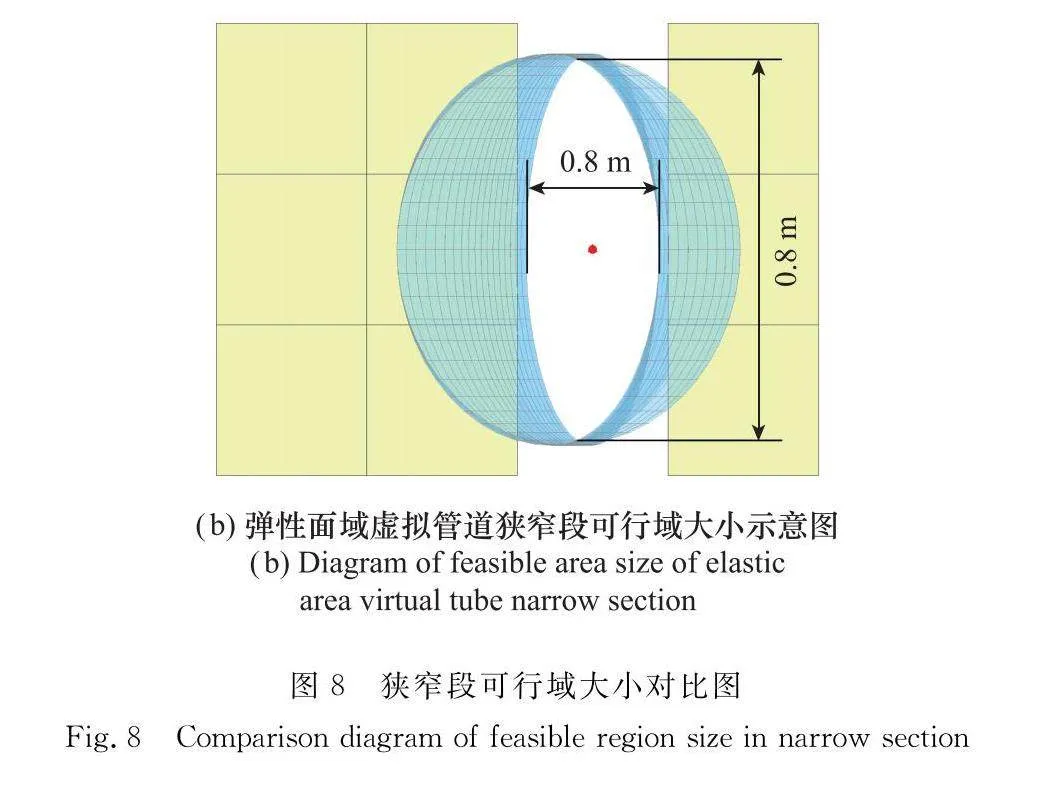
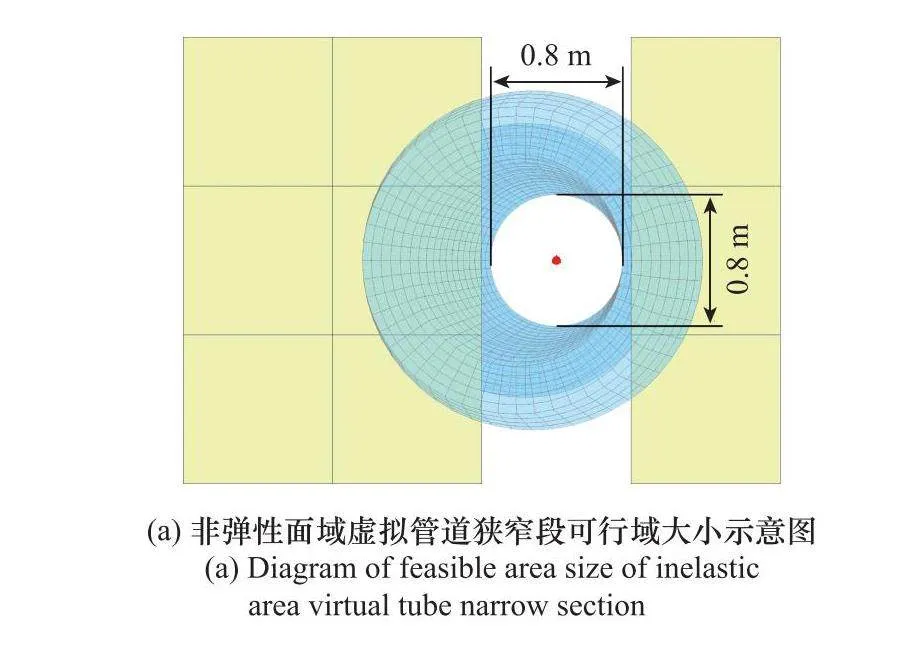
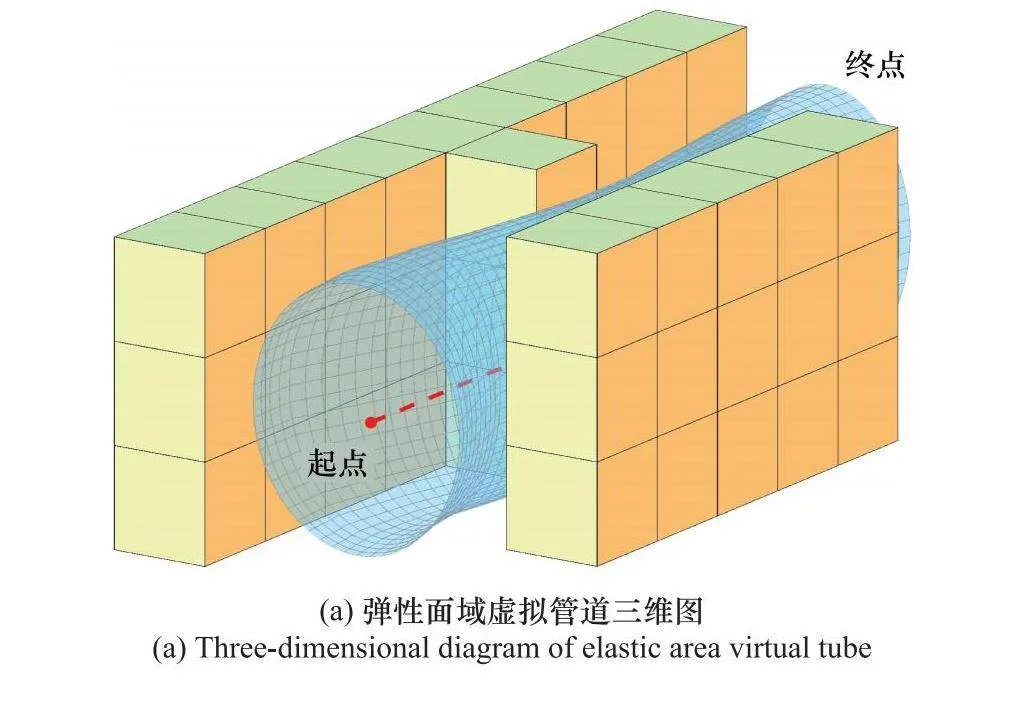
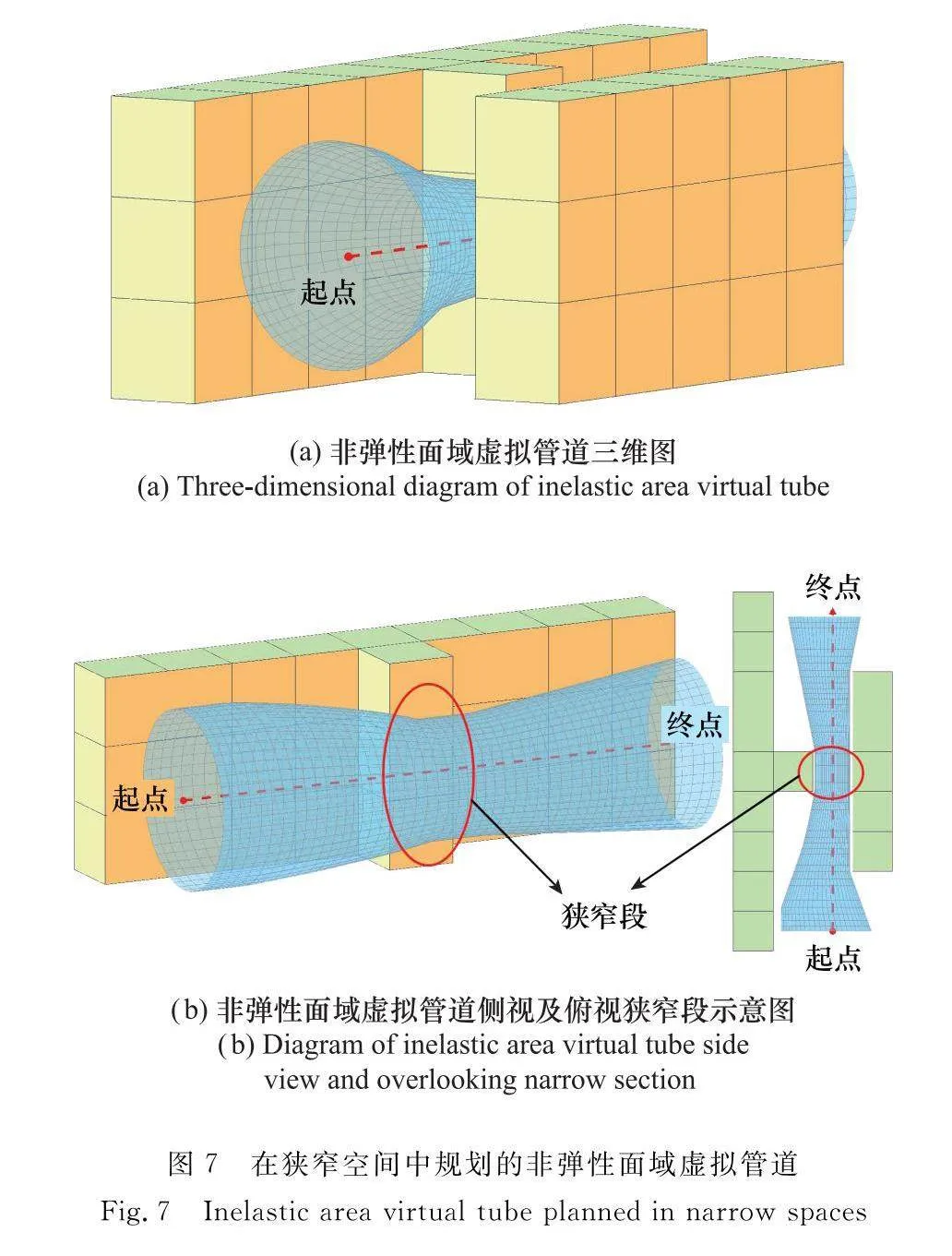
本節(jié)在10 m×10 m×3 m的柵格地圖中放置墻面障礙物，測試所提出的彈性面域虛擬管可行區(qū)域大小。在相同地圖中給定相同起點及終點的脊曲線;設(shè)置彈性面域虛擬管道主副半軸長最大值和非彈性面域虛擬管半徑最大值均設(shè)置為1.3 m，利用相同估價函數(shù)及各項參數(shù)，比較了改進前后的三維管道及脊曲線上11個不同位置的虛擬管道橫截面積大小，仿真結(jié)果如圖6～圖8和表2所示。

圖6與圖7對比了彈性面域虛擬管和非彈性面域虛擬管在柵格地圖中不同角度的管道形狀。從圖6與圖7中可以看出，在類似走廊、隧道中規(guī)劃管道時有一節(jié)狹窄段，該狹窄段使管道形成沙漏型，若狹窄段面積過小，會使通行的多智能體阻塞，延長通行時間。在同樣環(huán)境中對虛擬管道進行規(guī)劃，與非彈性面域虛擬管通行路徑始終保持圓截面不同，彈性面域虛擬管道兼容了更多可行空間，包含通道上下層領(lǐng)域，顯著增大了管道橫截面積，拓寬了多智能體可行范圍。

圖8對比了彈性面域虛擬管和非彈性面域虛擬管在柵格地圖中管道最小通行域大小。可以看到，非彈性面域虛擬管在狹窄段中最小通行域高度和寬度均只有0.8 m，而彈性面域虛擬管由于寬度受區(qū)域限制只有0.8 m以外，不受障礙物限制的高度可以達到規(guī)定最大限度，使彈性面域虛擬管道的橫截面積顯著大于非彈性面域虛擬管道。

從表2中的數(shù)據(jù)可以看出，彈性面域虛擬管在類走廊中規(guī)劃的橫截面積均大于非彈性面域虛擬管規(guī)劃的面積，這增強了多智能體在其中的流通性和效率，降低了阻塞風(fēng)險。

4.2 改進A*算法前后規(guī)劃對比仿真

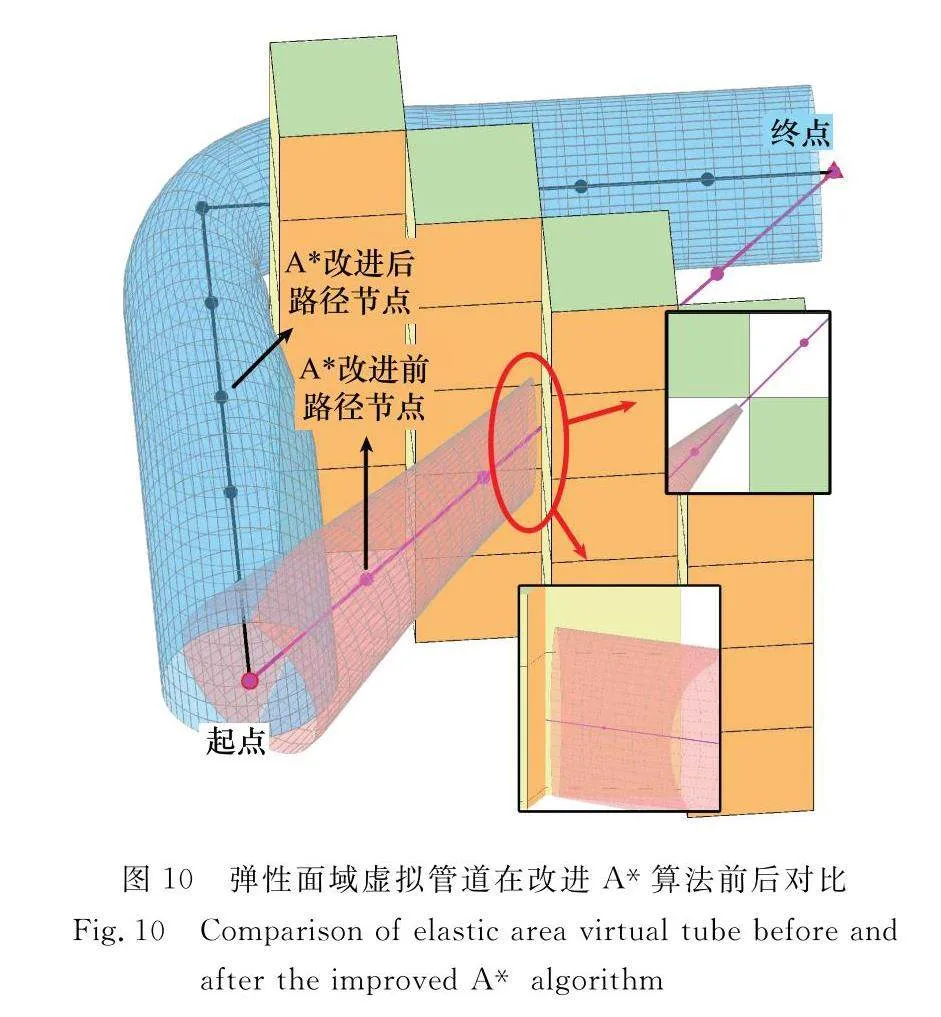
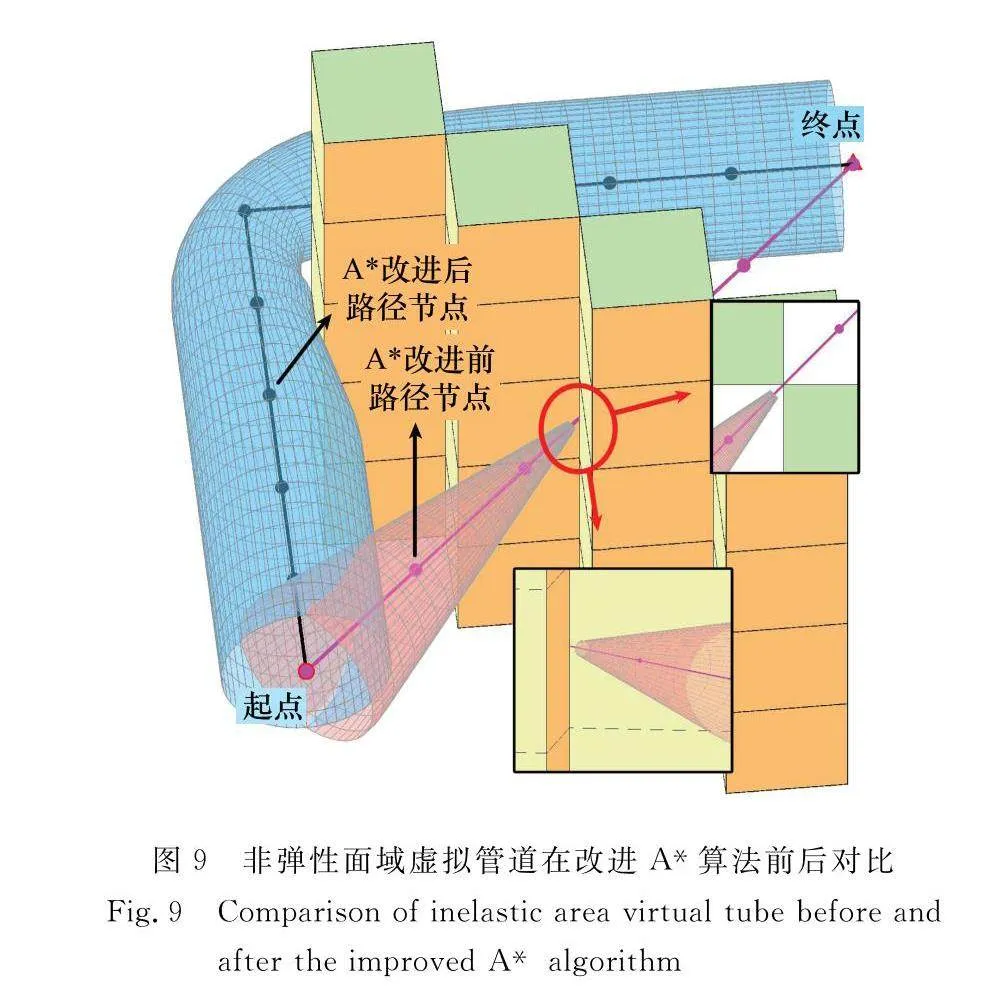
本節(jié)在6 m×6 m×5 m的相同三維柵格環(huán)境中對改進A*算法前后進行相同虛擬管道仿真比較。設(shè)置非彈性面域虛擬管道和彈性面域虛擬管道的最大管道半徑均為0.7 m，設(shè)置相同管道起點與終點，使用的管道估價函數(shù)及參數(shù)均一致，仿真結(jié)果如圖9和圖10所示。

從圖9和圖10中可以清晰地看到無論是否為彈性面域虛擬管道，在改進后的A*算法規(guī)劃下均能成功建立起點至終點的虛擬管道模型。在A*算法改進前，面對障礙物時算法會選擇對角線規(guī)劃，然而實際路線無法行進，且無空間建立管道模型;同時，在未改進算法規(guī)劃下的管道易出現(xiàn)規(guī)劃空間驟變，無法容納智能體通行的狀況。因此，在后續(xù)路徑中，管道模型均無法建立，從而致使管道無法規(guī)劃成功。

4.3 多智能體集群通行仿真

本節(jié)使用14個同性能多智能體在11 m×11 m×11 m的相同三維柵格環(huán)境中同時進行管道穿梭模擬。設(shè)置14個多智能體在起點端管道內(nèi)不同懸停位置以記錄初始時刻位置，進行了計時穿越，對比了多智能體在改進A*算法規(guī)劃下的非彈性面域虛擬管道和彈性面域虛擬管道內(nèi)集群穿梭的各項結(jié)果。

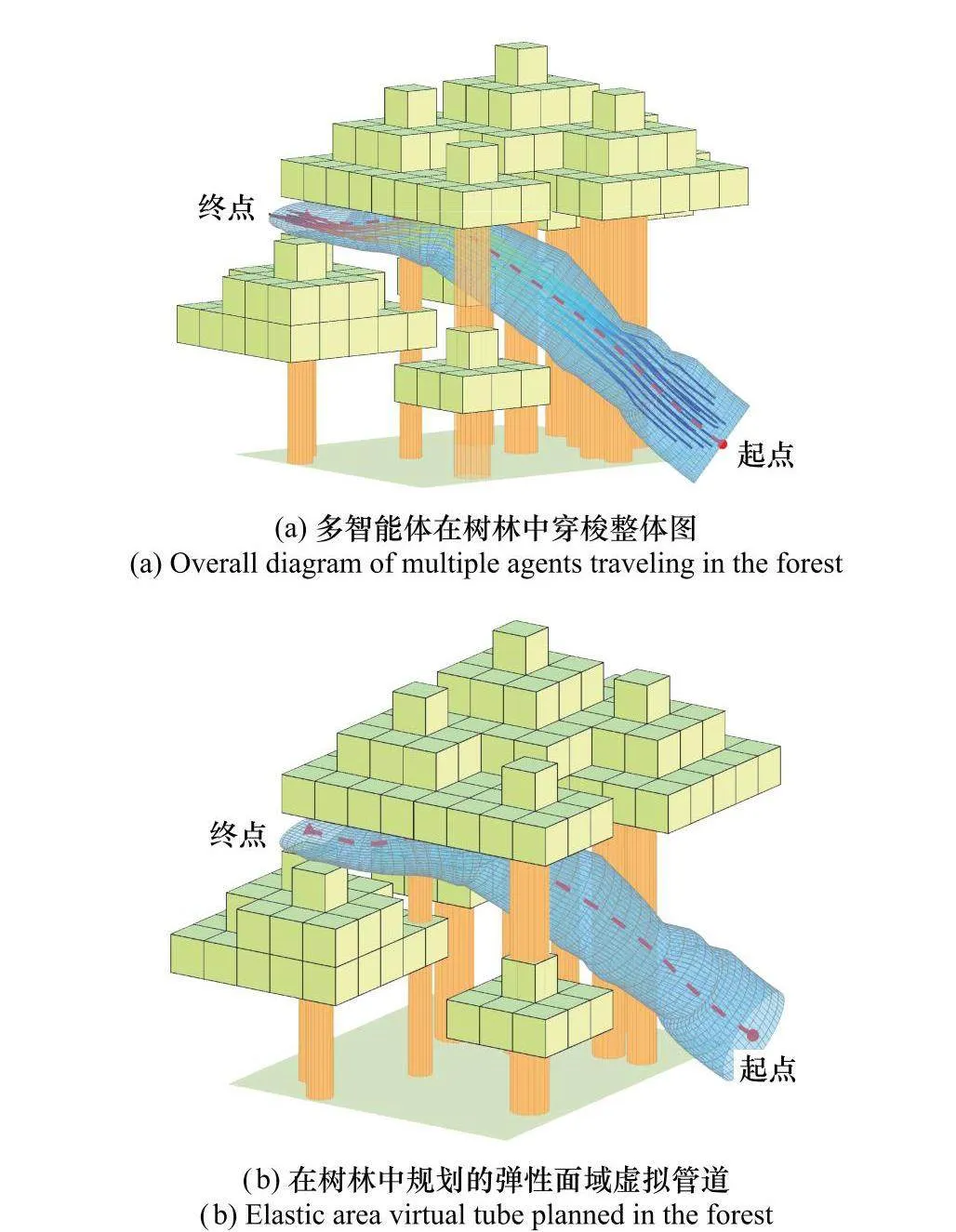
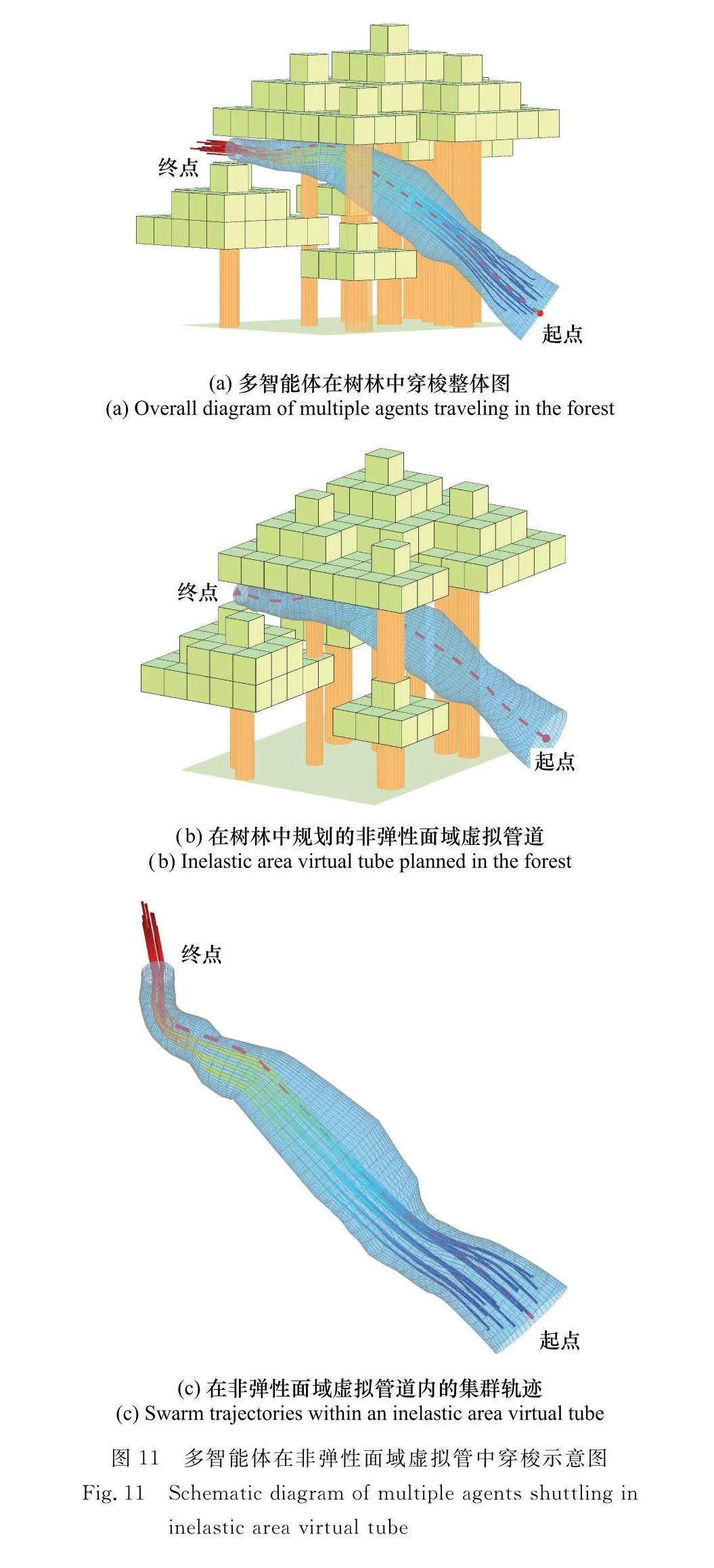
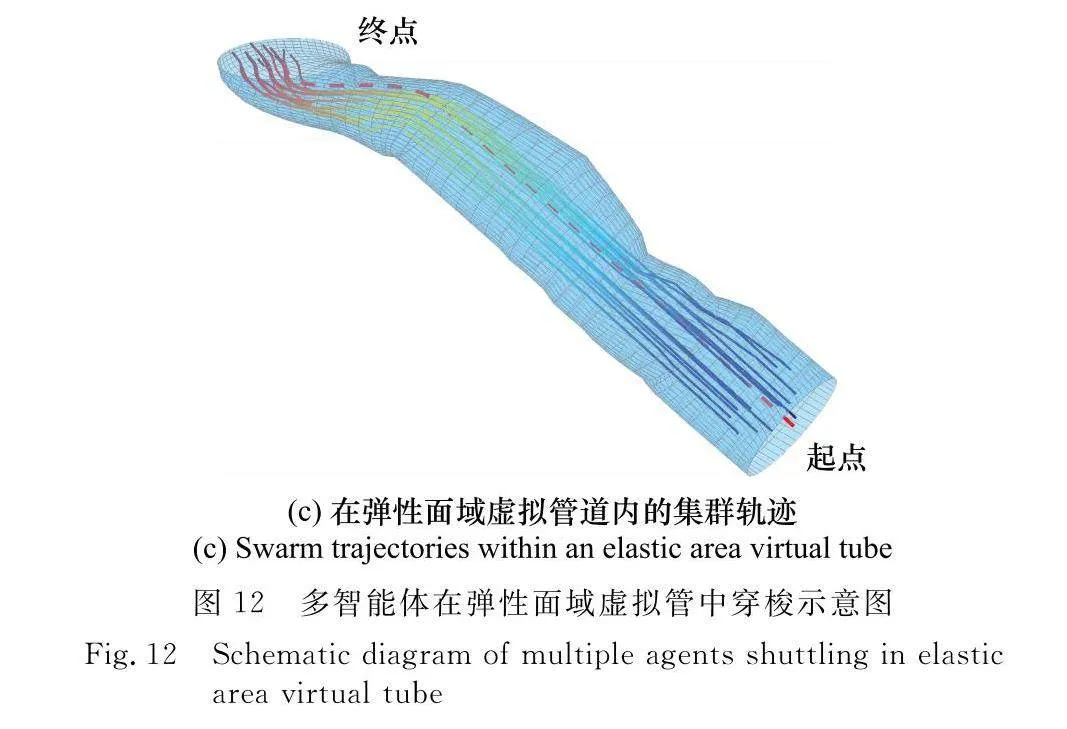
受文獻［24］的避障理論啟發(fā)，本文選取0.3 m作為避障距離，0.15 m為避碰距離。在大量隨機樹林生成中選出了比較直觀的環(huán)境圖，并在該環(huán)境中進行非彈性面域與彈性面域虛擬管道規(guī)劃。其次，使多智能體集群在這兩類管道內(nèi)模擬穿越，得到如圖11和圖12所示的仿真圖，圖中彩色方塊體及圓柱體是隨機生成的11棵樹;藍色透明面是生成的管道;紅色虛線是規(guī)劃的脊曲線;彩色實線是不同時刻多智能體的位置。

表3比較了多智能體在非彈性面域虛擬管道和彈性面域虛擬管道內(nèi)的穿越指標(biāo)，其中D_d表示多智能體之間最短距離;D_s表示多智能體與虛擬管道壁的最短距離;A_r表示多智能體成功穿越管道抵達管道另一端的抵達率。

從圖11（a）和圖12（a）中可以看到，多智能體集群在樹林環(huán)境下規(guī)劃出的虛擬管道內(nèi)穿梭;圖11（b）、圖12（b）和圖11（c）和圖12（c）分別顯示了虛擬管道在樹林環(huán)境中的規(guī)劃和多智能體在管道內(nèi)的穿越。可以看到，規(guī)劃管道遇到復(fù)雜密集障礙物時，彈性面域虛擬管道的可行空間遠比非彈性面域可行空間大，如圖11（c）和圖12（c），這樣可以使多智能體集群在穿越復(fù)雜環(huán)境時的可行域擴大，增強集群流通性。

從表3各項數(shù)據(jù)可以看到，在相同的避障策略、路徑規(guī)劃、控制策略、智能體參數(shù)下，彈性面域虛擬管道與非彈性面域虛擬管道內(nèi)多智能體集群穿越管道時相互之間的最小間距均為0.14 m，與管道壁的最小距離均為0.27 m，均未出現(xiàn)多智能體碰壁及碰撞墜毀現(xiàn)象。若運行總時間為7.35 s，在彈性面域虛擬管道內(nèi)的多智能體均成功穿越管道，而非彈性面域虛擬管道內(nèi)的多智能體只有92.8%完成穿越任務(wù);若運行7.56 s，非彈性面域虛擬管道中的多智能體才全部穿越管道。相比于非彈性面域虛擬管道，運行總時間為7.14 s時，彈性面域虛擬管道內(nèi)抵達管道終點的智能體數(shù)量已超過非彈性面域虛擬管道智能體數(shù)量的50%。

從上述的各項仿真可得，本文改進后的彈性面域虛擬管道有效增大了多智能體在虛擬管道中的流通量，減少了多智能體穿越管道的時間，提高了智能集群系統(tǒng)的性能，提升了多智能體系統(tǒng)在管道內(nèi)的魯棒性。

5 結(jié)束語

本文對正則虛擬管道進行可行面域的改進，提出彈性面域虛擬管道的概念，并對其定義進行完善。首先，該彈性面域管道在原有的正則虛擬管道基礎(chǔ)上增加一個可變半徑，以雙半徑共同規(guī)劃虛擬管道，進一步將三維空間中未被考慮到的空間利用規(guī)劃成為可行域。在走廊環(huán)境中進行仿真，對比非彈性面域虛擬管道和彈性面域虛擬管道的可行域大小，結(jié)果證明彈性面域虛擬管道的可行域范圍顯著大于非彈性面域虛擬管道可行域范圍。其次，在復(fù)雜樹林環(huán)境中進行14架多智能體穿越仿真，得到的結(jié)果均驗證了彈性面域虛擬管道能夠有效擴大多智能體在虛擬管道中流通量，減少集群穿越管道的總時間，提高智能集群系統(tǒng)的性能。在隨后的研究中，將會繼續(xù)深入研究多管道交叉的問題，以便進一步提高智能體在管道內(nèi)通行的效率。

參考文獻

［1］胡鵬林， 潘泉， 郭亞寧， 等. 多智能體編隊控制中的遷移強化學(xué)習(xí)算法研究［J］. 西北工業(yè)大學(xué)學(xué)報， 2023， 41（2）： 389-399.

HU P L， PAN Q， GUO Y N， et al. Study on learning algorithm of transfer reinforcement for multi-agent formation control［J］. Journal of Northwestern Polytechnical University， 2023， 41（2）： 389-399.

［2］張超省， 王健， 張林， 等. 面向復(fù)雜障礙場的多智能體系統(tǒng)集群避障模型［J］. 兵工學(xué)報， 2021， 42（1）： 141-150.

ZHANG C S， WANG J， ZHANG L， et al. A multi-agent system flocking model with obstacle avoidance in complex obstacle field［J］. Acta Armamentarii， 2021， 42（1）： 141-150.

［3］MADRIDANO A， AL-KAFF A， MARTíN D， et al. Trajectory planning for multi-robot systems： methods and applications［J］. Expert Systems with Applications， 2021， 173： 114660.

［4］YANG Y H， XIONG X Z， YAN Y H. UAV formation trajec-toryplanning algorithms： a review［J］. Drones， 2023， 7（1）： 62.

［5］GUO S， LIU B， ZhANG S， et al. Continuous-time Gaussian process trajectory generation for multi-robot formation via probabilistic inference［C］∥Proc.of the IEEE/RSJ International Conference on Intelligent Robots and Systems， 2021： 9247-9253.

［6］JING S C， ZHAO X M， HUI F， et al. Cooperative CAVs optimal trajectory planning for collision avoidance and merging in the weaving section［J］. Transportmetrica B： Transport Dynamics， 2021， 9（1）： 219-236.

［7］JACKSON B E， HOWELL T A， SHAH K， et al. Scalable cooperative transport of cable-suspended loads with UAVs using distributed trajectory optimization［J］. IEEE Robotics and Automation Letters， 2020， 5（2）： 3368-3374.

［8］QUAN Q， FU R， LI M X， et al. Practical distributed control for VTOL UAVs to pass a virtual tube［J］. IEEE Trans.on Intelligent Vehicles， 2021， 7（2）： 342-353.

［9］PARK J， KIM J， JANG I， et al. Efficient multi-agent trajectory planning with feasibility guarantee using relative bernstein polynomial［C］∥Proc.of the IEEE International Conference on Robotics and Automation， 2020： 434-440.

［10］SHI G Y， H?NIG W， SHI X C， et al. Neural-swarm2： planning and control of heterogeneous multirotor swarms using learned interactions［J］. IEEE Trans.on Robotics， 2021， 38（2）： 1063-1079.

［11］郭宏達， 婁靜濤， 楊珍珍， 等. 基于拍賣多智能體深度確定性策略梯度的多無人車分散策略研究［J］. 電子與信息學(xué)報， 2024， 46（1）： 287-298.

GUO H D， LOU J T， YANG Z Z， et al. Research on dispersion strategy for multiple unmanned ground vehicles based on auction multi-agent deep deterministic policy gradient［J］. Journal of Electronics amp; Information Technology， 2024， 46（1）： 287-298.

［12］DONG Z L， LIU C H. Collaborative coverage path planning of UAV cluster based on deep reinforcement learning［C］∥Proc.of the IEEE 3rd International Conference on Frontiers Technology of Information and Computer， 2021： 201-207.

［13］LI J， CAO S， LIU X J， et al. Trans-UTPA： PSO and MADDPG based multi-UAVs trajectory planning algorithm for emergency communication［J］. Frontiers in Neurorobotics， 2023， 16： 1076338.

［14］劉衛(wèi)國， 項志宇， 劉偉平， 等. 基于分布式強化學(xué)習(xí)的車輛控制算法研究［J］. 汽車工程， 2023， 45（9）： 1637-1645.

LIU W G， XIANG Z Y， LIU W P， et al. Research on vehicle control algorithm based on distributed reinforcement learning［J］. Aulomotive Engineering， 2023， 45（9）： 1637-1645.

［15］DORIGO M， THERAULAZ G， TRIANNI V. Swarm robotics： past， present， and future［point of view］［J］. Proceedings of the IEEE， 2021， 109（7）： 1152-1165.

［16］GUL F， MIR A， MIR I， et al. A centralized strategy for multi-agent exploration［J］. IEEE Access， 2022， 10： 126871-126884.

［17］ZHENG D， ZHANG Y F， LI F， et al. UAVs cooperative task assignment and trajectory optimization with safety and time constraints［J］. Defence Technology， 2023， 20： 149-161.

［18］LIN S W， LIU A， WANG J G， et al. A review of path-planning approaches for multiple mobile robots［J］. Machines， 2022， 10（9）： 773.

［19］QUAN L， YIN L J， ZHANG T R， et al. Robust and efficient trajectory planning for formation flight in dense environments［J］. IEEE Trans.on Robotics， 2023， 39（6）： 4785-4804.

［20］尹洋， 楊全順， 王征， 等. 通信距離約束下的無人船集群覆蓋搜索方法［J］. 系統(tǒng)工程與電子技術(shù)， 2022， 44（12）： 3821-3828.

YIN Y， YANG Q S， WANG Z， et al. USV cluster coverage search method with communication distance constraint［J］. Systems Engineering and Electronics， 2022， 44（12）： 3821-3828.

［21］LIU S， WATTERSON M， MOHTA K， et al. Planning dynamically feasible trajectories for quadrotors using safe flight corridors in 3-D complex environments［J］. IEEE Robotics and Automation Letters， 2017， 2（3）： 1688-1695.

［22］MAO P D， QUAN Q. Making robotics swarm flow more smoothly： a regular virtual tube model［C］∥Proc.of the IEEE/RSJ International Conference on Intelligent Robots and Systems， 2022： 4498-4504.

［23］GAO Y， BAI C G， QUAN Q. Distributed control for a multi-agent system to pass through a connected quadrangle virtual tube［J］. IEEE Trans.on Control of Network Systems， 2022， 2（10）： 693-705.

［24］QUAN Q， GAO Y， BAI C G. Distributed control for a robotic swarm to pass through a curve virtual tube［J］. Robotics and Autonomous Systems， 2023， 162： 104368.

［25］LIU L S， WANG B， XU H. Research on path-planning algorithm integrating optimization a-star algorithm and artificial potential field method［J］. Electronics， 2022， 11（22）： 3660.

［26］O’NEILL B. Elementary differential geometry［M］. 2nd ed. London： Elsevier， 2006.

［27］BILICI M， KOSEOGLU G. Tubular involutive surfaces with frenet frame in euclidean 3-space［J］. Maejo International Journal of Science and Technology， 2023， 17（2）： 96-106.

［28］MAEKAWA T. An overview of offset curves and surfaces［J］. Computer-Aided Design， 1999， 31（3）： 165-173.

［29］ELBER G， COHEN E. Error bounded variable distance offset operator for free form curves and surfaces［J］. International Journal of Computational Geometry amp; Applications， 1991， 1（1）： 67-78.

［30］SEONG J K， ELBER G， KIM M S. Trimming local and global self-intersections in offset curves/surfaces using distance maps［J］. Computer-Aided Design， 2006， 38（3）： 183-193.

［31］LEE I K， KIM M S， ELBER G. Planar curve offset based on circle approximation［J］. Computer-Aided Design， 1996， 28（8）： 617-630.

［32］MAEKAWA T， PATRIKALAKIS N M， SAKKALIS T， et al. Analysis and applications of pipe surfaces［J］. Computer Aided Geometric Design， 1998， 15（5）： 437-458.

［33］GAO F， WU W， LIN Y， et al. Online safe trajectory generation for quadrotors using fast marching method and bernstein basis polynomial［C］∥Proc.of the IEEE International Conference on Robotics and Automation， 2018： 344-351.

［34］LI Q， WEI J Y， GOU Q X， et al. Distributed adaptive fixed-time formation control for second-order multi-agent systems with collision avoidance［J］. Information Sciences， 2021， 564： 27-44.

作者簡介

吳尹菲（2000—），女，碩士研究生，主要研究方向為集群智能體路徑規(guī)劃。

李新凱（1991—），男，副教授，博士，主要研究方向為集群無人機路徑規(guī)劃與控制。

張宏立（1972—），男，教授，博士，主要研究方向為非線性系統(tǒng)動力學(xué)、工業(yè)系統(tǒng)故障診斷、無人系統(tǒng)控制、機器學(xué)習(xí)、群智能優(yōu)化。

陳穎穎（2000—），女，碩士研究生，主要研究方向為多智能體任務(wù)分配。

龔豐金（1996—），男，碩士研究生，主要研究方向為遷移學(xué)習(xí)、數(shù)字孿生、故障診斷。