回差矩陣奇異值方法改進和MIMO系統穩定性分析

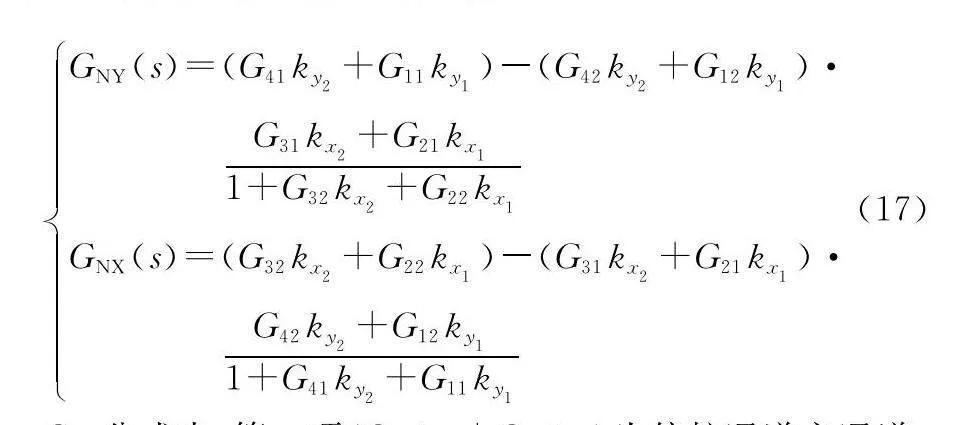
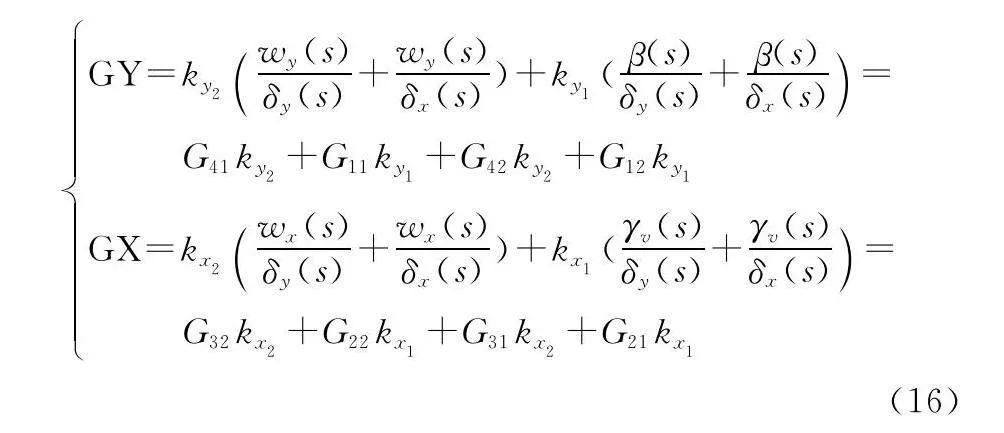
摘要： 高速防空導彈大攻角飛行時，耦合現象嚴重，彈體的高動態響應特征進一步加劇通道耦合，因此研究通道耦合下的系統穩定性至關重要。本文提出一種雙通道控制模式下，單通道斷開、耦合通道視為內回路的傳遞函數矩陣，并引入回差陣奇異值法計算系統穩定裕度。通過仿真將傳統奇異值法和基于傳遞函數矩陣的奇異值改進法計算出的穩定裕度、單通道穩定裕度、雙通道斷開的穩定裕度和基于通道耦合下的穩定裕度，結合系統的時域響應進行對比分析。結果表明，改進回差陣奇異值法計算結果更精確，通道耦合下的開環傳遞函數對系統穩定性描述更合理。

關鍵詞： 防空導彈; 穩定裕度; 回差陣最小奇異值; 開環傳遞函數

中圖分類號： V 448.2

文獻標志碼： A

DOI：10.12305/j.issn.1001-506X.2024.11.29

Improvement of return difference matrix singular value method and stability analysis of MIMO system

YAN Shuaihao^1，*， QIAN Rui¹， WEI Mingying^1，2， ZHENG Yongbin¹

（1. Beijing Institute of Electronic System Engineering， Beijing 100854， China;

2. Beijing Simulation Center， Beijing 100854， China）

Abstract： The coupling phenomenon is serious when the high speed air defense missile flies at high angle of attack， and the high dynamic response characteristics of the missile body further aggravate the channel coupling， so it is very important to study the system stability under the channel coupling. In this paper， a transfer function matrix is proposed in the two-channel control mode， in which the single channel disconnected and coupled channels are regarded as internal loop， and the return difference matrix singular value method is introduced to calculate the stability margin. The stability margin calculated by the traditional singular value method and the improved singular value method based on the transfer function matrix， the stability margin of single channel， the stability margin of double channel disconnection and the stability margin based on channel coupling are compared and analyzed by combining the time-domain response of the system. The results show that the improved residual matrix singular value method can obtain more accurate results， and the open-loop transfer function under channel coupling is more reasonable to describe the stability of the system.

Keywords： anti-aircraft missile; stability margin; minimum singular value of return difference matrix; open-loop transfer function

0 引 言

防空導彈的目標多為高速高機動的空中目標，因此對防空導彈的控制性能要求越來越高。在高速機動飛行時，橫側向通道存在嚴重的運動耦合，而且大攻角機動^［1］會進一步加劇耦合現象，此外還有氣動耦合、執行機構耦合和通道耦合（尤其是偏航和滾轉耦合）等，彈體模型中包含的耦合項種類較多，又由于目標的高速高機動特性，防空導彈自身需要高動態響應特征，這進一步加劇了耦合特性。而在工程設計時，穩定裕度代表了一個系統的穩定程度，是系統的開環頻率指標，其與閉環系統的動態性能密切相關，因此研究耦合對系統穩定裕度的影響至關重要。軸對稱外形的防空導彈耦合特性較小，在設計時主要為單通道，而單輸入單輸出（single-input-single-output， SISO）系統有成熟完備的頻域分析方法，如奈奎斯特法、Nichols、Bode圖等方法對系統的頻域進行分析，并計算系統穩定裕度^［2-3］。升阻比高的防空導彈^［4］由于耦合較多而且不是小量，無法再用單通道的分析方法，其本質變為了多輸入多輸出（multi-input multi-output， MIMO）系統的控制問題。而目前對MIMO系統穩定裕度的分析仍沒有統一明確的定義，也不能將傳統SISO系統的裕度分析方法直接推廣到MIMO系統中^［5-6］。最初對MIMO系統的穩定裕度的定義多為基于SISO分析方法，確定系統有幾條主通道，然后將所分析的主通道斷開求出對應的開環傳遞函數，再根據SISO分析法獲取其穩定裕度。這種方法所得到的裕度是在其他通道參數不發生變化情況下，系統允許該通道發生的幅值或相角變化^［7］，文獻［8］將MIMO系統穩定裕度與拆分為SISO系統最小穩定裕度進行對比。目前，解決MIMO系統穩定裕度分析大致有以下幾種方法：Gershgorin圓盤法^［9］、基于結構奇異值的u分析方法^［10］、多回路穩定分析法、回差矩陣奇異值方法等。文獻［11］利用系統的特征根軌跡繪制系統的幅值和相位穩定邊界，文獻［12］研究平衡靈敏度函數、互補靈敏度函數、靈敏度函數的MIMO穩定裕度和保守性，其中回差陣奇異值法取得了較好的效果，通過系統回差矩陣最小奇異值的理論確定了MIMO系統的穩定裕度^［13-14］。文獻［15］先通過時域控制性能指標確定控制參數優化范圍，然后利用奇異值法評估MIMO系統得穩定裕度，從而確定最優的控制參數。同樣，文獻［16］也利用回差陣奇異值法設計滿足系統穩定裕度要求得參數范圍，并在此基礎上進行尋優。

文獻［7］以飛控系統為背景詳細介紹如何利用回差陣奇異值法計算MIMO系統的穩定裕度并改進了該方法的保守性。文獻［17］通過將回差矩陣奇異值和逆回差矩陣奇異值相結合計算系統穩定裕度降低回差陣的保守性，對多衛星控制系統進行頻域分析。文獻［18］同樣為改善回差陣奇異值法計算的保守性，采用結構奇異值分析不確定系統穩定裕度的u法。文獻［19］采用閉環系統回差陣奇異值分析方法評估MIMO控制系統的穩定裕度。

目前對回差陣奇異值方法求穩定裕度的研究以及對其計算保守性的改進的研究都較多，在使用回差陣奇異值方法時其開環傳遞函數都是用狀態空間描述的開環傳遞函數，而開環傳遞函數的表達形式也并不僅此一種，因此本文在應用回差陣奇異值方法中，開展不同的開環傳遞函數描述方法下系統穩定裕度研究。同時，通過仿真分析通道耦合對系統穩定裕度的影響。

1 橫側向耦合姿態動力學模型

由于防空導彈的復雜耦合特性，滾轉和偏航回路無法再使用單通道設計，轉而將兩通道聯合組成橫側向耦合姿態模型，得到簡化后的橫側向繞質心轉動的4階小擾動運動方程，如下所示：

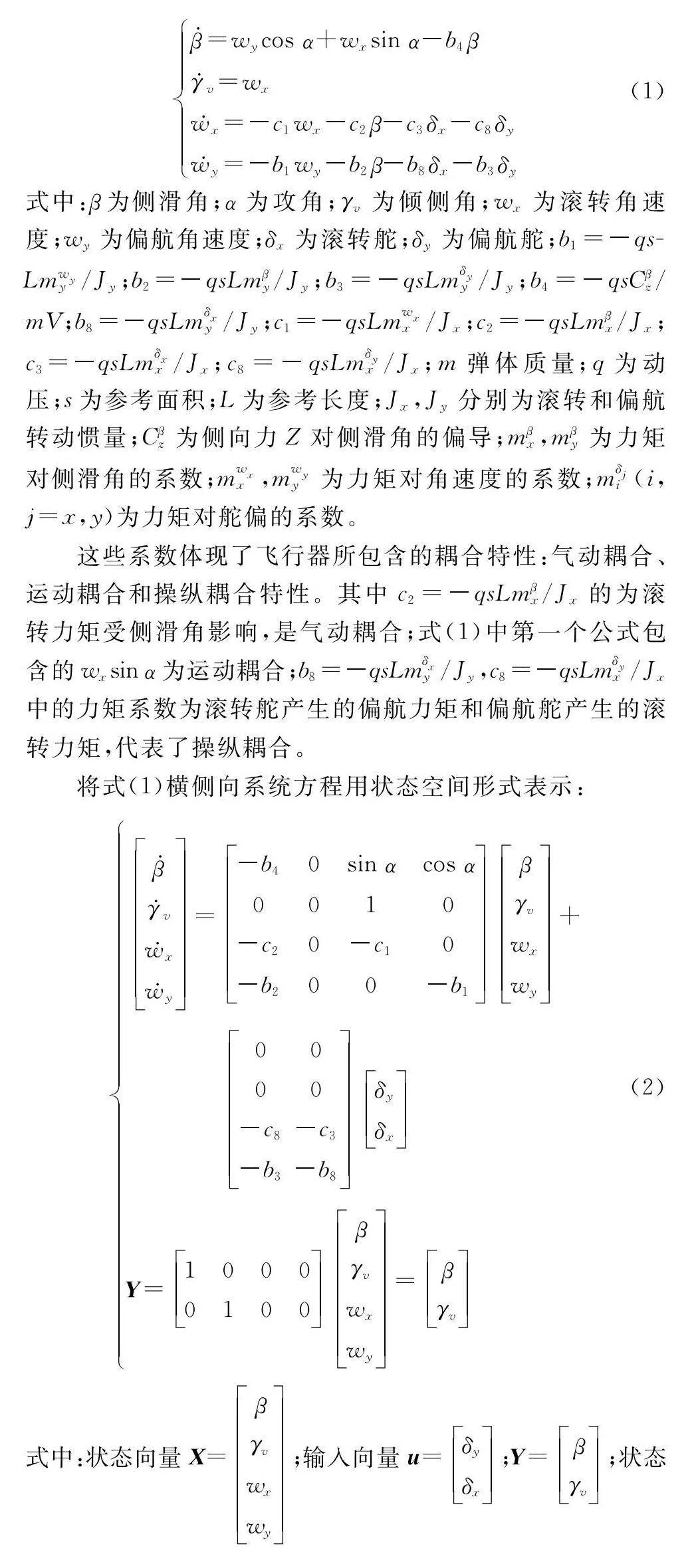
式中：β為側滑角;α為攻角;γ_v為傾側角;w_x為滾轉角速度;w_y為偏航角速度;δ_x為滾轉舵;δ_y為偏航舵;b₁=－qsLm^w_yy/J_y;b₂=－qsLm^β_y/J_y;b₃=－qsLm^δ_yy/J_y;b₄=－qsC^β_z/mV;b₈=－qsLm^δ_xy/J_y;c₁=－qsLm^w_xx/J_x;c₂=－qsLm^β_x/J_x;c₃=－qsLm^δ_xx/J_x;c₈=－qsLm^δ_yx/J_x;m彈體質量;q為動壓;s為參考面積;L為參考長度;J_x，J_y分別為滾轉和偏航轉動慣量;C^β_z為側向力Z對側滑角的偏導;m^β_x，m^β_y為力矩對側滑角的系數;m^w_xx，m^w_yy為力矩對角速度的系數;m^δ_ji（i，j=x，y）為力矩對舵偏的系數。

這些系數體現了飛行器所包含的耦合特性：氣動耦合、運動耦合和操縱耦合特性。其中c₂=－qsLm^β_x/J_x的為滾轉力矩受側滑角影響，是氣動耦合;式（1）中第一個公式包含的w_xsin α為運動耦合;b₈=－qsLm^δ_xy/J_y，c₈=－qsLm^δ_yx/J_x中的力矩系數為滾轉舵產生的偏航力矩和偏航舵產生的滾轉力矩，代表了操縱耦合。

將式（1）橫側向系統方程用狀態空間形式表示：

本文主要為研究耦合對穩定裕度的影響，為更清晰展示，選擇采用傳統的比例微分（proportion-derivative， PD）控制器。令期望姿態角為Y^*=［β^*，γ^*_v］，姿態角誤差為e=Y－Y^*，設計系統控制器為

式中：k_xi，k_yi（i=1，2）為系統待設計參數;β_c，γ_vc分別為側滑角指令和滾轉角指令。用K，b，v將式（3）中的參數矩陣和姿態角指令輸入表示為K=k_y100k_y2

γ_vc，代入控制器后系統可化為

控制結構如圖1所示。

2 回差陣奇異值法

系統的穩定裕度由幅值裕度和相位裕度構成，在原系統中加入一個對角陣（量測陣），該對角陣通過增加原系統的控制增益和延遲原系統相位使其達到臨界穩定，此時該矩陣的增益和相位就表示了原系統的幅值裕度和相位裕度。這就是回差陣奇異值法的思想。圖2為回差陣奇異值法計算MIMO系統的穩定裕度，G（s）為被控對象，K（s）為反饋控制器，L（s）=diag（l₁，l₂，…，l_n）為測量裕度的量測矩陣，其中l_i=k_ie^φ_i^j（i=1，2，…，n）是可變復數，k_i表示增益，φ_i表示相位。當系統正常工作時k_i=1，φ_i=0，L為單位矩陣。

2.1 回差陣定義

由經典控制穩定判據中可知，系統閉環傳遞函數為Φ（s）=G（s）/［I+G（s）K（s）］，則其特征多項式為I+G（s）·K（s），決定了系統的穩定性。

MIMO系統在某處斷開后，從輸入到輸出之間的誤差傳遞函數矩陣就是系統的回差陣^［20］。如圖2（a）所示，系統在a處斷開，a′處信號為I，從a′到a處傳遞函數為-G（s）K（s），兩處誤差傳遞函數陣為I+G（s）K（s），因此可知對于MIMO系統，閉環系統的穩定性取決于系統回差矩陣的零點位置，不僅希望全部零點在S平面的左半平面，而且希望到原點有一定“距離”，從而使系統受到一定擾動后依舊保持穩定。

2.2 奇異值求穩定裕度

由矩陣奇異值^［21］求解公式σ（A）=λ（A^HA）可知，矩陣的最大奇異值σ-（A）等于矩陣的二范數，表達式為σ-（A）=maxλ（A^HA）=A₂，二范數可以表征空間中兩點之間的直線距離。由奇異值與特征值的關系σ₁（A）≥|λ_i（A）|≥σ_n（A）（i=1，2，…，n）可知，最小奇異值小于等于回差陣的最小特征值，最小特征值代表了系統方程的根與原點之間的最小距離。因此，當回差矩陣中的最小奇異值大于零時，系統穩定。

若加入攝動矩陣后的閉環系統保持穩定，根據回差陣奇異值可知，系統的回差陣是非奇異的，滿足以下關系：

式中：σ-（·）表示矩陣的最小奇異值。將式（5）進一步推導，由于L（s）為對角陣因此為非奇異，推導得

又因為系統本身是穩定的，因此（I+KG）非奇異，因此系統可等價為

根據奇異值相關知識^［17］：

由式（7）與式（8）可知，若σ-［（L^－1－I）（I+KG）^－1］≤σ-（L^－1－I）σ-（I+KG）lt;1成立，則使（L^－1－I）（I+KG）^－1₂lt;1成立的充分條件為

式中：L（s）取為對角陣，由奇異值計算^［19］可將式（9）系統穩定的充分條件化為

由于原系統已知，因此式（10）右端在任何頻率下都可直接求出，σ-［I+KG］=m，當原系統確定后m也隨之確定，式（10）可轉化為

令式（11）中的k_i=1可計算系統相位裕度，φ_i=0可計算系統幅值裕度PM和相位裕度GM：

3 基于新傳遞函數矩陣的回差陣

3.1 單通道系統開環傳遞函數

MIMO系統在奇異值方法中需要獲取系統的開環傳遞函數。在求解開環傳遞函數時通常是將反饋矩陣斷開進而求得系統開環傳遞函數，然而在反饋矩陣斷開時，系統內部結構是如何斷開無法知曉。因此，嘗試以單通道開展兩種表達形式的驗證，研究傳統從舵系統環節前斷開和狀態空間描述下求取的開環傳遞函數的差異性。

單通道系統的控制結構圖^［22］，如圖3所示。

圖3中，k₁，k₂為系統控制參數，r_c為指令，r_b為狀態;工程中通常將系統在舵處（叉號處）斷開來獲得系統的開環傳遞函數：

由系統結構可知該單通道的模型為

用狀態空間表示為

由圖3系統的控制結構可得系統的輸入為狀態反饋δ=［k₂，k₁］［γ_v，w_x］^T+v，構成了狀態反饋系統，如圖4所示。

狀態空間在求系統開環傳遞函數時將系統從反饋處斷開求其開環傳遞函數：

由式（13）和式（14）可知，二者相同即可得出結論：狀態空間求出的開環傳遞函數與圖3中結構求出的系統開環傳遞函數相同。

3.2 雙通道傳遞函數矩陣

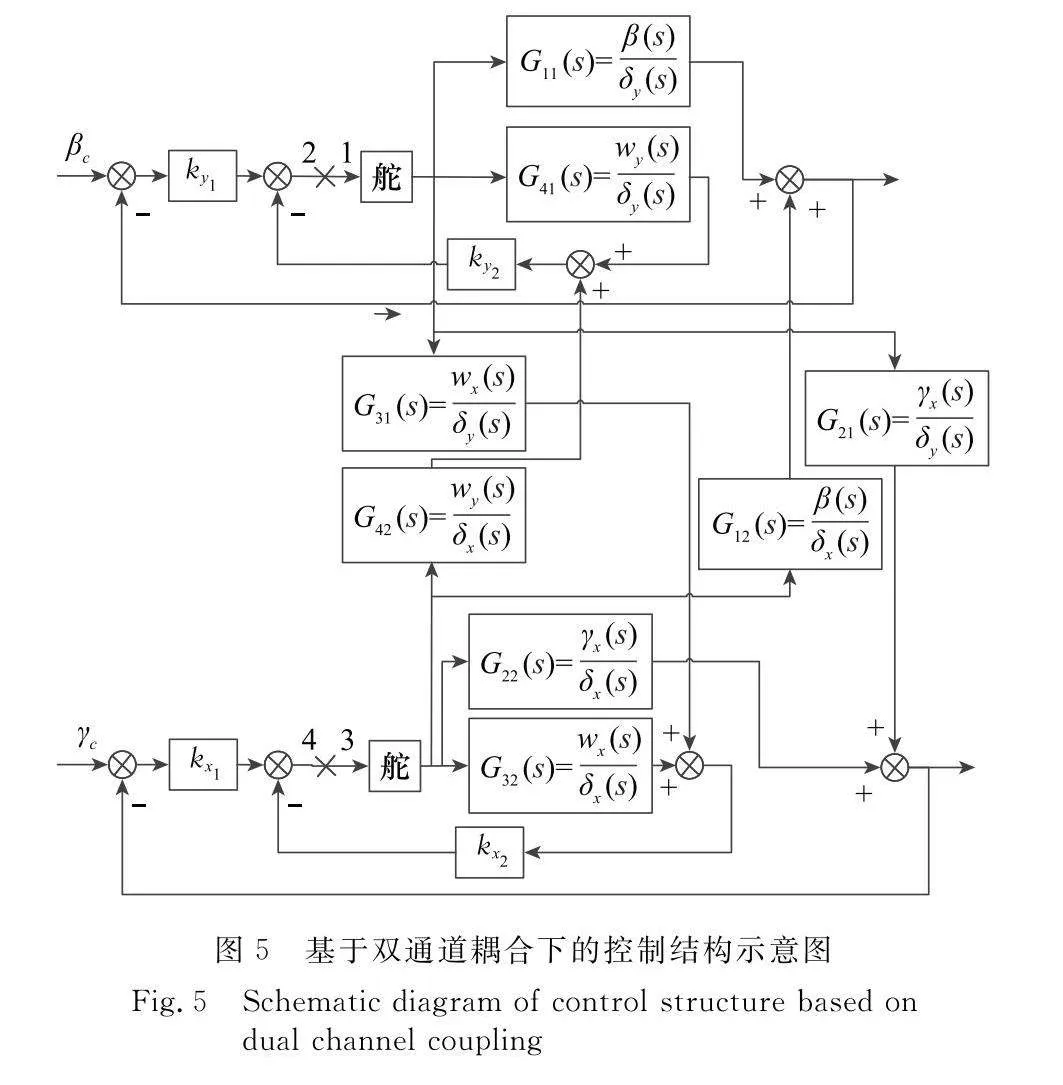
將第3.1節對單通道獲取開環傳遞函數的兩種方法向雙通道推廣，雙通道系統在獲取開環傳遞函數時，圖4中的反饋通道打開表示兩個通道在反饋處同時斷開。為進一步認識雙通道系統內部結構，將系統的狀態空間表達形式轉化為基于雙通道耦合下的控制結構示意圖。

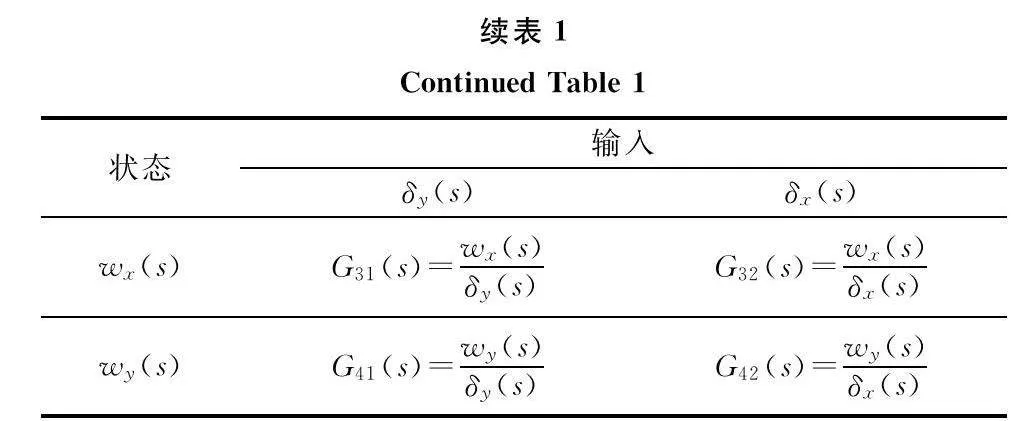
首先將式（1）系統的輸出矩陣C改為單位矩陣，系統將轉化為一個兩輸入四輸出系統，求其傳遞函數獲得每個狀態與輸入之間的函數關系，如表1所示。

由表1所獲得的每個狀態和輸入之間關系可將系統的狀態空間表達形式轉化為結構圖形式，如圖5所示。

由狀態空間求開環傳遞函數的結果可知系統為雙入雙出，因此雙通道結構圖需要斷開兩處，將單通道做一個推廣，在偏航通道中，與滾轉通道斷開處相同的位置也斷開。為得到了以位置1和3處為輸入，位置2和4處為輸出的雙通道系統，進而求1入2出、1入4出、3入2出和3入4出的傳遞函數如下所示：

組成傳遞函數矩陣G_tro可為

由此表明，系統狀態空間表述系統的開環傳遞函數，是將雙通道在相應位置都斷開進而聯合計算系統開環傳遞函數矩陣。

傳遞函數矩陣G_tro中，k_y1G11+k_y2G41表示偏航的主通道傳遞函數，k_y1G12+k_y2G42表示偏航通道的通道耦合項;k_x1G21+k_x2G31表示滾轉主通道傳遞函數，k_x1G22+k_x2G32表示滾轉通道的通道耦合項。則將圖5中位置1和3為輸入，位置2為輸出時的傳遞函數定義為偏航通道的傳遞函數GY;同理，位置1和3為輸入，位置4為輸出時的傳遞函數定義為滾轉通道的傳遞函數GX，如下所示：

由式（16）中兩通道的開環傳遞函數可直接利用傳統頻域分析法來計算每個通道的穩定裕度。

3.3 基于所提傳遞函數矩陣的奇異值改進方法

傳統在求解回差陣奇異值法求穩定裕度所用的系統開環傳遞函數時，是將雙通道在相同的位置斷開，求系統的開環傳遞函數矩陣。本文探討另外一種傳遞函數矩陣方法：斷開其中一條通道，將另外耦合通道視為其內回路獲取開環傳遞函數。

將圖5結構在位置1處斷開，將獲得偏航通道為主通道，滾轉通道為耦合回路的開環結構，由此可求其開環傳遞函數G_NY，同理可求出滾轉為主通道，偏航通道為耦合回路時的開環傳遞函數G_NX，可分別表示為

G_NY公式中，第一項（G₄₁k_y2+G₁₁k_y1）為偏航通道主通道，第二項（G₄₂k_y2+G₁₂k_y1）為偏航通道耦合項，（G₃₁k_x2+G₂₁k_x1）為滾轉通道的通道耦合項，（G₃₂k_x2+G₂₂k_x1）為滾轉主通道;第二項將偏航通道和滾轉通道的通道耦合以及滾轉主通道放在一起視為偏航通道的內回路。G_NX公式中，第一項（G₃₂k_x2+G₂₂k_x1）為滾轉通道主通道，第二項中（G₃₁k_x2+G₂₁k_x1）為滾轉通道耦合項，（G₄₂k_y2+G₁₂k_y1）為偏航通道的通道耦合項，（G₄₁k_y2+G₁₁k_y1）為偏航主通道;第二項將滾轉通道和偏航通道的通道耦合以及偏航主通道放在一起視為滾轉通道的內回路。

將所求出的G_NX和G_NY組成系統的開環傳遞函數矩陣G_N（s）=G_NY（s）0

0G_NX（s），新的傳遞函數矩陣為對角陣，而且其系統內部的所有耦合都包含在對角元素內，G_NY中不僅有偏航通道主回路的傳遞函數，還有滾轉通道的元素;G_NX中不僅有滾轉通道主回路的傳遞函數，還有偏航通道的元素，如下所示：

4 仿真分析

仿真分析主要分為兩部分：MIMO頻域分析和經典頻域分析。MIMO頻域分析是將傳統回差矩陣奇異值法和改進后回差矩陣奇異值法計算的穩定裕度進行對比分析，表明改進后回差矩陣奇異值法計算的穩定裕度更精確。經典頻域分析是將忽略耦合的單通道穩定裕度、斷開兩處（見式（16）中的GY，GX）的穩定裕度和斷開一處（見式（17）中的G_NY，G_NX）的穩定裕度進行分析，將單通道穩定裕度與式（17）計算的穩定裕度進行對比分析可得到耦合對系統穩定裕度的影響。式（16）對應斷開兩處的傳統回差矩陣奇異值法中的傳遞函數矩陣，式（17）對應一處斷開的改進回差矩陣奇異值法中的傳遞函數矩陣。將式（16）計算的穩定裕度與式（17）計算的穩定裕度進行對比分析可進一步驗證改進回差矩陣奇異值法計算的穩定裕度更精確。

4.1 回差陣

本文中的遠程防空導彈的橫側向系統小擾動線性化后是兩輸入兩輸出線性模型，為驗證所提出新的回差陣奇異值計算系統穩定裕度方法的優越性以及分析耦合對系統穩定裕度的影響，以飛行中某處的特征點為基準狀態，根據所設計的控制器進行穩定裕度的評估和對比。飛行器的滾轉通道使滾轉角從0°變化至30°，偏航通道使側滑角保持在0°，舵偏小于25°。

特征點處狀態為：飛行高度20 km，飛行速度6馬赫，攻角為30°，初始側滑角為2°。

系統控制器參數取為

K=0.45001.799

00.074 70.3740（19）

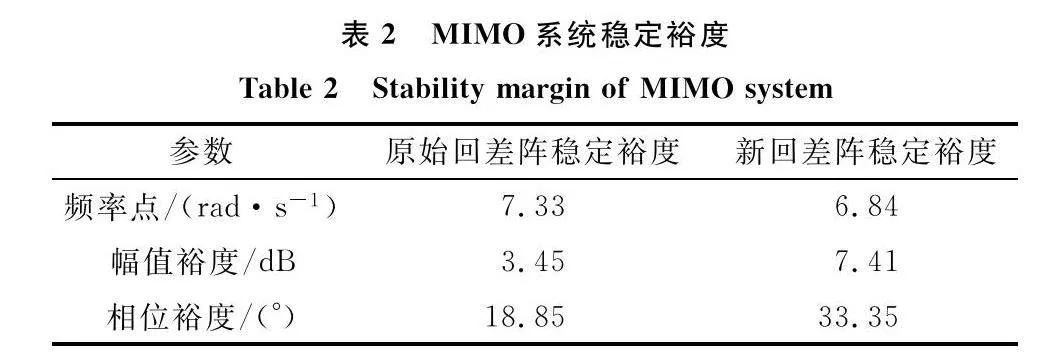
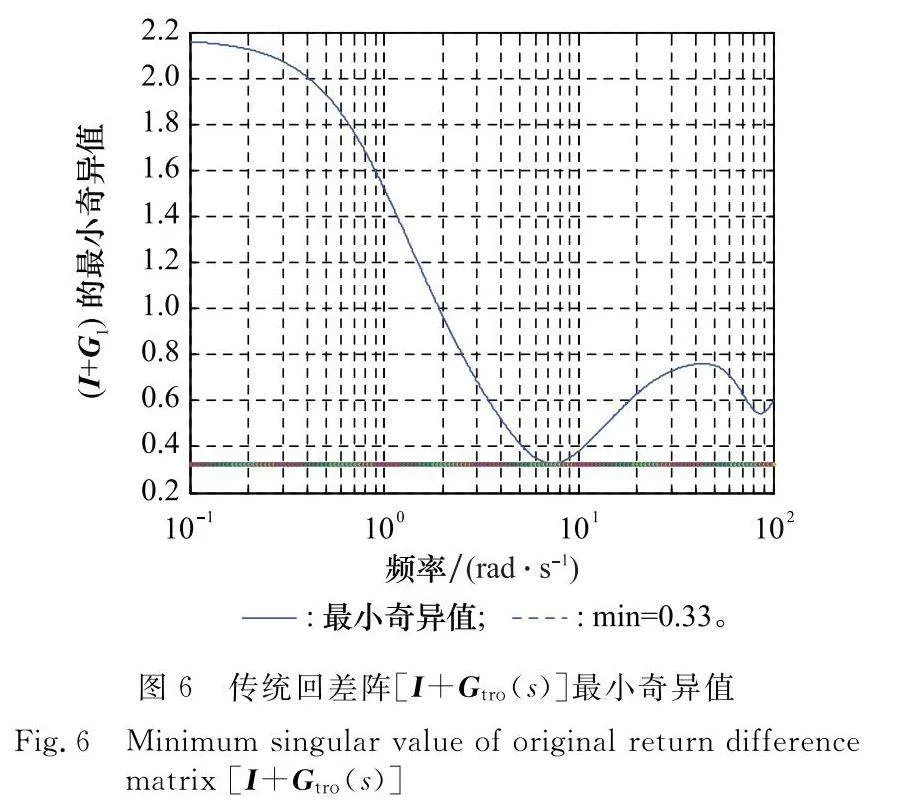
在原系統中加入攝動矩陣（量測矩陣）L（s）=diag（k₁e^φ₁^j，k₂e^φ₂^j，…，k_ne^φ_n^j），根據傳統的回差矩陣奇異值評估方法計算系統的穩定裕度，可得回差陣［I+G_tro（s）］的最小奇異值如圖6所示，得σ-［I+G_tro（s）］=0.33，由式（12）可得各通道幅值固定時，系統的相位裕度是18.85°;各通道相位固定時，系統的幅值裕度是3.45 dB。

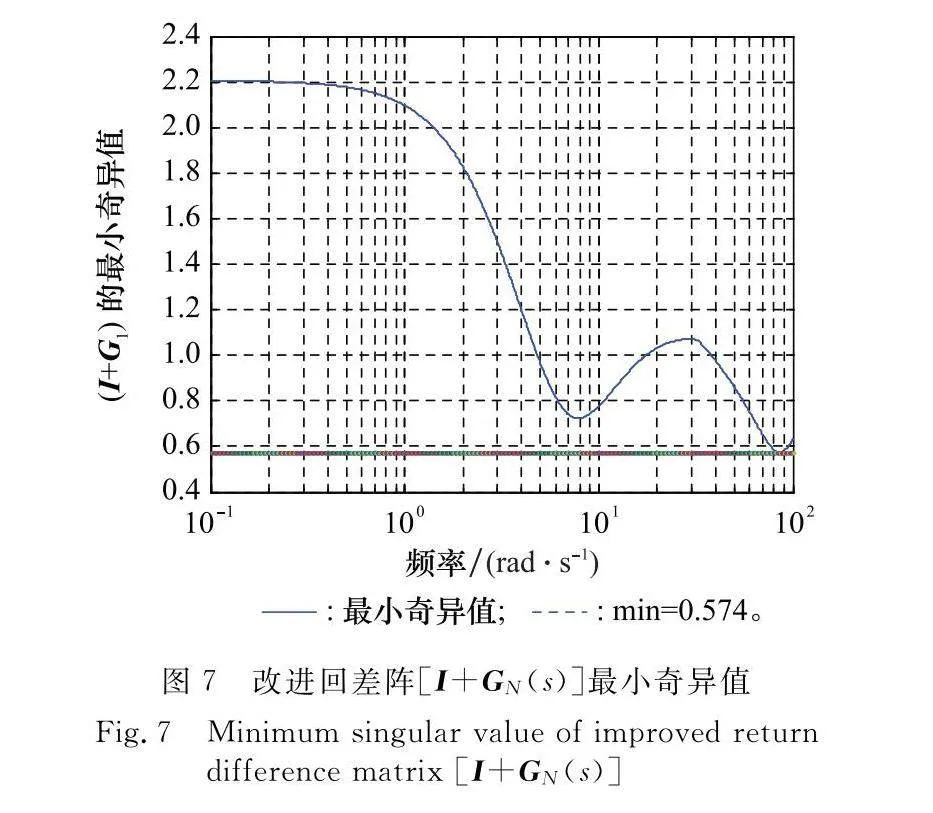
將傳統回差陣奇異值法中的傳遞函數矩陣G_tro（s）換為轉換后的對角陣G_N（s），在系統新傳遞函數矩陣G_N（s）處加入攝動陣L（s）=diag（k₁e^φ₁^j，k₂e^φ₂^j，…，k_ne^φ_n^j），回差陣［I+G_N（s）］的最小奇異值如圖7所示，得σ-［I+G_N（s）］=0.574，由式（12）可得當所有通道的幅值不變時，允許所有通道的相位裕度是33.35°;當所有通道相位不變時，允許所有通道的幅值裕度是7.41 dB。

由圖6和圖7可看到，對比二者用回差陣奇異值所求出的結果可以看到，改善后的回差陣所得到的裕度要大于傳統的回差陣。

4.2 通道耦合對穩定裕度的影響

將基于式（17）中耦合下的系統穩定裕度與忽略耦合時的單通道系統的穩定裕度進行對比，得到通道耦合下對主通道穩定裕度的影響。

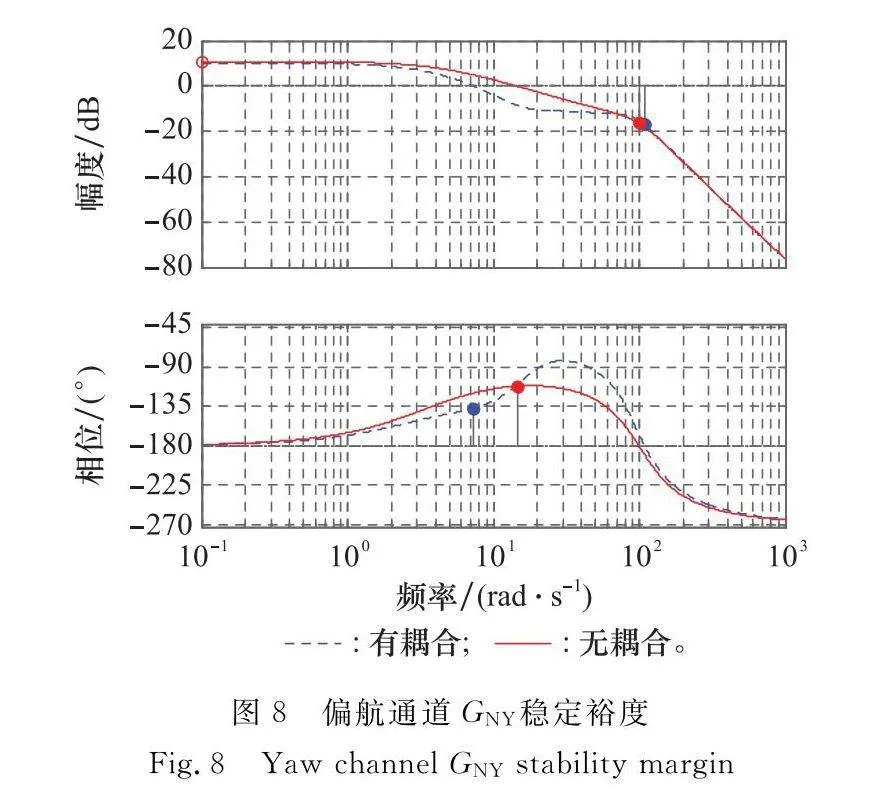
由圖5結構（在位置1和3處分別斷開得到的基于通道耦合下的傳遞函數G_NY，G_NX）可以求取偏航和滾轉通道在有無耦合情況下的穩定裕度，以此研究耦合對系統穩定裕度的影響。

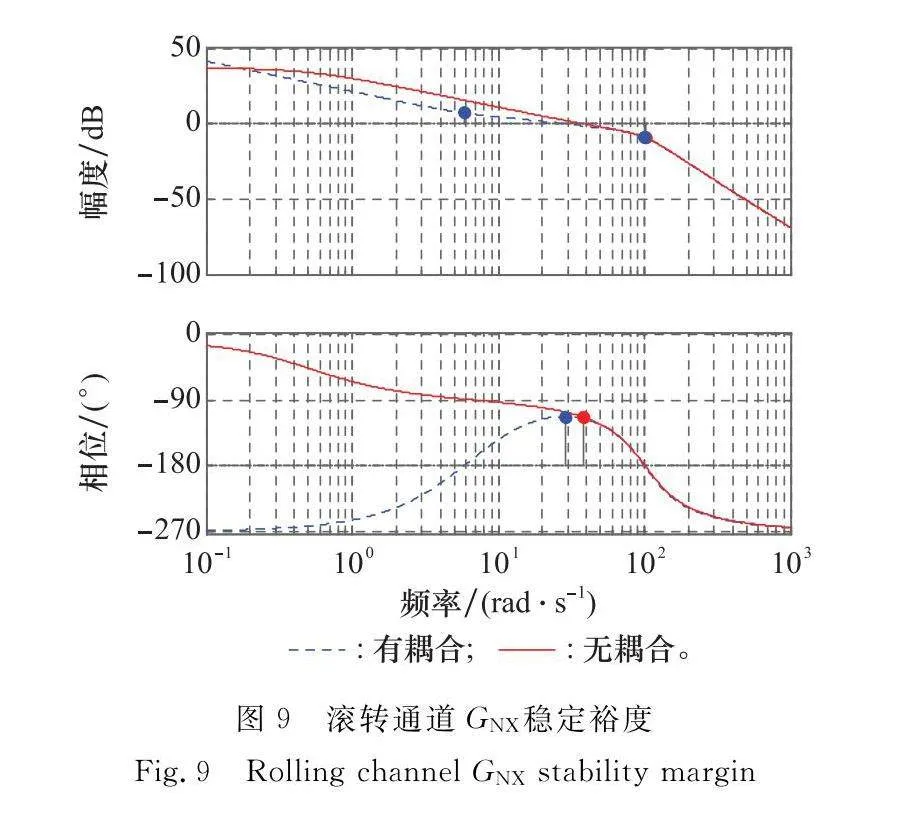
偏航通道G_NY穩定裕度如圖8所示。滾轉通道G_NX穩定裕度如圖9所示。

由圖8和圖9可知，基于耦合下的系統穩定裕度小于單通道時的穩定裕度，即耦合降低了系統的穩定裕度。

由第3.2節，將圖5結構在位置1、3處同時斷開得到式（16）傳遞函數GY，GX，可以求取導彈偏航和滾轉通道的穩定裕度。

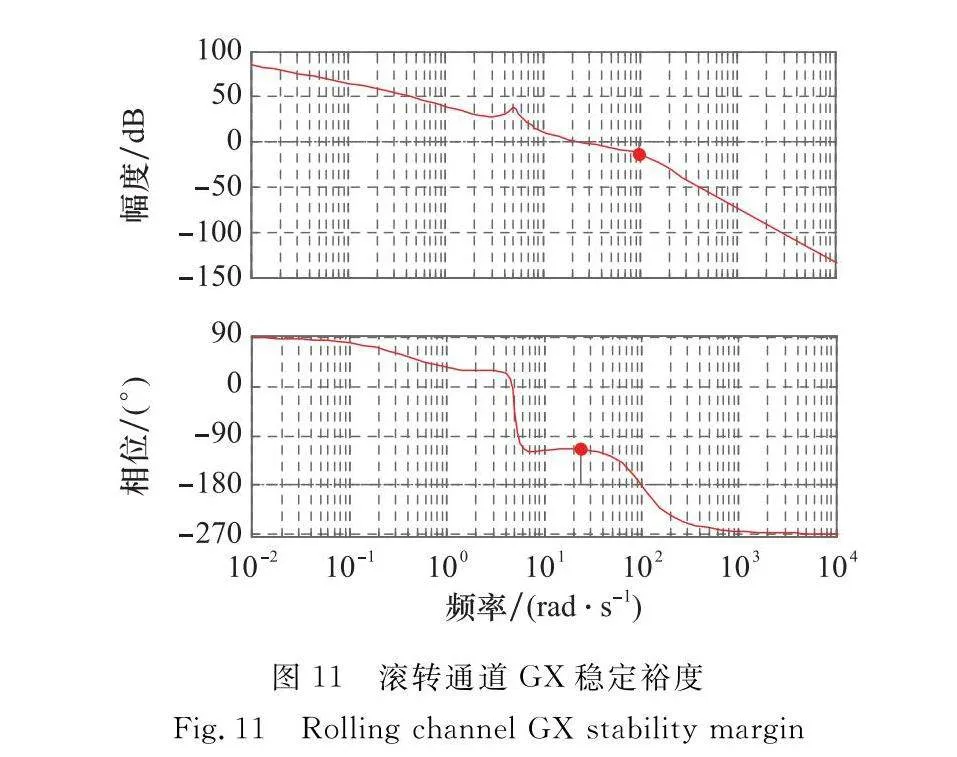
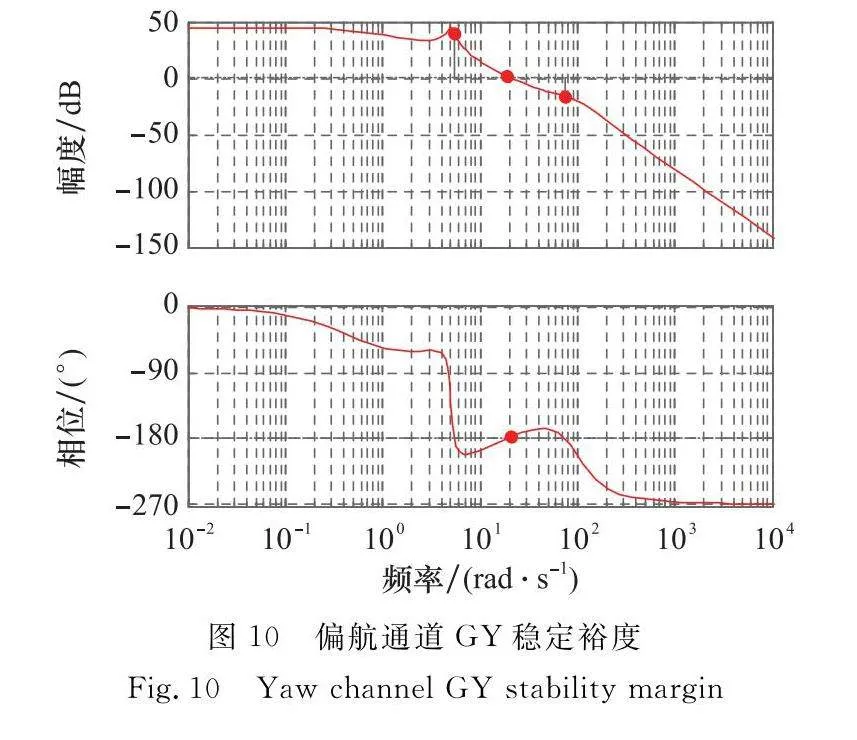
偏航通道GY穩定裕度如圖10所示。滾轉通道GX穩定裕度如圖11所示。

由圖10系統的穩定裕度可知，系統已失穩，但是此時時域響應結果表示系統依舊穩定收斂，因此可表示該傳遞函數對系統的描述不合理，具體數值將在表2中呈現。

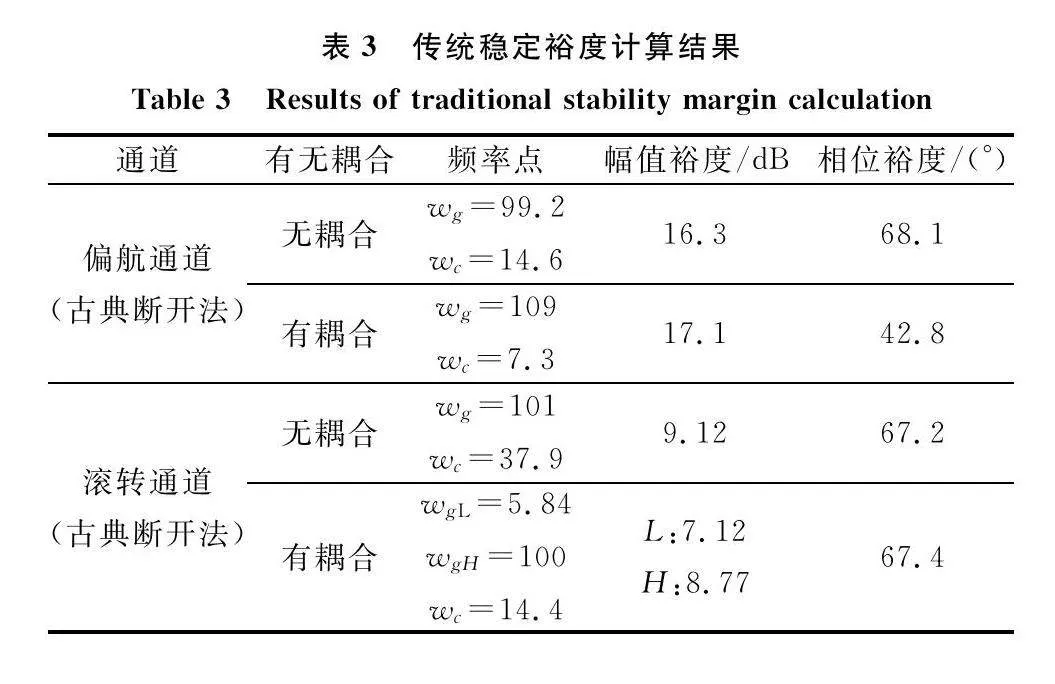
由上述仿真計算結果，為便于比較，將所有數據進行匯總，具體如表2和表3所示。

從表2數據可以看出：改進回差矩陣奇異值法所計算的穩定裕度比傳統回差矩陣奇異值法計算的穩定裕度要大，更加精確。回差陣奇異值方法計算穩定裕度時通過式（9）系統穩定的充分條件計算得到了穩定裕度，式（9）右邊代表系統的最小奇異值。從物理層面來看，距離原點距離越近表示系統穩定性越差，穩定裕度越小，而回差陣最小奇異值是以系統穩定性最差的點到達原點的距離描述系統穩定裕度，因此計算的穩定裕度具有一定保守性。另外，通過回差陣直接建立了幅值裕度和相位裕度之間關聯關系，二者是在同一頻率點下確定出來的;古典斷開法的幅值裕度處的頻率和相位裕度處的頻率不同。

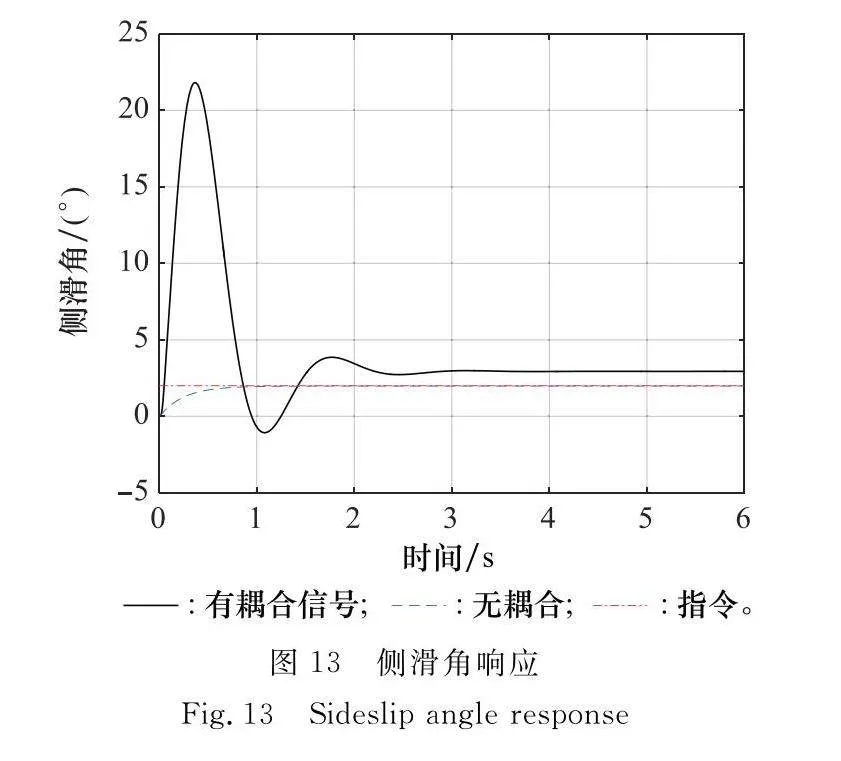
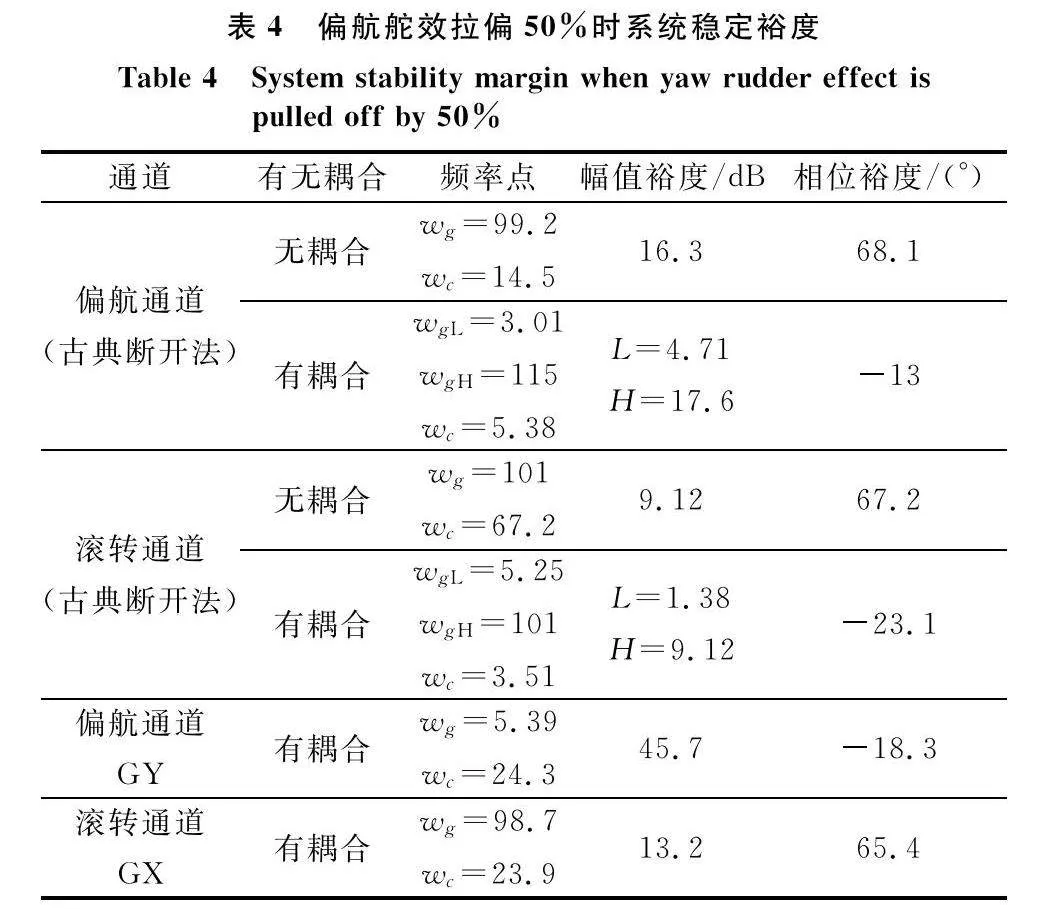
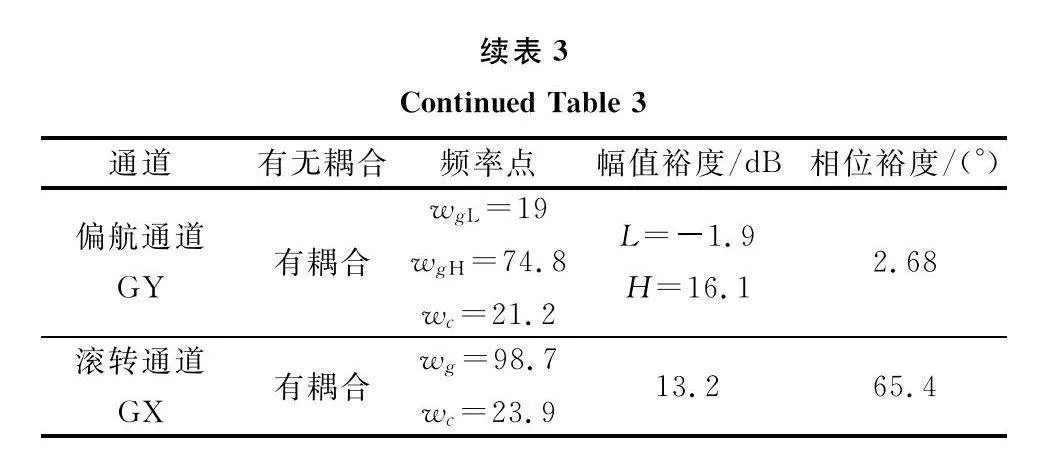
表3中，w_gL為低頻相角穿越頻率，w_gH為高頻相角穿越頻率，w_c為幅值穿越頻率。從表3數據可以看出：① 考慮耦合作用后，偏航通道相位裕度減小了25.3°，相較于耦合對相位裕度影響較大而言，耦合對兩通道幅值裕度影響較小;② 式（16）計算的系統穩定裕度為2.68°，表示系統不穩定，但系統的時域中系統響應依舊穩定收斂，如圖12和圖13所示。這表明兩處斷開計算系統穩定裕度較為保守，而式（17）計算的系統開環傳遞函數對系統描述更精確。為進一步驗證式（17）計算的系統穩定裕度比式（16）計算的系統穩定裕度更精確，將系統模型的偏航舵進行拉偏，如表4所示。

拉偏50%后系統偏航與滾轉通道時域響應發散，此時式（17）計算的穩定裕度也為負，系統時域響應曲線與頻域分析結果一致，這進一步表明式（17）描述的系統傳遞函數能更合理地表示系統穩定裕度，而且由于單處斷開耦合通道視為內回路，使得兩通道關聯性更強，拉偏偏航舵效后偏航通道不穩定進而導致滾轉通道發散，因此兩通道穩定裕度都為負。而斷開兩處時僅偏航通道受影響，滾轉通道裕度并未變化，這也進一步表示單處開計算穩定裕度更合理，也證明了式（17）對應的改進回差矩陣所計算的穩定裕度更精確。

4.3 通道耦合對控制品質的影響

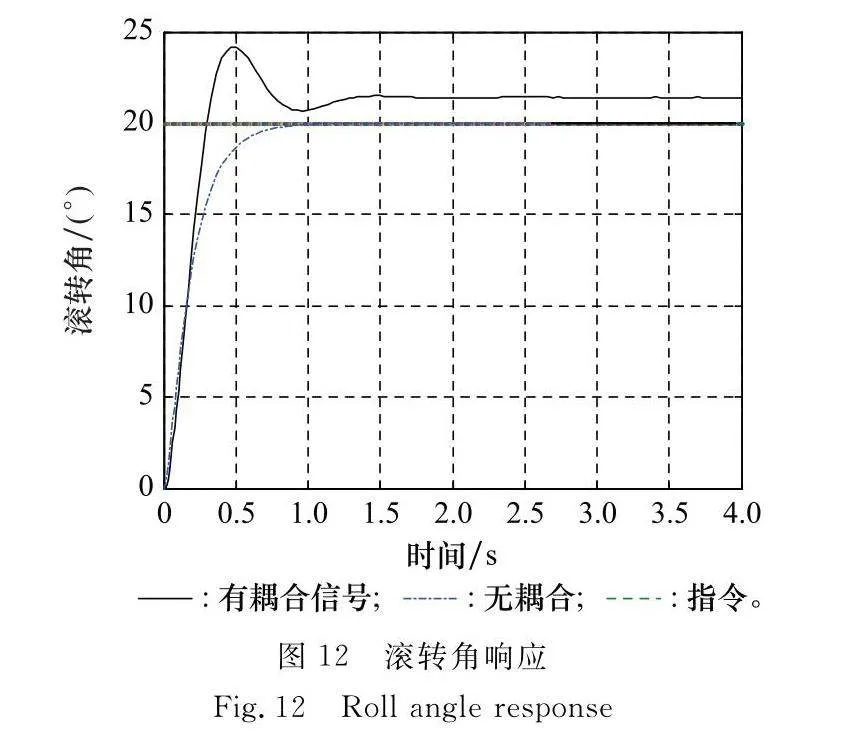
前面分析了系統耦合對系統的穩定裕度有較大影響，本節將進一步通過仿真分析通道耦合對系統的控制品質的影響。為更清楚看到耦合對系統的影響，將結構圖中的側滑角指令設為2°，滾轉角指令設為20°，滾轉角從0°至20°控制系統控制器參數取式（19），得到仿真結果如圖12和圖13所示。

由仿真結果可以看出，側向通道耦合使得滾轉角在跟蹤指令時有較大的超調，而且控制精度降低，因此需要設計相對應的解耦控制器實現解耦控制，提高穩定裕度和控制精度。

5 結 論

本文首先基于回差陣奇異值概念推導多變量系統的穩定裕度;而后以單通道和雙通道為例，分析表明傳統從舵系統環節前斷開和狀態空間描述下求取的開環傳遞函數結果一致。進一步，研究了雙通道控制模式下，單通道斷開、耦合通道視為內回路的新傳遞函數矩陣方法，并引入回差陣最小奇異值方法計算系統穩定裕度。通過仿真將傳統奇異值法和基于新傳遞函數矩陣的奇異值改進法計算出的穩定裕度、單通道穩定裕度、雙通道斷開的穩定裕度和基于通道耦合下的穩定裕度結合橫側向系統的時域響應進行對比分析，結果表明改進回差矩陣奇異值方法計算結果更精確，相較于斷開兩處的系統開環傳遞函數，斷開一處的基于通道耦合下的開環傳遞函數計算穩定裕度更合理。

參考文獻

［1］李帆， 周鳳岐， 周軍. 大迎角下導彈氣動耦合控制系統分析［J］. 飛行力學， 2001， 19（1）： 63-66.

LI F， ZHOU F Q， ZHOU J. Analysis of missile aerodynamic coupling control system at high angle of attack［J］. Flight Mechanics， 2001， 19（1）： 63-66.

［2］盧京潮. 自動控制原理［M］. 西安： 西北工業大學出版社， 2009.

LU J C. Automatic control principle［M］. Xi’an： Northwestern Polytechnical University Press， 2009.

［3］AL-SHAMALIS， JI B W， CRISALLE O D， et al. The Nyquist robust sensitivity margin for uncertain closed-loop systems［J］. International Journal of Robust and Nonlinear Control， 2005， 15（14）： 619-634.

［4］魏明英. 遠程防空導彈飛行控制方法研究［M］. 北京： 中國宇航出版社.

WEI M Y. Research on flight control methods of long-range air defense missiles［M］. Beijing： China Astronautics Publishing House.

［5］瞿福存， 史忠科， 戴冠中. MIMO系統穩定裕度的幾個定義［J］. 飛行力學， 2002， 2（2）： 6-9.

QU F C， SHI Z K， DAI G Z. Several definitions of stability margin for MIMO systems［J］. Flight Dynamics， 2002， 2（2）： 6-9.

［6］SKOGESTAD S， POSTLETHWAITE I. Multivariable feedback control： analysis and design［M］. New York： Wiley， 2007.

［7］吳斌， 程鵬. 多變量飛控系統的穩定裕度分析［J］. 航空學報， 1998， 19（6）： 657-661.

WU B， CHENG P， Stability margin analysis of multivariable flight control system［J］. Acta Aeronautica et Astronautica Sinica， 1998， 19（6）： 657-661.

［8］BAR-ON J R， ADAMS R J. Multivariable gain and phase margin analysis of a fully coupled six-degree-of-freedom guided missile［C］∥Proc.of the IEEE International Conference on Control Applications， 1999： 152-157.

［9］WILSON A， AMOLD W F. Multivariable stability margin for real uncertain parameters using Gerschgorin discs［C］∥Proc.of the AIAA Guidance， Navigation and Control Conference， 1991： 1486-1489.

［10］侯振乾. 參數不確定飛行器控制系統魯棒穩定性評估方法研究［D］. 西安： 西北工業大學， 2015.

HOU Z Q. Research on robust stability evaluation method for aircraft control system with uncertain parameters［D］. Xi’an： Northwestern Polytechnical University， 2015.

［11］WANG Q G， LI P W. Effective computation of all stabilizing gain and delay regions for MIMO systems［C］∥Proc.of the IEEE 14th International Conference on Control and Automation， 2018： 800-804.

［12］SEIFERTH D， AFONSO R， HELLER M， et al. Reduced conservatism proof of the balanced MIMO gain and phase margins［C］∥Proc.of the 59th IEEE Conference on Decision and Control， 2020： 905-911.

［13］LEHTOMAKI N A， SANDELL N R， ATHANS M. Robustness resuits in linear-quadratic Gaussian based multi-variable control designs［J］. IEEE Trans.on Automatic Control， 1981， 26（1）： 75-92.

［14］MUKHOPADHYAY V， NEWSOM J R. Application of matrix singular value properties for evaluating gain and phase margins of muti-loop systems［C］∥Proc.of the AIAA Guidance Navigation and Control Conference， 1982： 420-428.

［15］阮仕龍， 董哲， 孫堯， 等. 基于奇異值方法的推力矢量/氣動舵飛機復合控制律參數優化方法研究［J］. 北京航空航天大學學報， DOI： 10.13700/j.bh.1001-5965.2023.0227.

RUAN S L， DONG Z， SUN Y et al. Research on parameter optimization method of thrust vector/pneumatic rudder composite control law for aircraft based on singular value method［J］. Journal of Beijing University of Aeronautics and Astronautics， accepted， DOI： 10.13700/j.bh.1001-5965.2023.0227.

［16］HAO Z Y， ZHANG Q Y， CHEN H J， et al. Research and design of coordinated control strategy for smart electromechanical actuator system［J］. Transactions of Nanjing University of Aeronautics and Astronautics， 2022， 39（5）： 507-520.

［17］李信棟， 茍興宇. 基于天線驅動組件的多體衛星MIMO控制及穩定裕度應用研究［J］. 空間控制技術與應用， 2014， 40（2）： 20-25.

LI X D， GOU X Y. Application research on MIMO control and stability margin of multi-body satellite based on antenna driver module［J］. Space Control Technology and Application， 2014， 40（2）： 20-25.

［18］DOYLE J. Analysis of feedback systems with structured uncertainties［J］. Control Theory and Applications， 1982， 129（6）： 242-250.

［19］段子帆， 寧國棟， 張紅文， 等. 高超聲速飛行器橫航向MIMO系統控制及穩定裕度評估［J］. 戰術導彈技術， 2018（2）： 70-79.

DUAN Z F， NING G D， ZHANG H W， et al. Control and stability margin evaluation of transverse heading MIMO system for hypersonic vehicle［J］. Tactical Missile Technology， 2018（2）： 70-79.

［20］高黛陵， 吳麒. 多變量頻率域控制理論［M］. 北京： 清華大學出版社， 1998.

GAO D L， WU Q. Multivariable frequency domain control theory［M］. Beijing： Tsinghua University Press， 1998.

［21］HORN R A， JOHNSON C R. Matrix analysis second edition［M］. Beijing： Posts and Telecom Press， 2020.

［22］李奔. 線性系統PID參數穩定域研究［D］. 南京： 南京理工大學， 2010.

LI B. Research on the stable domain of PID parameters for linear systems［D］. Nanjing： Nanjing University of Science and Technology， 2010.

作者簡介

閆帥豪（1998—），男，碩士研究生，主要研究方向為飛行器穩定控制。

錢 瑞（1997—），女，工程師，碩士，主要研究方向為飛行器穩定控制。

魏明英（1966—），女，研究員，碩士，主要研究方向為飛行器總體設計、制導控制。

鄭勇斌（1978—），男，研究員，碩士，主要研究方向為導航、制導和控制。