基于編碼矩陣估計的極化碼參數盲識別算法

摘 要：

針對當前極化碼參數識別算法缺少對碼字起點的識別以及識別信息位算法計算復雜的問題，提出一種基于編碼矩陣估計的極化碼參數盲識別算法。所提算法首先將截獲的碼字矩陣、相應碼長下的克羅內克矩陣以及逆向重排矩陣相乘得到編碼矩陣估計，然后通過編碼矩陣的分布特征識別出碼長和碼字起點，最后使用訓練好的卷積神經網絡對極化碼信息位以及凍結位進行識別。實驗結果表明，所提方法不僅完成了碼字起點的識別，而且在未知碼字起點的情況下完成了對碼長的識別，且碼長的識別準確率優于現有算法，誤比特率在0.19時，參數為（32，12）的極化碼碼長識別率仍然可以達到90%以上。

關鍵詞：

極化碼; 參數盲識別; 編碼估計矩陣; 神經網絡

中圖分類號：

TN 911.7

文獻標志碼： A""" DOI：10.12305/j.issn.1001-506X.2024.09.33

Blind identification algorithm for polarization code parameters based on encoding matrix estimation

ZHANG Tianqi， YANG Zongfang*， ZOU Han， MA Kunran

（School of Communication and Information Engineering， Chongqing University of

Postsand Telecommunications， Chongqing 400065， China）

Abstract：

In order to solve the problem that the current polarization code parameter recognition algorithm lacks the recognition for the starting point of code word and the information bit recognition algorithm is complicated， a polarization code parameter blind recognition algorithm based on the code matrix estimation is proposed. The proposed algorithm firstly multiplies the intercepted codeword matrix with the Kronecker matrix under the corresponding code length and the reverse rearrangement matrix to obtain the code matrix estimation， then identifies the code length and the code word starting point by the distribution characteristics of the code matrix， and finally uses the trained convolutional neural network to identify the information bits and freezing bits of the polarization code. The experimental results show that the proposed method not only realizes the recognition for the starting point of code word， but also realizes the code length recognition when the code word’s starting point is unknown， and the code length recognition accuracy is better than the existing algorithm. When the bit error rate is 0.19， the polarization code length recognition rate of parameter （32，12） can still reach more than 90%.

Keywords：

polarization code; parameter blind identification; encoding estimation matrix; neural network

0 引 言

信道編碼是無線通信的重要組成部分，信道編碼技術能夠有效提升信號傳輸的質量，被廣泛應用到各種數字通信場景中。極化碼作為新型的信道編碼技術，是已知的唯一一種能夠被嚴格證明達到香農容量的信道編碼方式［1］。目前，第3代合作伙伴計劃（3rd generation partnership project， 3GPP）確定了以極化碼作為增強移動寬帶場景的控制信道編碼方案［2］。當前，信道編碼的盲識別問題已經成為自適應編碼調制技術和非合作通信領域的熱點研究問題，從當前已公開發表的文獻來看，現在大多數關于信道編碼參數識別的研究主要集中在循環碼［3-4］、卷積碼［5-6］、低密度奇偶校驗碼［7-8］（low density parity check， LDPC）和Turbo碼［9-10］，而對極化碼參數識別的研究較少，因此對于極化碼的參數識別研究也成為了一個亟待解決的問題。

極化碼屬于線性分組碼，也可以使用秩準則方法［11-12］對極化碼進行參數識別，但是這種方法計算復雜，而且抗噪性能差。文獻［13］利用監督矩陣和碼字矩陣之間的校驗關系對極化碼參數進行識別，但該方法在高誤碼率下的識別效果并不理想。文獻［14］引入對數似然比來檢測碼字與疑似校驗向量的校驗關系，估計出碼率及信息比特位置，該方法利用到了極化碼的碼字特征，但是仍然需要復雜的校驗檢測過程。文獻［15］則利用信息矩陣的分布特征完成極化碼碼長、信息位數和信息位位置的識別，識別效果也有所提升，但是仍然需要復雜的門限選取和檢測過程。文獻［16］提出一種高效的盲識別算法，該方法不需要遍歷所有的待識別碼長，只需要設定可能的最大碼長，就能夠完成極化碼參數識別。文獻［17］則在此基礎上，在不降低識別性能的前提下，除了完成對信息比特位置、碼長和碼率的識別，還完成對凍結比特位取值的識別。文獻［18］通過計算軟輸出序列所提出的奇偶校驗一致性來識別極化碼的碼長、碼率和凍結位位置，相比現有方法復雜度更低。文獻［19］提出一種新的加性高斯白噪聲信道下的極化碼參數識別方案，該方案能夠有效識別極化碼的各類參數。文獻［20］則通過深層神經網絡對極化碼種類進行5種極化碼的閉集識別。目前，還未出現使用神經網絡對極化碼進行參數識別的研究，因此本文考慮將神經網絡用于極化碼參數識別。

以上算法雖然都能夠有效識別極化碼的碼長、碼率等參數，但都默認預先知道所截獲極化碼序列的碼字起點，并且這些方法都使用到了復雜的校驗檢測過程。針對上述問題，本文提出一種基于編碼估計矩陣的極化碼參數盲識別算法，在未知碼字起點的情況下，該算法首先構造不同碼長和碼字起點下的碼字矩陣，再通過碼字矩陣與估計碼長下的克羅內克矩陣以及逆向重排矩陣相乘得到編碼矩陣估計，然后利用編碼矩陣估計的元素分布特征來識別極化碼碼長以及正確的碼字起點，最后在識別信息位長度和信息位位置時，該算法也不再使用復雜的校驗檢測過程，而是將不同碼長和碼率下對應的正確編碼矩陣中的凍結比特所在列和信息比特所在列送入到卷積神經網絡（convolutional neural network，CNN）中進行訓練，并將訓練收斂的網絡模型作為信息位及凍結位的識別器，最后將待識別編碼估計矩陣中的列送入識別器中進行識別，就可以判斷出該列的索引是否為信息位，至此就完成極化碼的參數識別。

1 極化碼基礎

極化碼是通過引入信道極化的理論［1］而建立的。信道極化分兩個階段，分別是信道聯合和信道分裂。通過信道的聯合和分裂，各個子信道的對稱容量將呈現兩極分化的趨勢：隨著碼長N的增加，一部分子信道的容量趨于1，稱為信息子信道，而其余子信道的容量趨于0，稱為凍結子信道。極化碼正是利用這一信道極化現象，在容量趨于1的K個子信道上傳輸信息比特，在其他子信道上傳輸凍結比特（即收發雙方已知的固定比特，通常設置為全零）。由此構成的信道編碼即為極化碼，碼率為K/N。

2.3 參數識別步驟

步驟 1

碼長識別：首先通過不同估計碼長以及該碼長下所有碼字起點構造碼字矩陣，然后將該碼字矩陣乘以對應碼長下的克羅內克積矩陣和逆向重排矩陣得到編碼矩陣估計E^e，然后求每一個E^e的γ值，再找到每一個估計碼長下不同碼字起點對應的最小γ值，將其作為該估計碼長下待選的γ值，最后由這些待選的γ值求出不同估計碼長下的歸一化差分值d，最小d值對應的估計碼長Ne即為真實碼長Nt。

步驟 2

碼字起點識別：在經步驟1求得正確碼長的情況下，根據該碼長構造不同碼字起點下的碼字矩陣，求其對應的編碼矩陣估計E^e，求出每一個碼字起點對應的γ值，再根據γ值求出不同估計碼字起點下的d值，最后找到最大d值對應的估計起點l+1，求出的l即為正確的碼字起點。

步驟 3

信息位長度及位置識別：在經步驟1和步驟2得到正確碼長和碼字起點的情況下，構造正確的碼字矩陣，再根據碼字矩陣得到真實的編碼矩陣，然后將編碼矩陣列向量送入預先訓練好的CNN中進行識別，得到信息列和凍結列，識別出的信息列個數就是信息位長度，信息列的列索引就是信息位位置。

3 仿真實驗及分析

3.1 碼長識別實驗

本節實驗采用了極化碼參數為（32，12）、（128，60）、（512，250）的3種極化碼進行分析，在BEC信道中進行傳輸，截獲的碼字組數為300。在未知碼字起點的情況下，遍歷所有碼長求出d值，再根據d值求出待識別碼長。誤比特率為0.04時的碼長識別結果如圖2所示。

由圖2可知，在未知碼字起點時，遍歷所有碼長求出的歸一化差分值達到最小時對應的碼長即為正確的估計碼長，這與之前的分析一致。分析圖2（b）可知，當碼長指數n=7時，歸一化差分值達到最小，此時對應的碼長Ne=128即為真實碼長Nt，當Nelt;Nt時，隨著Ne的增大，歸一化差分值會出現減小的趨勢，直至Ne=Nt時達到最小;當Ne=2Nt時，歸一化差分值會有一個較大的增加，并且在Negt;Nt區間內歸一化差分值相差不大，在一定范圍內波動。

3.2 碼字起點識別仿真實驗

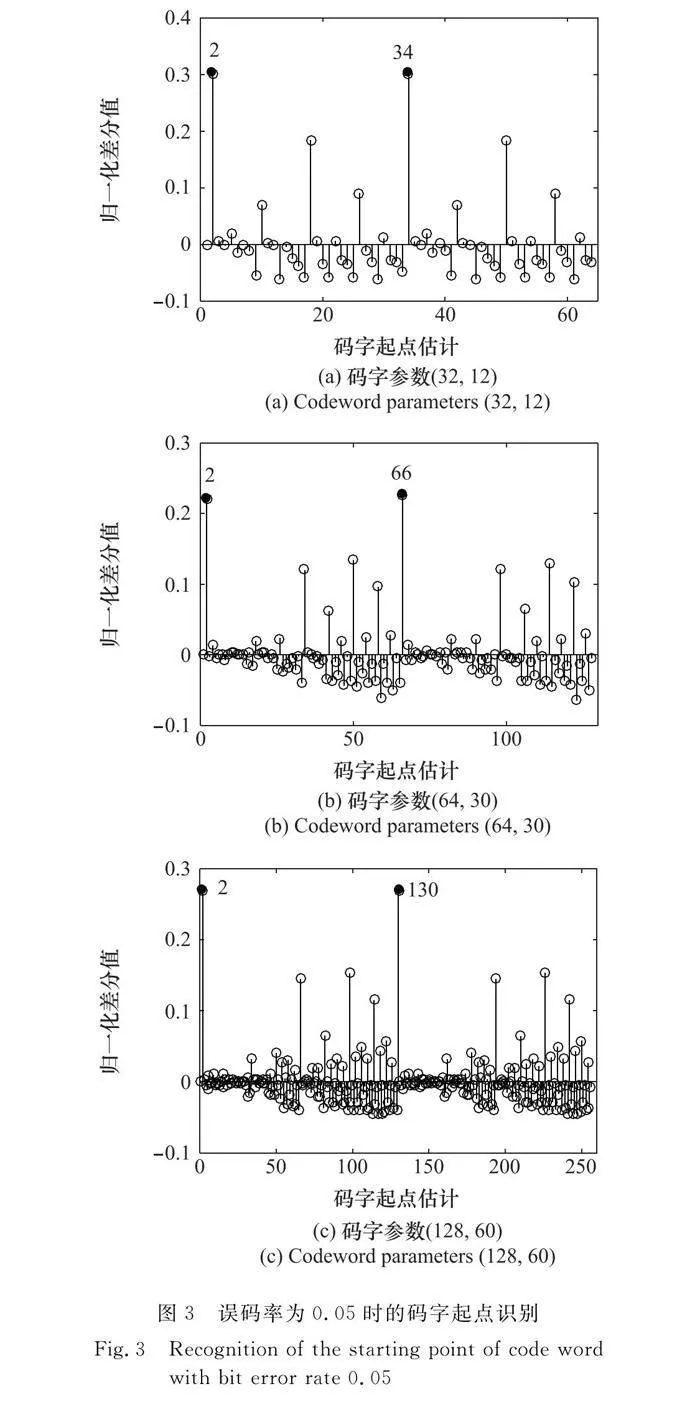
本節實驗采用的極化碼碼字參數為（32，12）、（64，30）和（128，60），截獲的碼字組數為500。在求出正確的碼長后，遍歷Nt個碼字起點對應的編碼估計矩陣，求出不同碼字起點下的歸一化差分值，對碼字起點進行識別。圖3為了便于分析，給出了2Nt個碼字起點下的歸一化差分值。

由圖3可知，在正確的碼長下，遍歷所有碼字起點求出的歸一化差分值達到最大時對應的估計起點減1即為正確的碼字起點。如圖3（b）所示，當碼字起點估計等于2和66時，歸一化差分值達到最大，而將這兩個碼字起點估計減1后得到的1和65剛好就是第1個碼長周期下和第2個碼長周期下的碼字起點。此時從這兩個碼字起點位置截獲碼長為64的比特流序列來構建的碼字矩陣即為正確的碼字矩陣。

3.3 性能分析

實驗 1

不同碼長對識別性能的影響

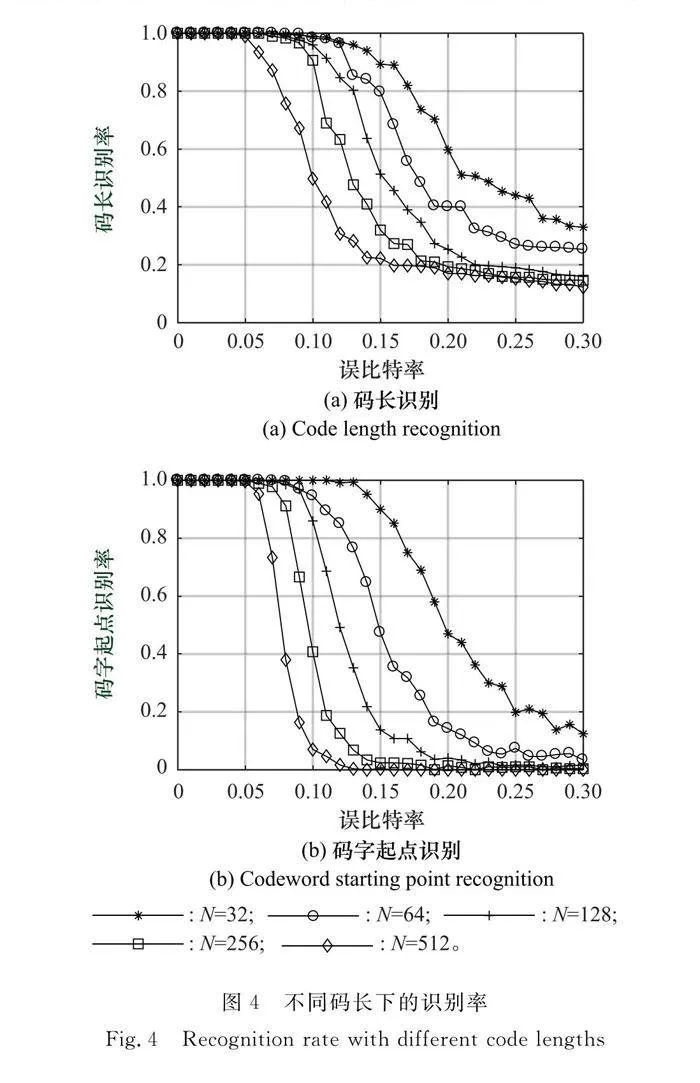
本實驗選取了固定碼率為1/2的5種碼長（N分別取32、64、128、256、512）的極化碼碼長及碼字起點進行識別，碼字組數為300，進行500次蒙特卡羅實驗，碼長和碼字起點識別率隨著誤比特率升高而變化，變化曲線如圖4所示。

從圖4可以看出，在相同誤碼率下，碼長為32時極化碼碼長和碼字起點識別率在5種碼字中是最高的。碼長越小，識別率越高，隨著碼長的增加，識別性能會逐漸降低。這是因為極化碼碼長越長，碼字矩陣中誤碼的個數越多，這會導致編碼估計矩陣中的元素分布更隨機，對識別率影響也就較大。整體而言，對不同碼長下的極化碼碼長及碼字起點都能夠進行有效識別。對于碼長為256的極化碼，碼長識別率在誤比特率為0.1時仍然能夠達到90%以上，碼字起點識別率在誤比特率為0.08時也能夠達到90%以上。

實驗 2

不同信息位長度對識別性能的影響

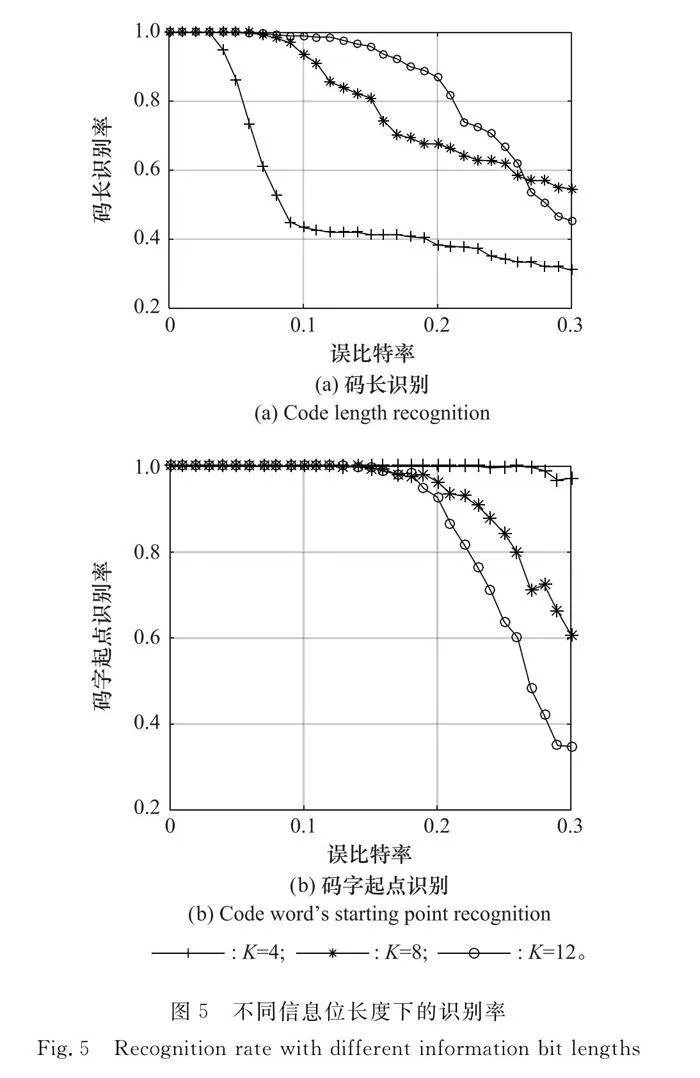
本實驗選取了固定碼長為32的3種信息位長度（K分別取4、8、12）的極化碼碼長進行識別，碼字組數為300，進行500次蒙特卡羅實驗，碼長和碼字起點識別率如圖5所示。

從圖5（a）和圖5（b）可以看出，信息位長度為4時碼字起點識別效果最好，信息位為12時碼長識別效果最好，并且隨著信息長度增加，碼長識別效果越來越好，碼字起點效果逐漸變差。出現這種情況的原因是隨著信息位的增大，編碼矩陣估計中元素“1”所占的比例也隨之增大，而凍結位所占的比例降低。誤碼率一旦過大，就會有大量的凍結位元素變為1，這就會導致編碼矩陣估計求出的γ值相差不大，因此信息位越小，碼字起點的識別效果越好。

實驗 3

信息位位置及長度識別實驗

（1） 信息位識別器：首先根據圖1和表1中的CNN結構和參數來構造信息位識別器。

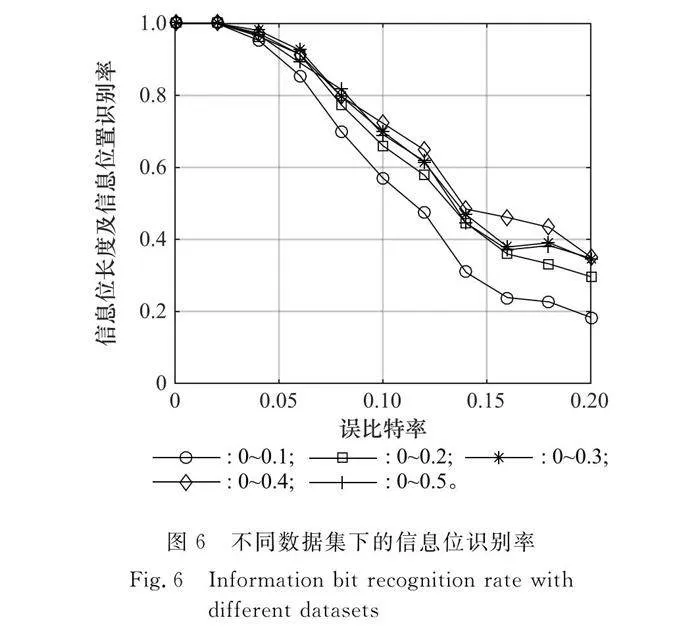
（2） 構造數據集：通過設置不同誤碼率下的數據集對（32，12）、（64，32）、（128，60），在這3種參數的極化碼編碼矩陣估計的列向量打上標簽并進行訓練，本文中不同誤碼率數據集的選取范圍為0～0.1、0～0.2、0～0.3、0～0.4、0～0.5，步長為0.01。隨后，對不同數據集下訓練后的模型進行測試，圖6為5種數據集下的測試結果。

從圖6的測試結果可以看出，0～0.1誤碼率的數據集識別效果最差，其他4種數據集識別效果比較接近，但0～0.3誤碼率的數據集在低誤比特率時效果最好，因此本文選取誤碼率為0～0.3時的數據集進行訓練。

（3） 對信息位位置和長度的識別，本文采用的測試集也是（32，12）、（64，32）、（128，60）這3種參數下的極化碼，碼字組數為500。訓練集生成各個誤碼率下的每種碼字的編碼估計矩陣為1 000個，共93 000個樣本，測試集選取其中的1/2。不同算法的信息位長度及位置平均識別率對比如圖7所示。

從圖7中本文方法和文獻［15］方法這3種碼字的平均識別率對比可以分析得出，本文采用的神經網絡方法要優于文獻［15］提出的信息矩陣分析法。本文將凍結列和信息列送入CNN中進行識別，利用信息列和凍結列之間的差異，不再需要求出信息位和凍結位之間的門限，碼長及碼率對信息位識別性能沒有影響，信息位識別性能只和信息列、凍結列之間的差異有關，所以對比平均識別概率，本文方法要優于文獻［15］方法，在誤碼率為0.08時，仍然能夠達到80%以上的識別率。

實驗 4

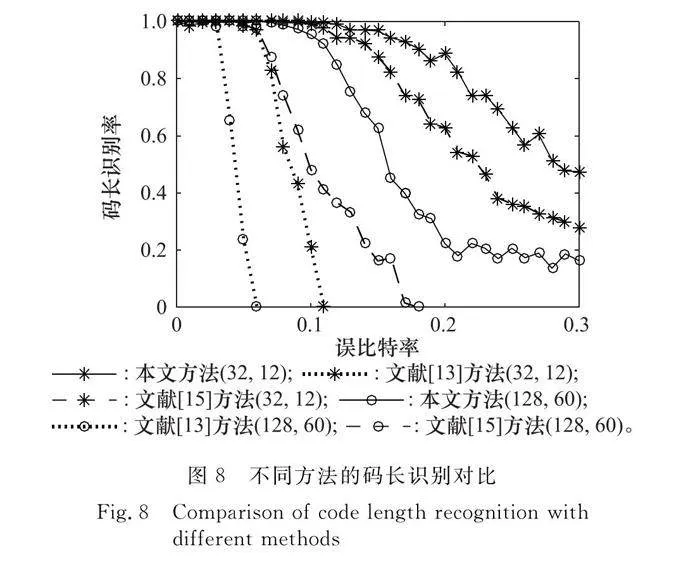
碼長識別對比實驗

本實驗選取了兩種參數為（32，12）、（128，60）的極化碼進行分析，碼字組數為200，蒙特卡羅實驗次數為500，對比結果如圖8所示。

分析圖8可知，本文方法可以在未知碼字起點的情況下有效識別不同參數的極化碼碼長，而且從參數（32，12）和（128，60）的識別曲線可知，本文方法的識別性能要優于現有已知碼字起點的識別算法。這是由于在進行碼長識別時，本文算法直接使用編碼矩陣的歸一化矩陣重量，相比文獻［15］中的零均值更加精確，而且由于沒有矩陣映射的過程，算法復雜度要更低一些。對參數為（32，12）的極化碼碼字識別而言，在誤比特率為0.21的情況下，碼長識別率能夠達到80%以上。對參數為（128，60）的極化碼碼字，在誤比特率為0.12的情況下，碼長識別率也能夠達到80%以上。

3.4 算法計算復雜度分析

假設已經求得正確的碼字起點，截獲的極化碼碼字比特流的長度為L，遍歷的碼長為2n（nmin≤n≤nmax）。本文算法的計算復雜度主要集中于構造編碼矩陣和計算歸一化編碼矩陣重量。由于需要對所有估計碼長進行編碼矩陣估計，需要構造nmax－nmin個編碼矩陣，單獨構造1個編碼矩陣時需要進行L/2n22n次乘法運算和L/2n2n（2n－1）次加法運算。計算歸一化編碼矩陣重量時需要進行1次乘法運算和L/2n－1（2n－1）次加法運算。因此，本文算法整體需進行∑nmaxn=nminL/2n22n+1次乘法運算和∑nmaxn=nminL/2n22n－L/2n－2n+1次加法運算。

文獻［15］的計算復雜度主要集中在構造分析矩陣以及求解零均值比部分，其算法整體需要進行∑nmaxn=nminL/2n22n+L/2n2n+2次乘法運算和∑nmaxn=nminL/2n22n+L/2n2n－L/2n－2n+1次加法運算。綜上所述，本文算法的計算復雜度更低，且在碼長范圍較小時更為明顯。

4 結 論

本文首先根據極化碼編碼矩陣的性質，給出極化碼參數識別的3個定理并加以證明，然后利用這些定理提出了極化碼的參數識別方法。在未知碼字起點的情況下，能夠識別出極化碼的碼長，并且能夠根據正確識別的碼長對碼字起點進行估計，然后使用CNN對編碼矩陣中的信息列和凍結列進行識別，求出信息位長度以及位置分布。與其他算法相比，本文算法不僅可在未知碼字起點時識別出極化碼碼長，對碼長的識別效果更好，并且也識別出正確的碼字起點，在識別信息位長度及位置時也舍去了復雜的校驗檢測過程，且信息位長度及位置的平均識別率要優于現有算法，在實際工程中有良好的應用前景。

參考文獻

［1］ ARIKAN E. Channel polarization： a method for constructing capacity-achieving codes for symmetric binary-input memoryless channels［J］. IEEE Trans.on Information Theory， 2009， 55（7）： 3051-3073.

［2］ GAMAGE H， RAJATHEVA N， LATVA-AHO M. Channel coding for enhanced mobile broadband communication in 5G systems［C］∥Proc.of the European Conference on Networks and Communications， 2017.

［3］ 張曉林， 李修橋， 孫溶辰. 基于快速碼根檢驗的RS碼綜合識別算法［J］. 通信學報， 2022， 43（11）： 117-126.

ZHANG X L， LI X Q， SUN R C. Comprehensive recognition algorithm for RS codes based on fast root check［J］. Journal of Communications， 2022， 43（11）： 117-126.

［4］ 吳昭軍， 張立民， 鐘兆根， 等. 低信噪比下循環碼識別［J］. 電子學報， 2020， 48（3）： 478-485.

WU Z J， ZHANG L M， ZHONG Z G， et al. Cyclic code recognition with low signal-to-noise ratio［J］. Acta Electronica Sinica， 2020， 48（3）： 478-485.

［5］ 陳增茂， 陸麗， 孫志國， 等. 基于共軛梯度求解代價函數的卷積碼參數識別算法［J］. 系統工程與電子技術， 2022， 44（10）： 3235-3242.

CHEN Z M， LU L， SUN Z G， et al. Convolutional code para-meter recognition algorithm based on conjugate gradient solving cost function［J］. Systems Engineering and Electronics， 2022， 44（10）： 3235-3242.

［6］ 吳昭軍， 張立民， 鐘兆根， 等. 基于迭代消元的卷積碼快速識別［J］. 電子學報， 2021， 49（6）： 1108-1116.

WU Z J， ZHANG L M， ZHONG Z G， et al. Fast recognition of convolutional codes based on iterative elimination［J］. Acta Electronica Sinica， 2021， 49（6）： 1108-1116.

［7］ 王忠勇， 李正豪， 鞏克現， 等. 高誤碼率下基于隨機抽取的LDPC碼校驗矩陣重建［J］. 通信學報， 2023， 44（3）： 128-137.

WANG Z Y， LI Z H， GONG K X， et al. LDPC code verification matrix reconstruction based on random extraction under high bit error rate［J］. Journal of Communications， 2023， 44（3）： 128-137.

［8］ 劉倩， 張昊， 宋瑩炯， 等. 小樣本條件下基于矩陣乘法和秩分析的LDPC參數估計方法［J］. 電子學報， 2022， 50（5）： 1075-1082.

LIU Q， ZHANG H， SONG Y J， et al. LDPC parameter estimation method based on matrix multiplication and rank analysis under small sample conditions［J］. Acta Electronica Sinica， 2022， 50（5）： 1075-1082.

［9］ 胡延平， 張天騏， 白楊柳， 等. 刪余型Turbo碼分量編碼器盲識別算法［J］. 信號處理， 2021， 37（11）： 2207-2215.

HU Y P， ZHANG T Q， BAI Y L， et al. Type delete more than blind identification algorithm of Turbo code component encoder［J］. Journal of Signal Processing， 2021， 37（11）： 2207-2215.

［10］ 李卓倫， 韓卓茜. 利用多種糾錯方式進行優化的Turbo碼交織器識別［J］. 電子學報， 2021， 49（2）： 239-247.

LI Z L， HAN Z X. Turbo code interleaver recognition based on multiple error correction methods［J］. Acta Electronica Sinica， 2021， 49（2）： 239-247.

［11］ RAMABADRAN S， MADHU A， KUMAR S， et al. Blind re-cognition of LDPC code parameters over erroneous channel conditions［J］. IET Signal Processing， 2019， 13（1）： 86-95.

［12］ SHARMA A， PILLAI N R. Blind recognition of parameters of linear block codes from intercepted bit stream［C］∥Proc.of the International Conference on Computing， Communication and Automation， 2016： 1262-1266.

［13］ 張天騏， 胡延平， 馮嘉欣， 等. 基于零空間矩陣匹配的極化碼參數盲識別算法［J］. 電子與信息學報， 2020， 42（12）： 2953-2959.

ZHANG T Q， HU Y P， FENG J X， et al. Blind recognition algorithm of polarization code parameters based on 1 space matrix matching［J］. Journal of Electronics and Information Technology， 2020， 42（12）： 2953-2959.

［14］ 吳昭軍， 鐘兆根， 張立民， 等. 基于軟判決下的不刪余極化碼參數識別［J］. 通信學報， 2020， 41（12）： 60-71.

WU Z J， ZHONG Z G， ZHANG L M， et al. Parameter recognition of undeleted polarization code based on soft decision［J］. Journal of Communications， 2020， 41（12）： 60-71.

［15］ 劉鑒興， 張天騏， 柏浩鈞， 等. 基于信息矩陣估計的極化碼參數盲識別算法［J］. 系統工程與電子技術， 2022， 44（2）： 668-676.

LIU J X， ZHANG T Q， BAI H J， et al. Blind recognition algorithm of polarization code parameters based on information matrix estimation［J］. Systems Engineering and Electronics， 2022， 44（2）： 668-676.

［16］ 王垚， 王翔， 楊國東， 等. 基于編碼矩陣結構特征的非刪余極化碼參數盲識別算法［J］. 通信學報， 2022， 43（2）： 22-33.

WANG Y， WANG X， YANG G D， et al. Nondeleted polarization code parameter blind recognition algorithm based on coding matrix structure feature［J］. Journal of Communications， 2022， 43（2）： 22-33.

［17］ 王垚， 王聰， 王翔， 等. 一種基于軟判決的非刪余極化碼參數識別算法［J］. 系統工程與電子技術， 2023， 45（10）： 3293-3301.

WANG Y，" WANG C， WANG X， et al. Non-punctured polar code parameter recognition algorithm based on soft decision［J］. Systems Engineering and Electronics， 2023， 45（10）： 3293-3301.

［18］ LIU Q， ZHANG H， YU P D. Blind detection and identification of polar codes based on the parity check conformity［J］. IEEE Communications Letters， 2022， 26（4）： 728-732.

［19］ LIU H Y， WU Z J， ZHANG L M， et al. Polar code parameter recognition algorithm based on dual space［J］. Electronics， 2022， 11（16）： 2511.

［20］ DENG P， ZHANG T Q， WEN L H， et al. Blind identification algorithm of polar code based on convolutional neural network［EB/OL］. ［2023-05-04］.http：∥doi.org/10.23919/JCC.ja.2022-0453.

作者簡介

張天騏（1971—），男，教授，博士，主要研究方向為通信信號盲處理、神經網絡實現。

楊宗方（1998—），男，碩士研究生，主要研究方向為信道編碼盲識別技術。

鄒 涵（1998—），男，碩士研究生，主要研究方向為通信信號盲處理。

馬焜然（1999—），男，碩士研究生，主要研究方向為數字水印、信息隱藏。