超導超高壓同步調相機多工況下定子電磁力計算及強度分析

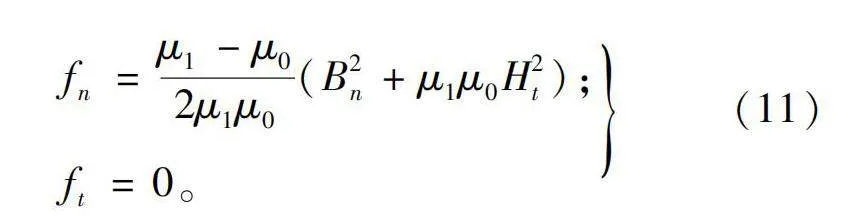
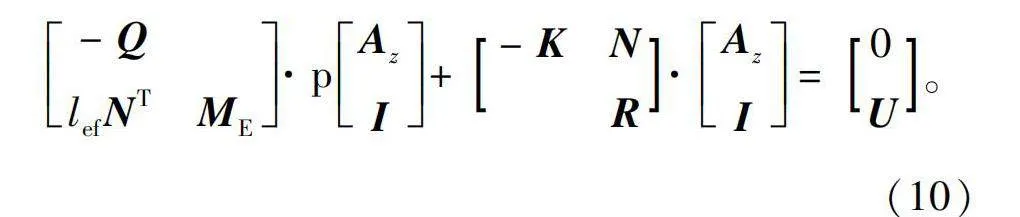
摘 要：超導調相機采用電纜繞組非磁性齒的高壓定子新結構（簡稱超導超高壓調相機），可實現調相機與電網的直連。針對超導超高壓調相機定子采用非磁性齒結構，導致齒部磁阻增加，槽漏磁增大，出現定子齒壁兩側受力不均以及繞組切向洛倫茲力增大的問題，構建了超導超高壓調相機無升壓變壓器與電網直連的場-路耦合數學模型，結合麥克斯韋應力法和洛倫茲力原理，計算了進相與遲相運行，短時深度進相與遲相運行4種運行工況下定子齒壁所受電磁力，并給出齒壁兩側電磁力隨時間以及空間的變化規律。將計算得到的電磁力作為載荷，對不同運行工況下定子齒的強度進行計算，得到了定子齒形變大小和應力分布規律。結果表明超導超高壓同步調相機在多種工況下運行時，非磁性定子齒不會發生疲勞斷裂現象。該研究為超導調相機采用非磁性定子齒及超高壓繞組結構提供理論依據。

關鍵詞：同步調相機；場路耦合；超高壓定子；非磁性定子齒；麥克斯韋應力法；強度分析

DOI：10.15938/j.emc.2024.10.004

中圖分類號：TM342

文獻標志碼：A

文章編號：1007-449X（2024）10-0034-12

收稿日期： 2023-09-27

基金項目：國網浙江省電力有限公司科技項目（B311DS22000L）

作者簡介：肖士勇（1988—），男，博士，講師，研究方向為大型發電設備及系統內部故障的模擬、診斷與保護；

張家樂（2001—），男，碩士研究生，研究方向為大型同步電機電磁計算與分析；

戈寶軍（1960—），男，博士，教授，博士生導師，研究方向為大型機電能量轉換裝置的基礎理論與應用技術；

張建承（1988—），男，博士，研究方向為新型電力系統勵磁控制與機網協調技術。

通信作者：肖士勇

Stator electromagnetic force calculation and strength analysis of superconducting ultra high voltage synchronous condenser under multi-operating conditions

XIAO Shiyong¹， ZHANG Jiale¹， GE Baojun²， ZHANG Jiancheng³

（1.School of Electrical Engineering， Northeast Electric Power University， Jilin 132012， China;

2.School of Electrical and Electrical Engineering， Harbin University of Science and Technology， Harbin 150080， China；3.State Grid Zhejiang Electric Power Research Institute， Hangzhou 310014， China）

Abstract：Superconducting condenser adopts a new structure of high voltage stator with non-magnetic teeth of cable windings （referred to as superconducting ultra high voltage condenser）， which can realize the direct connection between the condenser and the power grid. For the superconducting ultra high voltage condenser， the stator adopts a non-magnetic teeth structure， which leads to the increase of teeth reluctance， the increase of slot leakage， the uneven force on both sides of the stator teeth wall， and the tangential Lorentz force of the winding of the condenser is increased. The field-circuit coupled mathematical model of superconducting ultra high voltage condenser without step up transformer directly connected to power grid was established. Based on Maxwell stress method and Lorentz force principle， the electromagnetic force on stator teeth wall under four operating conditions of leading and lagging power factor operating and short time deep leading and lagging power factor operating was calculated， and the variation of electromagnetic force on both sides of the teeth wall with time and space were given. Using the calculated electromagnetic force as the load， the strength of stator teeth under different operating conditions was calculated， and the deformation size and stress distribution of the stator teeth were obtained. The results show that the non-magnetic stator teeth will not break when the superconducting ultra high voltage synchronous condenser operates under various operating conditions. The research provides a theoretical basis for using non-magnetic stator teeth and ultra high voltage winding structure for superconducting condenser.

Keywords：synchronous condenser; field circuit coupled model; ultra high voltage stator; non-magnetic stator teeth; Maxwell stress method; strength analysis

0 引 言

相較于靜態無功補償方式，同步調相機對交流電網穩定性的支撐能力優勢明顯^［1］。目前，隨著電力系統低碳轉型的不斷推進，以及特高壓直流輸電網絡的大規模建設，動態無功功率支撐對維系電網的安全穩定運行至關重要。在此背景下，新型電力系統對調相機的無功響應速度及深度調相能力提出了更高的要求。

隨著材料的發展及技術的突破，研制新型同步調相機已成為一個重要研究方向。其中，超導超高壓同步調相機，提出將超導轉子與超高壓定子技術相結合。超導轉子可大幅提高調相機勵磁能力，在提高響應速度的同時為調相機深度調相運行提供了可能；超高壓定子采用交聯聚乙烯電纜作為定子繞組^［2-3］，可大幅度提高定子繞組的電壓等級，實現調相機與電網的直連，省去升壓變壓器減小了調相機與電網的聯系電抗，同時避免了變壓器的無功及有功消耗，可顯著提高調相機的無功響應速度及效率。綜上，超導超高壓調相機的調相性能滿足新型電力系統對無功功率的新需求，對提升新型電力系統的運行穩定性和可靠性意義重大。

由于超導超高壓同步調相機定子采用非磁性齒結構，導致齒部磁阻大幅增加，則槽漏磁增加。槽漏磁引起齒壁兩側磁場不對稱，則齒壁兩側電磁力分布不對稱。另外，槽漏磁導致調相機調相運行時繞組產生較大的洛倫茲力，且當電力系統電壓突變時，常要求調相機深度調相運行，短時無功功率接近額定功率的2倍左右^［4］，加之高壓定子非磁性齒細長，造成齒的強度降低。因此，對于采用高壓定子非磁性齒結構的超導調相機，開展其深度調相運行時新型齒槽結構的電磁力與強度的計算具有重要意義。

目前電磁力的計算主要有虛位移法和麥克斯韋應力法。文獻［5］對2種方法進行了比較，虛位移法可以較為簡單準確地計算電機整體受到的電磁力，麥克斯韋應力法可直接求得局部電磁力密度，但需要較高的網格精度，積分路徑上數值不連續可能對電磁力計算結果產生影響，因此使用時要關注積分路徑的選取。文獻［6］采用虛位移法推導了直線同步電機的牽引力計算公式，并將計算結果與有限元仿真結果進行比較，驗證了虛位移法計算電磁力的準確性。在電機動態電磁力及強度計算方面，國內外學者進行了詳細研究，文獻［7］采用麥克斯韋應力法研究了同步發電機定子繞組匝間短路時轉子上受到的動態電磁力。文獻［8］對水輪發電機中性點側，發生小匝數相間短路故障前后定子鐵心動態電磁力進行計算。文獻［9］對發電機額定并網運行時，變壓器高壓側一相斷開的非全相工況下，汽輪發電機轉子動態電磁力變化規律進行了研究。文獻［10］對定子支路不對稱汽輪發電機在正常運行、氣隙偏心、轉子匝間短路故障及氣隙偏心與轉子匝間短路復合故障下定子鐵心電磁力變化規律進行了研究。文獻［11］對橫向磁通永磁同步電機不同厚度轉子盤的機械強度進行了計算。文獻［12］研究了橫向磁通永磁同步電機不同運行工況下，轉子鐵心受電磁力作用發生形變大小和應力分布。文獻［13］對籠型感應電機轉子發生斷條故障前后，轉子所受電磁應力與結構靜力學進行了研究。除了對電機轉子側動態電磁力及強度進行分析，定子側相關方面研究則集中在端部繞組部分。文獻［14］對汽輪發電機的端部繞組電磁力密度進行了計算，得到了端部電磁力最大的部位，為后續研究提供參考。文獻［15］建立了大型汽輪發電機定子端部三維有限元模型，計算定子端部繞組在額定工況下受到的電磁力，并應用計算結果對端部結構進行了強度分析。分析發現，現有文獻未對調相機多工況下定子齒部電磁力及強度進行計算與分析，更未涉及超導調相機具有“細長型”非磁性齒結構情況下的電磁力分布規律研究與機械強度校核分析。

為此，本文首先建立超導超高壓同步調相機并網運行的場路耦合仿真模型，對調相機在遲相（過勵額定電流）、深度遲相（過勵2倍額定電流）、進相（欠勵額定電流）、深度進相（欠勵1.5倍額定電流，受調相機運行最小勵磁電流和定子端部散熱能力限制，深度進相運行取1.5倍額定電流）4種工況下的電磁性能進行了仿真分析。其次，以仿真得到的磁場數據為基礎，利用麥克斯韋應力法和洛倫茲力原理，對非磁性定子齒壁受到的電磁力進行計算，分析多工況下電磁力隨時間及空間的變化規律。最后建立非磁性定子齒的三維有限元模型，基于電磁力計算結果，對定子齒結構靜力學進行研究，得到非磁性定子齒在多工況下的應力分布和形變規律。

1 超導超高壓調相機模型及電磁力計算方法

1.1 超導超高壓同步調相機拓撲結構

超導超高壓同步調相機將轉子置于真空腔內，通過旋轉密封結構與外部冷卻結構和氦氣泵相連，使冷氦氣在封閉系統內循環，可實現超導環境，超導轉子具體結構參見文獻［16］。定子繞組采用絕緣電纜繞制，為避免齒部磁密過飽和造成鐵心損耗過高，定子采用非磁性齒結構，超導超高壓同步調相機拓撲結構如圖1所示。

本文以一臺15 Mvar-35 kV超導超高壓同步調相機為研究對象，基本參數見表1。

1.2 有限元與外電路模型

計算時，先忽略磁場軸向方向的變化，認為電機內的磁場是二維分布，二維平面截面如圖1所示，將三維空間磁場問題簡化為二維問題，則電機瞬態電磁場微分方程^［7］為：

式中：A_z為軸向方向上的磁矢位分量；x、y分別為電機二維平面的橫坐標和縱坐標；J_z為軸向方向上的電流密度；ν為材料的磁阻率；σ為材料的電導率；Γ₁、Γ₂分別為定子外圓和轉子內圓。

應用有限元法數值分析時，需要根據變分原理將要求解的位場問題轉化為條件泛函的極值問題，因此本文將式（1）磁矢位的偏微分方程邊值問題轉換為條件泛函的極值問題，并應用加權余量法得出式（1）的加權積分方程可寫為

式中：{N}^T為T_node維向量函數；T_node為剖分后的有限元模型的總節點數。

對式（2）離散化可得

－Q·pA_z－K·A_z+C·I_b=0。（3）

式中：A_z為T_node維列向量；Q和K為與節點坐標相關系數矩陣；p為微分算子；I_b為線圈電流矩陣，包括定子線圈、勵磁線圈；C為線圈電流與各單元節點間的關聯矩陣。

因超導超高壓調相機定子繞組采用交聯聚乙烯電纜，其電壓等級可大幅度提高，可實現調相機與電網的直連。本文建立的超導超高壓調相機并網運行的場路耦合模型如圖2所示。圖中R_s和L_s分別為定子繞組端部電阻和漏電感，R_f和L_f分別為勵磁繞組端部電阻和漏電感，i_A、i_B、i_C為調相機三相電流，u_SA、u_SB、u_SC為3個電壓源用來模擬無窮大電網。

由圖2列寫定子支路電壓方程為

U=pΨ+RI。（4）

式中：U為電網電壓列向量，U=［u_SA u_SB u_SC］^T；I為電流列向量，I=［i_A i_B i_C］^T；R是電阻矩陣，包括直線段和端部電阻；Ψ是定轉子回路磁鏈。轉子側電壓方程與同步發電機相同，這里不做展開，參考文獻［17］。

對于場路耦合模型，磁鏈Ψ由直線段磁鏈Ψ_L和端部漏磁鏈Ψ_E組成，即

Ψ=Ψ_L+Ψ_E。（5）

線圈直線段磁鏈Ψ_L可由電磁場有限元方程計算得到

Ψ_L=G^T·l_ef·C^T·A_z。（6）

式中：G為所有線圈與回路關聯矩陣；l_ef為電機軸向有效長度。

端部漏磁鏈Ψ_E可寫成

Ψ_E=M_E·I。（7）

式中M_E為端部漏電感，計算方法參考文獻［18］。

將式（5）～式（7）代入到式（4），整理后可得

U=G^T·l_ef·C^T·pA_z+M_E·pI+RI。（8）

1.3 場路耦合模型

線圈電流矩陣I_b與回路電流矩陣I的關系為

I_b=G·I。（9）

將式（9）代入到式（3），并令關聯矩陣N=G·C，將式（3）和式（8）聯立，得到場路耦合數學模型為

－Ql_efN^TM_E·pA_zI+－KNR·A_zI=0U。（10）

1.4 電磁力計算模型

在超導超高壓調相機空載運行時，磁力線的分布如圖3所示。由于采用非磁性定子齒結構，齒部磁阻增大，部分磁力線穿過定子槽，槽漏磁增大，齒壁兩側磁場不對稱，導致齒壁兩側電磁力不均勻，同時槽漏磁使調相機調相運行時繞組產生洛倫茲力。結合非磁性定子齒“細長型”的結構特點，對其所受電磁力及強度進行計算分析。

調相機運行過程中，定子齒部會受到2種電磁力：一種是非磁性齒與氣隙分界面由于磁導率不同而產生的電磁力；另一種是電纜繞組在磁場作用下產生的洛倫茲力。本文要檢驗非磁性齒的結構強度，就要對2種電磁力同時進行計算，來得到齒部受到瞬時電磁力的最大值。

根據麥克斯韋應力法作用于定子齒表面的磁應力公式^［19］為：

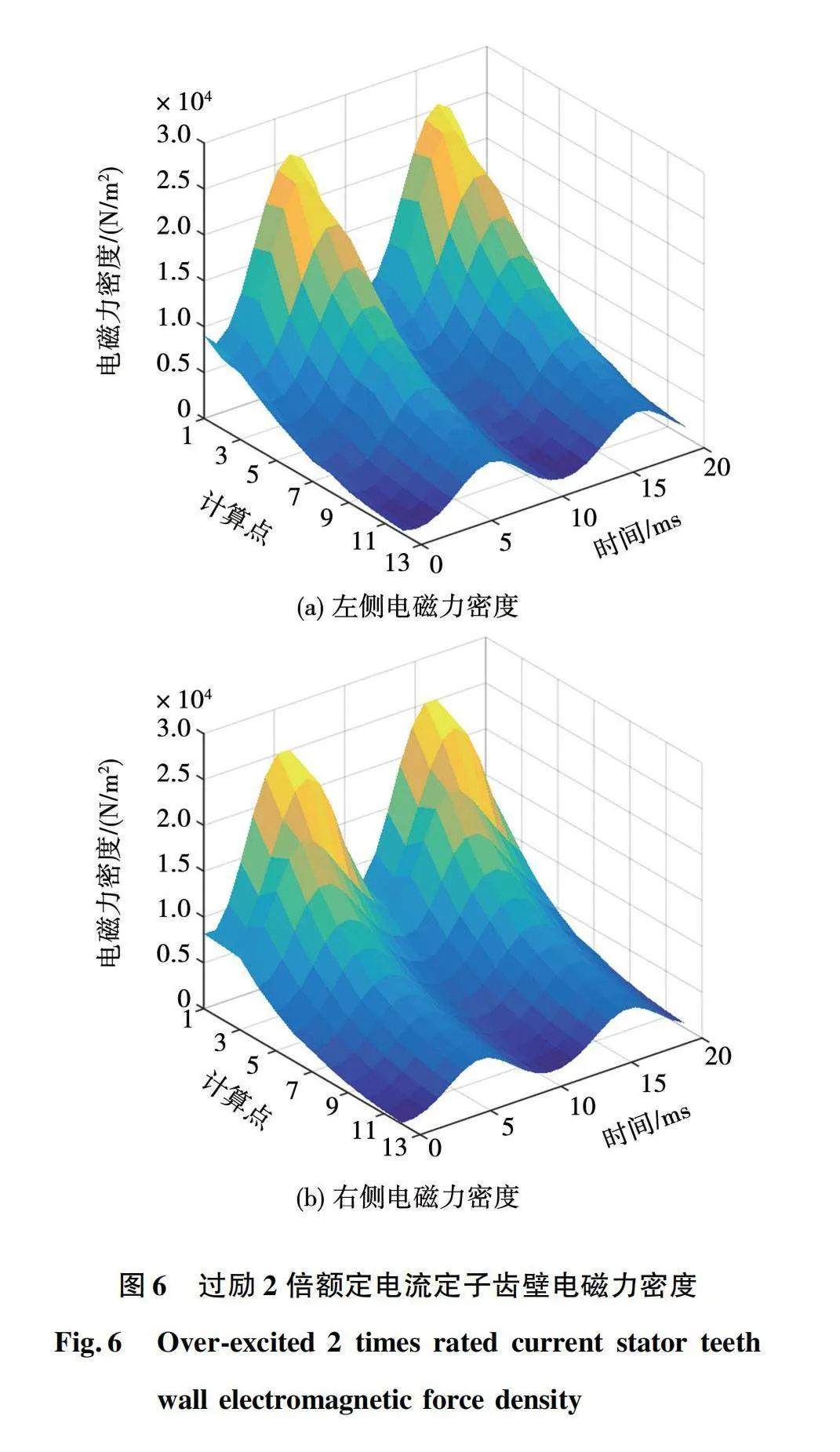
f_n=μ₁－μ₀2μ₁μ₀（B²_n+μ₁μ₀H²_t）；f_t=0。（11）

式中：f_n和f_t分別是定子齒磁應力的法向分量和切向分量；μ₁和μ₀分別是定子齒和空氣的磁導率；B_n和H_t分別是定子齒與空氣交界面上磁感應強度的法向分量和磁場強度的切向分量。

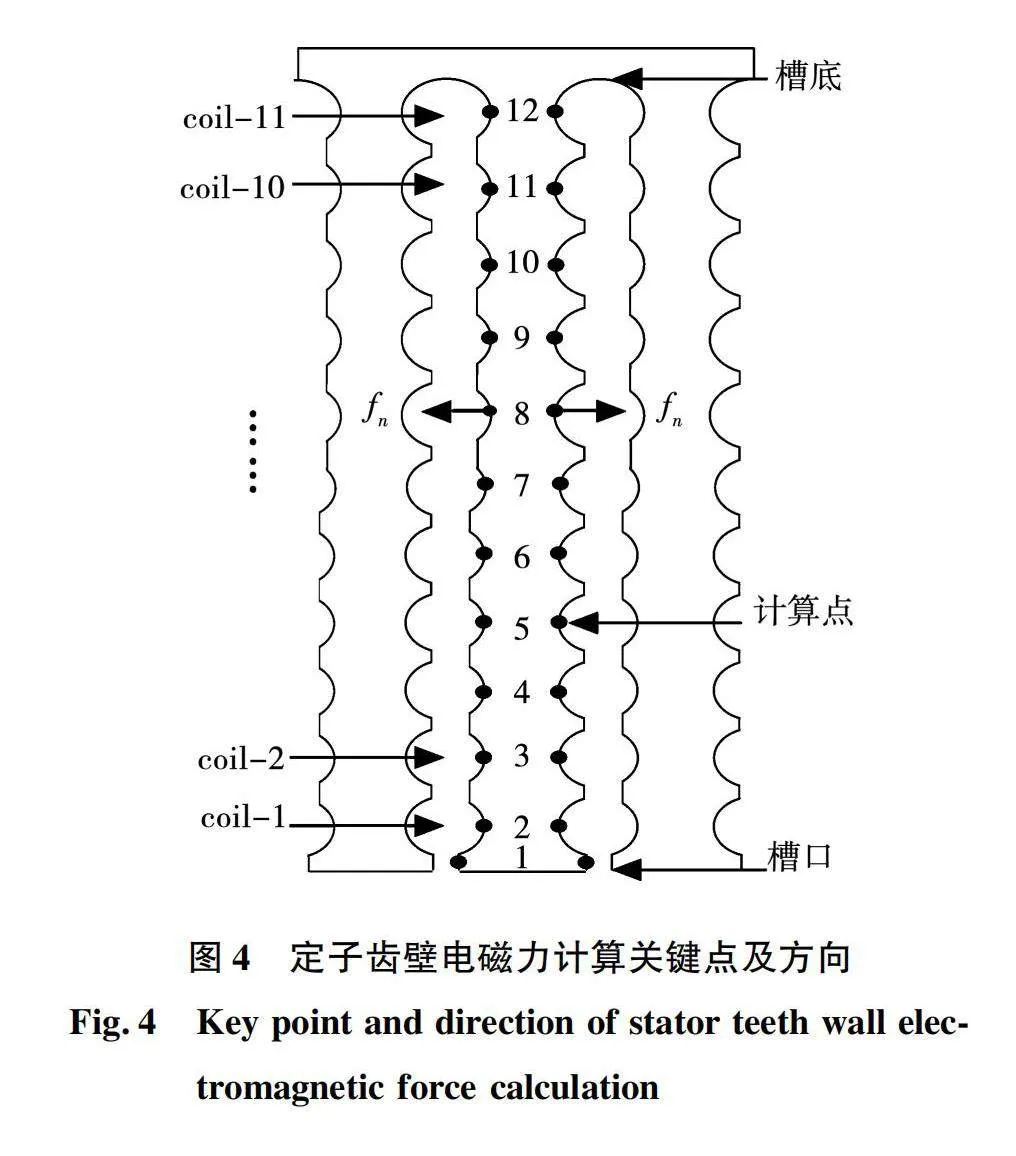
在計算定子齒壁所受電磁力時，在齒壁兩側分別選取了12個關鍵點，如圖4所示。從槽口到槽底，槽內繞組依次命名為coil-1、coil-2、…、coil-10、coil-11，同時電磁力的方向由相對磁導率大的材料指向相對磁導率小的材料，本文定子齒所用材料的相對磁導率為1.05，所以電磁力方向由齒壁指向氣隙。

定子繞組產生的洛倫茲力計算公式^［19］為：

f_it=∫（J_i×B_ir）ldS_i；

f_ir=∫（J_i×B_it）ldS_i；F_t=∑ni=1f_it；

F_r=∑ni=1f_ir。（12）

式中：f_it和f_ir分別是第i個剖分單元的切向和徑向洛倫茲力；J_i為第i個剖分單元的電流密度；B_it和B_ir分別是第i個剖分單元的切向和徑向磁感應強度；l為繞組直線段長度；S_i為第i個剖分單元的面積；F_t和F_r分別是繞組總的切向和徑向洛倫茲力；n為剖分單元總數。

1.5 積分路徑的選取

文獻［9］指出，在應用麥克斯韋應力法時，要關注積分路徑的選取，同時要保證計算精度。在本文計算定子齒壁關鍵點處電磁力時，參考文獻［20］取二階三角形單元中間節點的連線作為積分路徑，并在每個單元的積分路徑上均勻的取6個采樣點，提取每個采樣點的磁場數據，以其算術平均值作為該關鍵點的磁場數據。

2 定子齒電磁力及繞組洛倫茲力計算

2.1 定子齒壁電磁力計算及變化規律

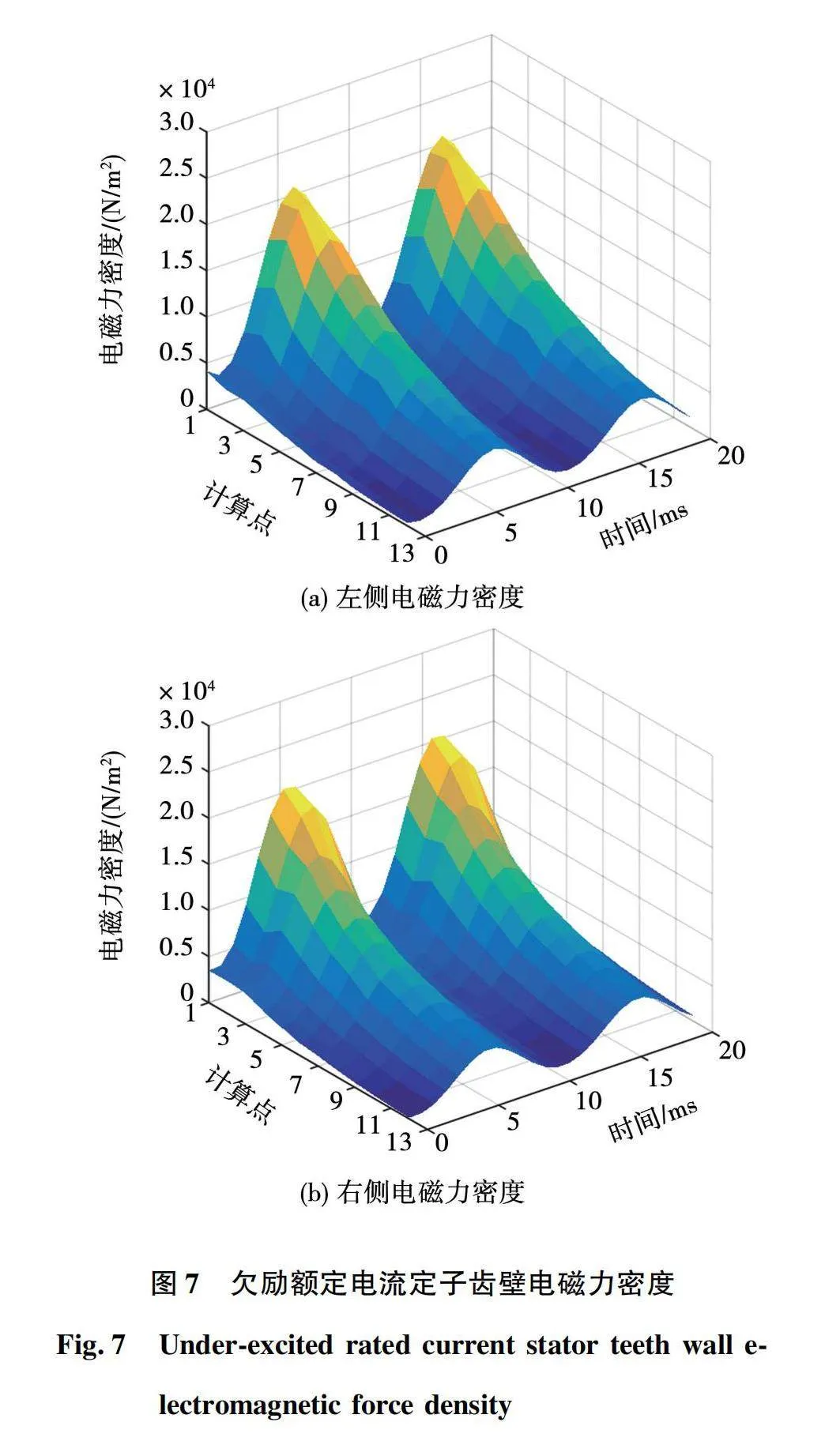
超導超高壓調相機因勵磁能力強、磁負荷高及采用非磁性齒結構電抗參數小等特點，其深度進相和遲相運行能力優于常規調相機^［21］。同時，新型電力系統對調相機的暫態無功支撐能力要求越來越高，短時最大無功功率需達到額定容量的2倍左右^［4］，因此，本文對超導超高壓調相機過勵額定電流、過勵2倍額定電流、欠勵額定電流及欠勵1.5倍額定電流4種運行工況進行仿真計算，得到定子齒壁上的電磁力隨時間及空間的變化規律如圖5、圖6、圖7和圖8所示。

以圖5為例，由于超導超高壓調相機運行狀態的特殊性，在同種工況下定子齒壁兩側受到的電磁力密度相差不大，并且隨著計算點從槽口不斷靠近槽底，定子齒壁所受電磁力密度逐漸減小。左側計算點1處電磁力密度最大值為2.496×10⁴ N/m²，計算點12處的電磁力密度最大值為0.468×10⁴ N/m²；右側計算點1處電磁力密度最大值為2.442×10⁴ N/m²，計算點12處的電磁力密度最大值為0.412×10⁴ N/m²。

在不同工況下，過勵運行時過勵程度越深，定子齒壁所受電磁力密度越大。以左側1計算點為例，過勵額定電流運行時所受最大電磁力密度為2.496×10⁴ N/m²，過勵兩倍額定電流運行時所受最大電磁力密度為2.560×10⁴ N/m²，增大了2.56%。欠勵運行時欠勵程度越深，定子齒壁受到電磁力密度越小。以左側1計算點為例，欠勵額定電流運行時所受最大電磁力密度為2.089×10⁴ N/m²，欠勵1.5倍額定電流運行時所受最大電磁力密度為2.007×10⁴ N/m²，減小了3.93%。

同時每個計算點所受電磁力密度隨時間呈周期性變化，以過勵額定電流運行工況下左側計算點1為例，在0.8和10.8 ms時所受電磁力密度最小為0.695×10⁴ N/m²，在6.4和16.4 ms時所受電磁密度最大為2.496×10⁴ N/m²，大小相差了3.59倍。與過勵運行相比，超導超高壓調相機欠勵運行時，由于勵磁電流的減少磁場減弱，同一時刻相同計算點受到的電磁力密度也比過勵運行時受到的電磁力密度小。

2.2 繞組洛倫茲力計算

根據式（12）計算繞組產生的洛倫茲力。調相機順時針旋轉，洛倫茲力以與旋轉方向一致為正。以coil-1為例，4種工況下繞組產生的切向洛倫茲力大小如圖9所示。同一工況下洛倫茲力隨時間呈周期變化，不同工況下由于調相機過勵運行與欠勵運行時電流相位相差180°，因此繞組產生的洛倫茲力相位同樣相差180°，過勵運行時多數時刻洛倫茲力與調相機旋轉方向相反，欠勵運行時多數時刻洛倫茲力與調相機旋轉方向相同。并且隨著調相深度的增加，繞組受到的洛倫茲力也相應增大，過勵2倍額定電流運行時繞組所受最大洛倫茲力為-695 N（此時洛倫茲力方向與調相機旋轉方向相反，下同），過勵額定電流運行時繞組所受最大洛倫茲力為-533 N，欠勵1.5倍額定電流運行時繞組所受最大洛倫茲力為500 N，欠勵額定電流運行時繞組所受最大洛倫茲力為314 N。

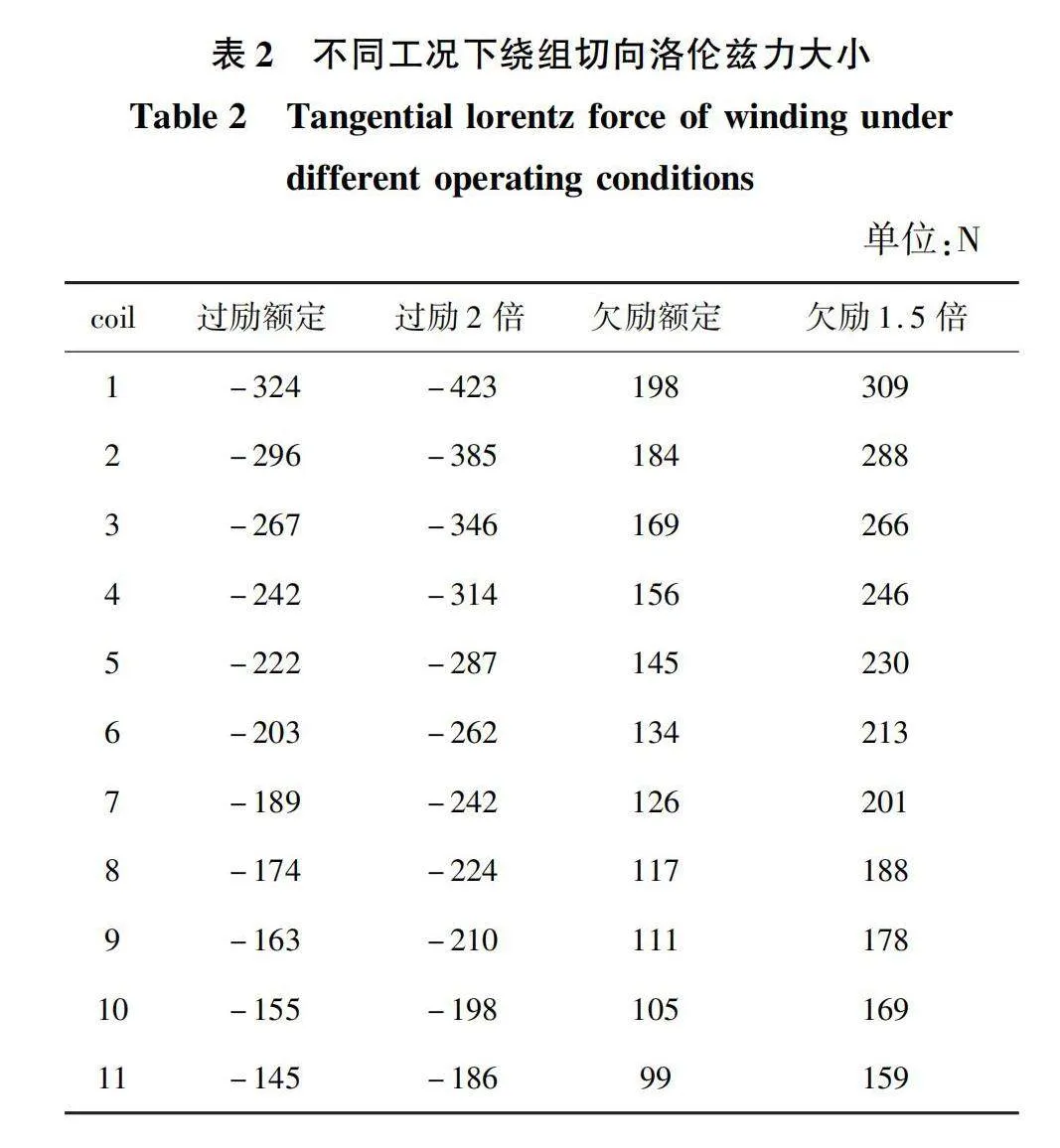
根據2.1節，取一個周期內齒壁電磁力密度最大的時刻為研究時間節點，此時，4種工況下同一個槽內11個電纜繞組的洛倫茲力如表2所示。過勵運行時，在齒壁電磁力密度最大時刻，繞組產生的切向洛倫茲力方向向左，此時只有右側齒壁受到洛倫茲力的作用；而欠勵運行時，繞組產生的切向洛倫茲力方向向右，此時只有左側齒壁受到洛倫茲力的作用。

2.3 定子齒壁總的受力計算

將定子齒壁兩側最大電磁力密度進行積分，可得到每個槽壁面受到的實際電磁力大小。同時計算同一時刻定子繞組產生的切向洛倫茲力，進行疊加得到齒壁兩側受到總的電磁力。

以過勵額定電流運行為例，在定子齒壁電磁力密度最大的時刻，只有右側齒壁受到了洛倫茲力的作用，齒壁受到的總電磁力如圖10所示。由于計算點1在槽口位置，側面積比槽內齒壁小，所以槽口實際的電磁力比槽內小，因此圖10中的波形從計算點1到計算點2有一個突增，同時槽口不受洛倫茲力影響其電磁力大小不變，所以右側電磁力和右側電磁力＋洛倫茲力2個波形起點相同。

過勵工況下定子齒兩側總的受力如圖11所示，結合表2可知，在過勵運行電磁力密度最大的時刻，繞組產生向左的洛倫茲力，所以右側齒壁比左側齒壁受到的力相對較小。以過勵額定電流運行時計算點2為例，左側受力372.49 N，右側受力157.5 N。同時過勵2倍額定電流運行時繞組產生的洛倫茲力比過勵額定電流運行時大，因此其右側齒壁受到的力要比過勵額定電流運行時右側齒壁受到的力小。以計算點2為例，過勵額定電流運行時右側受力157.5 N，過勵2倍額定電流運行時右側受力67.68 N。

欠勵工況下定子齒兩側總的受力如圖12所示，結合表2可知，在欠勵運行電磁力密度最大的時刻，繞組產生向右的洛倫茲力，所以左側齒壁比右側齒壁受到的力相對較小。以欠勵額定電流運行時計算點2為例，左側受力122.58 N，右側受力408.2 N。同時欠勵1.5倍額定電流運行時繞組產生的洛倫茲力比欠勵額定電流運行時大。因此其左側齒壁受到的力比欠勵額定電流運行時左側齒壁受到的力小。以計算點2為例，欠勵額定電流運行時左側受力122.58 N，欠勵1.5倍額定電流運行時左側受力1.47 N。

由圖10～圖12可知，在計及繞組產生的洛倫茲力之后，定子齒壁兩側的受力相差較大。同種工況下，調相運行程度越深兩側受力相差越大。因此需要對定子齒的強度進行分析，以確保電機可以安全運行。

3 定子非磁性齒強度計算

3.1 定子齒模型與載荷施加

在workbench中建立了定子齒的三維模型，為保證計算精度采用四面體網格進行劃分，單元尺寸為10 mm，模型共有5 907 646個節點和1 191 216個單元，如圖13所示。

將2.3節計算結果中定子齒壁兩側受力作為載荷，施加到定子齒壁上。以過勵額定電流運行工況為例，施加到定子齒壁上的載荷如圖14所示，圖中箭頭方向為載荷方向，即定子齒壁受力方向。

3.2 強度計算方法

本文超導超高壓同步調相機的定子齒所用材料為316L不銹鋼（許用應力為290 MPa），對其進行強度計算采用第四強度理論及Von Mises等效應力，計算公式^［22］為

σ_r4=

12［（σ₁－σ₂）²+（σ₂－σ₃）²+（σ₃－σ₁）²］。（13）

式中：σ_r4為等效應力；σ_i為3個方向上的主應力。

通過等效應力對結構進行強度評估時，還要引入安全系數S，即

S=σ_pσ_d。（14）

式中：σ_p為材料許用應力；σ_d為計算應力。

根據安全系數S的定義，在調相機運行過程中，非磁性齒內部產生的等效應力應當小于所用材料的許用應力，才能保證非磁性齒不會發生彎曲斷裂，以滿足強度的要求（即安全系數S大于1，數值越大說明材料的強度越大，能更好滿足非磁性定子齒對強度的要求）。

3.3 強度計算結果及分析

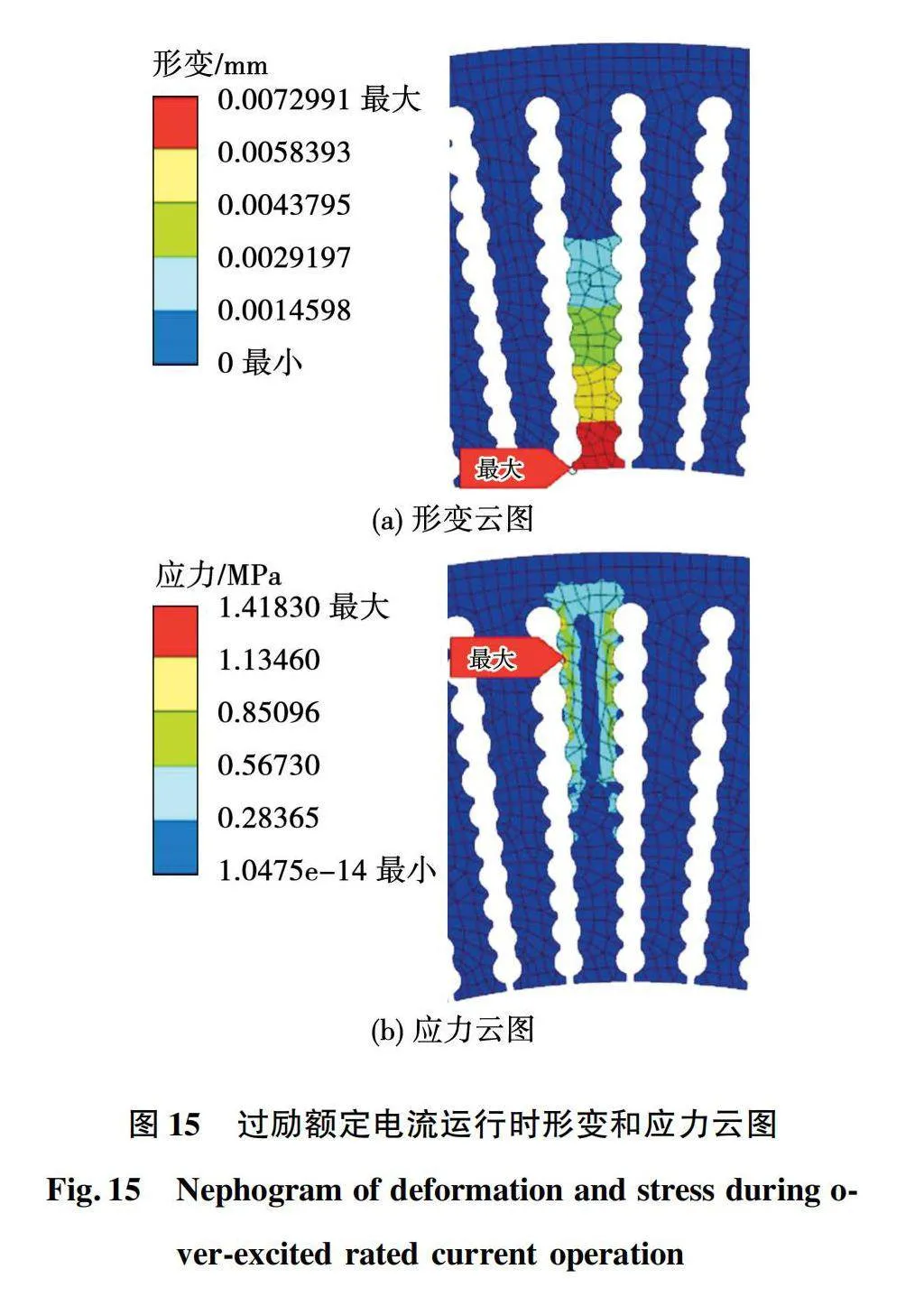
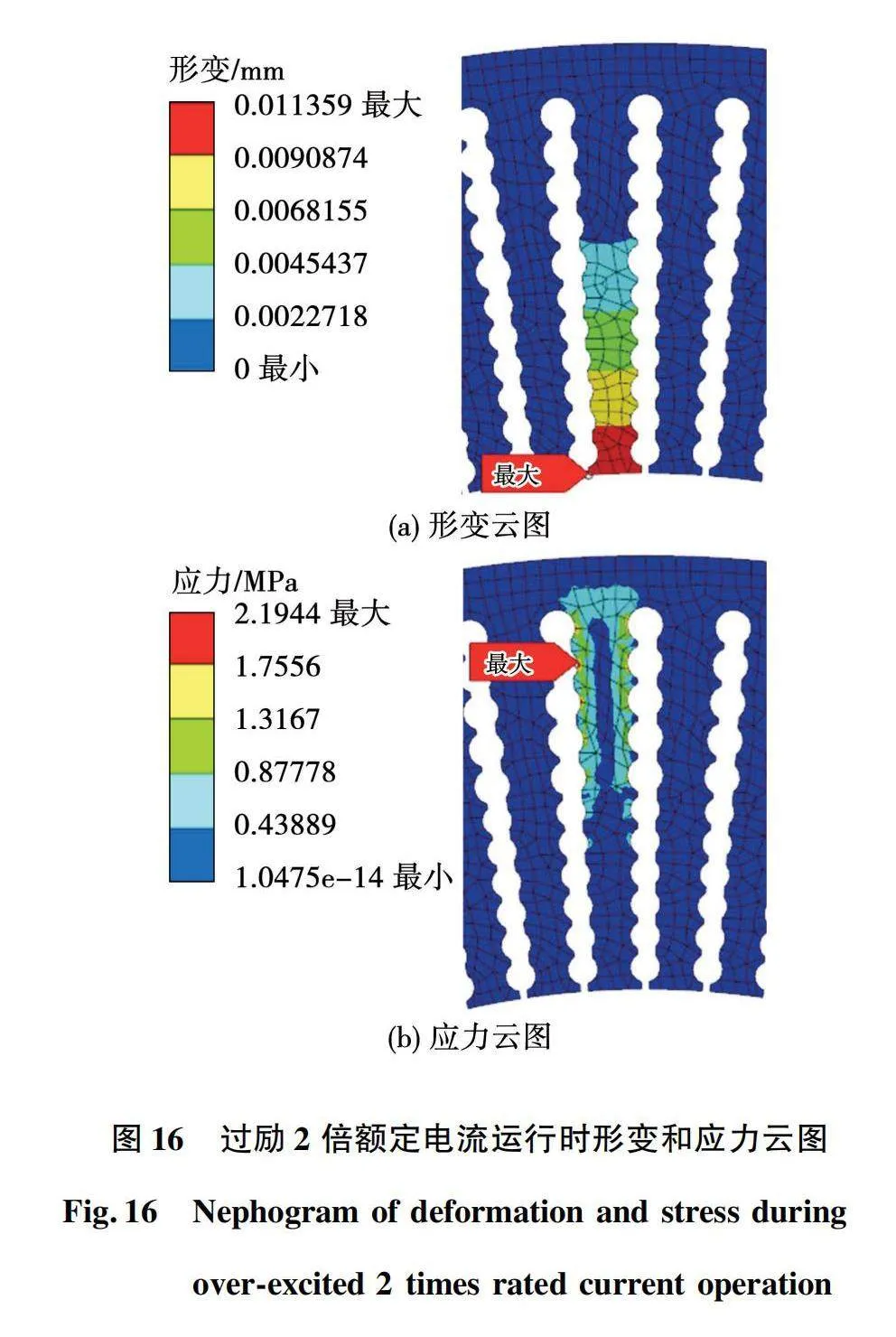
不同工況下定子齒部的形變和應力云圖如圖15～圖18所示，同時受到的最大應力和形變量如表3所示。

過勵額定電流運行時形變最大為0.730×10^-2 mm，從圖15（a）可以看出，此時形變最大位置在槽口處，但形變量遠小于槽口寬度5 mm。此時最大應力為1.418 MPa，從圖15（b）中看到，應力最大位置在計算點11所處的齒壁上，根據式（14），得到此時的安全系數為204.47遠大于1，說明選用的非磁性齒材料的機械強度能夠滿足運行需要。

過勵2倍額定電流運行時，由表2可得，由于勵磁電流和負載電流的增大，導致定子齒受到電磁力增大，齒壁的形變和應力也相應增大。形變最大為1.136×10^-2 mm，比過勵額定電流運行時增大了55.62%，仍遠小于槽口寬度5 mm；最大應力為2.194 MPa，比過勵額定電流運行時增大了54.72%，安全系數為132.15遠大于1，能滿足運行需要。

與過勵額定電流運行相比，欠勵額定電流運行時定子齒的形變和應力都有所減小，但變化不大。欠勵1.5倍額定電流運行與過勵2倍額定電流運行時的形變和應力接近。因此，非磁性齒的強度能滿足調相機在不同工況下的運行要求。

4 結 論

本文建立了超導超高壓同步調相機并網運行的場路耦合仿真模型，結合麥克斯韋應力法和洛倫茲力原理對定子齒壁受到的總電磁力進行計算。將計算得到的電磁力作為載荷，分析了多工況下非磁性定子齒的應力分布和形變規律，得到以下結論：

1）同種運行工況下，定子齒壁兩側所受電磁力相差不大，同時越靠近槽底電磁力越小；不同工況下，隨著勵磁電流的增大，定子齒壁電磁力也隨之增大。

2）將定子齒壁電磁力與繞組產生的切向洛倫茲力疊加后，定子齒壁兩側電磁力發生變化，齒壁兩側受力相差較大。以過勵2倍額定電流運行工況為例，齒壁兩側電磁力最大差值為354 N，最小差值為162 N，這是導致定子齒壁產生形變的主要原因。

3）在調相機運行過程中，定子齒槽口位置形變最嚴重，且沿徑向向槽底方向形變量逐漸減小。以本文形變最嚴重的過勵2倍額定電流運行工況為例，槽口最大形變為1.136×10^-2 mm，其形變量遠小于槽口寬度5 mm，能滿足運行要求。

4）在調相機運行過程中，定子齒所受應力主要集中在槽底，但即使在應力最大部位，其安全系數遠大于1，因此調相機正常運行時非磁性定子齒不會發生疲勞斷裂。

參 考 文 獻：

［1］TELEKE S， ABDULAHOVIC T， THIRINGER T， et al. Dynamic performance comparison of synchronous condenser and SVC［J］. IEEE Transactions on Power Delivery， 2008， 23（3）： 1606.

［2］戈寶軍， 王曉文， 陶大軍， 等. 能量變換器樣機的研制［J］. 電機與控制學報， 2008， 12（4）： 370.

GE Baojun， WANG Xiaowen， TAO Dajun， et al. Development of powerformer prototype［J］. Electric Machines and Control， 2008， 12（4）; 370.

［3］戈寶軍， 張大魁， 梁艷萍. 能量變換器及其最新發展［J］. 電工技術學報， 2005， 20（1）： 26.

GE Baojun， ZHANG Dakui， LIANG Yanping. Powerformer and its recent development［J］. Transactions of China Electrotechnical Society， 2005， 20（1）： 26.

［4］李桂芬， 李小龍， 孫玉田. 300 Mvar空冷隱極同步調相機暫態特性仿真分析［J］. 大電機技術， 2021（5）： 33.

LI Guifen， LI Xiaolong， SUN Yutian. Simulation and analysis of transient characteristics of 300 Mvar air-cooled cylindrical rotor synchronous condenser［J］. Large Electric Machine and Hydraulic Turbine， 2021（5）： 33.

［5］REN Z. Comparison of different force calculation met-hods in 3D finite element modelling［J］. IEEE Transactions on Magnetics， 1994， 30（5）： 3471.

［6］戴魏， 余海濤， 胡敏強. 基于虛功法的直線同步電機電磁力計算［J］. 中國電機工程學報， 2006， 26（22）： 110.

DAI Wei， YU Haitao， HU Minqiang. Electromagnetic force computation of linear synchronous motor with virtual work method［J］. Proceedings of the CSEE， 2006， 26（22）： 110.

［7］肖士勇， 戈寶軍， 陶大軍， 等. 同步發電機定子繞組匝間短路時轉子動態電磁力計算［J］. 電工技術學報， 2018， 33（13）： 2956.

XIAO Shiyong， GE Baojun， TAO Dajun， et al. Calculation of rotor dynamic electromagnetic force of synchronous generator under the stator winding interturn short circuit fault［J］. Transactions of China Electrotechnical Society， 2018， 33（13）： 2956.

［8］肖士勇， 王云陽， 戈寶軍. 中性點側小匝數相間短路下水輪發電機鐵心動態電磁力［J］. 哈爾濱理工大學學報， 2021， 26（6）： 73.

XIAO Shiyong， WANG Yunyang， GE Baojun. Dynamic electromagnetic force of stator core for hydro-generators under phase to phase short circuit with two fault points close to the neutral point［J］. Journal of Harbin University of Science and Technology， 2021， 26（6）： 73.

［9］戈寶軍， 姜超， 呂品， 等. 大型核電汽輪發電機非全相運行轉子動態電磁力分析［J］. 電機與控制學報， 2021， 25（5）： 26.

GE Baojun， JIANG Chao， Lü Pin， et al. Analysis of rotor dynamic electromagnetic force in large nuclear turbines under open-phase operation condition［J］. Electric Machines and Control， 2021， 25（5）： 26.

［10］萬書亭， 彭勃， 何玉靈. 支路不對稱發電機故障下定子電磁力仿真分析［J］. 電機與控制學報， 2018， 22（9）： 33.

WAN Shuting， PENG Bo， HE Yuling. Analysis and simulation of stator electromagnetic pull under internal faults of asymmetric-branch generator［J］. Electric Machines and Control， 2018， 22（9）： 33.

［11］CAO Yongjuan， YU Liling， JIA Hongyun. Rotor mechanical stress and deformation analysis of coreless stator axial-flux permanent magnet machines［C］//2015 IEEE International Magnetics Conference， May 11-15， 2015， Beijing， China. 2015： 1.

［12］何海翔， 陳志輝， 梅慶梟， 等. 聚磁型無源轉子橫向磁通永磁電機電磁力及轉子機械強度的分析［J］. 電工技術學報， 2017， 32（15）： 10.

HE Haixiang， CHEN Zhihui， MEI Qingxiao， et al. Analysis of electromagnetic force and rotor mechanical strength on flux-concentrating transverse flux PM machine with passive rotor［J］.Transactions of China Electrotechnical Society，2017，32（15）：10.

［13］謝穎， 馮春爽， 楊忠學， 等. 籠型感應電動機斷條故障前后轉子電磁力計算及結構靜力學分析［J］. 電工技術學報， 2015， 30（15）： 164.

XIE Ying， FENG Chunshuang， YANG Zhongxue， et al. Electromagnetic force calculation and structural static analysis on the rotor of squirrel-cage induction motors before and after the broken bars fault［J］. Transactions of China Electrotechnical Society， 2015， 30（15）： 164.

［14］STANCHEVA R D， IATCHEVA I I. 3-D electromagnetic force distribution in the end region of turbogenerator［J］. IEEE Transactions on Magnetics， 2009， 45（3）： 1000.

［15］趙洋， 嚴波， 曾沖， 等. 大型汽輪發電機定子端部電磁力作用動態響應分析［J］. 電工技術學報， 2016， 31（5）： 199.

ZHAO Yang， YAN Bo， ZENG Chong， et al. Dynamic response analysis of large turbogenerator stator end structure under electromagnetic forces［J］. Transactions of China Electrotechnical Society， 2016， 31（5）： 199.

［16］史正軍， 宋萌， 譚軍， 等. 超導同步調相機低溫系統設計與試驗研究［J］. 低溫物理學報， 2021， 43（6）： 319.

SHI Zhengjun， SONG Meng， TAN Jun， et al. Design and experimental study on cryogenic system of superconducting synchronous condenser［J］. Low Temperature Physical Letters， 2021， 43（6）： 319.

［17］孫宇光， 王祥珩， 桂林， 等. 場路耦合法計算同步發電機定子繞組內部故障的暫態過程［J］. 中國電機工程學報， 2004， 24（1）： 136.

SUN Yuguang， WANG Xiangheng， GUI Lin， et al. Transient calculation of stator’s internal faults in synchronous generator using fem coupled with multi-loop method［J］. Proceedings of the CSEE， 2004， 24（1）： 136.

［18］陳世坤. 電機設計（第二版）［M］. 北京：機械工業出版社， 2000：50-61.

［19］湯蘊璆. 電機內的電磁場（第二版）［M］. 北京：科學出版社， 1998： 255-265.

［20］閻秀恪， 謝德馨， 高彰燮， 等. 電磁力有限元分析中麥克斯韋應力法的積分路徑選取的研究［J］. 電工技術學報， 2003， 18（5）： 32.

YAN Xiuke， XIE Dexin， GAO Zhangxie， et al. Research on integration path selection of Maxwell stress tensor method used in electromagnetic force FEM analysis［J］. Transactions of China Electrotechnical Society， 2003， 18（5）： 32.

［21］史正軍， 宋彭， 宋萌， 等. 10 Mvar超導同步調相機總體電磁設計［J］. 南方電網技術， 2021， 15（1）： 76.

SHI Zhengjun， SONG Peng， SONG Meng， et al. Electromagnetic design of a 10 Mvar superconducting dynamic synchronous condenser［J］. Southern Power System Technology， 2021， 15（1）： 76.

［22］王旭燦， 王劍， 王子明. 某軸懸式牽引電機疲勞強度分析及優化［J］. 機械制造與自動化， 2023， 52（3）： 176.

WANG Xucan， WANG Jian， WANG Ziming. Analysis and optimation of fatigue strength of an axle-mounted traction motor［J］. Machine Building amp; Automation， 2023， 52（3）： 176.

（編輯：劉琳琳）