基于遺傳算法和Flexsim仿真的裝配線平衡研究

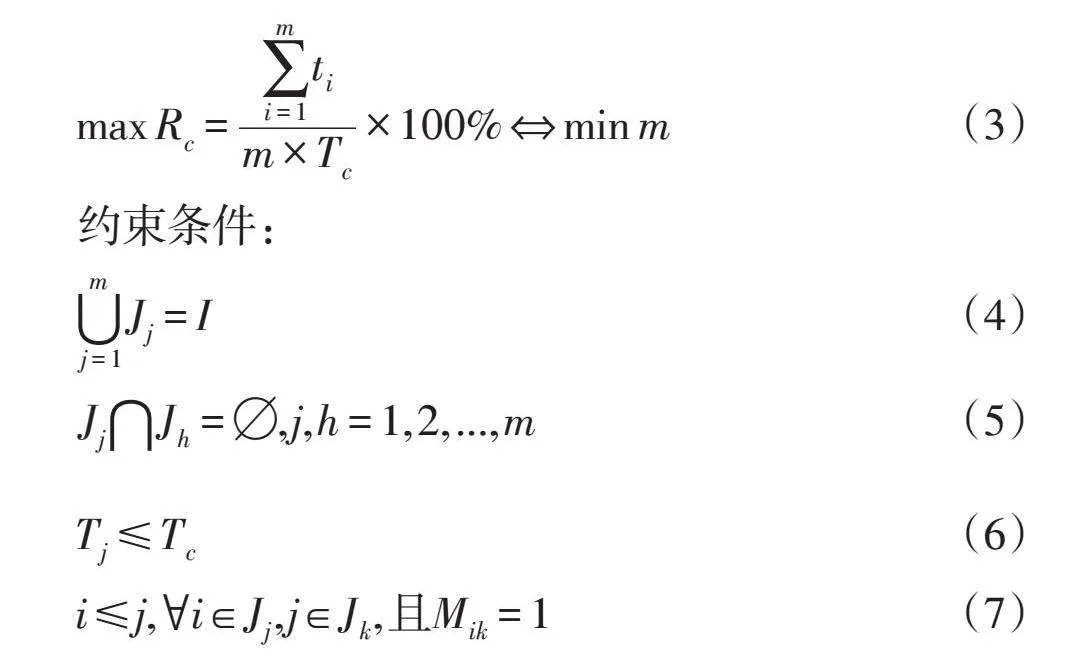
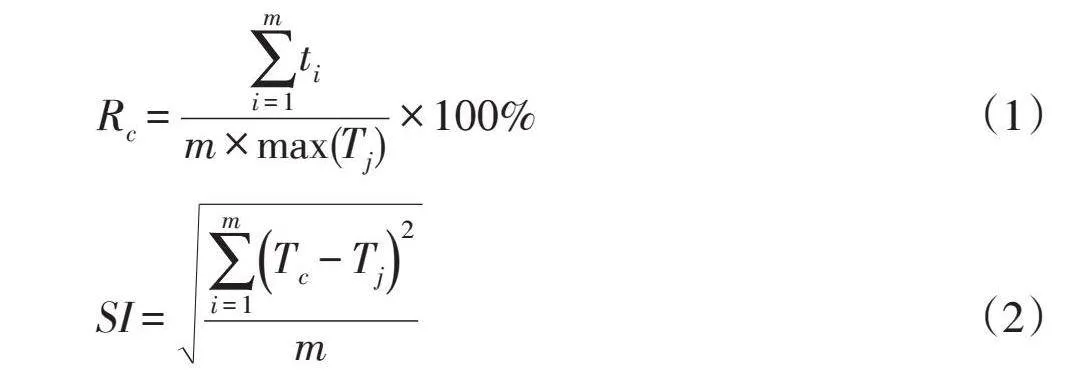
摘要：針對某公司尿素泵流道塊裝配線平衡率低，作業(yè)分配不均衡的問題，建立了以最大平衡率為目標(biāo)的數(shù)學(xué)模型，應(yīng)用遺傳算法對該模型進行優(yōu)化求解，并借助Flexsim仿真軟件驗證該優(yōu)化方案的合理性和可靠性。研究表明，當(dāng)尿素泵流道塊裝配線的節(jié)拍確定時，工位數(shù)最小為5，此時裝配線平衡率最高，平滑性指數(shù)最低，同時軟件仿真結(jié)果顯示裝配線上各工位的利用率均較高，驗證了該裝配線改善方案的可行性。

關(guān)鍵詞：裝配線平衡；遺傳算法；優(yōu)化；Flexsim仿真

中圖分類號：TP391.9；TP305文獻標(biāo)志碼：A文章編號：2095－414X（2024）06－0058－05

0引言

裝配線平衡問題在制造領(lǐng)域一直是一項重要的研究課題[1]。裝配線平衡率越高，各工序浪費的時間就越少，生產(chǎn)效率就越高。在制造業(yè)競爭如此激烈的情況下，各企業(yè)為保持競爭力，通過研究裝配線平衡來合理地利用和分配人力和設(shè)備資源，以實現(xiàn)產(chǎn)量的最大化。

目前國內(nèi)外關(guān)于裝配線平衡問題的學(xué)術(shù)研究有很多，Lee，A.H.I[2]等通過建立模糊多目標(biāo)線性規(guī)劃模型和遺傳算法模型的方法來解決多目標(biāo)的裝配線平衡問題。黃鵬鵬等[3]提出一種雙種群的改進遺傳算法，對血透管裝配線進行分析，以最大平衡率和最小平滑性指數(shù)為目標(biāo)建立數(shù)學(xué)模型。鄧超等[4]提出了一種考慮工人分配的多目標(biāo)鯨魚優(yōu)化算法，以連接器裝配線為例，驗證了算法可同時優(yōu)化生產(chǎn)節(jié)拍、平滑指數(shù)和工人學(xué)習(xí)時間三個目標(biāo)。邱德元[5]等結(jié)合多媒體技術(shù)和工業(yè)工程方法，研究了托輪裝配線的線平衡問題，并從多個維度對所有工序進行了分析和改進。

本文將以某企業(yè)尿素泵流道塊裝配線為研究對象，針對該裝配線平衡率低的問題，搭建以最大平衡率為目標(biāo)函數(shù)的尿素泵流道塊裝配線數(shù)學(xué)模型，并運用遺傳算法對裝配線進行優(yōu)化，得到最小工位數(shù)，再借助Flexsim軟件對裝配線進行建模仿真，驗證方案的可行性，最后對優(yōu)化前后效果對比評價。

1問題描述

作為被廣泛用于中重型柴油車尾氣NOx排放控制的選擇性催化還原系統(tǒng)SCR（Selective Catalytic Reduc?tion）核心部件之一，尿素泵的性能對發(fā)動機的排放功能有至關(guān)重要的作用。目前某企業(yè)由于尿素泵裝配線不平衡問題，導(dǎo)致作業(yè)人員等待浪費時間，產(chǎn)品生產(chǎn)效率不高且質(zhì)量得不到保證。為提高生產(chǎn)效率，滿足市場需求，同時進一步提高裝配線平衡率，本文以尿素泵流道塊裝配線為對象，對該裝配線的平衡問題進行研究。

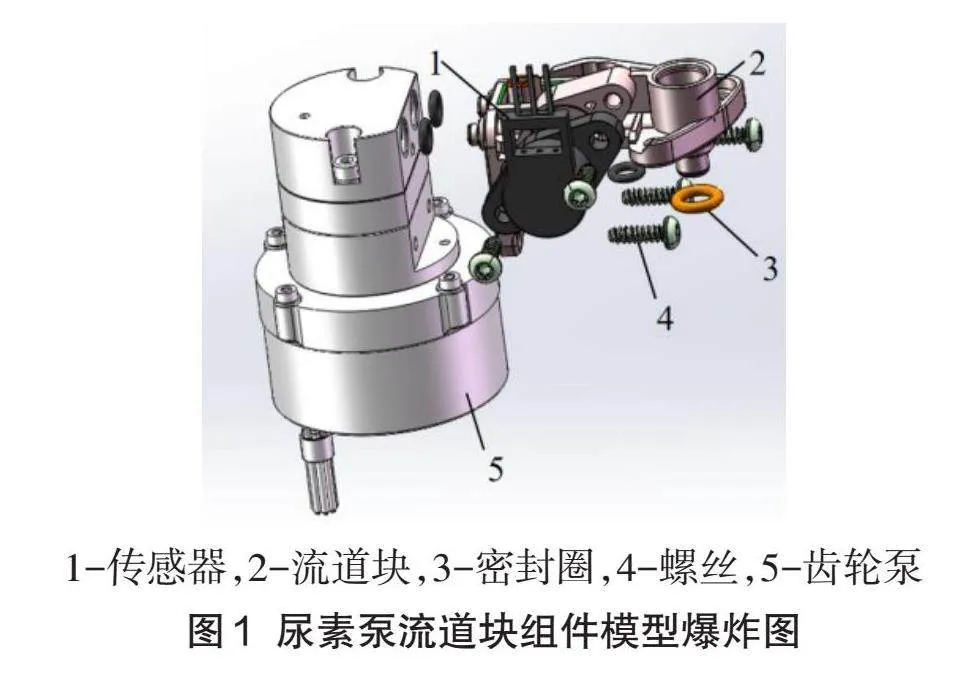
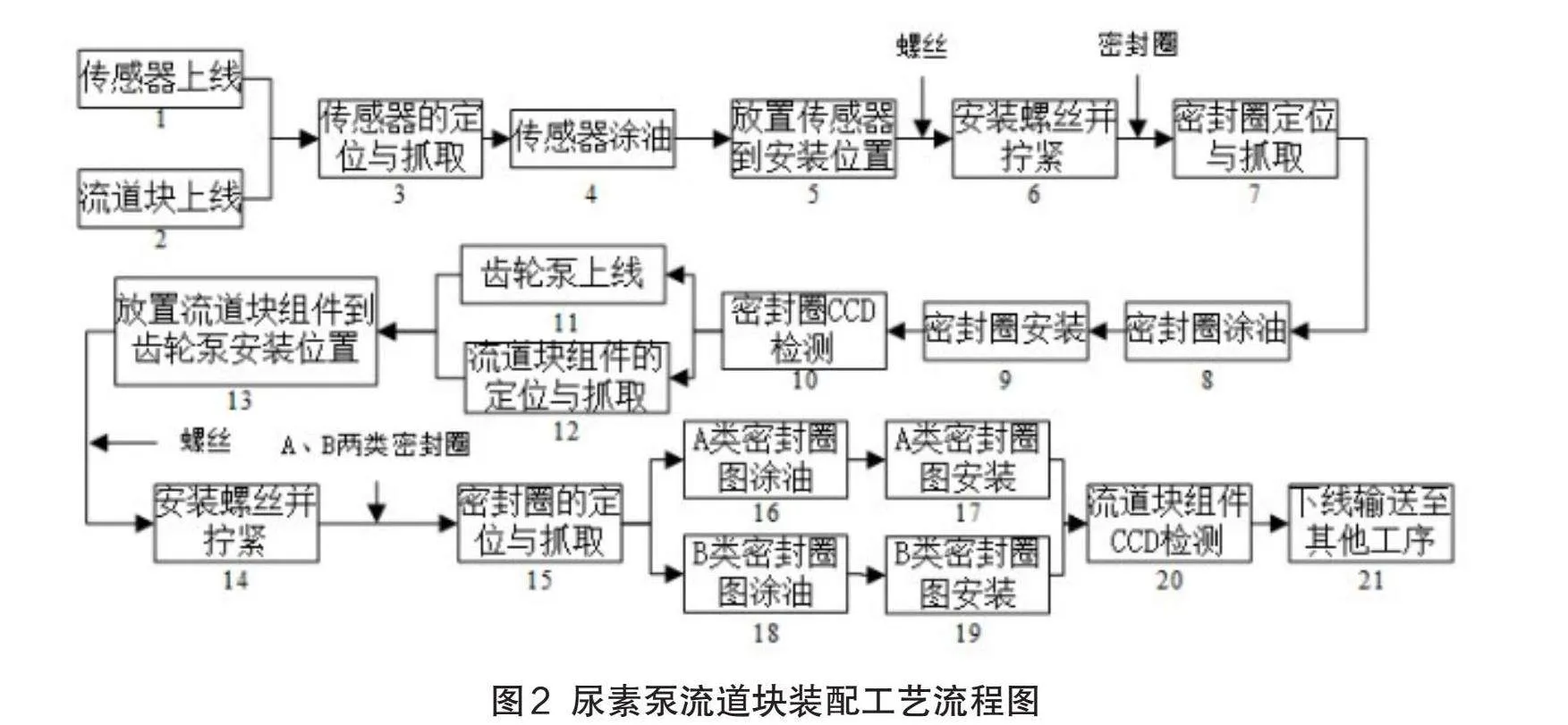
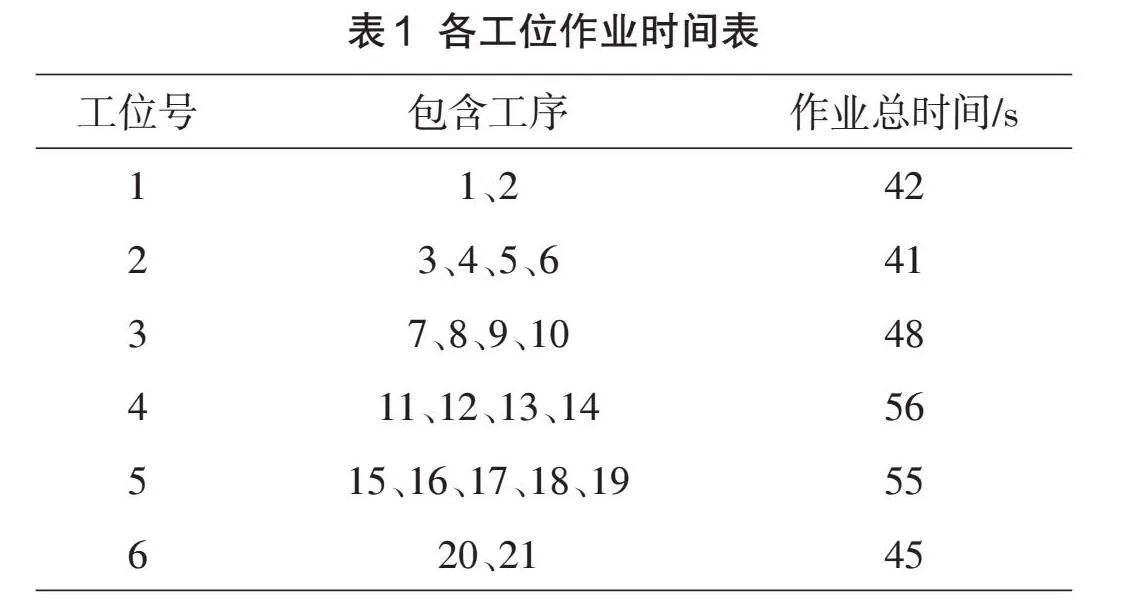
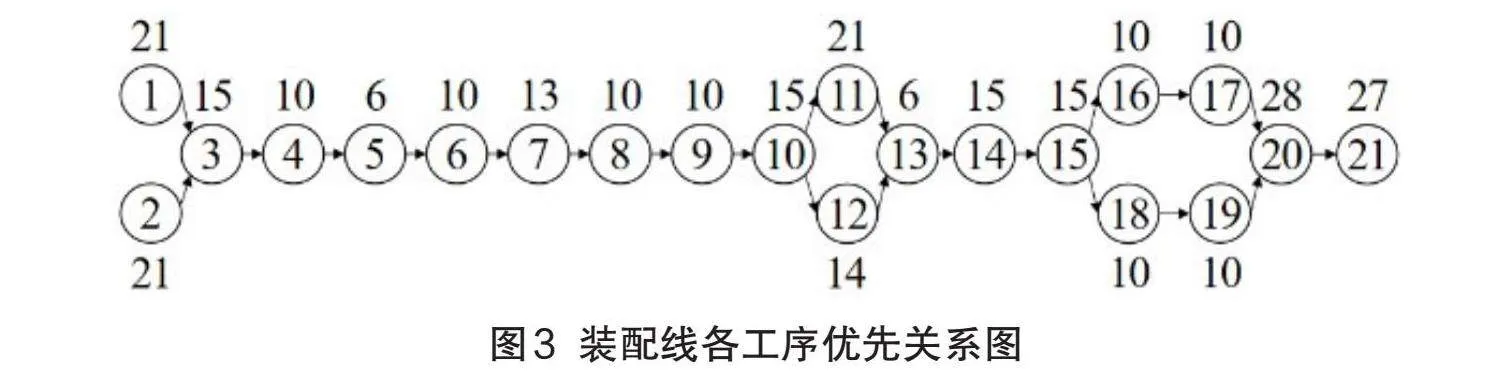
尿素泵流道塊組件模型結(jié)構(gòu)如圖1所示，結(jié)合尿素泵裝配現(xiàn)狀，繪制尿素泵流道塊裝配工藝流程圖，如圖2所示。根據(jù)現(xiàn)場調(diào)研，對裝配線的工位及各工序的工時測定，繪制了各工序作業(yè)時間表，目前該裝配線共分為6個工位，21道工序，如表1所示。考慮到各工序之間的緊前關(guān)系，繪制一種以節(jié)點形式表示的裝配線優(yōu)先關(guān)系圖，如圖3所示。

據(jù)統(tǒng)計尿素泵裝配線的日產(chǎn)量要達到約420件才能滿足需求，每天實際工作時間按7h算，則流道塊組件的生產(chǎn)節(jié)拍為60s。裝配線的平衡效果可由平衡率和平滑性指數(shù)來衡量，平衡率是反映裝配線的平衡狀況和生產(chǎn)效率的重要指標(biāo)；平滑性指數(shù)體現(xiàn)了各工位的負荷程度，數(shù)值越小表明各工位的負荷越均衡，平衡效果越好[6]。計算公式分別為：

Rc=m×x（i）（Tj）×100%（1）

式中，Rc為平衡率，SI是平滑性指數(shù)，ti為工序i所需要的作業(yè)時間，m為工位數(shù)量，Tj為工位j的總時間，Tc為生產(chǎn)節(jié)拍。由上式計算得到目前裝配線平衡率Rc為85.42%，平滑性指數(shù)SI為13.5093，該裝配線還有進一步優(yōu)化的空間。

2基于遺傳算法的模型建立及求解

2.1模型建立

遺傳算法是根據(jù)生物界的自然選擇機制提出來的一種優(yōu)化搜索算法。通過對初始種群不斷進行選擇、交叉和變異等操作，從而產(chǎn)生適應(yīng)度更大的群體，直到找到最優(yōu)的可行解[7-8]。

由裝配線平衡問題的分類可知，本文對尿素泵流道塊裝配線平衡問題的研究屬于第一類裝配線平衡問題，即裝配線的生產(chǎn)節(jié)拍已知，在滿足生產(chǎn)約束的條件下，按照合適的規(guī)則將所有的工序單元分配至各工位，得出最小工位數(shù)，同時使得裝配線平衡率達到最高[9]。因此對該裝配線建立以下數(shù)學(xué)模型：

目標(biāo)函數(shù)：

max Rc=T（t i）c×100%?min m

約束條件：

Jj=I

Jj∩Jh=?，j，h=1，2，...，m

Tj≤Tc

i≤j，?i∈Jj，j∈Jk，且Mik=1

上式中各符號定義：I為裝配線上任務(wù)的集合，I={1，2，...，m}；Jj為分配到第j個工位的任務(wù)集合；M為裝配優(yōu)先關(guān)系矩陣，若工序i是工序k的緊前工序，則Mik=1，否則，Mik=0。

目標(biāo)函數(shù)（3）表示在生產(chǎn)節(jié)拍一定時，按約束條件劃分工位數(shù)，使裝配線平衡率最大，即工位數(shù)最小。約束條件（4）表示所有工位的作業(yè)集合與裝配線上的任務(wù)集合相等。約束條件（5）表示工序分配的限制條件，每道工序都要分配至一個工位，且同一工序不能分配至兩個及以上工位中。約束條件（6）表示每一個工位的總時間要小于或等于生產(chǎn)節(jié)拍。約束條件（7）表示裝配線上各工序的優(yōu)先關(guān)系，確保緊后工序不會被分配在緊前工序前面的工位中。

2.2算法求解

（1）編碼及生成初始種群。本文依據(jù)裝配優(yōu)先關(guān)系圖，將各工序依次排成一列，每道工序?qū)?yīng)染色體上的一個基因位，當(dāng)所有工序都按順序排列完成，就會得到一條經(jīng)過編碼的染色體。

初始種群一般由多條染色體組成，每條染色體都必須滿足優(yōu)先關(guān)系矩陣M的加工順序約束。本研究初始化種群采用優(yōu)先關(guān)系矩陣行列置0的方法，具體步驟：①隨機選取優(yōu)先關(guān)系矩陣中全為0的那一列，對應(yīng)的工序的編號作第1個編碼位。②將已編號序列的那一行置為0，即生成第一個個體。③重復(fù)1、2操作，直到矩陣全部為0。重復(fù)以上步驟可獲得初始個體，并用該方法生成多個初始個體則可以組成一個初始種群。

（2）譯碼。譯碼是在一定的規(guī)則下，將初始種群內(nèi)各個初始個體表示的工序依次分配給各個工位的過程[10]。本文研究的尿素泵流道塊裝配線平衡問題，是在給定生產(chǎn)節(jié)拍的條件下，根據(jù)染色體中的工序順序，將各個工序依次分配給各個工位，使工位數(shù)量最少，平衡率最高。

基于給定節(jié)拍Tc，將盡可能多的n個工序依照編碼順序分配到m個工位中，每個工位的時間分別為T1，T2，T3，...，Tm，均要滿足Tj≤Tc，所有工序分配完成即可求得工位數(shù)工序的劃分結(jié)果。

（3）適應(yīng)度評估。適應(yīng)度表示個體對環(huán)境的適應(yīng)程度，適應(yīng)度函數(shù)是用來評價適應(yīng)度大小的函數(shù)。本研究主要是使尿素泵流道塊裝配線平衡率最大化的同時尋找最小工位數(shù)，且裝配線的平滑性指數(shù)最低，因此對應(yīng)的適應(yīng)度函數(shù)為：

Fit=Fit1+Fit2（8）

Fit1=Rc（9）

Fit2=（10）

Fit2中分母加0.01是為了讓分母不為0。

（4）選擇。選擇是指在適應(yīng)度評估的基礎(chǔ)上，選擇最優(yōu)的個體。本文采用的選擇方法是精英選擇法，即將當(dāng)前種群中評估適應(yīng)度最高的個體直接復(fù)制到新個體中，這樣能最大可能的保存優(yōu)秀個體。

（5）交叉。為了使上一代的優(yōu)良基因能更好地遺傳給下一代，本文選用次序交叉方法，該方法源于單點交叉法，具體步驟：①隨機生成交叉點位置。②將兩個個體I1、I2交叉點前的基因編碼進行互換得到兩個新個體I11、I21，然后刪除兩個新個體交叉點后的重復(fù)元素C1、C2得到新個體I12、I22。③將重復(fù)元素C1、C2分別插入個體I22、I12中，同時保證生成的新編碼序列滿足工序的優(yōu)先關(guān)系約束，得到新的交叉?zhèn)€體I3、I4。

（6）變異。變異主要是為了提高種群的多樣性，通過變異能得到更優(yōu)的新種群。本文采用位置變異法，該方法需要保證變異后的個體是按照裝配工序優(yōu)先關(guān)系所約束的順序進行排列。在染色體上隨機選擇一個變異點，將該變異點位置上的基因插入到染色體上的其它位置，使新生成的子代個體既不同于父代又滿足各工序優(yōu)先關(guān)系約束。

（7）終止條件及參數(shù)設(shè)定。根據(jù)對尿素泵流道塊裝配線的分析，終止代數(shù)取200，即算法在進化200代后結(jié)束，取節(jié)拍時間為60s，初始化種群規(guī)模為60，最優(yōu)個體數(shù)4，交叉概率0.6，變異概率0.05。

2.3計算結(jié)果

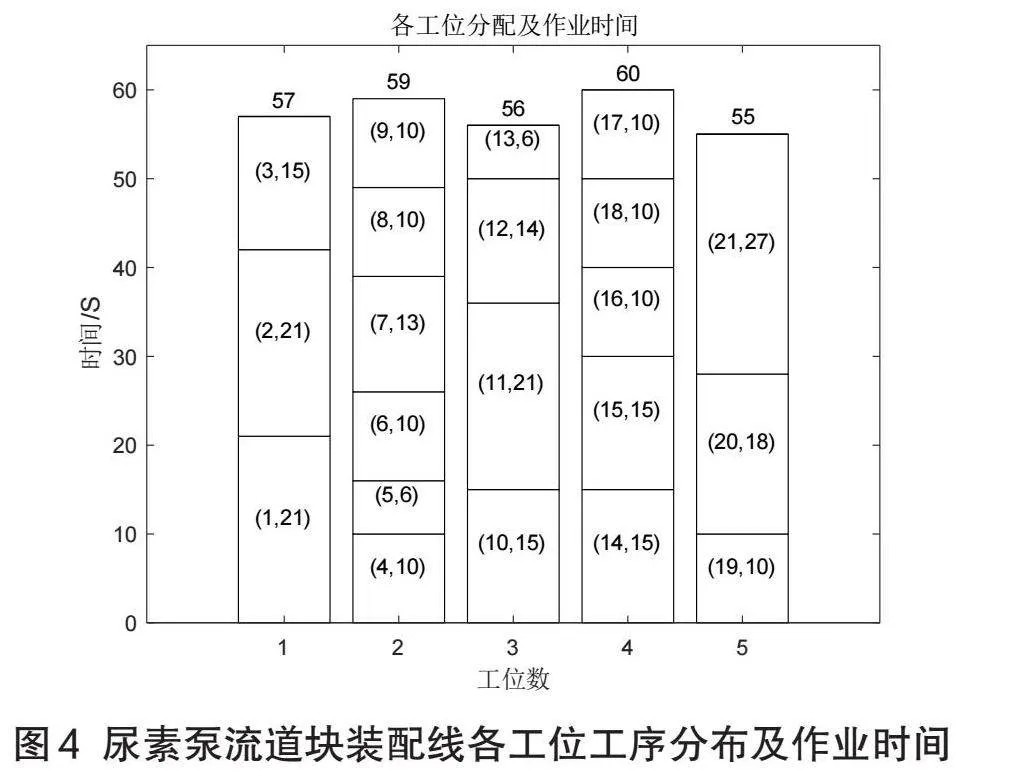
由遺傳算法對尿素泵流道塊裝配線進行優(yōu)化，借助matlab軟件，根據(jù)上文的參數(shù)設(shè)定，編寫程序進行求解，得到如圖4所示裝配線的工位工序分布及作業(yè)時間。根據(jù)運行結(jié)果可知，當(dāng)節(jié)拍時間為60s時，裝配線優(yōu)化后的最小工位數(shù)為5，每個工位分布情況為：J1={1，2，3}，J2={4，5，6，7，8，9}，J3={10，12，11，13}，J4={14，15，16，18，17}，J5={19，20，21}，各工位作業(yè)時間分別為：T1=57s，T2=59s，T3=56s，T4=60s，T5=55s。

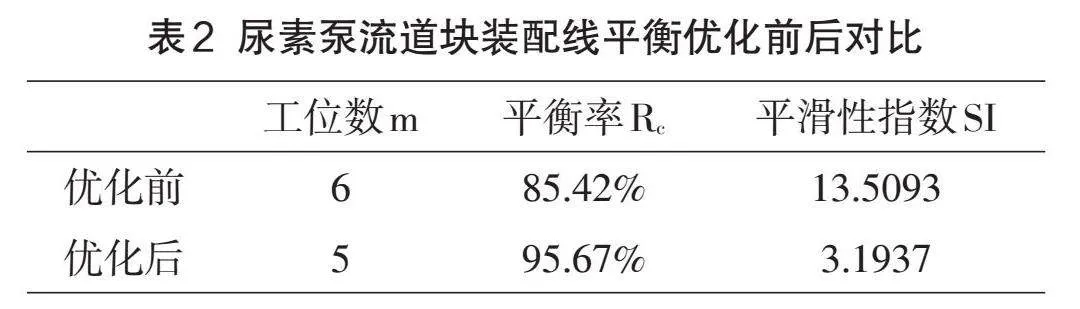
以上數(shù)據(jù)代入（1）（2）式可計算得到裝配線的平衡率Rc=95.67%，平滑性指數(shù)SI=3.1937。經(jīng)過對比分析，如表2所示，可知裝配線經(jīng)過優(yōu)化后平衡率和平滑性指數(shù)均得到明顯改善，因此，該裝配線平衡問題的優(yōu)化是有效可行的。

3 Flexsim仿真分析

3.1模型建立及參數(shù)設(shè)置

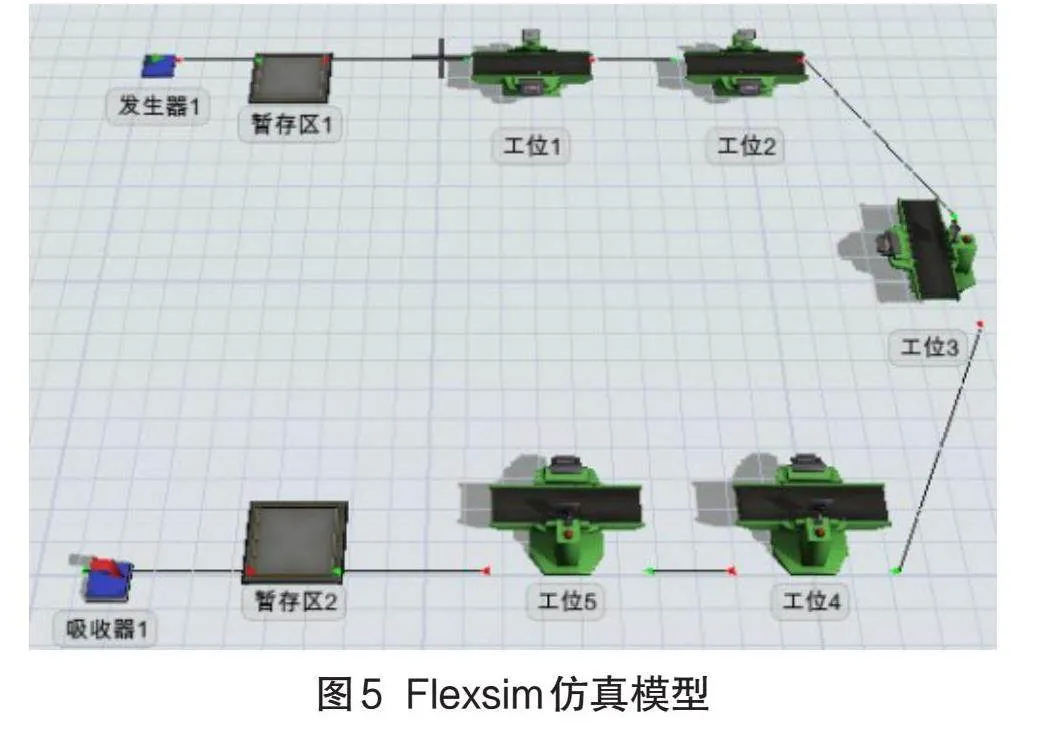
Flexsim軟件是一款主要用于離散系統(tǒng)建模與仿真的軟件[11]，本文采用該軟件進行尿素泵流道塊裝配線仿真，模擬其運行狀況。首先按照上文計算后的結(jié)果進行裝配線模型布局，裝配線共有5個工位，設(shè)置5個處理器來模擬各工位的裝配作業(yè)。還設(shè)置有2個暫存區(qū)，分別模擬零部件上線前和完成裝配后待下線的暫存區(qū)域。另外裝配線上還有一個發(fā)生器和一個吸收器，用發(fā)生器創(chuàng)建臨時實體模擬上料，臨時實體在裝配線上流動代表待裝配的中間產(chǎn)品，吸收器代表產(chǎn)品裝配完成后運輸下線。各個實體之間通過A連接。

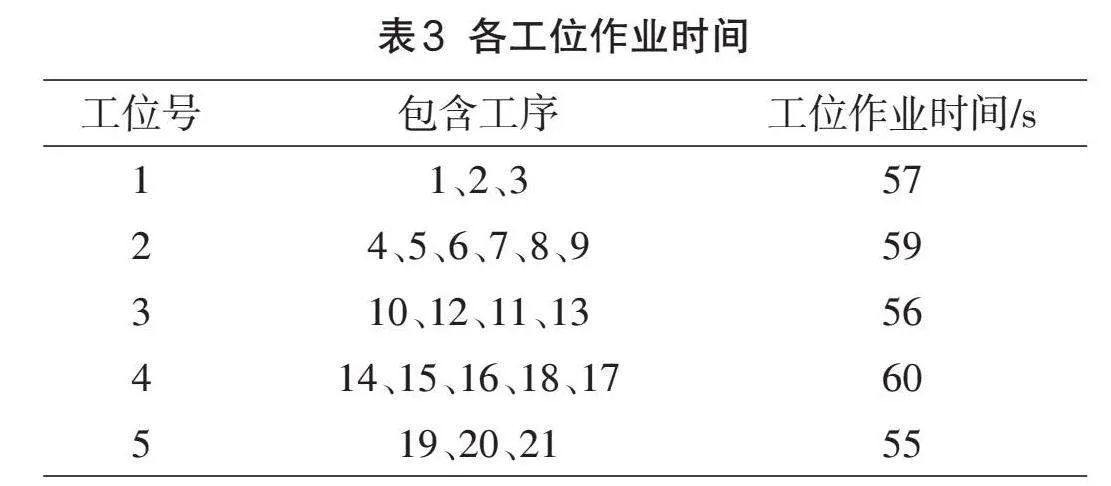
設(shè)置發(fā)生器到達時間間隔為節(jié)拍時間60s，暫存區(qū)最大容量為1000，處理器的加工時間按照計算結(jié)果中的各工位作業(yè)時間進行設(shè)置，如表3所示，吸收器表示成品下線，采用默認設(shè)置。生產(chǎn)線運行時間為企業(yè)一天有效工作時間7h，整個裝配線模型如圖5所示。

3.2仿真結(jié)果

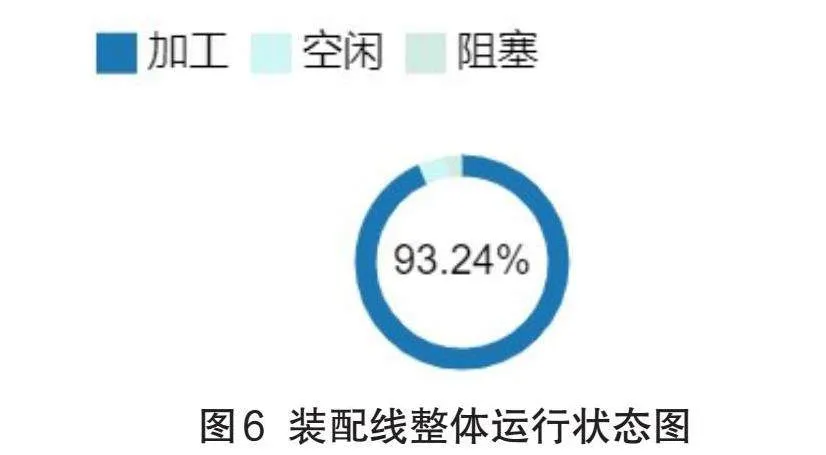
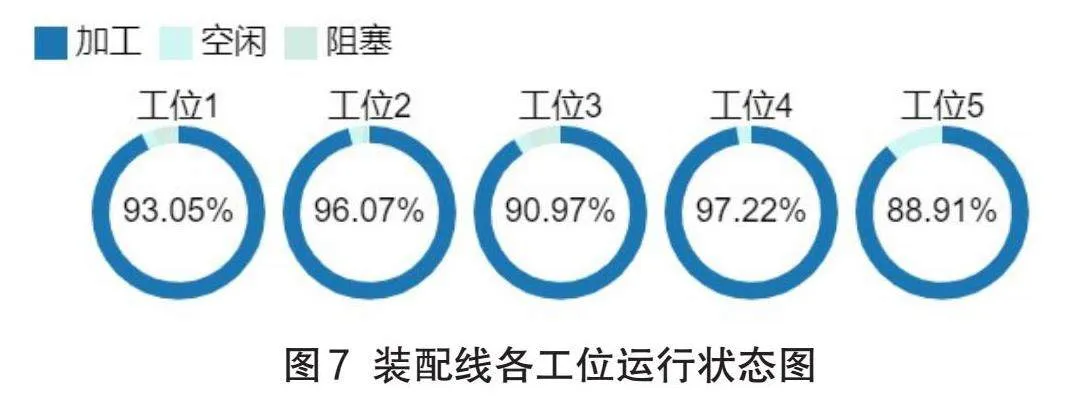
Flexsim軟件可以輸出多種裝配線生產(chǎn)狀態(tài)的數(shù)據(jù)。圖6為裝配線整體運行狀態(tài)圖，圖7為裝配線各工位運行狀態(tài)圖。由圖可知優(yōu)化后的裝配線總體利用率為93.24%，達到較高水平，各工位的利用率也較高，且堵塞和空閑時間較少。而裝配線的總產(chǎn)量可通過吸收器的輸入?yún)?shù)得知為407，基本達到預(yù)期的產(chǎn)量要求。

因此仿真驗證了該裝配線的優(yōu)化方法是合理且有效的。但在仿真運行過程中還發(fā)現(xiàn)了一些問題，如工位3的阻塞率較其它工位都高，工位5的利用率還未達到90%，這些都有繼續(xù)改善的空間，可作為下一輪研究的重點，這里不再進行展開分析。

4結(jié)語

提高裝配線平衡率是各生產(chǎn)企業(yè)日益重視的問題，本文以尿素泵流道塊裝配線為研究對象，描述了裝配線平衡問題，分析其工藝流程和工位現(xiàn)狀。在已知生產(chǎn)節(jié)拍的條件下，以最大平衡率為目標(biāo)函數(shù)建立數(shù)學(xué)模型，利用遺傳算法進行優(yōu)化，并借助matlab軟件對模型求解，最后通過Flexsim軟件進行裝配線仿真模擬，驗證了模型和算法的正確性及合理性。對比優(yōu)化前后的結(jié)果表明，裝配線的工位數(shù)較優(yōu)化前減少一個，平衡率由85.42%提升到95.67%，平滑性指數(shù)也大幅度下降，合理的工序分配和布局使裝配線的總體利用率也達到90%以上。總的來說，該優(yōu)化方法是有效的，但同時也發(fā)現(xiàn)了其它問題，為之后的研究提供了方向。本文將遺傳算法與Flexsim仿真結(jié)合解決裝配線平衡問題的方法，對企業(yè)的裝配線平衡改善也有一定的借鑒意義。

參考文獻：

[1]MENG K，TANG Q H，ZHANG Z K，et al.Solving Multi-objective Model of Assembly Line Balancing Considering Preventive Maintenance Scenarios Using Heuristic and Grey Wolf Optimizer Algorithm[J].Engineering Applica?tions of Artificial Intelligence，2021，100（4）：104183.

[2]LEE A H I，KANG H Y，CHEN C L.Multi-Objective Assem?bly Line Balancing Problem with Setup Times Using Fuzzy Goal Programming and Genetic Algorithm[J].Engineering Applications of Artificial Intelligence，2021.

[3]黃鵬鵬，郭煜，程洋.基于改進GA的血透管裝配線平衡優(yōu)化[J].制造業(yè)自動化，2020，44（6）：55-58.

[4]鄧超，胡瑞飛，蔣捷峰，等.考慮工人分配的多目標(biāo)裝配線平衡優(yōu)化[J].組合機床與自動化加工技術(shù)，2021，（06）：116-121.

[5]邱德元，賈華東.基于IE技術(shù)的托輪裝配線線平衡研究[J].中國工程機械學(xué)報，2019，17（6）：519-522.

[6]李明，包建軍，袁逸萍.基于改進遺傳算法的多目標(biāo)裝配線平衡優(yōu)化研究[J].機械設(shè)計與制造，2022（4）：204-207.

[7]張文修，梁怡.遺傳算法的數(shù)學(xué)基礎(chǔ)[M].西安：西安交通大學(xué)出版社，2003.

[8]杜利珍，張亞軍，董理，等.基于改進果蠅算法的第一類裝配線平衡率優(yōu)化[J].組合機床與自動化加工技術(shù)，2023（1）：184-187.

[9]ZHANG Z K，TANG Q H，LI Z X，et al．An Efficient Migrat?ing Birds Optimization Algorithm With Idle Time Reduc?tion for Type-ⅠMulti-manned Assembly Line Balancing Problem[J].Journal of Systems Engineering and Electron?ics，2021，32（2）：286-296.

[10]來阿娟.裝配線平衡問題建模與求解[D].長安大學(xué)，2014.

[11]張國輝，張凌杰.基于Flexsim仿真技術(shù)的混合裝配線平衡優(yōu)化[J].組合機床與自動化加工技術(shù)，2016（6）：131-133.

Research on Assembly Line Balancing Based on Genetic Algorithm and Flexsim Simulation

LI Jin，WU Xiao，F(xiàn)ANG Chuqiao，WANG Shaoxiang

（School of Mechanical Engineering and Automation，Wuhan Textile University，Wuhan Hubei 430200，China）

Abstract：Aiming at solving the problem of low balance rate and unbalanced job distribution of urea pump runner block assembly line in a company，a mathematical model aiming at maximum balance rate was established.Genetic algorithm was used to optimize the model，and the rationality and reliability of the optimization scheme was verified by Flexsim simulation software.The research shows that when the beat of the urea pump runner block assembly line is determined，the minimum number of stations is 5，the assembly line balance rate is the highest，the smoothness index is the lowest.And the software simulation results show that the utilization rate of each station of the assembly line is high，which verifies the feasibility of the assembly line improvement scheme.

Keywords：assembly line balancing;genetic algorithm;optimization;Flexsim simulation

（責(zé)任編輯：李強）