“幾倍”不是“幾個幾”

“倍的認識”是人教版三年級上冊第五單元的內容。可以說，“倍”的認識是小學階段“數概念”思維水平的一次重要提升，它使數從表示具體的“量”上升為表示抽象的“率”。建立好“倍”的概念，將為后續學習“零點幾倍”“幾分之幾”“百分之幾”打下堅實的基礎。

現實教學中，大部分老師把“幾倍”與“幾個幾”等同起來，客觀上降低了學生的思維難度。但“幾倍”與“幾個幾”是完全相同的概念嗎？這恐怕值得商榷。

一、“幾倍”與“幾個幾”的聯系

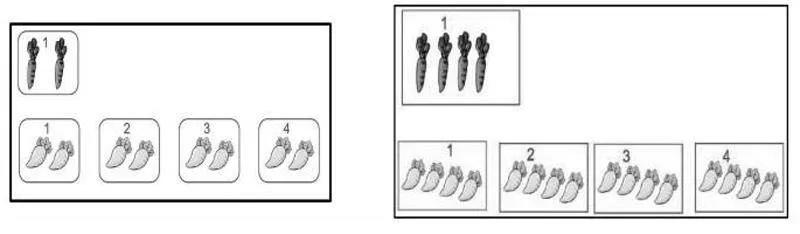
關于三年級“倍的認識”這節課的教學，很多教師覺得完全不費吹灰之力就能讓學生掌握，只要把之前乘法學習中的“幾個幾”學好了，在這里換個說法就是“幾倍”。教材的編排也是在學生學習了乘法和除法的基礎上來學習“倍的認識”，通過借助“幾個幾”來降低學習的難度。（如下圖）

教學時，老師們通常先對蘿卜進行分類計數——紅蘿卜有6根，胡蘿卜有2根；再通過圈圖、比較得出“胡蘿卜是1個2根，紅蘿卜是3個2根，我們就說紅蘿卜是胡蘿卜的3倍”。在此基礎上，學生很快就能遷移得到“白蘿卜有5個2根，白蘿卜就是胡蘿卜的5倍”。至此，大部分同學都會表示蘿卜間的倍數關系了，這時教師只要再通過幾道變式練習強化一下“幾個幾”和“幾倍”的聯系，就能讓幾乎全班同學在各類習題中順利過關。

用“幾個幾”來理解“幾倍”，既體現了知識的正向遷移價值，又提高了學習效率，似乎是一個不錯的辦法。但有的學生在判斷上圖紅蘿卜的根數是胡蘿卜的幾倍的時候，把兩根胡蘿卜也看作“1個2”，這樣就一共有“4個2”，從而得出“紅蘿卜的根數是胡蘿卜的4倍”這樣的錯誤結論——因為在學生初次學習乘法意義“幾個幾”的時候，都是從“第一份”數起的，在學習“幾倍”的時候，也會自然而然地把原來學習的經驗“遷移”到這節課中。

由此可見，“幾倍”就是“幾個幾”的理解方法似乎存在思維上的漏洞。

二、“幾倍”與“幾個幾”的區別

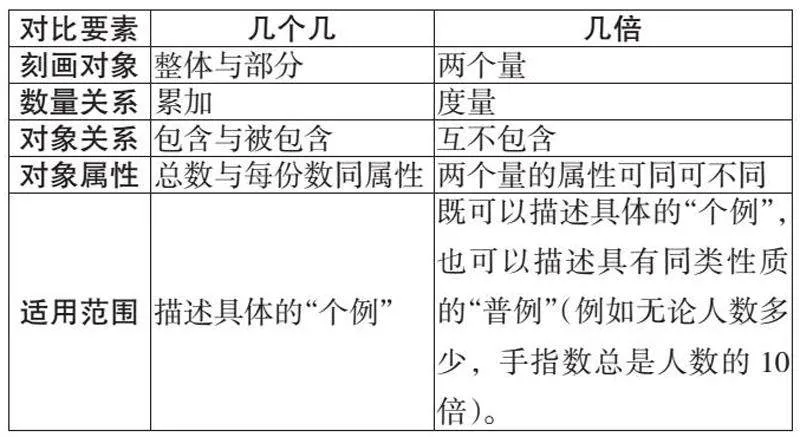
從最淺顯的生活經驗可以想得到，“幾倍”與“幾個幾”還是有著本質的區別的，具體的比較結果如下表：

由上表可見，“幾倍”與“幾個幾”有著本質的區別。用“幾個幾”來理解“幾倍”，表面上看似充分發揮了舊知識向新知識的遷移作用，提高了所謂的課堂教學效率。但卻因言害意，降低了學生的思維水平，難以深入理解“倍”的概念本質。

三、深入理解“幾倍”的實踐探索

深入理解“倍”的本質，需要循序漸進、展開推理、逐步抽象，形成一個完整的思維閉環。

1. 明確“倍”是比出來的

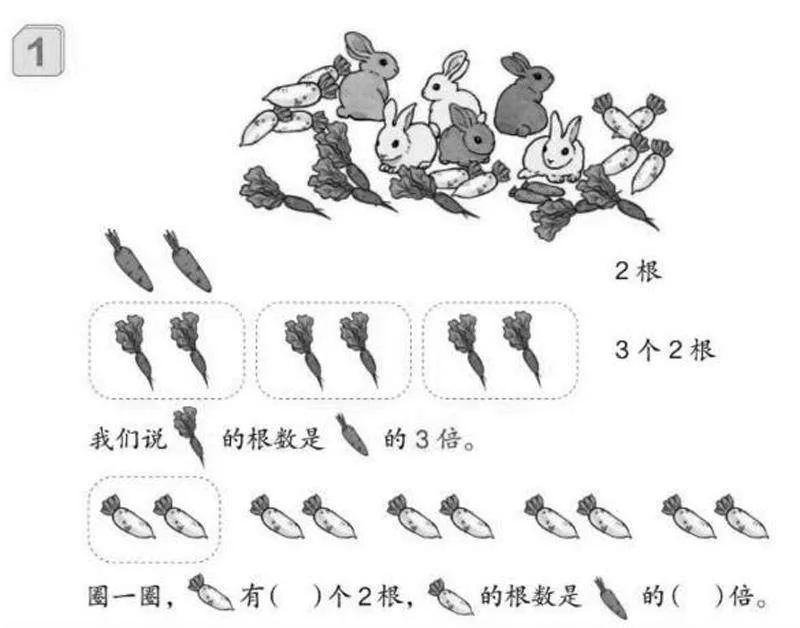
“幾個幾”是“數”（shǔ）出來的，而“幾倍”是“比”出來的。它描述的是兩個量之間的比較結果——而這種比較不同于一年級所學的“相差數量比”（其結果是一個具體的相差量），而是一種“包含份數比”（其結果是較大數包含幾份相當于較小數的量）。“幾個幾”在視覺上是由幾個零散的“部件”組成一個更大的“群體”，而“幾倍”在視覺上是用較小的一個數作為“尺子”去度量一個更大的“對象”。

教學中，老師可以通過圈一圈、數一數的方式，讓學生逐步明白“倍”是比出來的——它是兩個量之間的關系，所以不能單獨說某個數是“幾倍”。再通過PPT動畫演示，發現每比較一次都是“尺子”與“對象”的一部分“重合”，所以在描述“幾倍”的時候，不包括“尺子”（一倍數）。（如下圖）

2. “一倍數”是認識“倍”的根本

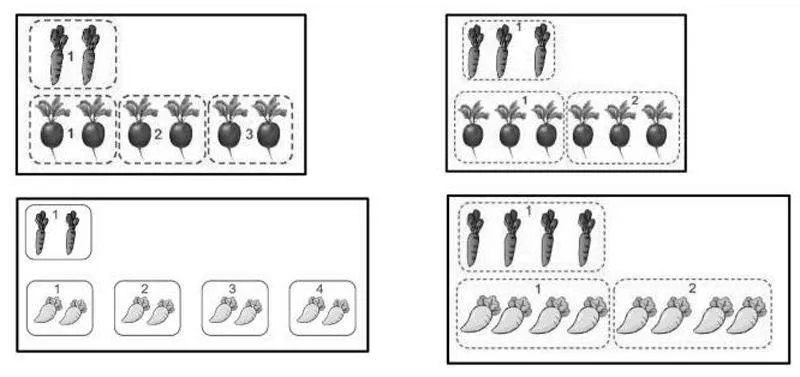
同樣是紅蘿卜和胡蘿卜做比較，6根紅蘿卜是2根胡蘿卜的3倍，6根紅蘿卜是3根胡蘿卜的2倍。紅蘿卜的根數并沒有發生變化，變化的是“一倍數”，一倍數是“幾”，就要用這樣的“標準”到對象中去“度量”，度量得幾次，就說對象是標準的“幾倍”。（如下圖）

縱向來看，同樣是得到了“2倍”。6根紅蘿卜是3根胡蘿卜的2倍，8根白蘿卜是4根胡蘿卜的2倍。都是把胡蘿卜的數量看成一倍數去度量，在紅蘿卜或白蘿卜中都分別度量得兩次，所以倍數都是2。不難發現，倍數是幾，其實和具體的蘿卜數量無關，只和“度量”得到的次數有關。

所以說，“幾倍”是從“一倍”開始的，“一倍”的標準是什么樣的，就按照這樣的標準在較大數中“一倍”“一倍”地比下去。“一倍數”是認識“幾倍”的根本。

3. “倍數”學習中的“變”與“不變”

在上面的例子中，“一倍數”不變的情況下，在越大的對象中比出來的倍數就越多，反之則越少。在對象相同的情況下，“一倍數”（尺子）越大比出來的倍數就越少，反之則越多。

6根紅蘿卜是2根胡蘿卜的3倍，8根白蘿卜是2根胡蘿卜的4倍，“一倍數”不變——都是2，測量的對象變大了，測得的倍數也就多；而當對象不變都是8時，一倍數是2，能比出4倍，一倍數是4時，就只能比出2倍了。

但也有不變的情況。就是當“一倍數”和對象都按照相同的倍數擴大或縮小的時候，比出來的倍數是相同的。（如下圖）

8根白蘿卜是2根胡蘿卜的4倍，當胡蘿卜和白蘿卜的數量都增加到原來的2倍時，16根白蘿卜仍然是4根胡蘿卜的4倍，倍數不變——用“大尺子”測量“大對象”與“小尺子”測量“小對象”，得到的結果相同。

通過“變”與“不變”的操作、觀察與思考，學生終于體會到“倍”是兩個數相比得到的一種抽象的關系（率），與具體的數量沒有關系。

四、“幾倍”在生活中的實際應用

學習這么抽象的“倍”，有什么用呢？用途大致有三：

其一，簡化數量關系。比如某位打字員錄入1500字的文稿需要11分鐘，他以同樣的速度錄入3000字的稿件需要多少分鐘？因為第二份稿件的字數是第一份稿件的兩倍，第二次的耗時自然也是第一次的兩倍，所以需要22分鐘。

其二，揭示某種規律。比如在配置糖水的時候，水的數量與糖的數量相比得出的“倍數”其實意味著糖水的甜度。無論糖與水的具體數量如何，只要“倍數”相同則兩杯糖水的甜度相同。

其三，奠基后續學習。較大數與較小數相比的結果是一個“倍數”（強比）；較小數與較大數相比的結果是一個“分率”（弱比）。它們形式不同，本質相通。對“倍”的本質意義理解到位了，“分率”的意義理解，也就是水到渠成之事。

由此可見，“幾倍”不是“幾個幾”，值得我們下大功夫引導學生理解其本質含義。

【注：本文系2022年度云南省教育科學規劃項目“基于核心素養的小學生推理意識培養的策略研究”（批號：BFJC22020）階段性研究成果】