巧用牛頓第二定律解決動力學中的瞬時性問題和臨界問題



【摘要】對于斜面上物體的運動可先分析給定物體的受力情況,然后應用牛頓第二定律求出加速度,再分析物體的運動過程,最后得出物體的運動情況.對于瞬時加速度問題,強調細繩剪斷瞬間的受力變化和加速度.對于探討疊加體系統臨界值問題,可先用隔離法求臨界加速度,再用整體法求系統加速度,最后比較判斷相對滑動的解題思路.
【關鍵詞】高中物理;牛頓第二定律;解題技巧
1引言
牛頓第二定律是高中物理力學的核心內容.很多學生在解題過程中常常不知從何入手,常常混淆受力分析和運動分析導致題目出錯.如何步步為營,將復雜問題化繁為簡并找到解題突破口是本文試圖探討的重點.通過梳理斜面、瞬時加速度、疊加體等三類典型問題的解題策略,幫助學生系統掌握分析方法,提高知識運用能力.
2斜面上的運動問題
例1如圖1所示,在傾角θ=37°的足夠長的固定斜面上,有一質量m=1kg的物體,物體與斜面間的動摩擦因數μ=0.5,物體受到平行于斜面向上的輕繩的拉力F=12N的作用,從靜止開始運動,經2s繩子突然斷了.已知sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2,求:
(1)第2s末繩子斷開時物體的速度大小;
(2)繩斷后經多長時間物體速度大小達到6m/s.
解析斜面上的運動問題屬于動力學基本問題.一般可先分析給定物體的受力情況,然后應用牛頓第二定律F=ma求出物體的加速度,接著分析物體的運動過程,最后得出物體的運動情況,如速度、位移等.反過來,在已知物體的運動情況下,如勻速運動或勻加速運動,可以通過運動學公式倒推出物體的加速度.運用牛頓第二定律a=Fm可以進一步求出物體所受的合外力,最后得到物體的受力情況.
(1)取向上為正方向,由牛頓第二定律得F-mgsin37°-μmgcos37°=ma1,解得a1=2m/s2.
2s末物體的速度為v1=a1t1=2×2m/s=4m/s.
(2)繩子斷裂后,物體沿斜面向上做勻減速運動,設運動的加速度大小為a2,由牛頓第二定律得mgsin37°+Mmgcos37°=ma2,解得a2=10m/s2.
t2=v1a2=0.4s,此后,物體沿斜面加速下滑,mgsin37°-Mmgcos37°=ma3,a3=2m/s2.
當速度達到6m/s時,時間t3=3s,所以總時間為3+0.4=3.4s.
3瞬時加速度問題
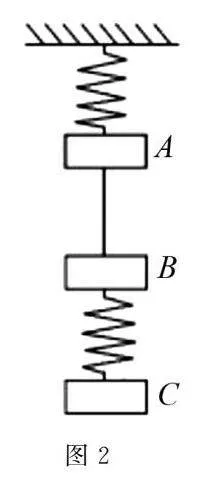
例2如圖2所示,有三個等質量的物體,分別標記為A、B、C.物體A的上方通過一根輕彈簧與天花板相連,物體B的下方也用一根相同的輕彈簧與物體C的上方相連.此外,在物體A和B之間還用一根細繩相連接.當整個系統處于靜止狀態時,假設突然將連接A、B兩物體的細繩剪斷,請問在剪斷的瞬間,三個物體A、B、C各自的加速度分別是()(規定加速度方向向下為正,重力加速度為g)
(A)-g,2g,0. (B)-2g,2g,0.
(C)-2g,2g,g. (D)-2g,g,g.
解析首先,在剪斷細繩之前,分別對物體A、B、C進行受力分析.通過平衡條件可以求出連接A和B的細繩所提供的拉力大小.接下來,設想細繩在某一時刻突然被剪斷,此時再次對三個物體分別進行受力分析.根據分析結果可以得出每個物體所受的合力.最后,利用牛頓第二定律,即可計算出物體A、B、C在細繩斷開瞬間各自的加速度.
具體到本題,在剪斷連接物體A和B的細繩之前,先分析一下物體B和C所受的合力.它們同時受到重力和細繩向上的拉力,由于整個系統處于平衡狀態,細繩的拉力大小必須等于兩個物體的總重力,即T=2mg.然后再來分析物體A,它受到重力、細繩的拉力以及彈簧的拉力.當細繩被剪斷的一瞬間,物體A和B之間的拉力驟然消失,但重力和彈簧的彈力仍然存在且保持不變.這時物體B所受的合力將等于2mg,方向豎直向下;而物體A所受的合力大小也為2mg,豎直向上.對于物體C而言,它所受的合力始終為零.根據牛頓第二定律,物體B將獲得2g的向下加速度,物體A將獲得2g的向上加速度,而物體C保持靜止,加速度為零.因此,正確答案為(B)選項.
4疊加體系統臨界值問題
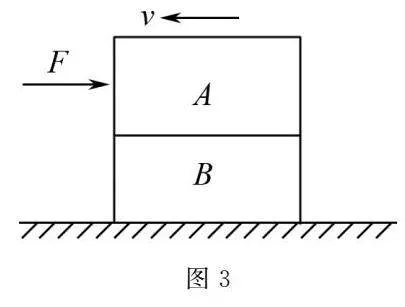
例3如圖3所示,兩個質量分別為M和m的物體A和B疊放在一光滑的水平面上以v的速度做勻速直線運動.A與B之間的動摩擦因數為μ.從時刻t=0開始,對物體A施加一個大小隨時間變化的推力F,其中F=kt,k為常數.求從推力開始作用到兩物體之間剛開始出現相對滑動所經歷的時間.
解析對于疊加系統可先用隔離法求出臨界加速度am,再用整體法假設疊加物體間無相對滑動,求解系統加速度a.下一步比較判斷當a≤am時無相對滑動,當a>am時有相對滑動,最后計算求解相關問題.
本題是關于牛頓運動定律綜合應用的題目,采用整體法和隔離法對物體進行受力分析是解答本題的關鍵.根據A、B間的最大靜摩擦力,隔離對B分析:求出最大加速度再對整體分析,求出最大推力,從而得出剛開始出現相對滑動所經歷的時間.
當A、B間的摩擦力達到最大時,f=μMg;對B隔離分析,最大加速度a=fm=μMgm.
對整體分析,F=M+ma=kt,解得t=(M+m)μMgkm.
5結語
通過以上分析,可見牛頓第二定律是解決此類問題的理論基礎.在實際解題過程中,需要認真審題,明確已知條件和求解目標,選擇合適的分析方法,如隔離法、整體法等,進行細致的受力分析,利用牛頓第二定律求解加速度,并結合具體情形確定速度和位移.解題時還要注意研究對象的選取、正負方向的規定、邊界條件的處理等細節問題.
參考文獻:
[1]葉來忠.牛頓第二定律在動力學問題中的應用[J].新課程,2021(49):124.
[2]古煥標.牛頓第二定律在動力學問題中的應用[J].中學生理科應試,2018(02):21-24.
[3]陳文靜,王世成.常見的涉及瞬時作用的物理問題分析[J].高中數理化,2024(16):16-17.
[4]蔡賽軍.巧用牛頓第二定律解瞬時問題[J].數理天地(高中版),2024(08):14-15.

