“五定”定乾坤



【摘要】帶電粒子在磁場中的運動是高中的重難點內容,學生在找圓心、做軌跡、找半徑、找圓心角以及求時間問題上困難重重.本文從構建情境、“五定剖析”及典型例題方面深入淺出地進行分析,希望給學生在這塊內容的學習上提供參考.
【關鍵詞】磁場;圓周運動;高中物理
帶電粒子在磁場中的運動經常出現在高考壓軸計算題中,是學生學習的難點.突破這類問題的關鍵是學會做粒子運動軌跡,并巧妙構建幾何關系,利用題中的長度和角度求解軌跡半徑,同時需要知道速度偏轉角、圓心角、弦切角之間的關系,這樣可以提高解題效率,達到事半功倍的效果.
1構建情境——提供鋪墊
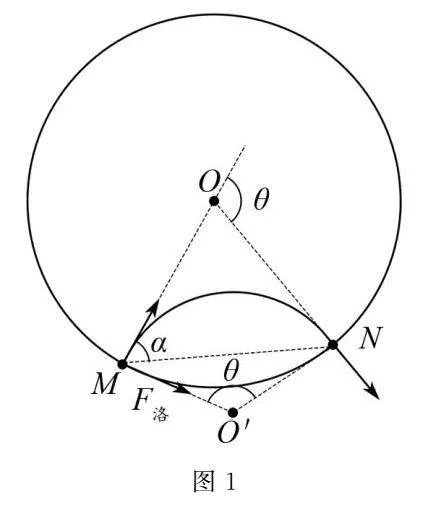
如圖1所示,有一垂直紙面向里,半徑為R的圓形磁場,磁感應強度為B,有一帶電量為-q,質量為m的粒子從M點正對圓形磁場的圓心射入,經磁場偏轉后從N點背離圓心射出,粒子進出磁場的速度的偏轉角為θ,弦切角為α,不計粒子的重力.
2方法介紹——“五定剖析”
一定軌跡據左手定則可得帶電粒子的軌跡,如圖1所示.
二定圓心作入射速度和出射速度的垂線相交于O′點,則O′點為粒子在圓形磁場中做圓周運動的圓心;或作入射速度的垂線及入射點和出射點的連線的中垂線的交點O′,O′點即為粒子在圓形磁場中做圓周運動的圓心.
說明根據需要合理選擇帶電粒子在磁場中的運動軌跡和軌跡的圓心的確定順序,先確定圓心,再確定軌跡更方便處理問題.
三定“圓心角”速度的偏轉角等于圓心角,圓心角為弦切角的2倍,即θ=2α.在實際應用中,在“四定半徑”中如果用三角函數解直角三角形需要先求出圓心角,如果不用三角函數解直角三角形,而是用勾股定理解直角三角形時往往不需要先求圓心角.
四定半徑方法1公式法
帶電粒子在磁場中受到的洛倫茲力提供粒子做圓周運動的向心力,則qvB=mv2r,所以r=mvqB.
方法2數學法
(1)利用三角函數求解:若能找到一個直角三角形的一個已知角(非直角)及一條邊長,可根據三角函數知識求帶電粒子在磁場中運動的軌道半徑r.在圖1中的直角三角形OMO′中,∠MO′O=θ2,MO=R,所以軌道半徑為r=Rcotθ2.
(2)利用勾股定理求解:若能找到一個直角三角形,但無已知角,往往可利用勾股定理建立方程求帶電粒子在磁場中運動的半徑;通常公式法和幾何法在同一題目中需同時使用,利用兩種方法求出的半徑r建立方程,再求其他物理量.
五定時間方法1
t=θ2πTT=2πmqB,帶電粒子在磁場中的運動時間t和粒子在磁場中運動的速率v的大小無關.此方法除了求帶電粒子在磁場中運動的時間t,通常還在比較不同速率v的粒子在同一磁場中運動的時間長短問題時使用.
方法2
t=sv,s為帶電粒子在磁場中運動通過的弧長,若帶電粒子速率v相同,粒子在磁場中通過不同的弧長s,則所用時間t不同.此方法除了求帶電粒子在磁場中運動的時間t,還在處理帶電粒子在磁場中運動的時間極值時使用.例如,在某一平面內速度大小相等的粒子在某一圓形磁場中運動時,圓形磁場的直徑對應的粒子的軌跡所用時間最長;在同一平面內從同一點向各個方向發出的速度大小相等的能到達同一條直線的粒子中,發射點到直線的垂線段對應的軌跡所用時間最短.
3“五定”定乾坤—例題精析
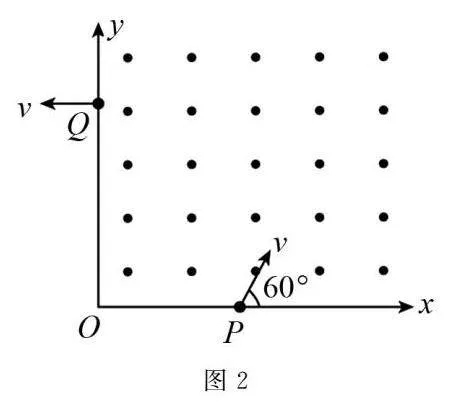
例題如圖2所示,一個質量為m、電荷量為q、不計重力的帶電粒子從x軸上的P點以速度v沿與x軸正方向成60°的方向射入第一象限內的勻強磁場中,并恰好垂直于y軸從Q點射出第一象限.已知OQ=a,則()
(A)粒子帶正電.
(B)粒子運動的軌道半徑為233a.
(C)勻強磁場的磁感應強度為B=3mv2qa.
(D)粒子在第一象限中運動的時間為t=43πa9v.
詳解一定軌跡根據左手定則可知,該粒子帶負電,故(A)錯誤.
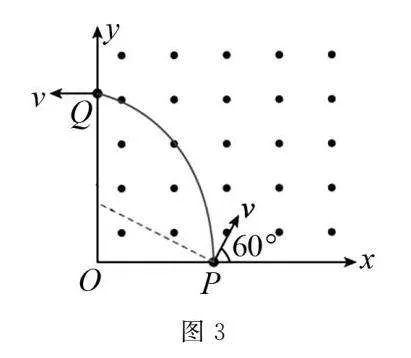
二定圓心做出粒子在磁場中的運動軌跡如圖3所示.
三定半徑由幾何關系可得R+Rcos60°=a,解得R=23a,故(B)錯誤.
根據洛倫茲力充當向心力有Bqv=mv2R,解得B=3mv2qa,故(C)正確.
四定圓心角根據幾何關系可知粒子在磁場中轉過的圓心角為2π3,而粒子做圓周運動的周期T=2πRv,將R=mvqB代入可得T=2πmqB.
五定時間由此可得粒子在第一象限內運動的時t=13T=13×2πmqB=2πm3q×2qa3mv=4πa9v,故(D)錯誤.
故選(C).
點評根據題中兩個速度方向確定兩個洛倫茲力方向,兩個洛倫茲力交點即為圓心,進而確定運動軌跡以及圓心角.“五定”是處理帶電粒子在磁場中運動的一般過程,在實際應用中需根據實際需要合理選擇“五定”的使用順序.
4結語
帶電粒子在磁場中的運動對學生綜合能力要求較高,需要綜合應用物理、數學知識解決問題,需要學生根據題中條件確定運動軌跡,進而找出圓心、半徑、圓心角以及運動時間.利用幾何關系求解半徑時,要注重培養信息分析能力和作圖能力,可以根據提取題目中的關鍵條件求解,提高處理復雜問題的能力,更好適應新高考的要求.

