帶電粒子在電場中運動問題的解題策略探究


【摘要】本文探討在高中物理解決帶電粒子在電場中運動問題的幾種有效策略,包括利用運動分解法處理曲線運動問題、用功能關系法分析電場力做功的特點,以及用極限思想探討臨界狀態等.在解帶電粒子在電場中運動問題時,教師應引導學生綜合運用物理知識進行分析探究,關注學生在解題過程中的思維方式,幫助其形成科學的思維習慣,從而提高學生的解題能力.
【關鍵詞】帶電粒子;電場;解題策略
1引言
帶電粒子在電場中的運動是高中物理電磁學部分的重要內容,涉及電場力、電勢能等基本概念和規律的綜合應用.學生在解決此類問題時常常遇到困難,原因在于問題情境的多樣性和物理學科知識的綜合性.因此,總結帶電粒子在電場中運動問題的解題策略可以幫助學生提高分析問題和解決問題的能力.
2用運動分解的思想處理帶電粒子的曲線運動.
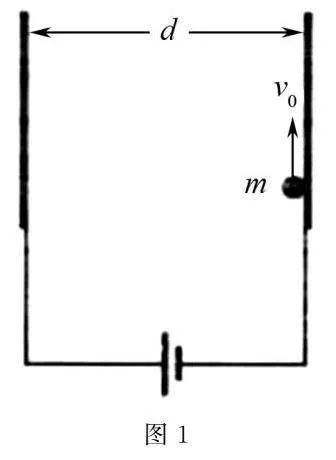
例1如圖1所示,一個質量為m、電荷量q的帶負電小球在平行板電容器右板內側豎直向上拋出.電容器兩板間距為d,施加電壓U.小球最終落在電容器左側板的同一高度位置.求小球運動過程中到達的最大高度H以及初始拋出速度v0.
解析小球受重力和電場力的作用分別在豎直方向和水平方向做豎直上拋運動及初速度為零的勻加速直線運動,對兩個方向的運動分別根據運動學公式列式求解.
對于水平分運動,有d=12at2.
由牛頓第二定律有a=qUmd.
聯立解得t=2md2qU.
對于豎直方向分運動,有H=12gt22,
0=v0-gt2.
解得v0=gdm2qU,H=mgd24qU.
本題用到運動分解的思想,將小球的運動分解為豎直方向和水平方向.在處理帶電粒子在勻強電場或電場與重力場組成的復合場中做曲線運動時,一般將比較復雜的曲線運動分解為沿電場方向和垂直于電場方向的兩個分運動求解.
3用功能關系法處理相關問題
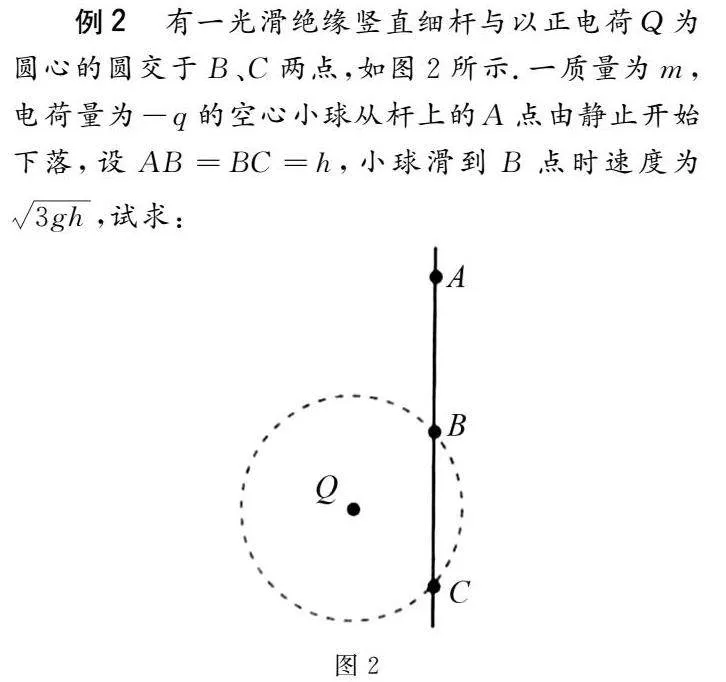
例2有一光滑絕緣豎直細桿與以正電荷Q為圓心的圓交于B、C兩點,如圖2所示.一質量為m,電荷量為-q的空心小球從桿上的A點由靜止開始下落,設AB=BC=h,小球滑到B點時速度為3gh,試求:
(1)小球滑至C點的速度;
(2)A、B兩點的電勢差.
解析(1)因B、C是在電荷Q產生的電場中處在同一等勢面上的兩點,即UBC=0,所以從B到C時電場對帶電小球所做的功為零.
由B→C,根據動能定理,
得mgh=12mv2C-12mv2B.
將vB=3gh帶入,得vC=5gh.
(2)由A→B,根據動能定理mgh+(-qUAB)=12mv2B.
故UAB=-mgh2q.
本題用到功能關系法.電場力做功只由始末位置的電勢差決定,與電荷經過的路徑無關,即WAB=qUAB,因此在處理粒子在均勻強電場或非均勻強電場中進行直線運動或曲線運動相關問題時,采用功能關系法都是一種行之有效的解題方法.
4用極限思想分析臨界問題
例3如圖3所示,一束電子流經U=5000 V加速電壓加速后,在距兩極板等距離處垂直進入平行板間的勻強電場,若兩板間距d=1.0 cm,板長l=5.0 cm.問:要使電子能從平行板間飛出,兩個極板上能加的最大電壓是多少?
解析求解帶電粒子在電場中運動的臨界問題時,關鍵是找到臨界狀態所對應的臨界條件,而臨界條件可以借助極限法進行分析.
①根據動能定理可得,電子在加速過程中有eU=12mv20,
②電子進入偏轉電場后可得l=v0t,
③進入偏轉電場后電子垂直于版面的加速度為a=Fm=eU′dm,
④偏距為y=12at2,
⑤當偏距y≤d2時,電子能從平行板間飛出.
聯立①~⑤可得
U′≤2Ud2l2=2×5000×1.0×10-225.0×10-22V=400V.
故要使電子能從板間飛出,所加電壓最大為400V.
本題用到極限思想,在給定的加速電壓下,偏轉電壓U′對電子在平行板間的偏轉距離有決定性影響.U′越大,電子的偏距就越大.當U′增大到一定值時,電子將恰好沿著極板邊緣飛出.這個臨界偏轉電壓就是題目所求的最大電壓.
5結語
解決帶電粒子在電場中運動問題需要綜合運用物理學科知識,靈活采取恰當的解題策略.其中,運動分解法、功能關系法和極限思想等,都是行之有效的方法.在教學實踐中,教師還應注重引導學生利用所學物理知識綜合分析問題的特點,進而選擇合適的解題策略.同時,要關注學生解題過程中的思維方式,適時給予引導,幫助學生梳理思路,培養科學的思維習慣.
參考文獻:
[1]曹莉.探討帶電粒子在電、磁場中的運動[J].數理化解題研究,2024(25):94-96.
[2]蔣金團,代朝榮.例析帶電粒子在圓形磁場中做圓周運動[J].數理化學習(高中版),2024(07):50-53.
[3]余勝強.帶電粒子在電、磁場中的運動分析[J].高中數理化,2023(24):13-14.
[4]陳豐波.學好電場“三條線”,解題變得不再難[J].高中數理化,2023(Z2):40-41.

