轉換法在高中物理解題中的應用

【摘要】高中物理主要研究自然界中的各種現象，包括聲、光、力、電等.在學習過程中，學生對如“力的作用”等抽象概念理解存在一定難度.此時，可使用轉換法將抽象問題轉換為具體問題，從而達到快速解題的目的.本文提出轉換思維方式、轉換研究對象兩種解題技巧，以期幫助學生實現快速準確解題.

【關鍵詞】高中物理；轉換法；解題技巧

在解題過程中，若按正常解法求解有難度時，可以利用轉換法，將不可見、不易見的現象轉換成可見、易見的現象，將陌生、復雜的問題轉換成熟悉、簡單的問題，將難以直接測量的物理量通過容易測量的物理量來間接測量.

1轉換思維方式解“力的作用”

在解決與“力的作用”相關的問題時，轉換思維方式是一種非常有效的策略.其要求學生從不同的角度審視問題，利用逆向思維、等效替代或其他非傳統的方法，理解和分析力的作用[1].

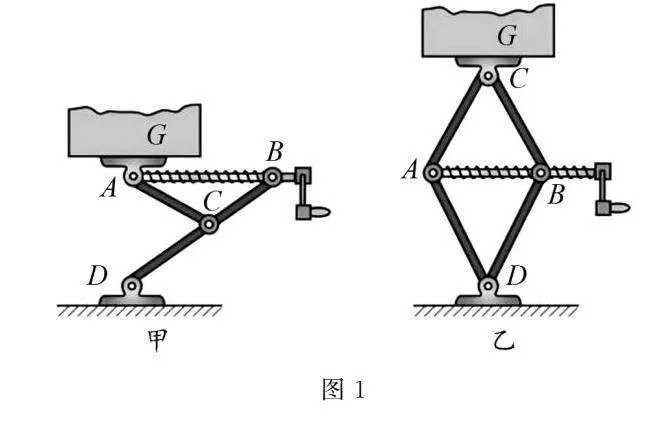
例1如圖1所示為汽車內常備的兩種千斤頂的原理圖，其中甲為Y形，乙為菱形，工作過程中，順時針轉動手柄，通過螺桿作用，AB兩點距離縮小，從而達到頂起重物G的目的.反之，逆時針轉動手柄，則會實現降低重物G的目的.若將重物G看作汽車，則能夠實現頂起車身，更換輪胎的目標.若此時汽車重為G，AC與AB之間的夾角為θ，則螺桿AB的拉力為多少？

解析根據題意分析，重物G與千斤頂間保持相對靜止，達到二力平衡狀態.若設想螺桿AB突發失效，平衡將被打破，重物G將不可避免地受到重力主導，開始自由下落.此情景清晰揭示了螺桿AB所施加的拉力在維持整個系統穩定與重物G位置不變中扮演著至關重要的角色，即它是實現物體平衡、防止重物下落的關鍵作用力.

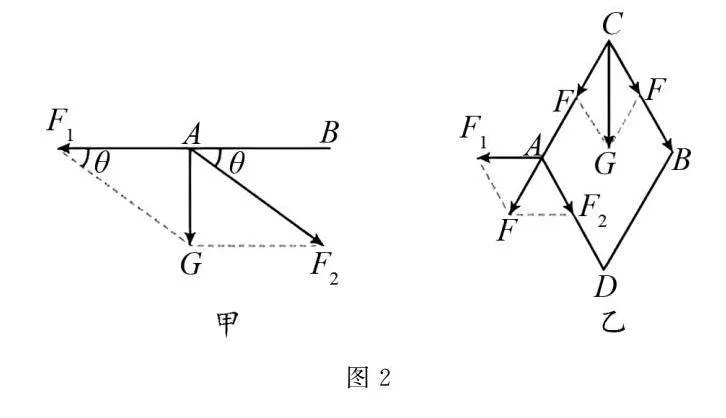
Y形千斤頂的簡化模型如圖2（甲）所示，可以將重物對A點的垂直壓力G，通過力的分解原理，轉化為兩個分力：一是沿螺桿方向的力F1，二是沿斜桿方向的力F2.兩個力與G共同構成一個平行四邊形.從圖中可以看出，F1和F作為G的分力，其合力與G等大反向，所以F1=Gcotθ.

對菱形千斤頂，根據力的實際作用效果，確定分力的方向，對力G進行二次分解，如圖2（乙）所示，G作用在C點，可分解為兩個均為F的分力，F作用在A點，又可分解為F1和F2兩個分力，其中F1為對螺旋桿的拉力.由于ACBD是一個菱形，根據力的三角形與幾何三角形相似可得，在C處可得F=G2sinθ，在A處可得F1=2Fcosθ，所以，F1=G2sinθ·2cosθ=Gcotθ，即Y形和菱形千斤頂螺旋桿AB的拉力均為Gcotθ.

2轉換研究對象解“力的作用”

在求解物理問題時，當存在兩個或兩個以上的物體時，首先要考慮的是研究對象問題.研究對象的正確選取，關系到解題過程的簡單與繁瑣，關系到解題的成敗，若選錯了研究對象，有時會出現根本無法求解的現象．但如果能轉換思維，合理改變研究對象，問題也就能得到順利解決.

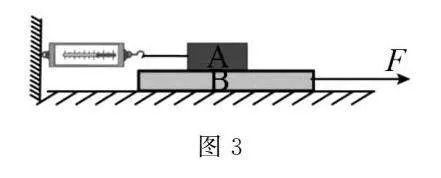
例2如圖3所示，A、B為重疊的兩木塊，木塊B在拉力F=6N的作用下，向右做勻速直線運動，此時連接木塊A的彈簧測力計示數為2N.則此時木塊A對木塊B的摩擦力大小為，地面對木塊B的摩擦力大小為.

解析本題考查的是對物體間相互作用力及摩擦力的應用.題干描述了A、B兩木塊在特定條件下的運動狀態及受力情況，要求分析兩個關鍵摩擦力：木塊A對木塊B的摩擦力，以及地面對木塊B的摩擦力.若逐個進行受力分析，則計算量較大.此時可以適當轉換研究對象，達到快速解題的目的.

木塊A在彈簧測力計的拉力和B對A的摩擦力的作用下保持靜止狀態，兩個力是一對平衡力，大小相等.此時彈簧測力計示數是2N，由此可知木塊B對木板A的摩擦力為2N；木塊A對木板B的摩擦力與木塊B對木板A的摩擦力是一對相互作用力，大小相等，所以，木塊A對木板B的摩擦力為2N.

在分析地面對木塊B的摩擦力時，則以木塊B為主要研究對象，進行受力分析，木板B在水平方向上受到拉力F和木塊A對木板B的摩擦力以及地面對木板B的摩擦力，其中拉力F水平向右，木塊A對木板B的摩擦力fA水平向左，木塊B向右做勻速直線運動，所以地面對木塊B的摩擦力f地水平向左，則根據二力平衡，則有fA+f地=F.

因為fA=2N，F=6N，所以f地=F－fA=6N－2N=4N.

3結語

綜上所述，轉換法在高中物理解題中，尤其在處理“力的作用”問題時，展現出獨特的優勢，其要求學生不拘泥于傳統思路，勇于探索新的視角、方法.通過轉換思維方式和研究對象，學生能夠將復雜、抽象的問題轉化為直觀、易解的形式，有效提升解題效率和準確性[2].掌握并靈活運用轉換法，不僅能夠培養學生的物理思維能力和創新能力，還能促進學生對物理概念及原理的深入理解，為后續的物理學習打下堅實的基礎.

參考文獻：

[1]高世明.轉換法在高中物理解題中的應用——以力的作用為例[J].數理化解題研究，2023（13）：128-130.

[2]曾令波.轉換法在高中物理解題中的應用[J].數理天地（高中版），2024（08）：45-46.