滾動軸承滾道故障演化的動力學建模與響應分析

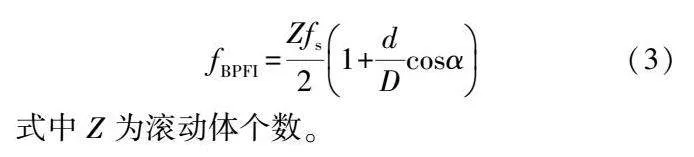
摘要：對滾動軸承滾道故障演化過程的振動特性及應力特性進行分析，在充分考慮徑向載荷、轉速、摩擦等影響因素的前提下，通過ANSYS/LS-DYNA建立滾動軸承的二維全柔性顯式有限元模型，進行外、內滾道故障演化情況的仿真分析。分析結果表明：計算得出的故障特征頻率與理論解誤差小于1%；隨滾道故障演化，軸承的振動響應及應力水平均升高；在相同故障尺寸下，內滾道故障對振動響應及應力的影響更大。

關鍵詞：滾動軸承；局部故障；動力學建模；LS-DYNA；響應分析

中圖分類號：TH133.33文獻標志碼：B文章編號：1671-5276（2024）06-0119-04

Abstract：To analyze the vibration and stress characteristics of the rolling bearing raceway fault evolution process， a two-dimensional fully flexible explicit finite element model of the rolling bearing is established by ANSYS/LS-DYNA with full consideration of radial load， rotational speed， friction and other influencing factors， and the simulation analysis of the outer and inner raceway fault evolution is carried out. The analysis results show that the error between the calculated fault characteristic frequency and the theoretical solution is less than 1%， the vibration response and stress level of the bearing increase with the evolution of the raceway fault， and under the same fault size， the influence of the inner raceway fault on the vibration response and stress is greater.

Keywords：rolling bearing; localized defect; dynamic modeling; LS-DYNA; response analysis

0引言

滾動軸承是旋轉機械的關鍵部件，其運行狀態直接影響旋轉機械的傳動精度及運行安全。據統計，有大約30%的旋轉機械故障是由軸承故障引起，且其中90%的軸承故障位于滾道上［1］。對含有滾道故障的軸承進行準確地建模與分析對認識其振動機制有重要意義。滾動軸承的建模經歷了靜力學、擬靜力學、擬動力學以及動力學4個階段。在采用解析法建立軸承模型時，通常伴隨著較多的簡化，如將材料考慮為剛體，忽略保持架的作用等。隨著商業軟件的發展，通過有限元方法建立滾動軸承的動力學模型，提取各部件的動力學響應，從而對軸承的響應特性及動態性能進行分析成為了一種高效的研究手段［2-3］。

目前關于軸承故障的研究主要集中在振動響應，而忽略了故障演化過程中應力的變化情況。滾動體與滾道之間循環交變的應力是導致軸承接觸疲勞、出現初始故障的直接原因。對滾道故障演化過程中的應力變化進行分析，有助于對其內部的動態性能及故障激勵機制的進一步認識。

1滾動軸承的運動學理論及有限元建模方法

1.1滾動軸承的運動學理論

一般情況下，滾動軸承在運轉過程中將外圈與軸承座固定，內圈與旋轉軸固定并同步旋轉，滾動體受保持架約束，沿滾道公轉的同時繞自身軸線自轉。保持架轉動頻率的計算方法如下：

式中：fs為旋轉軸轉動頻率；d為滾動體直徑；D為軸承的節圓直徑；α為接觸角。

當滾道發生故障時，滾動體經過故障位置會產生周期性的沖擊信號，外圈故障特征頻率fBPFO以及內圈故障特征頻率fBPFI的計算方法分別為：

式中Z為滾動體個數。

1.2正常滾動軸承的有限元建模

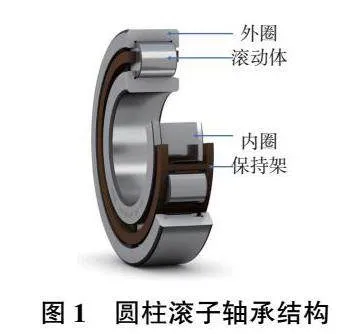
本文以NU202型圓柱滾子軸承為研究對象，其主要構成部件為外圈、內圈、滾動體及保持架，結構如圖1所示，主要設計參數如表1所示。

采用ANSYS/LS-DYNA建立軸承的二維有限元模型，LS-DYNA是著名的顯式動力學分析程序，能夠高效求解非線性動力學問題。二維有限元模型在滿足分析要求的同時，相比三維模型可大幅度減少計算資源。SINGH等［4-5］的研究表明：網格劃分導致的數值噪聲會對振動響應產生直接的影響，網格尺寸過大，產生接觸的各部件之間可能發生初始穿透，導致模型無法運算或計算結果的不準確。本模型中將內外滾道與滾動體接觸部分的網格進行局部細化，設定徑向游隙為0.01mm，兜孔間隙為0.05mm。模型的網格尺寸在0.01～0.30mm之間。

LS-DYNA中采取罰函數法來計算兩接觸表面之間的接觸關系，通過接觸算法來檢查每個時間步長下目標面與接觸面間是否出現穿透。在滾動體與內外滾道的接觸對中，滾動體表面為接觸面，內、外滾道為目標面，靜、動摩擦因數分別為0.10、0.05；滾動體與保持架的接觸對中，滾動體表面為接觸面，保持架為目標面，靜、動摩擦因數分別為0.05、0.02。

為模擬其運行工況，在外圈內表面以及內圈外表面建立剛性面，對外圈內表面剛性面施加全約束，對內圈外表面剛性面施加轉速及徑向載荷，載荷方向為y軸負方向，即重力方向。最終建立的模型如圖2所示，單元數為18 973，節點數為19 913。

1.3滾動軸承滾道故障演化有限元建模

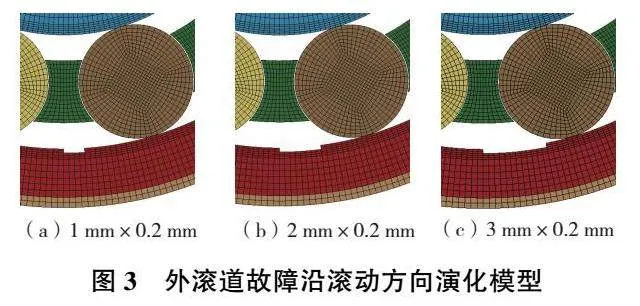
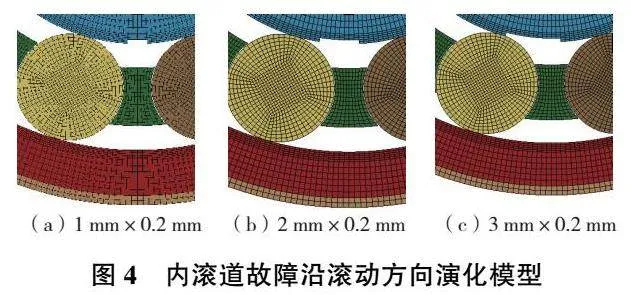
軸承已經產生表面剝落故障后，在滾動體運動的反復沖擊下，剝落沿滾動方向不斷拓展，依此建立外滾道及內滾道故障演化的模型，如圖3及圖4所示。故障寬度分別為1mm、2mm以及3mm，故障深度均為0.2mm。

2外滾道故障演化的振動響應及應力分析

對前文建立的外滾道故障演化模型進行求解分析，計算轉速為100rad/s，計算時長為0.20s。在此轉速下轉動頻率為15.92Hz，外圈故障特征頻率fBPFO的理論解為68.12Hz。

2.1振動響應分析

振動響應的采集位置為軸承外圈節點，由于有限元仿真計算結果不可避免地受到網格離散化帶來的數值噪聲的影響，因此對時域信號進行2 000Hz的低通濾波，并對濾波后的時域信號進行包絡分析，得到頻譜。無故障情況下，軸承的振動信號如圖5所示，無明顯沖擊特征。

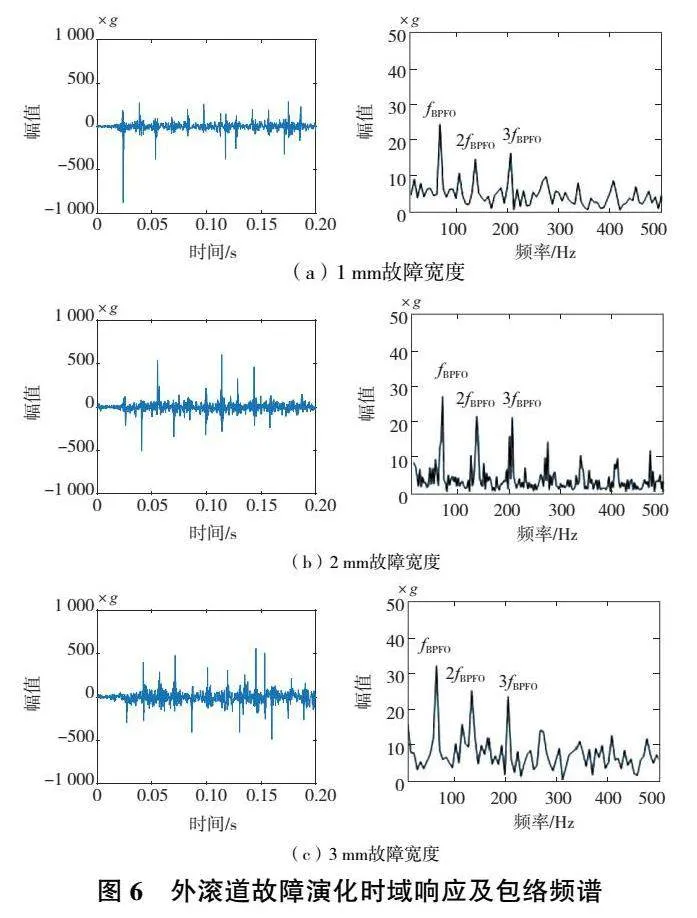
外滾道故障演化的時域響應及包絡頻譜如圖6所示。

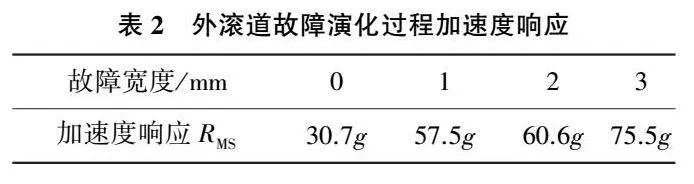
從圖6中能夠清晰地識別fBPFO（68.72Hz）及倍頻2fBPFO、3fBPFO…，且故障尺寸的變化不會導致頻率成分的變化。計算得出的fBPFO與理論解之間誤差為0.88%，可認為該模型能準確地模擬外滾道故障情況。加速度響應時域信號中幅值隨機波動較明顯，峰值的大小有較大的隨機性，因此采用對于軸承進行狀態監測時常用的指標方均根（RMS）進行分析。外滾道故障演化過程加速度響應的RMS在表2中給出，其中故障寬度0mm為軸承的正常狀態。隨外滾道故障演化，軸承的振動響應明顯增強。

2.2應力分析

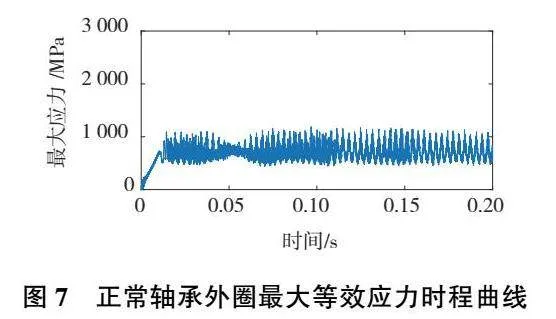
在軸承無故障情況下，外圈的最大等效應力時程曲線如圖7所示。

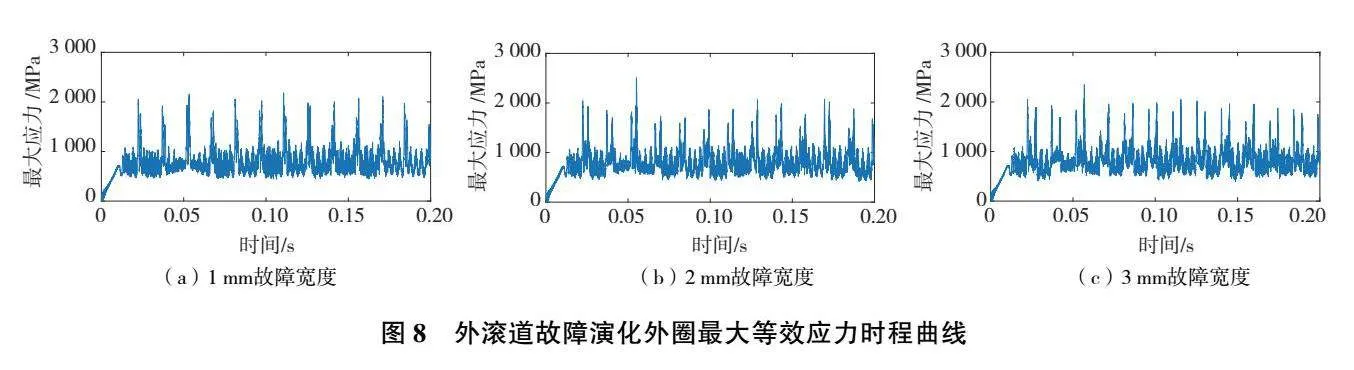
在外滾道故障演化情況下，各故障寬度下外圈最大應力時程曲線如圖8所示。

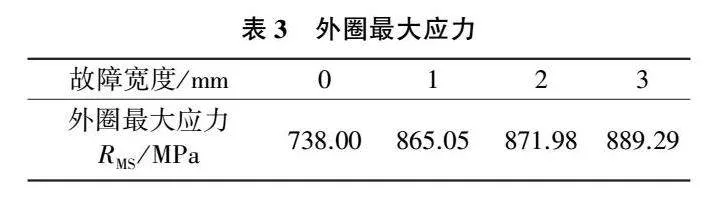
從圖8中可以發現，在外滾道故障狀態下，軸承外圈的最大應力同樣出現周期性沖擊，其沖擊時間間隔為1/fBPFO，證明外圈應力的波動是由于滾動體周期性地與故障位置產生沖擊。同樣采用RMS值對應力水平進行評估，從表3中可以發現，在外滾道故障演化時，外圈的等效應力水平有明顯增加。

3內滾道故障演化的振動響應及應力分析

考慮到內滾道故障時故障位置與旋轉軸同步轉動，故障位置時而處于承載區內，與滾動體碰撞產生明顯振動響應；時而處于承載區域外，與滾動體碰撞時振動響應不明顯。因此需要在考慮計算時長的情況下增加計算周期數，以獲取其周期特征。在進行內滾道故障仿真時，選擇計算轉速為200rad/s，計算終止時間延長至0.4s。在此轉速下轉動頻率為31.83Hz，內圈故障特征頻率fBPFI的理論解為213.90Hz。

3.1振動響應分析

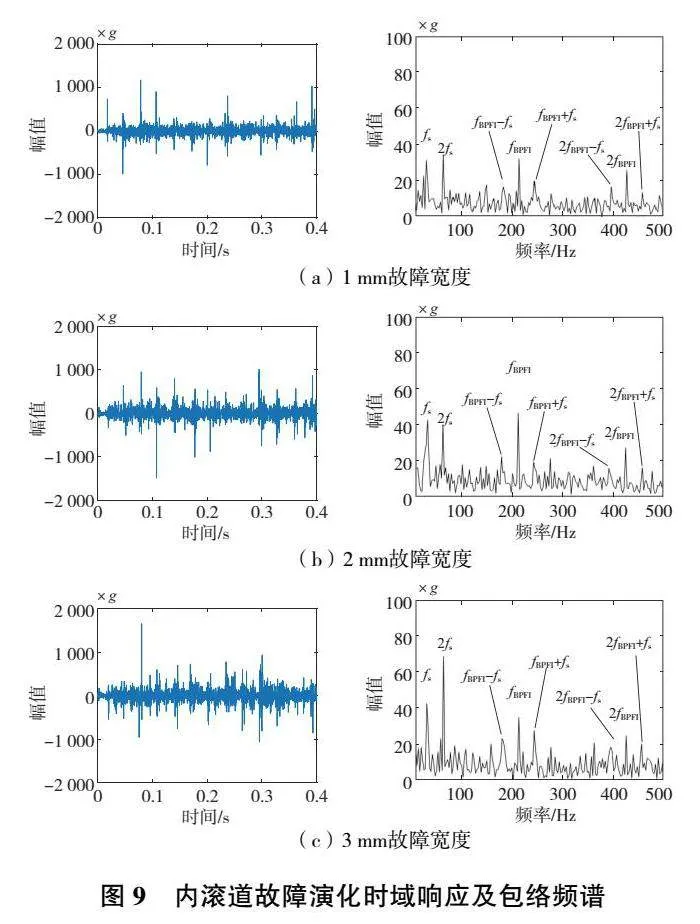
內滾道故障演化的時域響應及包絡頻譜如圖9所示。

相較于外滾道故障情況，在軸承內滾道存在故障時，其頻譜中頻率成分更加豐富，主要表現為fs及倍頻、 fBPFI（213.85Hz）及倍頻以及二者的調制頻率：fBPFI－fs、 fBPFI+fs、2fBPFI－fs、2fBPFI+fs等，同時故障尺寸的變化不會導致頻率成分的變化。計算得出的fBPFI與理論解之間誤差為0.02%，可認為該模型能準確地模擬內滾道故障情況。

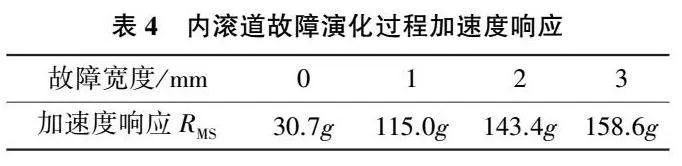
內滾道故障演化過程加速度響應的RMS值在表4中給出，隨故障演化，軸承的振動響應明顯增強。同時與表2對比可以發現，在相同故障尺寸下，故障發生于內滾道上時會引發更強烈的振動。

3.2應力分析

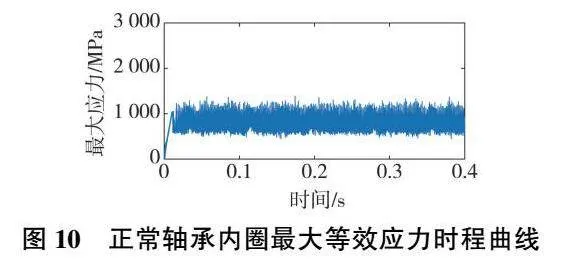
在軸承無故障情況下，內圈的最大等效應力時程曲線如圖10所示。

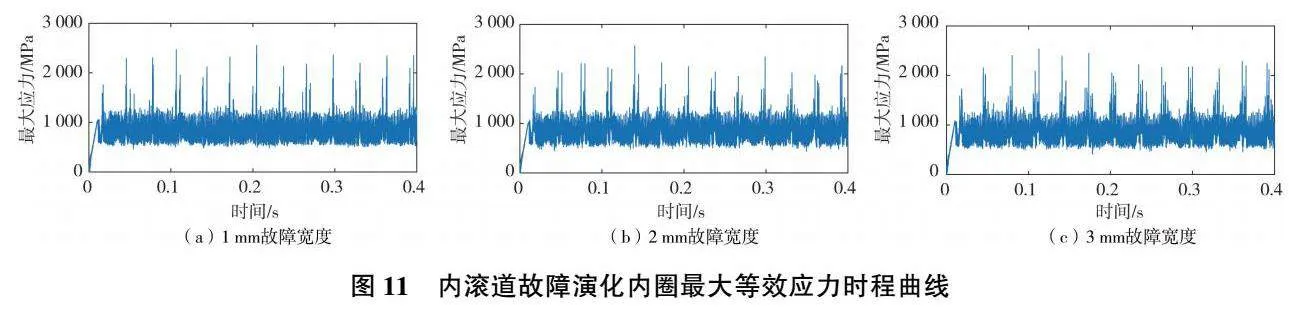
在內滾道故障演化情況下，各故障寬度下內圈最大應力時程曲線如圖11所示。

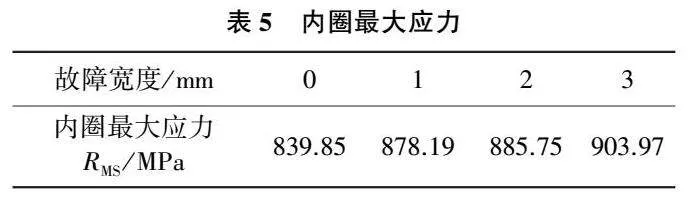
從圖11中可以發現，在內滾道存在故障時，內圈承受的最大等效應力同樣存在明顯的周期性。但是相比于外滾道故障情況，在內滾道故障情況下，在每個轉動周期內，由于故障位置在持續旋轉，故障前后邊緣與滾動體的接觸相比外滾道情況更加復雜。不同故障寬度下最大應力的RMS值如表5所示。

從表5中可以看出，在故障沿著內滾道演化時，內圈承受的應力有明顯的增強。同時對比表3可以發現，在無故障情況下以及相同故障尺寸下，內圈的應力水平均大于外圈。

4結語

本文以NU202型圓柱滾子軸承為研究對象，通過ANSYS/LS-DYNA建立其外滾道、內滾道故障演化的有限元模型，基于仿真分析得出如下結論：

1）仿真計算得出的故障特征頻率與理論解之間的誤差小于1%，該模型能夠準確地模擬軸承滾道故障狀態；

2）在外滾道及內滾道故障的演化過程中，軸承振動響應升高，但特征頻率成分不會改變，故障所在套圈的應力水平均有顯著升高；

3）在相同的故障尺寸下，故障位于內滾道時會引發更強烈的振動響應，同時內圈的應力水平大于外圈。

參考文獻：

［1］ 楊國安. 滾動軸承故障診斷實用技術［M］. 北京：中國石化出版社，2012：10-11.

［2］ SHAHA D R ，KULKARNI S S. Vibration analysis of deep groove ball bearing using finite element analysis［J］. International Journal of Engineering Research and Applications， 2015，5（5）：44-50.

［3］ 楊子臻，左彥飛，邵化金，等. 基于顯式有限元的轉子不平衡與軸承故障耦合分析［J］. 軸承，2021（2）：8-13，16.

［4］ SINGH S，KPKE U G，HOWARD C Q，et al. Analyses of contact forces and vibration response for a defective rolling element bearing using an explicit dynamics finite element model［J］. Journal of Sound Vibration，2014，333（21）：5356-5377.

［5］ SINGH S，HOWARD C Q，HANSEN C H，et al. Analytical validation of an explicit finite element model of a rolling element bearing with a localised line spall［J］. Journal of Sound and Vibration，2018，416：94-110.

收稿日期：20230330

第一作者簡介：任悅（1997—），女，遼寧沈陽人，碩士研究生，研究方向為滾動軸承的動力學建模，renyue@nuaa.edu.cn。

DOI：10.19344/j.cnki.issn1671-5276.2024.06.023