預應力筋應力松弛模型數值算法研究

摘" 要：針對預應力結構中預應力筋應力松弛效應的精確計算問題，基于fib 2010《歐洲混凝土結構規范》給出的預應力筋應力與時間的松弛關系，推導表征預應力筋應力松弛的率型本構模型，并構建該本構模型的數值迭代算法，在ABAQUS的UMAT二次開發平臺上編寫該模型的數值求解程序。分別針對無黏結預應力結構和有黏結預應力結構2種情況，對程序的正確性和適用性進行了驗證。研究表明編寫的計算程序可實現預應力結構中應力松弛效應的準確模擬，提出的應力松弛模型的程序開發思路也適用于ANSYS、ADINA等有限元軟件。

關鍵詞：預應力結構；應力松弛；本構模型；數值算法；二次開發

中圖分類號：TU501 文獻標志碼：A 文章編號：2095-2945（2025）04-0021-04

Abstract： Aiming to address the precise calculation issue of stress relaxation effect in prestressed structures， a rate-type constitutive model was developed based on the relaxation relationship between stress and time as outlined in the fib 2010 European Code for Concrete Structures. This model characterizes stress relaxation of prestressed reinforcement under varying strain conditions， and a numerical iteration algorithm was formulated for this constitutive model. Anumerical solution program for this model was developed using the UMAT secondary development platform of ABAQUS. The accuracy and applicability of the program were validated for both unbonded prestressed structures and bonded prestressed structures. Research has demonstrated that the program accurately simulates the stress relaxation effect in prestressed structures. Moreover， the proposed program development approach for stress relaxation models is also suitable for finite element software such as ANSYS and ADINA.

Keywords： prestressed structure; stress relaxation; constitutive model; numerical algorithm; secondary development

預應力筋張拉后，在長度不變的情況下應力隨時間增長而不斷降低的現象稱為應力松弛[1]，應力松弛是導致預應力結構發生預應力損失的重要原因。對于核電廠預應力混凝土安全殼、LNG儲罐、大跨度預應力混凝土橋梁結構、張拉機械臂等結構[2-4]，預應力損失是導致結構出現受力問題的主要原因。相關研究表明，帕勞的K-B大橋倒塌即與混凝土主梁中預應力損失過大有關[5]。針對預應力結構中的應力松弛問題，眾多學者進行了試驗和理論研究，得到了豐富的研究成果[6-9]。

預應力混凝土結構中應力松弛會導致結構中儲備的壓應力減少，進而影響混凝土徐變；混凝土收縮徐變發生后又會影響應力松弛，二者存在耦合關系。然而我國規范僅給出了應力松弛引起的最終預應力損失值的計算方法，無法準確反映應力松弛與混凝土收縮徐變間的耦合效應。對于重要的預應力混凝土結構，如安全殼，在評估其結構服役性能時，需要精確考慮混凝土收縮徐變與預應力筋應力松弛間的關系，此時需要采用時步分析方法[10]，將計算分為若干時間步驟，每個時間步內可以計算混凝土收縮徐變和應力松弛，實現二者關系的動態變化，最終得到考慮相互影響的總體預應力損失。

本文基于fib 2010《歐洲混凝土結構規范》（以下簡稱fib 2010規范）給出的預應力筋應力與時間的松弛關系，推導了表征預應力筋應力松弛的率型本構模型，構建了可實現該本構模型時步分析的數值迭代算法，在ABAQUS的UMAT二次開發平臺上編寫了求解程序，并對程序的準確性和適用性進行了驗證。

1" 基本理論

1.1" 控制方程

我國GB 50010—2010《混凝土結構設計規范》僅給出預應力筋應力松弛導致的最終損失值，表達式類似于式（1）（普通松弛鋼絞線松弛計算公式），由于沒有給出應力松弛導致的預應力損失與時間的關系，不能直接用于構建時步分析方法。fib 2010規范給出了應力松弛與時間的關系式，本文以fib 2010規范給出的應力松弛表達式為例，進行數值迭代算法構建

σl4=0.4-0.5σcon ， （1）

式中：σl4為應力松弛引起的預應力損失；σcon為預應力張拉控制力；fptk為預應力筋極限強度標準值。

fib 2010規范給出的應力松弛表達式為

=σ1 ， （2）

式中：σ0為初始預應力；σv（t）為t時刻的預應力；σ1、？姿1和k均為常數，與鋼筋種類及施加的應力水平有關。

式（2）是應力與時間的關系，需要轉換成材料應力與應變的關系，將式（2）對時間求導

=-ρ1λktk-1 ， （3）

式中：將應力σ0表達為應變的函數：F（ε0），本構方程中不能顯含時間，從式（2）中求出時間t的表達式，代入式（3）得

根據金屬黏塑性理論[5]：dt內松弛應力增量dσ可以通過將初始值假定為當前應變ε且保持不變，即可以用當前應變ε替換式（4）中的ε0，于是式（4）變為

實際結構中預應力筋受外部荷載影響，其應變是不斷變化的，對于一個微量加載過程（Δε，Δσ），可以將其分解：首先保持應變不變，產生某個應力增量，而后跟隨一個突然增大/減小應變增量，最終的綜合效果為（Δε，Δσ）。該過程的數學表達如下。

給定應變增量dε，材料中的應力增量分為2項，即彈性應力增量和松弛應力增量

dσ=dσe+dσv ， （6）

其中，dσe=Et dε，Et為鋼束彈性模量，將式（5）代入上式，得

式（7）即為表征應力松弛的率型本構模型，當為常應變時，上式左端為0，即回到式（5）。

1.2" 數值算法

在時間步[tk，tk＋１]范圍內對式（7）進行積分可得

。（8）

采用隱式歐拉格式對式（8）進行離散

式中：Δσk=σk+1-σk，εk+1=εk+Δεk。

有限元中采用位移法求解時，上一步計算結果和這一步中輸入的應變增量是已知的，因此，式（9）是一個關于Δσk的代數方程，可采用數值方法進行求解，進而可得到應力增量Δσk，從而求得預應力松弛應力的時步分析結果。編程計算時，鋼束彈模的取值需要根據鋼束應力狀態，判斷其是否屈服，若進入塑性階段，需要根據應變狀態計算鋼束屈服后的彈模。

2" 程序實現

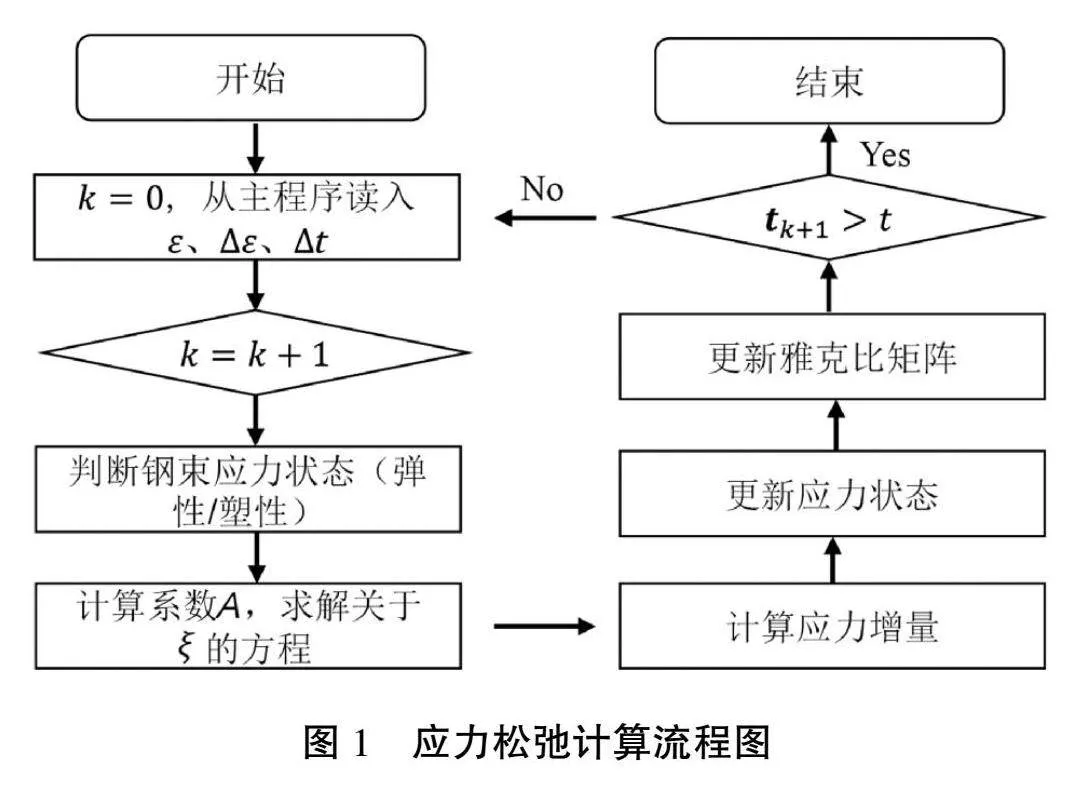
有限元軟件ABAQUS提供了材料子程序（UMAT）模塊，用戶可通過UMAT編寫自定義材料本構關系，供主程序調用。UMAT本質處理單元應力和應變狀態的轉化，在UMAT程序計算之前會從ABAQUS主程序調用上一步迭代完成后的計算結果。對于松弛程序，主要是調用上一步的應變；然后根據本步計算中的應變增量和時間步增量，通過UMAT計算應力增量，從而更新主程序中的應力狀態和雅克比矩陣，重復這個過程，即可實現隨時間變化的松弛應力計算。根據上述推導過程，本文在ABAQUS的UMAT材料子程序二次開發平臺上編寫了應力松弛的計算程序，UMAT算法流程圖如圖1所示。

3" 算例

3.1" 單獨鋼束

為驗證程序的正確性，本文首先對單獨預應力鋼束進行驗證，單獨鋼束的應力松弛具有解析解，對應于實際結構中的無黏結預應力筋，如安全殼結構中的灌油鋼束、鋼混組合結構中的體外預應力筋，此時鋼束僅兩端受約束。

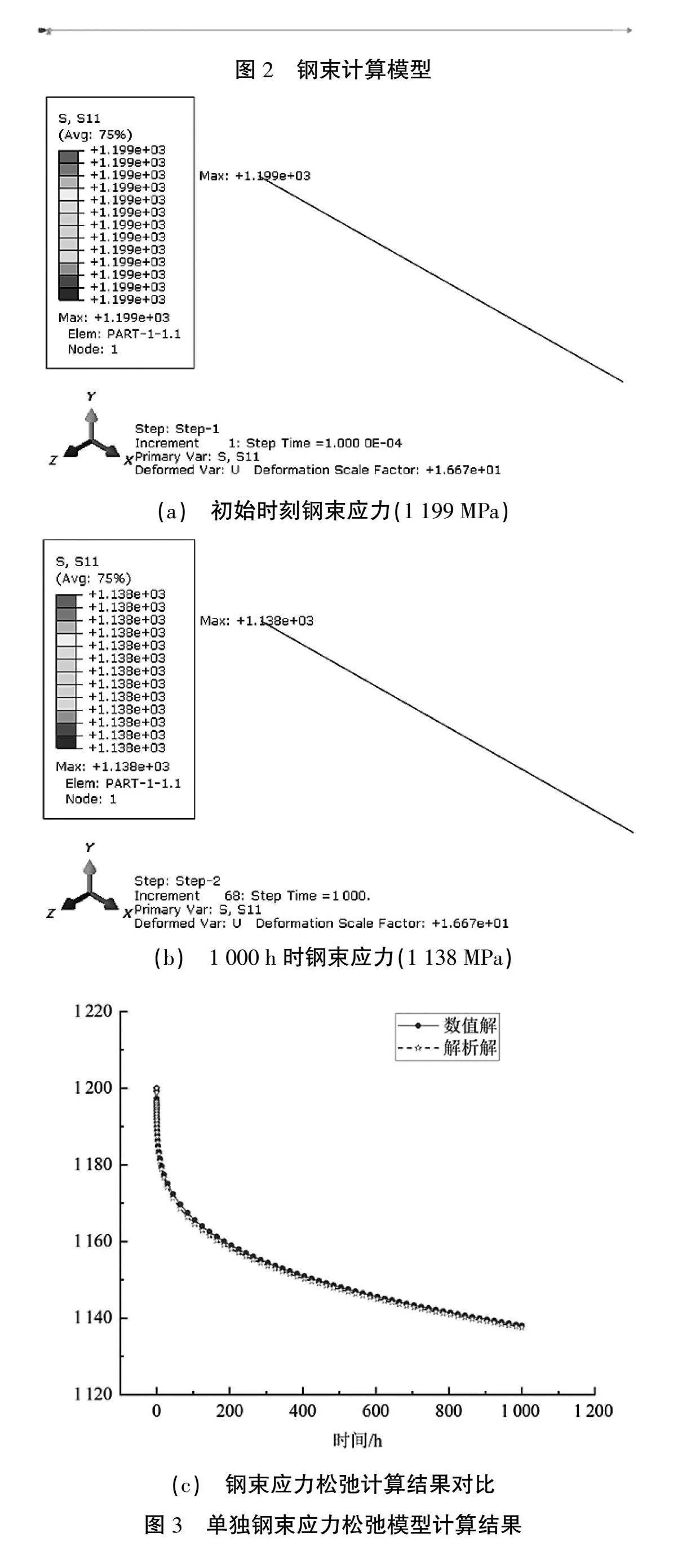
采用ABAQUS建立了單根鋼束的有限元計算模型，算例中鋼束長1 m，一端采用固定邊界條件，另一端施加6 mm位移荷載，模擬張拉，計算采用的參數見表1，計算模型如圖2所示，計算結果如圖3所示。采用本文程序計算的應力松弛結果與解析解的最大相對誤差為0.1%，表明了本文程序的正確性。

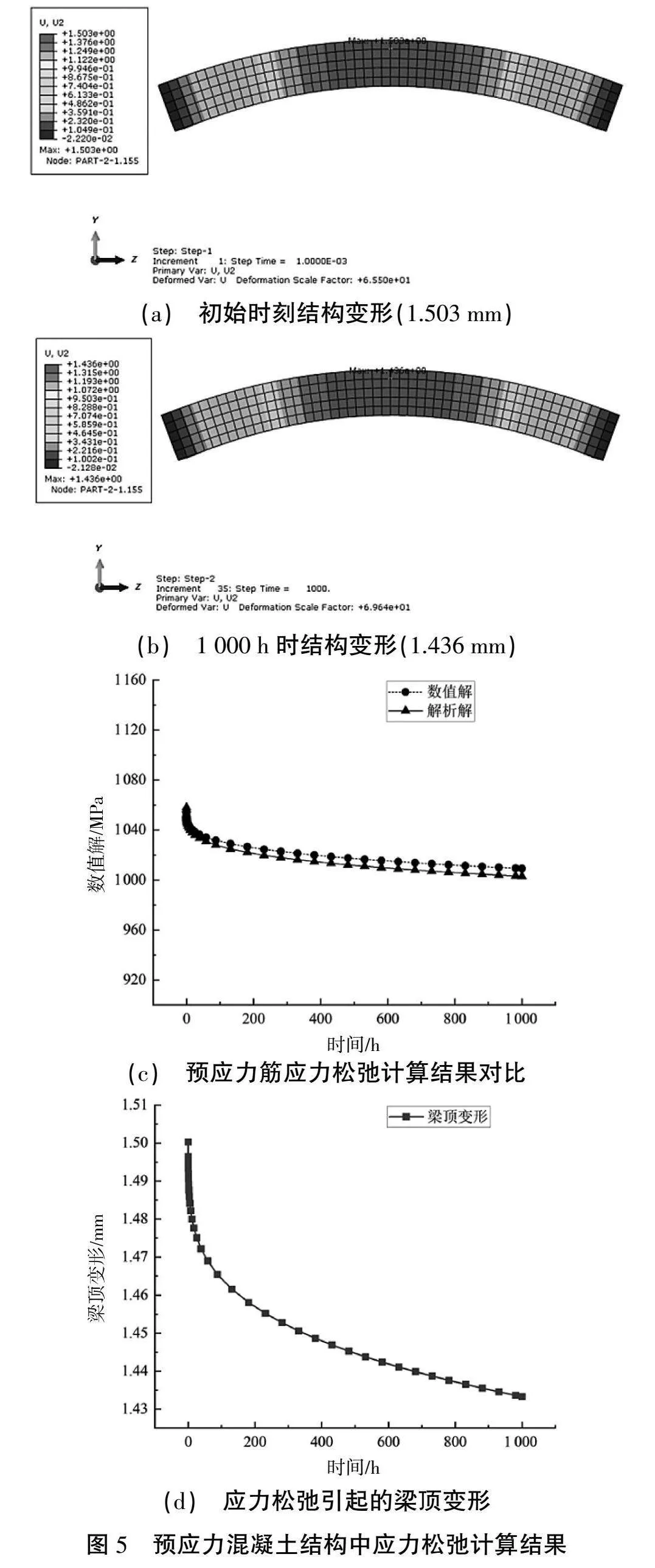
3.2" 預應力混凝土結構

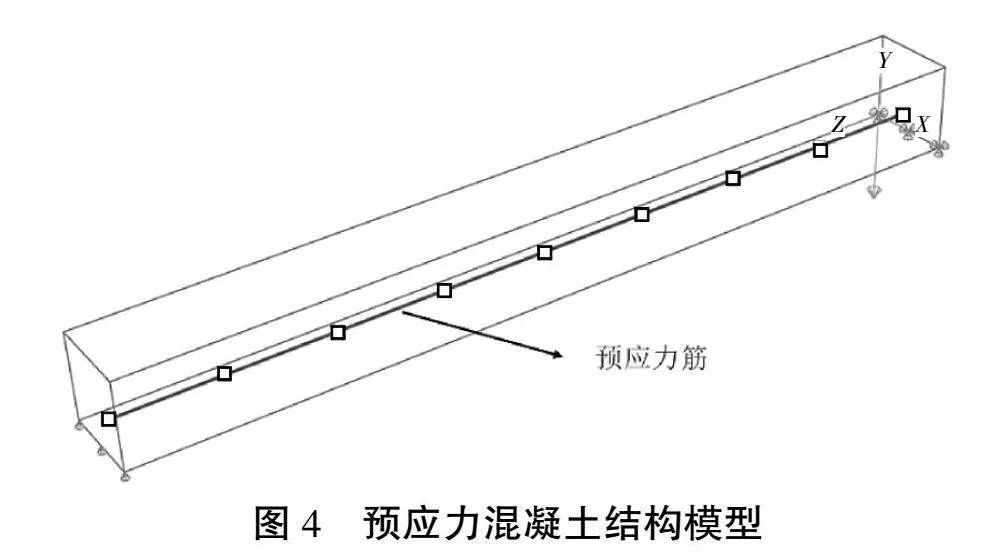
為進一步驗證有黏結預應力混凝土結構中本程序的適用性，建立一預應力混凝土梁，該梁長1 m，截面尺寸為0.1 m×0.1 m，采用簡支邊界條件；鋼束布置在距底緣0.025 m處，鋼束截面積為130 mm2，混凝土彈模為33 500 MPa；鋼束初張力為1 056 MPa，采用降溫方式施加；混凝土采用C3D8實體單元，鋼束采用T3D2桁架單元，通過節點位移協調將鋼束與混凝土耦合在一起以模擬實際結構中灌漿后的效果。整個結構承受預應力和自重作用，模型如圖4所示，計算結果如圖5所示。計算表明，自重和預應力作用下梁發生上拱變形，隨著應力松弛出現，梁的起拱逐漸變小；程序計算的鋼束松弛應力與解析解的最大相對誤差為0.6%，表明本文程序適用于預應力混凝土結構應力松弛效應分析。

4" 結論

1）本文基于ABAQUS二次開發平臺編寫的預應力筋應力松弛迭代算法可實現單獨鋼束應力松弛和預應力混凝土結構中應力松弛效應的精確分析。

2）本文提出的應力松弛模型的程序開發思路也適用于ANSYS、ADINA等有限元軟件。

參考文獻：

[1] ZDENK P. BAANT M J. Creep and Hygrothermal Effects in Concrete Structures[M]. Dordrecht： Netherland： Springer， 2018.

[2] 程旭東，王子棟，馬川，等.大型LNG儲罐外罐長期預應力損失分析[J].天然氣工業.2018，38（11）：97-105.

[3] 葛藝芃，姜超，張亮，等.考慮預應力松弛的張拉整體機械臂可靠性分析[J].工程力學，2023，41（10）：237-246.

[4] 周勇政.瀝青基灌漿料灌漿引起的結構預應力損失研究[J].中國鐵道科學.2019，40（3）：15-23.

[5] BAANT Z P， YU Q. Relaxation of Prestressing Steel at Varying Strain and Temperature： Viscoplastic Constitutive Relation[J]. Journal of engineering mechanics. 2013，139（7）：814-823.

[6] 曾濱，許慶，徐曼.1 860 MPa鋼絲疲勞松弛交互作用性能試驗研究[J].工業建筑，2019，49（11）：159-162，168.

[7] 王國富，李強，路林海，等.錨索預應力蠕變損失計算新模型及工程應用[J].建筑結構，2018，48（15）：110-114.

[8] 王宇威，潘鉆峰，曾濱，等.疲勞荷載作用對預應力長期損失影響試驗研究與理論分析[J].工程力學，2023（41）：1.

[9] 曾濱，徐曼，許慶.預應力筋/索非線性疲勞-松弛應力理論模型與計算方法[J].土木工程學報，2022，55（9）：1-8.

[10] 潘立本，陳蓓.用分段逼近法計算混凝土收縮與徐變引起的構件預應力損失[J].工程力學，1998（4）：123-126.