基于減法優化的凹凸山地無線傳感器網絡定位算法

摘 要：針對傳統的三維無線傳感器網絡節點定位算法在計算復雜地形坐標時因地形環境影響而出現無解的問題，提出一種基于減法優化的凹凸山地無線傳感器網絡定位算法。首先，將復雜多峰模型投影降維成二維模型，并引入基于隨機變量的帳篷混沌映射對減法優化初始粒子進行混沌映射，增強初始粒子的多樣性及均勻性；然后，采用黃金正弦對粒子的位置進行更新，使其跳出局部最優解；最后，使用Levy飛行策略模擬在搜索空間中的隨機探索，使算法有更好的全局搜索能力。實驗結果表明，該算法相較于其他傳統算法，具有更好的穩定性和更高的定位精度，使用該算法對山地地形中未知節點的坐標進行計算，能夠有效降低計算誤差。

關鍵詞：無線傳感器網絡；多跳定位；減法優化；多峰模型；帳篷混沌映射；黃金正弦；Levy飛行策略

中圖分類號：TP393 文獻標識碼：A 文章編號：2095-1302（2025）05-000-06

0 引 言

無線傳感器網絡（Wireless Sensor Network， WSN）是由眾多微型傳感器節點構建的網絡體系，主要用于實時監測和收集環境中的各種參數信息。WSN在環境監測、農業、醫療、交通等多個領域都展現出巨大的應用潛力[1-2]。在WSN應用中，將感知數據與位置信息結合至關重要。缺乏位置信息的數據通常難以發揮其實用價值，因此節點定位成為WSN中的一個關鍵問題[3]。

WSN定位可以根據不同情況主要分為測距定位與非測距定位兩種類別，而非測距定位中的三維DV-HOP算法由于具備方法簡單、定位精度較高、對復雜地形的定位過程中具有良好的適用性等優點，一度成為學者研究的熱點。文獻[4]在復雜山地環境中，依據節點的稀疏程度，應用三維近似三角形內點測試（APIT）算法和DV-HOP算法預估未知節點的位置，以搜索未知節點的鄰近節點，形成平面結構。隨后，通過向這些平面作垂線，并穿過未知節點的坐標，得到一系列垂直坐標。最終，取這些垂點坐標的平均值，作為未知節點的精確位。這種方法結合了兩種算法的優勢，提高了在復雜地形中節點定位的準確性和可靠性，但未考慮到計算的復雜度問題。文獻[5]通過合并多個通信半徑，減小跳數帶來的誤差。然后，計算錨節點的平均跳躍距離，設置跳躍閾值，剔除誤差較大的錨節點。最后，采用粒子群優化算法代替極大似然估計方法，得到優化后的多通信半徑跳距校正。但該算法后期容易陷入局部最優。文獻[6]通過用距離加權因子和距離相似鏈路法，分別改善跳數和跳距的誤差，進而提高了算法的性能。然后，采用蝴蝶搜索算法和自適應的局部搜索策略，優化未知節點的位置尋優過程。這些改進措施使得算法在穩定性上更為出色，同時在定位精度上也達到了更高的水平。然而，這也增加了通信成本。文獻[7]有效地利用了山區地形環境的特點，采用局部平面擬合方法，對山區地形表面進行建模。該算法巧妙地將原本復雜的三維空間定位運算轉化為更為簡潔的二維平面的定位運算，有效提高了節點的定位精度。文獻[8]利用無人機與無線傳感器網絡中協作傳感器節點間的測量模型來構造黎曼流形，并通過推導流形上的梯度，確定迭代中最快的下降方向，從而推導出協同無人機節點幾何構型對應的GDOP，并將其用于調整迭代下降速率，使算法快速收斂，具有良好的精度。但是該方法的精度提升有限。文獻[9]首先利用3DDV-HOP算法計算節點的初始位置，隨后將初始位置用投影的方法投影至山頭地形表面，進行精確的位置矯正。雖然定位精度有所提升，但在不同環境下的精度提升并不明顯。

上述算法中，雖然針對復雜環境的定位做了一定的改進，但還是存在許多不足之處，而且沒有考慮當應用環境相對較小時，定位算法無解的問題。對此，本文提出一種基于減法優化的凹凸山地無線傳感器網絡定位算法（MWL-SA）。首先，通過投影降維的方法，將復雜的三維復雜山地降維成二維等高線平面；其次為了解決最小二乘法在求解位置坐標時容易出現的無解問題，通過引入隨機變量的帳篷混沌映射對減法優化初始粒子進行混沌映射，增強了初始粒子的多樣性及均勻性；其次，采用黃金正弦算法對粒子的位置進行更新，使其跳出局部最優解；然后，使用Levy飛行策略模擬在搜索空間中的隨機探索，避免算法陷入局部最優解，讓其更好地探索全局搜索空間；最后，用改進后的減法優化算法在凹凸地形中對每個未知節點位置進行計算，有效地解決了定位算法無解的問題，并且降低了待定位節點位置的計算誤差。

1 投影法降維

垂直投影是一種基于幾何學原理的定位方法，用于通過已知節點的位置信息推斷未知節點的位置坐標。具體而言，垂直投影方法基于已知節點之間的距離測量，通過在水平平面上建立虛擬二維網格進行節點位置的估計。垂直投影方法的具體步驟如下：

（1）距離測量和節點位置確定：通過距離測量技術（如距離測量、信號強度測量等），獲取已知節點之間的距離信息，同時確定已知節點的位置坐標。

（2）建立虛擬二維網格：在水平平面上建立一個虛擬二維網格，將已知節點的位置映射到網格中。

（3）垂直投影：對于未知節點，通過將其與已知節點進行垂直投影，將已知節點在水平平面上的位置與距離關系推廣到未知節點，從而推斷未知節點的位置。

2 減法優化算法

減法優化算法（Subtraction-Average-Based Optimizer， SABO）的設計理念來自數學概念，如平均值、搜索代理位置的差異以及目標函數的兩個值的差異符號[10]。該算法的具體步驟如下：

（1）算法初始化

3 融合黃金正弦的減法優化算法（GSABO）

（1）基于隨機變量的帳篷混沌映射

由于SABO存在隨機性大的缺點，決定引入有序統一的帳篷映射來改進它。許多學者已經應用帳篷映射來解決優化問題[11]。然而，帳篷映射并不穩定。為了降低這種不穩定性帶來的影響，研究者們采用了基于隨機變量的帳篷映射，取得了良好的效果[12]。因此，本文引入了基于隨機變量的帳篷映射策略來改進SABO的初始化，使總體初始化更加有序，增強了算法的可控性。其具體公式如式（5）所示：

（3）黃金正弦策略

黃金正弦算法（Golden Sine Algorithm， Gold-SA）[13]是一種旨在優化位置更新方式的算法。該算法基于黃金分割比例與正弦函數的特性進行設計。由于原始SABO算法并沒有在每次迭代時利用全局最優解，而是利用所有粒子的位置做減法平均值來達到更新的目的，因此，當初始粒子位置不好的時候，極其容易陷入局部最優解，所以引入黃金正弦算法對粒子位置進行更新。這樣既不會過多地增加適應度值的計算量，也可以利用黃金正弦算法在全局尋優的優勢幫助SABO算法跳出局部最優解。其位置更新數學表達式如下：

通過融入Levy飛行策略， SABO算法全局搜索能力得到了顯著增強，同時其收斂速度也更為迅捷。這使得該算法在處理高維問題和非線性問題時展現出前所未有的高效性，并具備強大的魯棒性和適應性，為優化問題提供了有效的解決方案。

4 MWL-SA定位算法

4.1 建立多峰地形模型

圖1（a）所示為實際多峰地形圖。首先，建立起伏地勢下的多峰地形方程。通過對多峰地形的仔細觀察與分析以及對三維多峰曲面函數進行仿真，發現二者之間有很好的擬合性，所以采用三維多峰曲面函數作為多峰地形的數學模型，并在多峰地形上隨機布放傳感器節點，如圖1（b）所示。

4.2 獲得未知節點到錨節點的最小跳數

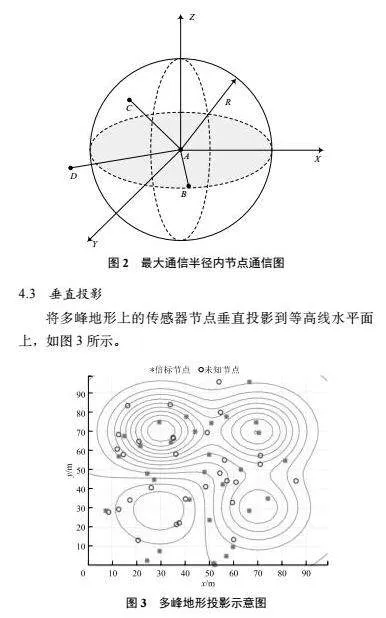
采用DV-HOP 定位算法計算跳數。但是考慮到該算法的特性，如果用其原始算法計算跳數會導致計算出的定位坐標有很大的誤差，所以采用多通信半徑的方式來降低跳數誤差。如圖2所示，錨節點A與未知節點B、C、D之間的距離都被視為1跳。這將導致AB、AC、AD之間的距離誤差較高。因此，設定錨節點有多種通信半徑，分別為R、0.75R、0.5R和0.25R。在錨節點廣播自身信息時， B、C、D節點到錨節點A的最小跳數分別設置為1/4、1/2、3/4。在通信半徑R內，節點接收到節點發來的信息時進行轉發。每個節點會獲得它們之間的最小跳數，這種方法使得跳距計算更準確。

4.3 垂直投影

將多峰地形上的傳感器節點垂直投影到等高線水平面上，如圖3所示。

從圖3中可以看出，整個多峰地形由左、中、右山峰以及一處低洼組成。左邊的山峰比中間以及右邊的山峰高，從每個等高線之間的距離來看，左邊的山峰坡度高于右邊山峰，比中間的山峰坡度略高，且坡度遠遠大于其下方的低洼。由此可得，從左邊山峰到低洼，其坡度依次遞減。又因為無線傳感器節點隨機分布在整個多峰地形中，且山峰上節點居多，使得定位難度大大增加。

4.4 計算未知節點坐標

在求解多峰地形中無線傳感器網絡節點定位的問題時，最小二乘法作為一種常用的數學工具，經常遇到無解的問題。這主要是由于多峰地形的復雜性和非線性特性，使得最小二乘法在嘗試擬合節點位置與信號強度之間的關系時，難以找到一個滿足所有條件的解。具體來說，山地地形的起伏、山谷、山峰等特征會導致信號傳播受到多種因素的影響，如多徑效應、陰影效應等，這使得信號強度與節點位置之間的關系變得復雜且難以準確描述。在這種情況下，最小二乘法可能無法找到一組合適的參數來準確反映這種關系，從而導致無解的問題。此外，當傳感器節點分布不均或數量不足時，最小二乘法也可能因為數據稀疏或信息不足而無法得出有效的解。因此，在解決多峰地形中的無線傳感器網絡節點定位問題時，需要尋求更為靈活和有效的方法來克服最小二乘法可能出現的無解問題。本文提出GSABO算法，將最小二乘求解問題轉換成優化算法迭代問題，很好地解決了最小二乘法無解的問題，且提高了山地環境的定位精度。

5 仿真實驗與結果分析

5.1 GSABO算法優化性能分析

為了驗證GSABO算法的優化性能，本文選取了4個標準測試函數，這些函數各自具有不同的特點，能夠全面考察算法的尋優能力，具體函數特性見表1。

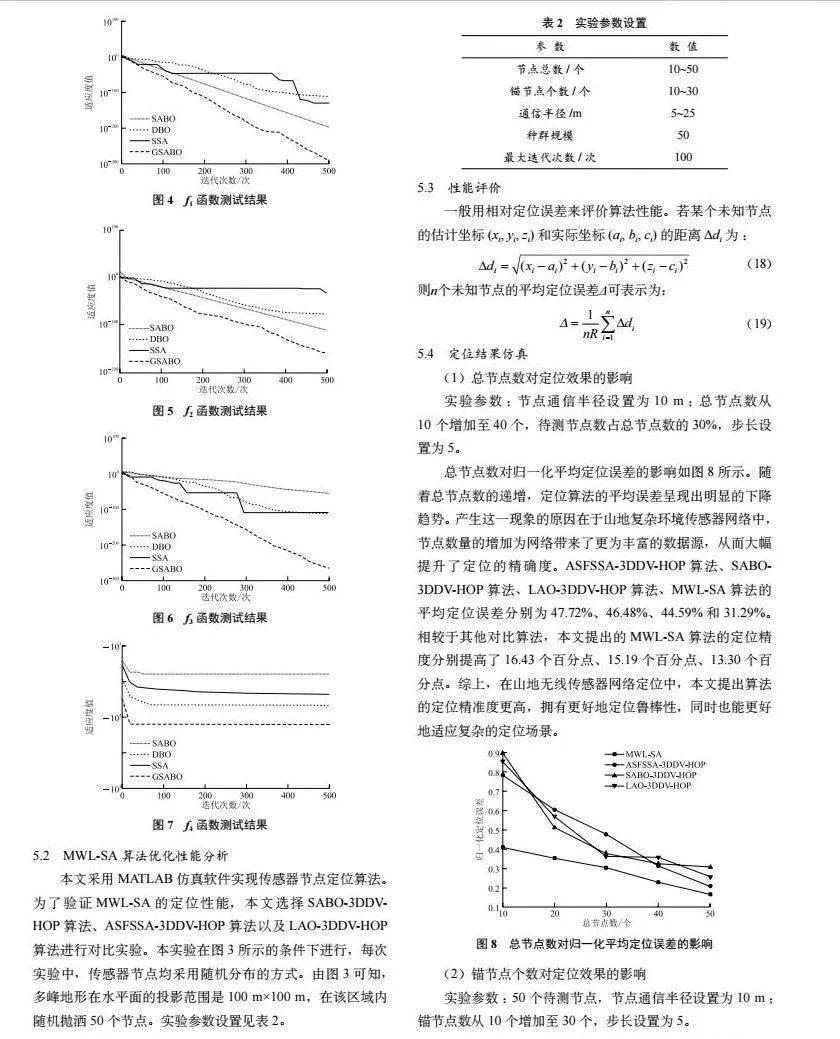
本文選擇標準減法算法（SABO）、蜣螂算法（DBO）、麻雀算法（SSA）作為對比算法進行實驗。所有算法都在MATLAB軟件中進行仿真。將實驗中算法的相關參數設置為：種群數量30個、最大迭代次數500次。本文對每個測試函數進行了30次獨立運行，并對實驗結果進行統計。具體測試結果如圖4～圖7所示。

由圖4可知，本文所提出的算法展現了最快的收斂速度，這充分證明了在f1函數下，本文算法的尋優能力更出色，且其重復精度相較于其他算法更高。進一步觀察圖5、圖6和圖7可知，對于函數f2 ～ f4，結果與f1相似，本文算法的尋優性能仍是最佳。值得注意的是，本文算法所獲得的適應度值最小，其尋優得到的平均適應度值更加接近理論最優值0，這充分展示了其卓越的優化性能。

5.2 MWL-SA算法優化性能分析

本文采用MATLAB仿真軟件實現傳感器節點定位算法。為了驗證MWL-SA的定位性能，本文選擇SABO-3DDV-HOP算法、ASFSSA-3DDV-HOP算法以及LAO-3DDV-HOP算法進行對比實驗。本實驗在圖3所示的條件下進行，每次實驗中，傳感器節點均采用隨機分布的方式。由圖3可知，多峰地形在水平面的投影范圍是100 m×100 m，在該區域內隨機拋灑50個節點。實驗參數設置見表2。

5.3 性能評價

一般用相對定位誤差來評價算法性能。若某個未知節點的估計坐標（xi， yi， zi）和實際坐標（ai， bi， ci）的距離Δdi為：

5.4 定位結果仿真

（1）總節點數對定位效果的影響

實驗參數：節點通信半徑設置為10 m；總節點數從10個增加至40個，待測節點數占總節點數的30%，步長設置為5。

總節點數對歸一化平均定位誤差的影響如圖8所示。隨著總節點數的遞增，定位算法的平均誤差呈現出明顯的下降趨勢。產生這一現象的原因在于山地復雜環境傳感器網絡中，節點數量的增加為網絡帶來了更為豐富的數據源，從而大幅提升了定位的精確度。ASFSSA-3DDV-HOP算法、SABO-3DDV-HOP算法、LAO-3DDV-HOP算法、MWL-SA算法的平均定位誤差分別為47.72%、46.48%、44.59%和31.29%。相較于其他對比算法，本文提出的MWL-SA算法的定位精度分別提高了16.43個百分點、15.19個百分點、13.30個百分點。綜上，在山地無線傳感器網絡定位中，本文提出算法的定位精準度更高，擁有更好地定位魯棒性，同時也能更好地適應復雜的定位場景。

（2）錨節點個數對定位效果的影響

實驗參數：50個待測節點，節點通信半徑設置為10 m；錨節點數從10個增加至30個，步長設置為5。

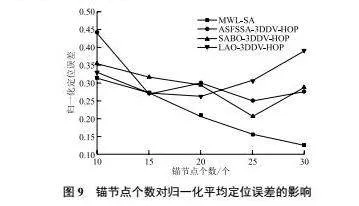
錨節點個數對歸一化平均定位誤差的影響如圖9所示。隨著錨節點數量的增加，歸一化定位誤差逐漸降低。這一現象的產生主要歸因于錨節點數量的不足。在錨節點數量較少時，由于提供的定位信息有限，導致定位誤差相對較大，從而顯著增加了精確確定目標位置的難度。因此，錨節點的數量在確定定位精度方面起到了至關重要的作用。通過有效增加錨節點的數量，定位系統能夠利用更多錨節點的距離和信號強度信息，進行深入的綜合分析。這使得定位系統能夠進行更為準確的定位計算，從而顯著提升定位精度。ASFSSA-3DDV-HOP算法、SABO-3DDV-HOP算法、LAO-3DDV-HOP算法、MWL-SA算法的平均定位誤差分別為30.80%、29.23%、31.29%、 21.54%。與其他定位算法相比，本文提出的MWL-SA算法在定位精度上有了顯著提升，分別提高了9.26個百分點、7.69個百分點和9.75個百分點。這一結果充分證明了增加錨節點數量以及采用有效的定位算法對于提高定位精度的積極作用。

（3）通信半徑對定位效果的影響

實驗參數：總節點數固定為50個，待測節點數固定為30，節點通信半徑設置為5～25 m，步長設置為5。

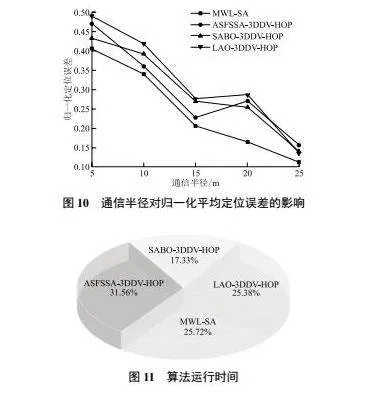
通信半徑對歸一化平均定位誤差的影響如圖10所示。通信半徑的大小在很大程度上影響著歸一化平均誤差的大小。主要是由于通信半徑的增大加強了節點間的信息交流與互動。當節點間的通信更為頻繁和深入時，定位系統便能收集到更多、更全面的定位數據，從而能夠更為精確地確定每個節點的位置。這種信息交互的增強，有效降低了定位過程中的誤差，提高了定位精度。ASFSSA-3DDV-HOP算法、SABO-3DDV-HOP算法、LAO-3DDV-HOP算法、MWL-SA算法的平均定位誤差分別為29.78%、 29.83%、32.17%、24.63%。與其他算法相比，本文所提的MWL-SA算法的定位精度分別提高了5.15個百分點、5.20個百分點、7.54個百分點。再次證明了在通信半徑增大后，通過優化節點間的信息交互，能夠有效提高定位精度，減小定位誤差。

（4）計算開銷分析

實驗設定在同一環境下，對四種算法的運行時間進行對比分析，如圖11所示。

由圖11的數據可知，MWL-SA算法運行時間較高于SABO-3DDV-HOP算法，略高于LAO-3DDV-HOP算法，但其平均定位誤差又明顯降低。ASFSSA-3DDV-HOP算法不僅運行時間長且定位誤差大。綜上，本文所提的MWL-SA算法雖然計算時間略長，但其定位精度顯著提高。

6 結 語

本文針對三維起伏地形中無線傳感器網絡節點定位的挑戰，提出了一種基于減法優化的凹凸山地無線傳感器網絡定位算法。該算法綜合運用了投影降維、混沌映射、黃金正弦算法及Levy飛行策略等技術手段，顯著提升了算法在復雜地形中的定位精度和穩定性。相較于傳統DV-HOP算法，本文算法在性能上表現出明顯的優勢。本文算法通過優化節點定位策略，減小了節點之間的定位誤差，提高了整個網絡的定位精度和穩定性。此外，本文算法還具有較強的適應性，能夠應對不同類型的地形和環境，可以為無線傳感器網絡在火山監測、空間探索等領域的應用提供了有力支持。未來，將進一步深入研究該算法在實際場景中的應用，探索其在更廣泛領域的潛在價值和適用性，推動無線傳感器網絡技術的發展和應用。

注：本文通訊作者為彭鐸。

參考文獻

[1]李振，馮鋒.基于Halton序列WOA-GWO算法的WSN覆蓋研究[J].物聯網技術，2024，14（2）：43-47.

[2] LOKESH D， REDDY N V U. Optimizing the power consumption in WSN through target tracking [C]// 2021 Fifth International Conference on I-SMAC （IoT in Social， Mobile， Analytics and Cloud）.Palladam， India： [s.n.]， 2021： 1334-1338.

[3]余修武，穆靜，劉永.基于遺傳模擬退火優化的DV-HOP定位算法[J].華中科技大學學報（自然科學版），2024，52（3）：149-155.

[4]郝占軍，閆燕，黨小超.面向復雜山地環境的WSN節點三維定位算法[J].計算機工程，2019，45（6）：146-151.

[5] WU Y， ZHANG C， TONG L， et al. Location optimization based on improved 3D DV-HOP algorithm in wireless sensor networks [J]. IEEE access， 2023， 11： 85525-85536.

[6]王磊，崔嵩，牛婷婷.復雜環境下多策略改進麻雀搜索的定位算法[J].小型微型計算機系統，2024，45（11）：2768-2776.

[7]胡中棟，王俊嶺，王振東，等.山區復雜地形的無線傳感器網絡節點定位算法[J].北京郵電大學學報，2019，42（5）：113-118.

[8] SONG Z， ZHANG Y， YU Y， et al. Cooperative positioning algorithm based on manifold gradient filteringin UAV-WSN [J]. IEEE sensors journal， 2024， 24（8）： 12676-12688.

[9]胡中棟，肖華為. 適應山頭地形的無線傳感器網絡節點定位算法[J]. 計算機工程與應用，2016，52（10）：104-107.

[10] TROJOVSK P， DEHGHANI M. Subtraction-average-based optimizer： a new swarm-inspired metaheuristic algorithm for solving optimization problems [J]. Biomimetics， 2023， 8（2）： 149.

[11] LI Y， HAN M， GUO Q. Modified whale optimization algorithm based on tent chaotic mapping and its application in structural optimization [J]. KSCE journal of civil engineering， 2020， 24（12）： 3703-3713.

[12] OUYANG C， QIU Y， ZHU D. Adaptive spiral flying sparrow search algorithm[J]. Scientific programming， 2021.

[13]王寧，何慶. 融合黃金正弦與 sigmoid 連續化的海鷗優化算法[J].計算機應用研究，2022，39（1）：157-162.

[14]彭鐸，劉明碩，謝堃.擴展卡爾曼濾波的改進蛇定位算法在WSN中的應用[J].無線電工程，2024，54（6）：1489-1496.